
This blog has a modern version at http://blog.tanyakhovanova.com/, where you can leave comments. This page contains the copies of 88 blog entries for years 2007 and 2008. The latest essays are at http://www.tanyakhovanova.com/MathBlog.html
My initial plan was to apply for academic jobs this December. I didn't do it. Here are my reasons:
That's why my next step must be to persuade a university or a college that they need a professor of recreational mathematics. It is obvious that such positions are needed. Recreational mathematics is the only existing field of mathematics that is very popular, but not represented in math departments. After all, recreational mathematics is very important in popularizing mathematics, in bridging the gap between the advanced research and common folks. Recreational mathematics is vital in energizing American math education in general.
Hey, are you a math faculty member? If you agree with me, talk to your Head of Department about this idea, especially if you live in the Boston area. Then give me a call.
If you remember, in my previous essay My Paper Road to Academia, my big plan was to write lots of academic papers. So far I have written eight papers this year (seven of them are uploaded to the arxiv). I also have ideas and partial results for 19 more papers, but I have stopped writing them. Here is the story of My Paper Road Block.
I started sending my papers to different places, where they were rejected. Then I was invited to the Gathering for Gardner. Participants are allowed to publish their paper in the proceedings of the conference, but we have to pay for it. So this publication really felt more like adding insult to injury than a lucky break.
Finally I realized that I can put three lucky letters — M, I, and T — on my papers. I don't remember if I told you that I am currently holding a visiting scholar position at MIT.
I continued sending my papers out without receiving any positive response. As a result of these rejections and the long waiting periods to receive an answer, my writing process slowed down until it halted.
To my delight, a month ago I received letters of acceptance for three papers, almost simultaneously. Here is the tally so far for my eight papers:
The funny part is that on all the accepted papers I was affiliated with MIT, and on all the rejected papers I was not.
To be fair, I have to admit that there might be another explanation. All the accepted papers were sent out later in time. Perhaps I'm getting better at choosing the right journals.
Because of inertia, I'm still not writing papers. On the positive side, I have more time to write for this blog, and it is much more rewarding. Sometimes I reject my own essays. Sometimes I send them to myself for revision. But I judge my pieces on quality, not on my affiliation.

My knowledge about vampires comes mostly from the two TV series Buffy The Vampire Slayer and Angel. If you saw these series you would know that vampires can't stand the sun. Therefore, they can't get any tan at all and should be very pale. Angel doesn't look pale but I never saw him going to a tanning spa. Nor did I ever see him taking vitamin D, as he should if he's avoiding the sun.
But this is not why I'm confused about vampires. My biggest concerns are about vampires that are numbers.
Vampire numbers were invented by Clifford A. Pickover, who said:
If we are to believe best-selling novelist Anne Rice, vampires resemble humans in many respects, but live secret lives hidden among the rest of us mortals. Consider a numerical metaphor for vampires. I call numbers like 2187 vampire numbers because they're formed when two progenitor numbers 27 and 81 are multiplied together (27 * 81 = 2187). Note that the vampire, 2187, contains the same digits as both parents, except that these digits are subtly hidden, scrambled in some fashion.
Some people call the parents of a vampire number fangs. Why would anyone call their parents fangs? I guess some parents are good at blood sucking and because they have all the power, they make the lives of their children a misery. So which name shall we use: parents or fangs?
Why should parents have the same number of digits? Maybe it's a gesture of gender equality. But there is no mathematical reason to be politically correct, that is, for parents to have the same number of digits. For example, 126 is 61 times 2 and thus is the product of two numbers made from its digits. Pickover calls 126 a pseudovampire. So a pseudovampire with asymmetrical fangs, is a disfigured vampire, one whose fangs have a different number of digits. Have you ever seen fangs with digits?
In the first book where vampires appeared Keys to Infinity the vampire numbers are called true vampire numbers as opposed to pseudovampire numbers.
We can add a zero at the end of a pseudovampire to get another pseudovampire, a trivial if obvious observation. To keep the parents equal, we can add two zeroes at the end of a vampire to get another vampire. Adding zeroes is not a very intellectual operation, but a vampire that can't be created by adding zeroes to another vampire is more basic and, thus, more interesting. In the book Wonders of Numbers: Adventures in Mathematics, Mind, and Meaning a vampire where one of the multiplicands doesn't have trailing zeroes is called a true vampire, as opposed to just a vampire. Thus, the trueness of vampires changes from book to book, adding some more confusion. It looks like the second definition of a true vampire is more widely adopted, so I will stick to it.
By analogy, we should call pseudovampires that do not end in zeroes, true pseudovampires. It's interesting to note that by adding zeroes we can get a true vampire from any pseudovampire that is not a vampire. You see how easy it is to build equality? Just add zeroes.
A true vampire might not be true as a pseudovampire. For example, a vampire number 1260 = 20 * 61 is generated by adding a zero to a pseudovampire 126 = 2 * 61. In this case, the pseudovampire is truer than the vampire. Why does something more basic get a prefix "pseudo"?
Here's another question. Why do vampires have to have two fangs? Can a vampire have three fangs? For example, 11439 = 9 * 31 * 41. This generalization of vampires should be called mutant vampires. Or multi-gender vampires.
To create more confusion, a mutant vampire can, at the same time, be a simple vampire: 1395 = 31 * 9 * 5 = 15 * 93.
Of course, nothing prevents a mutant vampire from being politically correct, that is, to have multiple and equal parents with the same number of digits, as in 197925 = 29 * 75 * 91.
People continue creating a mess with vampires. For example, a definition of a prime vampire number is floating around the Internet. When you look at this name, your first reaction is that a prime vampire is a prime number. But a vampire is never prime as it is always a product of numbers. By definition a prime vampire is a vampire with prime multiplicands, for example 124483 = 281 * 443. So "prime vampire number" is a very bad name. We should call these vampires prime-fanged vampires — this would be much more straightforward.
To eliminate some of this confusion, we mathematicians should go back and rename vampires consistently. But in the meantime, check out the illustration of vampire numbers shown above that I found at flickr.com with this description:
Like the count von Count in Sesame Street, there is a tradition that vampires suffer terribly from arithromania: the compulsion to count things. To keep vampires from wreaking murderous havoc at night, poppy seeds were strewn about their resting places. On waking, the vampire would be compelled to count the seeds. It would take him all night, and keep him from mischief.
It is unfortunate that crooks understand probability. Here is a scam that was very popular back in Russia.
A bad guy pretends that he has a close relative on the hiring committee of a college. He takes bribes from prospective students, promising to help them pass the entrance exams at this college. He doesn't guarantee the admission, but he guarantees the money back. After getting the money, he does nothing. If the student passes the entrance exams, he keeps the money. If not, he returns the money. Simple probability — someone will pass the exams by chance, making him a lot of money.
Here is another Russian scam. This time the crooks have some understanding of conditional probability. These "psychics" promise to correctly predict the gender of your future child. They tell you a random gender, but for their bookkeeping they file the opposite gender. This way, even if you complain, they still keep your money. They show you their books and pressure you into believing that you misunderstood, misheard or misremembered the answer. The probability that you complain if they are right is zero.
Let us all learn probability theory to recognize scams and not fall for them.
China Girls Math Olympiad is becoming an international math Olympiad for girls. When I first heard about this competition I felt very sad. I need to explain myself here.
For many years I felt very proud that math Olympiads do not separate the genders. Most Olympic sports, like running or swimming, have separate competitions for men and women. I felt that joint competitions for math demonstrated the spirit of equality in our math community. I felt that insofar as gender didn't matter, mathematics was more democratic than other sports.
At the same time I do understand how people might assume for the following reasons that a math competition among only girls would be useful:
See also the article: First US Team to Compete in the China Girls Mathematical Olympiad.
On the other hand, this development scares me. If we have a separate girls Olympiad, will that soon lead us to have two Olympiads, one for boys and one for girls? Two separate Olympiads would be a defeat for women mathematicians. Or, maybe I shouldn't be scared. The percentage of girls at the most prestigious mathematics competition, the International Mathematical Olympiad, is so small that it can be viewed as virtually boys-only.
Mathematics is becoming similar to chess. There is a World Chess Championship where both men and women are allowed to compete, and there is a separate Women's World Chess Championship. The interesting part is that Judith Polgar, by far the strongest female chess player in history, never competed in the Women's World Chess Championship. I suspect that I understand Judith. She probably feels that women-only competitions diminish her, or that chess is about chess, not about gender. In any case, I hope that one day the separate girls Olympiad will not be needed.
Browsing Braingle I stumbled upon a standard probability puzzle which is very often misunderstood:
Suppose I flip two coins without letting you see the outcome, and I tell you that at least one of the coins came up heads. What is the probability that the other coin is also heads?
The standard "wrong" answer is 1/2. Supposedly, the right answer is 1/3. Here is the explanation for that "right" answer:
For two coins there are four equally probable outcomes: HH, HT, TH and TT. Obviously, TT is excluded in this case, and of the remaining three possibilities only one has two heads.
Here is the problem with this problem. Suppose I flip two coins without letting you see the outcome. If I get one head and one tail, what will I tell you? I can tell you that at least one of the coins came up heads. Or, I can tell you that at least one of the coins came up tails. The fact that I can tell you different things changes the a posteriori probabilities.
You need to base your calculation not only on your knowledge that there are only three possibilities for the outcome: HH, HT and TH, but also on the conditional probabilities of these outcomes, given what I told you. I claim that the initial problem is undefined and the answer depends on what I decide to say in each different case.
Let us consider the first of two strategies I might use:
I flip two coins. If I get two heads, I tell you that I have at least one head. If I get two tails I tell you that I have at least one tail. If I get one head and one tail, then I will tell you one of the above with equal probability.
Given that I told you that I have at least one head, what is the probability that I have two heads? I leave it to my readers to calculate it.
Suppose I follow the other strategy:
I flip two coins. If I get two tails, I say, "Oops. It didn't work." Otherwise, I say that I have at least one head.
Given that I told you that I have at least one head, what is the probability that I have two heads? If you calculate answers for both strategies correctly, you will have two different answers. That means the problem is not well-defined in the first place.
Teacher: Why didn't you do your statistics homework?
Student: I read a statistical study that the students who spend more time on their homework get lower grades.
Teacher: So you didn't do your homework in order to increase your grades?
Student: Yep.
Teacher: I have been teaching you that correlation doesn't mean causality. Did it ever occur to you that students with good grades already know some of the material and they do not need much time to complete their homework?
Student: Oh?
Teacher: You are getting an F for not doing your homework. Now you might understand causality better.
When I came to the US, I heard about Mensa — the high IQ society. My IQ had never been tested, so I was curious. I was told that there was a special IQ test for non-English speakers and that my fresh immigrant status and lack of English knowledge was not a problem. I signed up.
There were two tests. One test had many rows of small pictures, and I had to choose the odd one out in each row. That was awful. The test was English-free, but it wasn't culture-free. I couldn't identify some of the pictures at all. We didn't have such things in Russia. I remember staring at a row of tools that could as easily have been from a kitchen utensil drawer as from a garage tool box. I didn't have a clue what they were.
But the biggest problem was that the idea of crossing the odd object out seems very strange to me in general. What is the odd object out in this list?
Cow, hen, pig, sheep.
The standard answer is supposed to be hen, as it is the only bird. But that is not the only possible correct answer. For example, pig is the only one whose meat is not kosher. And, look, sheep has five letters while the rest have three.
Thus creative people get fewer points. That means, IQ tests actually measure how standard and narrow your mind is.
The second test asked me to continue patterns. Each page had a three-by-three square of geometric objects. The bottom right corner square, however, was empty. I had to decide how to continue the pattern already established by the other eight squares by choosing from a set of objects they provided.
This test is similar to continuing a sequence. How would you continue the sequence 1,2,3,4,5,6,7,8,9? The online database of integer sequences has 1479 different sequences containing this pattern. The next number might be:
Usually when you are asked to continue a pattern the assumption is that you are supposed to choose the simplest way. But sometimes it is difficult to decide what the testers think the simplest way is. Can you replace the question mark with a number in the following sequence: 31, ?, 31, 30, 31, 30, 31, … You might say that the answer is 30 as the numbers alternate; or, you might say that the answer is 28 as these are the days of the month.
Towards the end of my IQ test, the patterns were becoming more and more complicated. I could have supplied several ways to continue the pattern, but my problem was that I wasn't sure which one was considered the simplest.
When I received my results, I barely made it to Mensa. I am glad that I am a member of the society of people who value their brains. But it bugs me that I might not have been creative enough to fail their test.

I am looking forward to the 2009 Women and Math program at Princeton. The irony is that I lived in Princeton for seven years and the only time I visited this program was for the lecture course on wavelets by Ingrid Daubechies.
I felt that mathematics should be genderless and pure; that the only basis for a program should be mathematics itself. I tried to ignore the problems of women mathematicians by pretending they didn't exist. By the time I realized that I might very well love to hang out with a large group of female mathematicians, I left Princeton.
Can you imagine how glad I was when I got a call inviting me to join the organizing committee for the Women and Mathematics Program last year? I was so eager that I arranged a math party at the Program and gave my own talk about Topology in Art.
What can I tell you? I loved the program. For the first time in my life I didn't feel like a loner, but rather that I belonged to a group. I also felt envious, because when I was a student we didn't have anything like this in Russia.
I am going to be on the program this year too. The subject is Geometric PDE. I am so looking forward to it that I'm already planning another math party.
Once I was at a party and a woman was complaining that her car insurance bills were enormous. Her expensive car was hit three times while it was parked. She was whining about how unfair it was for her to be paying increased insurance premiums when it hadn't been her fault. I didn't tell her my opinion then, but I'm going to write about it now.
Though such things can happen, it is possible to reduce the probability of your parked car being hit.
In my personal experience the most frequent parking accident happens when someone backs out of a driveway and there is a car parked in a space which is usually empty. People often back out of their driveways on autopilot. If you park on a narrow street with no other cars — a sign that people don't usually park there, do not park across from a driveway or close to a driveway.
There are many other common sense ideas. Don't park at a corner. Choose the better lit areas. Don't park next to a truck or a van, because they might not see you very well and if they hit you, they'll do more damage. Don't park next to an old, battered car because they have less to lose than you do. New cars are the best neighbors. Not only are owners of new cars usually more careful, but new cars are also often leased. And people who lease a car are even more careful, because they have to return it in good order.
When you are choosing a perpendicular parking spot, here's a cute idea. Pick cars with four doors as your neighbors. Cars with two doors have bigger doors and if you are too close, they might scratch you.
Here's what I would have told that woman: If your car has been hit so many times while parked, you should rethink your parking strategy.
Browsing the Internet, I stumbled upon a coin puzzle which I slightly shrank to emphasize my point:
Carl flipped two coins and was asked if at least one of the two coins landed "heads up". He replied, "Yes. In fact the first coin I flipped landed heads up." What is the chance that Carl's coins both landed heads up?
The standard answer is 1/2, because there are only two possibilities for the coin flips: HH and HT. But how do we know that these possibilities are equally probable?
The answer depends on what we expect Carl to say when he flips two heads. My personal assumption is that Carl is a perfectionist and always volunteers extra information. If Carl gets two heads, I would expect him to say, "Yes. In fact both coins I flipped landed heads up." In this case the answer to the puzzle is 0.
Another strange but reasonable assumption is that upon flipping two heads, there is an equal probability that Carl would say either, "Yes. In fact the first coin I flipped landed heads up;" or, "Yes. In fact the second coin I flipped landed heads up." In this case, the answer to the puzzle is 1/3.
I could describe an assumption for Carl's answering strategy that leads to the puzzle's answer of 1/2, but it looks too artificial to me.
This puzzle is not well-defined, but unfortunately there are many versions of it floating around the Internet with incorrect solutions.

One day I got a phone call from Victor Gutenmacher, one of the members of the jury for the USSR Math Olympiad. At that time I was 15 and had won two gold medals at the Soviet Math Olympics. Victor asked me about my math education. I explained to him that although I went to a special school for gifted children, I wasn't doing anything else. In his opinion, other kids were using more advanced mathematics for their proofs than I was. He said I was coloring everything in black and white; other kids were using calculus, while I was only using elementary math. He asked me if I would like to learn more sophisticated mathematics.
I said, "Sure." After considering several different options, Victor suggested Israel Gelfand's seminar at Moscow State University. He told me that this seminar might suit me because it starts slowly, picking up pace only at the end. He also told me that the seminar was like a theater. Little did I know that I would become a part of this theater for many years to come. I also didn't know that I would meet my third husband, Joseph Bernstein, at this seminar. Joseph used to sit in the front row, and I watched his back at the seminar for more years than I later spent together with him.
The next Monday evening, I went to the seminar for the first time. Afterwards, Gelfand approached me and asked me if I had an academic adviser. I said, "No." He asked me how old I was. I said, "Fifteen." He told me that I was too old and that I had to choose an adviser without delay. I said, "But I do not know anyone and, besides, I need some time to think about it." He replied, "I'll give you two minutes."
I paced the halls of the 14th floor of the Moscow State University for a couple of minutes, pretending to think. But really, I didn't know about any other options. He was the only math adviser I had ever met. So I came back and asked Gelfand, "Will you be my adviser?"
He agreed and remained my adviser until I got my PhD 14 years later.
When you talk over the phone with an adult stranger, you can generally determine if this person is male or female. From this, I conclude that the voice characteristics are often noticeably different for males and females. There are many other characteristics that have a different distribution by gender — for example, height.
My question is: "Can we find a trait such that the distributions are the same for both genders?"
Trying to find the answer, I remembered what we learned in high school about the genetics of eye color. I checked the Internet on the subject and discovered that the story is somewhat more complicated than what I studied 30 years ago, but still we can say that eye color is defined by several genes, which are located on non-sex chromosomes. That means, your eye color depends on the genes your parents have and doesn't depend on your sex. A boy and a girl from the same parents have the same chances for any particular eye color.
Since eye coloring has nothing to do with gender, women and men are equal in the eyes of eye colors.
Does that mean that if we check the distribution of eye color for the world population, the distribution histogram will be the same for men and women? That sounds like a logical conclusion, right? I would argue that this is not necessarily the case.
Let me remind you that the distribution of eye color depends on the country. China has an unprecedented gender imbalance, with 6% more men than women in its population. As the eye color of Chinese people is mostly dark brown, this creates an extra pool for a randomly chosen man in the world to have a darker eye color than for a randomly chosen woman. If we exclude China from consideration, we can still have different distributions. For example, in Russia the life expectancy for women is 15 years longer than the life expectancy for men. Consequently, Russia has 14% less men than women, while globally the male/female sex ratio is 1.01. Therefore, eye colors common in Russia will contribute to female eye colors more than those of male.
What if we consider only one country? Let us look at the US. Immigrants to the US are mostly males. If the distribution of eye color for immigrants is different than the distribution for non-immigrants, then male immigrants contribute more to the eye color distribution than female immigrants.
There are so many factors impacting eye color distribution, that it isn't clear whether it's possible to find a group of people other than siblings in which the distribution of eye color would be the same for women and men.
We see that eye color distribution, which theoretically doesn't depend on gender, when measured in a large population can produce different distributions for men and women.
Recently I wrote a theoretical essay titled "Math Career Predictor", where I assumed that the distribution of math ability is different for men and women. In reality, there is no good way to measure math ability, hence we do not have enough data to draw a complete picture. For the purposes of this discussion let us assume that we can measure the math ability and that Nature is fair and gave girls and boys the same math ability. My example with eye color shows that if we start measuring we might still see different distributions in math ability in boys and girls.
My conclusion is that if we measure some ability and the distribution is different for boys and girls, or for any other groups for that matter, we can't just conclude that boys and girls are different in that ability. For some distributions, like voice, we probably can prove that the difference is significant, but for other characteristics, different distribution graphs are not enough; we need to understand the bigger picture before drawing conclusions.
I got a funny book for a gift called Plato and a Platypus Walk into a Bar…: Understanding Philosophy Through Jokes. I couldn't stop reading it. This book is an overview, and thus not very deep, but I enjoyed being reminded of philosophical concepts I've long since forgotten. Besides, I collect math jokes and many philosophical jokes qualify as mathy ones.
For example, self-referencing jokes:
Relativity — this term means different things to different people.
I especially liked jokes related to logic:
If a man tries to fail and succeeds, which did he do?
I knew most of the jokes, but here's a math joke I never heard before:
Salesman: "Ma'am, this vacuum cleaner will cut your work in half."
Customer: "Terrific! Give me two of them."
Here is a standard logic puzzle:
A criminal is sentenced to death. He is allowed to make one last statement. If the statement is true, the criminal will be sent to the electric chair. It the statement is false, he will be hanged. Can you suggest a good piece of advice for this man?
I can offer many pieces of advice to this man. The simplest thing is to keep silent. Or he can communicate without making statements, like asking, "Can I have some crème brûlée, please?"
One can argue that the puzzle implies that it's a favor to allow the prisoner to make a last statement, but without it he will die anyway. In this case the standard piece of advice to this man would be to create a paradoxical situation by saying, "I will be hanged."
Another, less standard, idea is to state something that is very difficult to check. For example, to give the exact number of planets in our galaxy, or posit that P = NP. My son, Sergei, suggested saying that "Schrödinger's cat is dead."
But the most popular idea among my AMSA students is to say, "I am sorry." I'm not 100% sure that they mean it as a statement that is impossible to check. Maybe they think that these words can do magic and save lives. Or maybe it could be the best thing for a criminal to say before dying.
My scientific adviser Israel Gelfand was one of the greatest mathematicians in Russia. His seminar was famous.
One of the unique features Gelfand invented for his seminar was a role for a seminar participant that he called a designated listener (kontrol'nyy slushatel' in Russian). I played this role for four years.
This is how it works. The speaker starts his lecture and Gelfand interrupts him. He then turns to me and asks if I understand what the speaker just said. If I say "no," he says that I am a fool. If I say "yes", he invites me to the blackboard to explain. Usually, Gelfand finds some fault in my explanation and calls me a fool anyway. As a result, whatever I do, I end up as a fool.
Ironically, I admired Gelfand for the way he conducted his seminars. I went to so many seminars where it was clear that no one understood anything. He was the only professor I knew who made sure that at least one person at his seminar — himself — understood everything.
The problem was that he convinced me that I really was a fool. I dreaded Mondays and I considered quitting mathematics. The situation changed when I started dating Andrey, my future second husband. He made a strong effort to convince me that I was not a fool; rather, Gelfand was a bully. I understood what Andrey was saying, but I wasn't able to take it to heart. Not that I trusted my supervisor more than my lover, but I was more willing to believe that something was wrong with me than with someone else.
Andrey's hard work wasn't in vain. One fine day Professor G. from Western Europe was invited to give a talk at Gelfand's seminar. During his talk Gelfand interrupted him many times, told him that he wasn't a good lecturer, and that his results were neither interesting nor meaningful. After several hours of torture Professor G. became tearful. At that moment it hit me that Andrey was right. I am thankful to Professor G. for his tears; they opened my eyes.
The next step for Andrey was to convince me to resist Gelfand. His idea was for me to tell Gelfand, the next time he asked me if I understood: "Go f**k yourself!" (I mean the Russian equivalent).
At that time, I had never pronounced the f-word, even in my own head. But I didn't have any other ideas. So I started preparing myself to do this. Finally one day I was ready. Gelfand interrupted the speaker and turned towards me as if he were about to ask me to be the designated listener. I looked back at him. He paused, looked at me again, and turned around. He never asked me to be the designated listener again.
— Do you love tomatoes?
— Eating them — yes; otherwise not so much.
The word "love" expresses an emotion. But the range of emotion it can span is an enormous interval between a slight preference and a burning desire.
— Do you love tomatoes?
— I love tomatoes so much that I eat them with ketchup.
Still we can usually figure out the intensity of this emotion from the context. When someone says that he loves M.C.Escher, nobody concludes that he is a necrophiliac.
I do feel lucky that there is a special variation of the word "love" reserved to express passion. When I say that I am in love, everyone understands that I am talking about a man. You can't say, "I am in love with my stick-shift car." Or, maybe, you can; but I am stepping into the territory of dirty jokes:
— Anyone know any? I have lots of tomatoes, but they're all green. A dirty joke or two might make them blush.
Why am I writing this? I do not even like tomatoes. Maybe it is because yesterday I bought some prunes and they reminded me of the tomato who went out with a prune, because he couldn't find a date.
Anyone knows that sometimes the text is not exactly what it seems to be. There are many different simple ways to hide a secret message inside your text. So, your humble blogger decided to run an experiment. How should we go about it? I decided to hide a secret message inside this short essay. Do you see it? Do you notice that my text is artificially adjusted for some extra purpose? Everyone can feel that this text sounds different than my usual postings. Nothing should stop you from solving this puzzle now.
In this essay I would like to explain why I am not yet a professor of mathematics.
Today at 49 I am still in search of my dream job. My gender is not the main reason that I don't have an academic position or another job I like. My biggest problem is myself. My low self-esteem and my over-emotional reactions in the past were the things that most affected my career.
I remember how I came to Israel Gelfand's seminar in Moscow when I was 15. He told me that I was too old to start serious mathematics, but that he would give me a chance. He said that at first I might not understand a thing at his seminar, but that every good student of his comes to understand everything in a year and a half. The year and a half passed and I wasn't even close to understanding everything. Because of this I was devastated for a long time.
I had always had problems with my self-esteem and being a student of Gelfand just added to them. My emotional reactions, while they impacted my work in mathematics, were not exclusively related to mathematics. When my second divorce started, not only did I drop my research, I quit functioning in many other capacities for two years.
I was extremely shy in my early teenage years. By working with myself, I overcame it. When I moved to the US, my shyness came back in a strange way. I was fine with Russians, but behaved like my teenage self with Americans. For two years of my NSF postdoc at MIT, I never initiated a conversation with a non-Russian.
For the second time I overcame my shyness. Now, if you met me in person, you wouldn't believe that I was ever shy.
I became much happier in the US, than I ever was in Russia, but still my emotions were interfering with my research. Because it was so difficult to find an academic job here, I felt tremendous pressure every time I sat down with a piece of paper to work on my research. My mind would start flying around in panic at the thought that I wouldn't find a job, instead of thinking about quantum groups.
Over all, I think that my inability to control my emotions, together with my low self-esteem, might have impacted my career much more than the fact that I am a woman, per se. Being a mathematician is not easy; being a female mathematician is even more difficult. Still, in my own life, I know I can only blame myself.
The good news is that I have changed a lot, after many years of self-repair. This is why I have made the risky decision, at the age of 49, to try to get back to academia. And this time I have a great supporter — my new self.
Notation is very important in your mathematical papers. Here are the most famous rules on how mathematicians use notation.
Do not explain your notation. Do not waste your time explaining your notation. Most of them are standard anyway. Your paper will look more impressive if you plunge right into your statements. So a good paper can start like this:
Obviously, p is never divisible by 6 …
Everyone knows that p is a prime number.
Use a variety of alphabets. This way you demonstrate your superior education, while expanding your notation possibilities. Not to mention that it looks so pretty:
sin2ℵ + cos2ℵ = 1.
You also get points for drawing a parallel between alpha and alef.
Denote different things with the same letter. It is very important to maintain continuity with the papers in your references, so you should use their notation. Besides, some notation is standard:
Suppose S is an ordered set. Elements of the permutation group S act on this set: for any s in S, sS is the corresponding action.
Mathematicians secretly compete with each other. The goal is to denote as many different things as possible with the same letter in one paper. My personal record was to denote six different things with the letter G. There are two versions of this competition to maximize the number of different meanings of one letter: it can be done either on the same page or in the same formula.
Use different notation for the same thing. The ultimate achievement would be to change your notation in the middle of your sentence:
Gauss showed that the sum of integers between 0 and k inclusive is equal to n(n+1)/2.
Replace standard notation with your own. Your paper will look much more complex than it is. Besides, if someone adopts your notation, they'll have to name it after you:
Let us use the symbol ¥ for denoting an integral.
Denote a constant with a letter. Letters look more serious than numbers. You will impress your colleagues.
We will be studying graphs in which vertices are colored in only three colors: blue, red and green. For simplicity the number of colors is denoted by k.
As a bonus, when you prove your theorem for three colors, you can confuse everyone into thinking that you proved it for any number of colors.
Do not specify constraints or limits. When you use a summation or a integral, the limits look so bulky that they distract from your real formula. Besides, it's time-consuming and too complicated for most text editors. Look at this perfect simplicity:
∑ i2 = n(n+1)(2n+1)/6.
Everyone knows that you are summing the integers between 1 and n inclusive. Oops. It could be between 0 and n. But 02 = 0 anyway, so who cares?
Be creative. You can mix up these rules or invent your own.
Let us consider a triangle with N sides. Actually, it is better to replace N by H, because in Russian the letter that looks like English H is pronounced like English N. Let us denote the base of the triangle by X. By the way, that is the Russian letter that is usually pronounced like the English letter H, so sometimes I will interchange them. The height of the triangle is, as always, denoted by H.
By following these simple rules, you will earn great respect from your readers.
This story happened at a colloquium that was conducted during the Women and Math program at Princeton last year. The room was full of women waiting for the colloquium to start. A young man appeared at the door. He looked around in complete surprise. I watched the fear fade from his face when he must have decided that he had the wrong room. He disappeared, but reappeared at the door very soon. He had obviously checked the schedule and had realized that, in fact, he had come to the right room in the first place. His face started changing colors. He was terrified. A few minutes later, he left.
I sat there thinking: women have to deal with this type of situation every week. He could afford to skip just one lecture, but if a girl wants to do math she has to be courageous almost every seminar. I mentally applauded the girls around me for being that courageous.
Wait a minute! I am a woman myself. I went to seminars where I was the only girl hundreds of times. How did I feel? Actually I think my mind never registered that I was the only girl. I never cared. The first time I really thought that the gender of people in a room might be an issue was during that colloquium last year.
I started wondering why it had never bothered me. Could it be that the Soviets did a good job of teaching me not to pay attention to people's gender? Could be. But wondering back in time, I remembered something else too.
When I was a child I wasn't a girly girl. I was not interested in dolls; I preferred cars. I didn't play house or doctor; I played war. To tell the whole truth, I actually did have a doll that I loved, but I never played with it. I liked having it. The doll was a gift from my father's second wife and it was way beyond my mother's price range. I think I had an admiration for the quality and the beauty of this toy.
So, while appreciating the courage that the other girls might have needed to do math, I was sitting there pondering my own indifference to the gender of people at seminars and my relative comfort with large groups of men. But this comfort had its own price. I felt comfortable with the group I wasn't a part of, while I felt different from the group I was a part of. My price of being comfortable at math seminars was loneliness.
I've got this puzzle from Nick Petry.
Captain Flint is dying. All his treasures are buried far away. He only has 99 pieces of gold with him. Filled with remorse at the last moments of his life, he decides that he only wants to take one piece of gold with him to his grave. The rest of the gold he will give to the families of two men that he had killed the day before.
Though Captain Flint is heavily drunk he notices that no matter which piece he takes for himself, he can divide the leftover 98 pieces into two piles of 49 pieces each of the same weight. Prove that all the gold pieces are of the same weight.
For an additional challenge, Sasha Shapovalov suggested the following generalization of the previous puzzle.
Captain Flint has N gold pieces and yesterday he killed not two but K men. He wants to take one piece with him to his grave and to divide the rest into equi-weighted piles, not necessarily of the same number of pieces. If he can choose any piece to take with him and is able to divide the rest, prove that N – 1 is divisible by K.
Both of these puzzles can be easily solved if the weight of every gold piece is an integer or even a rational number. If you don't assume that the weights are rational numbers, then I do not know an elementary solution, but I do know a simple and beautiful solution using linear algebra for both puzzles.
Even pirates need linear algebra to divide their treasure. Hooray for linear algebra!
To translate from a Russian joke, borrowing money is taking someone else's: temporary; giving back your own: forever.
This is a story about my great-uncle Fred. His name is not Fred, of course, because I don't want to reveal which one of my thirteen great-uncles created this ingenious scheme.
My great-uncle Fred asked to borrow 100 rubles from my mother. He was notorious for not returning money, but he knew how to work my mother. He whined about being sick and urgently needing to buy pills, until my mother, who has a big heart and is an easy touch, gave up. Of course, Fred wasn't in a hurry to return the money. But 100 rubles was a lot of money for my mother and she wasn't planning on giving up trying to get it back. My mother started bugging her uncle with increased intensity. Finally Fred promised to return the money as a gift for mom's upcoming birthday.
Of course, it was tacky to present the money he owed as a gift, but my mom was so glad that she would finally get her money back, that she was actually looking forward to it.
During her party, as the guests sat around the table, Fred got up to give the birthday toast. Then Fred handed my mother an envelope and said, "Congratulations on your birthday! Here is a gift for you." Everyone applauded.
My mom felt that something in this scene was not quite right. Why was the applause so enthusiastic when he was just returning a debt? After the party my mother decided to investigate. It turned out that Fred explained to my mother's relatives that she prefered money as a birthday gift and collected the gift money from everyone. The cash he returned as his debt in the envelope was not his. Everyone else thought he was presenting the joint gift, except for my mother, who was made to believe that he was repaying his debt.
After that my mother stopped bugging her uncle Fred. It became clear she couldn't match his superb skills in escaping his debts.
Suppose you are a woman living in the US and you would like to be a mathematician and work in academia. Suppose also that you would like to have children and spend some time with them. Let us say that you want two or three children and you would like to be with them at home for at least their first two or three years. That is, in total you need to devote 5 or 6 years to this endeavor. When would be a good time for you to have children? American women mathematicians are commonly advised to postpone having children until tenure.
Let us look at the situation more closely. Is it a good idea to have children before you earn your PhD? There are many non-mathematical reasons not to have children too early:
There are also mathematical reasons not to have children too early. My former adviser Israel Gelfand liked to tell everyone that mathematicians generate all their best ideas before the age of 23. His views may be extreme. After all, we know of mathematicians who made great discoveries later in life, but it could be that they did this using their mathematical wisdom rather than the processing power of their brains. It may well be beneficial to start your first research early in life. I am not sure about math creativity, but I swear that it is much more difficult to learn new things as I age.
In addition, you might need to relocate frequently to maintain your math career and it is more difficult to do that with children. It's hard on the children too. Besides, having children early means that while working on your tenure, you will be distracted by your kids and their problems, leaving you less time for your research.
You might think that the closer you get to your PhD, the more the situation improves. In reality, there is a very important reason not to have children while you are in grad school. When you start working on your first topic, it is very important not to be interrupted. If you take a big break someone might finish what you started. When you come back, your topic might be resolved and you would have to start all over again.
The situation after graduate school is even worse. When you apply for jobs, employers are likely to count how many papers you have published per year after your PhD. So you need that number to be high. You can't afford to dilute your paper count per year by a several-year break. Besides, if you have an interruption in your research it might be considered as a weakness and you might lose in comparison with other applicants. Let us break down the time between PhD and tenure into three periods: postdoc, visiting positions, and tenure track. For each period there are extra reasons not to have kids:
For all of these reasons, advice to wait until tenure makes sense. There is one big problem with it though: you usually get tenure in your late thirties. It might be too late for children. You might not want to risk that.
You can always compromise by having one child instead of three. Or you can suppress your desire to spend a lot of time with your children by having hired help, which means that you will miss a good deal of your child's development, and your child will miss a lot of your love. You can compromise your academic goals by taking a more stable, but less research-oriented, technical job in industry. Or you might get lucky and marry a househusband.
In short, a math career is very kids-unfriendly — there is no right time. If you're a woman mathematician who wants to spend time with your kids, prepare for pain and disappointment.
But here is an unconventional idea you might consider.
After you finish working on your PhD, postpone your actual defense by 5 years, and have your kids in between. This way all your PhD results will be published and no one can interfere with them. At the same time, the clock that counts your publications per year after your PhD will start 5 years later.
My idea is not a good solution — you will still have many problems — but it might be better than waiting 'till tenure. I do wish there were a better way.
Here is a logic puzzle for kids:
— John has more than a thousand books, said Pete.
— No, he has less than one thousand books, said Ann.
— Surely, he has at least one book, said Mary.
If only one statement is true, are you sure you know how many books John has?
Here is a math problem from the 1977 USSR Math Olympiad:
Let A be a 2n-digit number. We call this number special if it is a square and a concatenation of two n-digits squares. Also, the first n-digit square can't start with zero; the second n-digit square can start with zero, but can't be equal to zero.
Obviously, these questions are divided into two groups: show the existence and estimate the bound. Furthermore, this problem can be naturally divided into two other groups. Do you see them? The puzzle about special numbers makes a special day today — you get a four-in-one puzzle.
David Bernstein gave me this puzzle. He says that the puzzle was given at a Moscow math Olympiad a long time ago. At that time there were no computer science olympiads yet. I do not know why this puzzle feels to me like computer science. Maybe because the trivial solution is of order N, the easy solution is of order square root of N and the requested solution is of order logarithm of N:
Can you cut a square into N convex pieces minimizing the number of possible intersections of any straight line with your pieces?
It is easy to maximize the number of intersections. If you cut your square with N-1 parallel cuts into N equal thin rectangles, then there exists a line with N intersections.
It is easy to cut a square to guarantee no more than 2√N intersections. Can you cut your square so that any line makes no more than 2log2N intersections?
I am interested in a career in mathematics. How hard is it to be a woman mathematician?
Let us look at some numbers from the American Mathematical Society Survey Reports for the year 2005:
You can't just say that women do not like math — 40% of those choosing math as a major is quite a large number, after all.
On the other hand, the downward trend of these percentages is striking. If women's opportunities and abilities are the same as men's, these percentages should grow with every age step, since, as we know, the percentage of women in the population increases with age due to men dying earlier.
But the numbers go down and very fast. There are many potential explanations for this, but today we're going to look at one of them:
Women have less ability for high-level mathematics.
Was Larry Summers right when in his speech that cost him his Harvard presidency he compared math ability to height and to the propensity for criminality, and suggested that the distribution, especially standard deviation, of math ability differs for men and women?
To answer this question, I wanted to find some other data that correlates gender with math abilities. I took the results of the American Mathematical Competitions (AMC 12) for the year 2008. Among 120,000 students who participated, 43% were females. Here are some results:
This picture is similar to that of the academic career: the closer you climb to the top, the smaller percentage of girls you see there. Of course, winning a competition is very different from getting tenure. People who win competitions are smart and competitive — smart and competitive enough to go for money, rather than academia. On the other hand, people who are interested in mathematics often are not interested in anything else. Why would they waste their time in competitions when the Riemann Hypothesis is still waiting to be solved?
But still, both achieving tenure and winning math competitions represent mathematical ability in some sense. If Larry Summers was right and the distribution of math ability is different among males and females, then by looking around you at the percentage of females at your level, you should be able to assess how close you are to the top of the math field.
I propose the following math career predictor: Take your results in AMC 12. If among kids who did better than you, the percentage of girls is more than 11%, you do not have a chance at tenure. If the percentage of girls is more than 30%, do not waste your time working on a math PhD. If the percentage of girls is more than 40% maybe math majoring is not for you.
I hate my math career predictor. I hate it not only because it has so many flaws that it might just deserve the Ig Nobel Prize, but because it doesn't take people's effort into account. You really have to work very hard to be a math professor, whether you were a winner or a loser in math competitions.
You might ask why I created a math career predictor that is so flawed. My mathematician friends, those who are more honest than polite, tell me that I have no chance at getting back to academia. On the other hand, I had the second best result at the 1976 IMO, which means I have the ability. My predictor may be my only hope.
A puzzle from the 1977 USSR math Olympiad can be solved naturally with linear algebra:
Seven dwarfs are sitting at a round table. Each dwarf has a cup partially filled with milk. Each dwarf in turn divides all his milk evenly between the six other cups. After the seventh dwarf has done this, every cup happens to contain the initial amount of milk. What was the initial distribution of milk?
Can you use linear algebra to intelligently solve this puzzle?
One of the questions from the Microsoft employment interviews for creative thinkers is: "How would you design Bill Gates' bathroom?" I gave this question to my students at the Advanced Math and Science Academy Charter School. Most of them started by suggesting it be big and gold, but they also suggested more interesting ideas:
Tell me your own ideas.
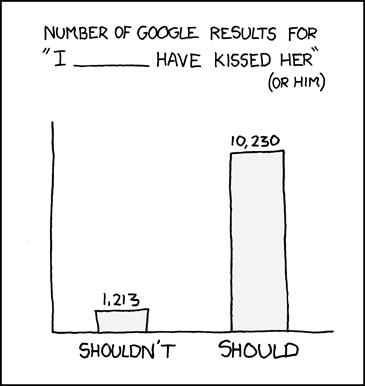
I recently updated my collection of my favorite xkcd webcomics.
Today I would like to discuss the comic entitled "Regrets". When I saw this comic, the first thing I did was go to Google to check the numbers. All my numbers were taken on September 9, 2008 at around 3:00 p.m.
Here are the Google hit counts:
The numbers are slightly different than those in the cartoon, but the idea is the same; we regret we didn't kiss. Does it mean that if you want to kiss someone you should go ahead, or otherwise you would contribute to this pile of regrets? The answer is coming later, but first, let's see what happens if we change gender:
The same story overall, but for some reason, there are fewer reports by people who either tried or didn't try to kiss HIM. Is kissing him less interesting or important? Most probably we still expect men to take the initiative in kissing her.
Then I checked the genderless case:
Wow. Looks like we really should start kissing each other. Right? But wait. Let's check the point of view of a kissee, rather than a kisser:
We see a completely different picture. It is easy to explain why the numbers are smaller: passive people would be less likely to discuss their feelings. But, even so, they claim that they preferred not to be kissed. Maybe it is OK that people mostly regret that they didn't kiss. After all, if they had tried to kiss, they might not have been greeted with enthusiasm. This leaves you with a choice between your own regrets that you should have kissed and his/her regrets after you did.
I did regret that I hadn't kissed you, but I so much prefer that I regret not kissing you than you regret being kissed by me. This small research made me feel better. I will not continue regretting any more.
Ken Fan is running a math club for girls in Cambridge, MA, called "Girls' Angle". When I heard about it, my first reaction was surprise. When I was a girl, I would never have been interested in a girls-only math club.
Am I prejudiced? When I was growing up in Russia, there were not very many girls who were really good at mathematics. I would have expected that a girls' math club would be less challenging than just a math club.
What if someone organized a boys-only math club? I would have been furious. I would have felt it was discriminatory. Should I then feel an equivalent fury about the girls' club? But I do not feel furious, and I wonder why. Is it because deep down I think no boy would bother being interested in joining a girls' math club? Is it because I still think a girls' club would be weaker than a general club? I do not know.
At the same time I agree with Ken, for there are a variety of reasons why girls might prefer a girls-only club. For example, shy girls might feel more comfortable with girls or some girls might feel better able to concentrate without the distractions of boys. In some cases, the parents might have made the decision.
Obviously, since the club has students, there is a demand for it. If there is a demand, there should be a supply. I will support anything that works and helps improve American math education. I even volunteered to give a guest lecture at Girls' Angle.
Was my lecture at the girls' club different from my other lectures? Yes, in a way. I asked the girls to help me to finish a sequence. I started writing 1, 1, 2, 3, 5, 8, on the board and no one was shouting the next number. In great surprise I turned back to face the class and saw a forest of raised hands. They patiently waited for my permission to speak. Yes, it felt different.
I decided to check the pricing. It appears that the girls club is twice as cheap as other math clubs, like The Math Circle or S.M.Art School. I can't help but wonder if the girls are signing up at the Girls' Angle not because they want to study in the girls-only group, but because it is cheaper.
I am glad that Ken Fan is good at finding sponsors and that there are so many people sympathizing with his cause. However, this situation does seem unfair to boys. Should I be furious that boys are not allowed in this very affordable math club? I do not feel furious, but I decided not to give any more lectures at Girls' Angle for free. At least not until I give a free lecture to a mixed-gender math club. I want to be fair.
This puzzle is a generalization of a problem from the 1977 USSR math Olympiad:
At the beginning of the game you are given a polynomial, which has 1 as its leading coefficient and 1 as its constant term. Two people play. On your turn you assign a real value to one of the unknown coefficients. The person that goes last wins if the polynomial has no real roots at the end. Who wins?
It is clear that if the last person's goal is for the polynomial to have a root, then the game is trivial: in this case, he can always make 1 a root with the last move. Also, an odd degree polynomial always has a real root. Therefore, to make the game interesting we should assume that the degree of the polynomial is even.
Though I can't imaging myself ever being interested in playing this game, figuring out the strategy is a lot of fun.
Here is a math puzzle for kids from a nice collection of ThinkFun Visual Brainstorms:
Wendy has cats. All but two of them are Siamese, all but two of them are Persian, and all but two of them are Maine Coon. How many cats does Wendy have altogether?
This puzzle has two answers: the expected answer and an unexpected answer. Can you find both?

Chris Burke gave me his permission to add his webcomics to my collection of Funny Math Pictures.
This comic doesn't qualify as a math picture, but it is geeky enough for me to like it.
Here is an arithmetic problem for you:
You have $700 dollars in your checking account. You are sloppy and forget how much you have. You write three checks for $600, $200 and $200. For every bounced check you are fined $25 by your bank. How much in fines will you have to pay for your sloppiness?
Solution: the fine depends on the transaction order. If they process your $600 check first, you will have two bounced checks. If they process a $200 check first, then only your $600 check will bounce.
The question is, what will your bank do if all three checks need to be processed at the same time? There are three options:
Assuming the worst — your bank is evil — what is the answer to the problem? Do you think you will be fined $50? If so, you are wrong. The company to whom you wrote the check will fine you too. Supposing that the company has the same $25 fine as the bank, can we say that you will be fined $100? Nope, this is not correct either. You are forgetting that companies will reprocess your bounced checks two days later and the checks will bounce again. You will be fined twice for each check by two different entities. Thus, you can face $200 in fines.
My next question is: what do you think is a fair fine in my arithmetic problem above?
Banks and companies have never heard of double jeopardy and do not think that it is unconstitutional to fine you twice for the same mistake. No doubt, the second reprocessing of your checks is done "for your convenience". "For your convenience" they assume that the bouncing was due to a computer glitch, so they should reprocess your check immediately after it has bounced. "For your convenience" no-one will disturb you to notify you that your checks are bouncing. I also believe that if your fine depends on the random order of processing of checks, the banks should be graceful and shouldn't pick the more profitable order for themselves. I do think that charging you more than $50 in my example is against the law and is not fair.
The law should protect us against entities that rob us "for our convenience."
I added some new jokes to my collection of math, computer and geek humor:
* * *
— What do you do to protect yourselves from viruses?
— We use disposable computers …
* * *
Microsoft offers a new service. They sell ad spots in their error messages.
* * *
Sysadmin:
— I do not care if everyone insists that using the name of my own cat as a password is a bad idea! RrgTt_fx32!b, kitty-kitty-kitty …
* * *
Due to technical difficulties the release of Windows 2000 is delayed until February 1901.
* * *
A doctor looking at patient's X-rays:
— Hmm, multiple hip fractures, tibia and fibula fractures. Oh well, Photoshop can fix all that.
* * *
After learning how much money Bill Gates has, Satan offered him his own soul.
* * *
Question: What did one math book say to the other?
Answer: Don't bother me. I have my own problems.
* * *
Student: Teacher, would you punish me for something I didn't do?
Teacher: No, why?
Student: I didn't do my homework.
* * *
— My teacher said we would have a test today, rain or shine.
— Then why are you so happy?
— Because it's snowing.
* * *
Question: How many sides does a box have?
Answer: Two — the inside and the outside.
* * *
Question: What did the calculator say to everyone?
Answer: You can count on me.

Just updated my collection of Funny Math Pictures.
Here is a puzzle that my ex-brother-in-law, Dodik, gave to me today:
Prove that every group with more than two elements has a non-trivial automorphism.
I usually love puzzles that are solved with a counter-intuitive brilliant idea. This puzzle is different — I didn't solve it in one elegant swoop. But I still love the puzzle: it feels so natural, and it's solution feels so natural, that I even decided to call this puzzle "organic." Or, maybe, I am just in an organic mood today waiting for my organic bananas to be delivered from Boston Organics.

Here is a funny puzzle from Kvant (1996, vol 4), the best Russian journal of recreational math.
When Alice goes through the looking-glass, she might meet many multi-headed, multi-armed, multi-legged beings. A being with H heads, A arms and L legs is considered:
Can there exist a well-rounded personality behind the looking-glass: someone who is smart, strong and fast at the same time?
Once I witnessed John H. Conway factoring large numbers in his head. Impressed, I stared at him. Encouraged by my interest, he told me that if I ever want to be able to factor large numbers, I should know all the primes below one thousand.
The secret to knowing all such primes is to remember the composites, he continued. Obviously, we don't need to remember trivial composites — the ones divisible by 2, 3, 5, or 11. Also, everyone knows all the squares below one thousand, so we can count squares as trivial composites. We only need to remember the non-trivial composites. There are not that many of them below one thousand — only 70. I mean, 70 is nothing compared to the number of primes: 168.
So, I need to remember the following seventy numbers:
91, 119, 133, 161, 203, 217, 221, 247, 259, 287, 299, 301, 323, 329, 343, 371, 377, 391, 403, 413, 427, 437, 469, 481, 493, 497, 511, 527, 533, 551, 553, 559, 581, 589, 611, 623, 629, 637, 667, 679, 689, 697, 703, 707, 713, 721, 731, 749, 763, 767, 779, 791, 793, 799, 817, 833, 851, 871, 889, 893, 899, 901, 917, 923, 931, 943, 949, 959, 973, 989.
If you are very ambitious and plan to learn the primes up to 50,000, then the trick of learning non-trivial composites instead of primes is of no use to you. Indeed, for larger numbers the density of primes goes down, while the density of non-trivial composites stays about the same or increases very slightly due to a smaller number of squares.
The turning point is around 11,625: the number of primes below 11,625 equals the number of non-trivial composites below it. So, compare your ambition to 11,625 and tailor your path of learning accordingly.
If you are lazy, you can learn primes only up to 100. In this case your path is clear; you should stick with remembering non-trivial composites, for you need to remember only one number: 91.

One of Microsoft's biggest contributions to humanity is the popularization of manhole covers. The most famous question that Microsoft asks during job interviews of geeks is probably, "Why are manhole covers round?" Supposedly the right answer is that if a manhole cover is round it can't be dropped into the hole. See, for example, How Would You Move Mount Fuji? Microsoft's Cult of the Puzzle - How the World's Smartest Company Selects the Most Creative Thinkers. This book by William Poundstone is dedicated exclusively to Microsoft's interview puzzles.
All we need, actually, is for the cover not to fit into the hole. For example, if the hole is small, the cover could be almost any shape, as long as the diameter of the cover is bigger than any straight segment that fits into the hole.

Microsoft makes an implicit assumption that the cover is about the same shape and size as the hole; otherwise we would waste a lot of extra cover material.
Even with this assumption, there is a good deal of flexibility in possible shapes if our only concern is that the cover shouldn't fit into the hole. It is sufficient for the cover to be any shape with a constant width.
Here are some additional answers to why the cover should be round. Microsoft accepts the answer that a round cover is easier to roll. I'm not sure why a cover would ever have to be moved away from its hole. But I agree that if kids try to steal a cover, it would be much easier to escape with a round one.

Another answer that Microsoft supposedly accepts is that you do not need to rotate a round cover to align it with the opening when you are putting it back. This way if there is a lane divider painted on the cover it will point in a new random direction.
You can find many other explanations at the wiki article devoted to this subject. The most reasonable is that manhole covers are round because manholes are round. Duh!
Thanks to Microsoft there are now many websites with pictures of and discussions on the shape of manhole covers. For example, Manhole Covers Etc. or Manhole.ca or Manhole Covers of the World. As you can see many manhole covers are square or rectangular. They say that New Hampshire had triangular covers at some point.
But my favorite answer to this interview question was sent to me by Jorge Tierno:
Since manhole covers are not necessarily round, but you are asking why they are round, you are probably asking why round manhole covers are round. Round manhole covers are round by definition.
Now I have my own favorite question to ask you during a job interview: "Why are some manhole covers square?"
For his Master's thesis, my son Alexey Radul wrote the Symmetriad — a computer program to compute and display highly symmetric objects.
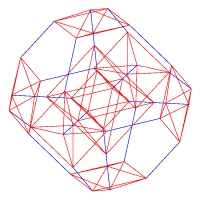
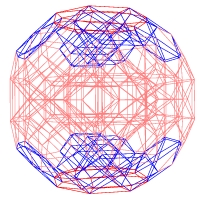
The objects the Symmetriad is after are the 4D generalizations of Platonic and Archimedean solids. His thesis contains a picture gallery made with the Symmetriad, and these are my three favorite pictures.
The pictures have cute titles. The problem is that I still haven't installed the Wordpress plugin that allows me to put captions under the pictures. That is why you have to guess which title matches which picture. The titles are: "The Planets are Aligned," "Great Jaws," and "Diamonds are Forever."
If you are wondering why one of the pictures shows a non-connected object, in fact the object is connected, but some of the edges are white, so that you can better see 3D cells of the object.
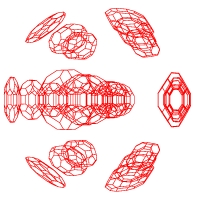
Subsequent to the publication of this thesis, Alexey enhanced his software to make even more dramatic pictures. The following pictures have no titles, so feel free to suggest some:



I think it would be nice to publish a book with all these pictures. As a book on symmetries should be published on a symmetric date, the next opportunity would be 01.02.2010.
I resigned from my job half a year ago. If you remember I was planning to rebuild my career in academia and to find myself along the way.
The problem with re-entering academia is that to find a job starting September 2008, I would have had to apply in December 2007. I really didn't want to apply before finding my new direction in mathematics and publishing some papers to rebuild my name. So I decided to apply for academic jobs in December 2008, while using the intervening year for research and to try to publish.
The problem with delaying the start of my new academic job until September 2009, is that I didn't save enough money to cover such a long period of time. Even though I cut down my expenses significantly, I still need some additional income in the meantime. However, temporary jobs consume the time I need for research in order to go back to academia. To resolve this Catch-22 situation, I decided to choose jobs of only two kinds: first, either they pay a lot, so for a limited time of work I can buy a lot of extra time for my research; or second, they're aligned with my goals. I wasn't yet looking very hard for work, but nonetheless several jobs came my way.
One of the jobs I accepted was a temporary job as a math competition coach at Advanced Math and Science Academy (AMSA) Charter School. This gave me a chance to check once again how I feel about teaching. I love entertaining people with mathematics. I showed magic tricks to my students, played games with them and so on. I enjoyed myself; my students liked me. But I do not know enough tricks or games to teach 24 hours a week as a regular school teacher. I decided that I really do not want to be a school math teacher. But I love being a coach, because it takes less time and I get the best kids.
I also worked on the Organizing Committee for the Women and Mathematics Program in Princeton in May 2008. The irony is that I lived in Princeton for seven years and ignored this program for most of them. Initially I was prejudiced against such a program. I felt that I should go to lectures only for their mathematical value. The gender of the lecturer doesn't matter.
I think I was missing the whole point of the program. I should write about this program more.
The surprising result of the last half year is that I am having a blast blogging. Wouldn't it be fabulous to find a job in mathematical journalism, if such a profession exists.

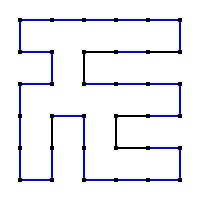
I love Grand Tour puzzles more than I love Sudoku. You are given a graph, for example, a square grid like the one on the left. Some edges are highlighted. You need to find a closed path that visits each vertex exactly once and includes the highlighted edges as part of the path. Mathematically speaking you need to reconstruct a Hamiltonian circuit on a graph, once you are given a part of it. The highlighted edges are chosen to guarantee a unique solution to the puzzle.
On the left you can see a sample grand tour problem with its solution. This puzzle was designed by Glenn Iba. On Glenn's Grand Tour Puzzle Page you can find many grand tour puzzles of varying levels of difficulty. The puzzles are playable. That is, you can click or unclick an edge. You can also branch out in a different color, which is especially useful for difficult puzzles when you want to test a hypothesis. I just want to warn you: these puzzles are addictive — I couldn't stop playing until I solved all of them.
Below there is a simple grand tour puzzle from Glenn's collection, but this time on a triangular grid:
You do not need a grid to construct a puzzle. But these puzzles look very natural on grids. I tried to analyze square grid puzzles a little bit. The first important point is that for square grids with odd number of vertices on each side of the square, Hamiltonian cycles do not exist. This point is easier to prove for directed Hamiltonian cycles. You can make a directed cycle from an undirected one by choosing a direction. If you have a directed cycle on a square grid, then the number of edges pointing up should be the same as the number of edges pointing down. We can say the same thing about edges on the cycle pointing left or right. Hence, the number of edges of a Hamiltonian cycle on a square grid should be even. At the same time, the number of edges of any Hamiltonian cycle equals the number of vertices.
I just proved that you need only consider square grids with an even number of vertices on each side. For square grids with two vertices on each side, there is only one Hamiltonian cycle, namely the border of the square. The only grand tour puzzle for this grid won't have highlighted edges at all. For a square grid with four vertices on each side there are only two different Hamiltonian cycles up to isomorpshisms:
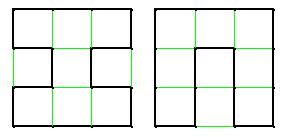
If we count all the reflections and rotations, we will get six Hamiltonian cycles. The next picture shows all 11 grand tour puzzles on this grid. If we count rotations and reflections, we will get 66 different grand tour puzzles.
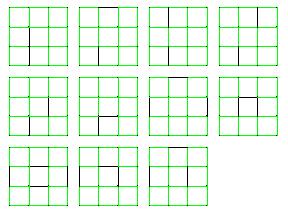
Below are the sequences associated with this puzzle. Except for one case, I do not know if these sequences are in the Online Encyclopedia for Integer Sequences. I don't know because I only counted two terms of each sequence and this information is not sufficient to identify the sequence.
If you look at Glenn Iba's 6 by 6 square grid puzzles you can see that the smallest number of edges is not more than 6. And the largest number of edges is no less than 12.
You can also make similar sequences for a triangular grid.
I invite you to calculate these sequences and submit them to the OEIS, if they are not already there.
Start is the STate of the ART question-answering system. You can ask Start any question in plain English — for example, "What is the population of Moscow?" — and instead of producing millions of pages like Google, it provides one exact answer: "The population of Moscow, Russia, is 8,746,700." I am not sure where this number comes from, as Russian sites suggest that the population of Moscow is more than 10 million people. But anyway, back to my challenge.
I have my email address in plain sight on my webpage. As a result, I get a lot of spam. So, I am thinking about a way to present my address so that humans can easily deduce it, but computers can't. Here it is: my email server is Yahoo and my user name consists of 7 lower case letters. Each letter answers one of the questions below, in the right order. As of today, Start can't answer any of these questions.
The advantage of presenting my user name in this manner is that I will restrict my new correspondence to people who are sufficiently eager to write to me that they can spare ten seconds figuring out my email address. The main advantage is that Start can't answer these questions, giving me hope that spamming software can't do it either.
I do think that the state of the art question-answering system should know the first letter of the alphabet. Start: these questions are a challenge for you. How much time will it take you to do it?
Watch out. Maybe Google can do it faster.
I'm not kidding; there is such a paper. It is titled, "A Headache-causing Problem" and its authors are Conway (J.H.), Paterson (M.S.), and Moscow (U.S.S.R.). The acknowledgements in the paper shed some light on how Moscow became a mathematician:
The work described here was carried out when the first and second named authors enjoyed the hospitality of the third. The second and third authors are indebted to the first for expository details. The first and third authors gratefully remark that without the constant stimulation and witty encouragement of the second author this paper
[The next part was meant to be on the following page, Conway told me, but the editor missed the humor and just continued the sentence…]
was completed.
As a consequence of this joke, Moscow is envied by many mathematicians as it has an Erdős number of 2. Now wait for a couple of hundred years, and Moscow will be the only living mathematician with an Erdős number of 2. I can just imagine future mathematicians trying to persuade Moscow to coauthor papers with them, because this will be the only way for them to score an Erdős number of 3.
Even though I lived there for 30 years, I had no idea that Moscow had a talent for math. Of course, this talent only emerged when Moscow was more than 800 years old.

This wonderful paper by Moscow was very difficult to find. It was presented to Hendrik W. Lenstra on the occasion of his doctoral examination. It was published in 1977 in a book titled "Een pak met een korte broek," which in Dutch means, "A Book in Short Trousers."
I tried to find it on the Internet — it wasn't there. I asked John Conway — it took him quite some time to find it. Here is the picture of John Conway searching for a headache-causing problem. Luckily for you and me, he found it. To save you from another headache, I am uploading the scan of it in pdf format here: A Headache-causing Problem by J.H. Conway, M.S. Paterson, and U.S.S.R. Moscow.
I hope that Moscow will not start complaining that I never asked its permission to post the paper. Some might argue that Moscow, U.S.S.R., doesn't exist anymore, but I would counter that it exists, but with a changed name. If Moscow tries to sue me, I hope it's not because it is still bitter that I left it behind in 1990.
Hey Moscow, it's time we were friends again. Would you like to co-author a paper with me?
I resigned from BAE Systems on January 3, 2008. At the beginning of a year, it often takes time for people to adjust to writing the new number. Probably out of habit, someone somewhere wrote that I resigned in January, 2007. The computer at my medical insurance company Cigna got overexcited. It noticed that Cigna paid all my medical bills for 2007, a period for which, according to that creative but premature resignation date, I was ineligible. In its zeal Cigna retracted the money that they had already paid to my doctors for all of my 2007 visits.
In an instant, I became a delinquent; my doctor bills were suddenly more than a year overdue and my credit score probably plummeted. My taxes became suspect, too. I had claimed that I had medical insurance on my Massachusetts taxes, which now Cigna wouldn't confirm.
While Cigna was racing to get their money back from my doctors, they conveniently forgot that I and BAE Systems paid a lot of money for their insurance. They didn't hurry to return this money. At one point I was thinking I would be richer if I got back the money paid to Cigna for my insurance and paid the doctors myself.
I had a conference call among Cigna, my former employer and myself. My employer confirmed that I had Cigna coverage until January, 2008, but this was not enough. Cigna insisted that it needed "computer confirmation," even though it was their shoddy computer work that caused all this trouble.
After many phone calls and conference calls, finally Cigna admitted that I am right and reinstated my medical insurance coverage for the year 2007.
Can you guess what happened next? I received a new bill from my doctor. Cigna reinstated me, but didn't pay the money back to my doctors. Now there was another round of phone calls and conference calls.
As of today, the time and nerves I spent to resolve this issue exceeded the money Cigna owes to my doctors and I am still waiting for the money to be transferred.
If they are fighting so hard not to pay their debt of $1,000, I wonder about the financial situation of this company. I would definitely consider it very risky to buy Cigna stocks.
Recently I published my ideas for a Flexible Zipcar Algorithm that allows customers to rent Zipcars one-way. I had a dream the night after I published it: the Zipcar research lab invited me to give a presentation about my algorithm and they asked me a lot of questions. I would like to answer these questions now, but first let me give you a short description of the algorithm:
Some locations are flexible. The number of cars assigned at a flexible location is not fixed, but rather a range between the minimum and the maximum. A Zipster would be allowed to use a car one-way from one flexible location to another, as long the number of assigned cars doesn't move outside the range.
Question. Zipsters expect to pick up the exact vehicle they reserved. With vehicles changing locations you will break this system. I am operating on the assumption that Zipsters will continue to pick up the exact vehicle they reserved.
Question. What about people who get attached to the cars at their location? You can divide your pool of cars at a flexible location into two groups: fixed Zipcars and floating Zipcars. Only floating cars will be allowed to move. You should advise Zipsters who get attached to their cars to choose fixed cars as the object of their affection. This solution is less flexible, but it resolves your problem.
Question. You designed your algorithm using the min and max number of cars at a flexible location. Where is the desirable number of cars coming from? We need the desirable number of cars to calculate the financial incentives. For example, you can take the absolute value of the difference between the current number of cars at a flexible location and the desirable number of cars. Then sum it up over all locations. We can call this total the distance between the current state and the optimal state. If a one-way trip increases this distance, that Zipster pays extra and vice versa. You can also add a surcharge for all one-way trips to cover the extra expense for parking spaces.
Question. What if cars get stuck? For example, what if we always have the maximum number of cars at Harvard Square and the minimum number of cars at Coolidge Corner? You can always offer free rides from Harvard Square to Coolidge Corner. If every Zipster knows that you have a discount program which is easy to find, your cars will be in the right place in no time. For example, you can color code overstaffed and understaffed locations on your map; or you can add RSS feeds for people who are interested when cheap rides from Harvard Square to Coolidge Corner are available.
Question. Are you saying that instead of hiring drivers to move our cars around we find a much cheaper Zipster who needs to go in the same direction? Yes. If you go even further and offer a token payment or some Zipcar credits, you can have Zipsters driving your cars to oil changes and car washes for you.
Question. Why do you always talk about a small number of flexible locations? I would limit the number of flexible locations for your initial stage, so that for a small investment you get something new, you can experiment, you can observe and study trends in how cars are migrating, you can tune your financial incentives system and you can design and test your web support for this algorithm.
Question. What if someone reserves a car for a one-way trip one month in advance? What happens with the car during this month? If your car – let's name it "Comfy" — is reserved from the Harvard Square location for a month from now, you need to lock this car into the Harvard Square location for a month. That means, no one can take Comfy for a one-way trip during this month. This looks like a bad case of inflexibility. To resolve it you can have a time-limit for one-way reservations. For example, you might limit one-way reservations to not more than three days in advance.
Question. Suppose we have four cars at the Harvard Square location and the desirable number is three. Then four people reserve four different cars at this location for round-trips on Labor Day. Are these four cars stuck at Harvard Square for a month until Labor Day? I can offer one solution using the earlier idea of fixed and floating cars. You can allow very advanced reservations for fixed cars, but floating cars can only be reserved three days in advance. Another possible solution is that you do the same without dividing your cars into fixed and floating. For example, you allow people to have very advanced reservations for any car which is currently assigned to the Harvard Square location. As soon as three cars are reserved for more than three days in advance, the fourth car is no longer available for very advanced reservations. The fourth car temporarily starts behaving like a floating car, without that being its permanent designation.
Question. Suppose today is Monday and Jack reserves Comfy one-way from Harvard Square to Coolidge Corner for Thursday. To which location is Comfy assigned for three days between Monday and Thursday? On one hand it should be assigned to Harvard Square as it takes a parking space there and we can't allow another car to take up that space. Also, Comfy is available for reservations before Thursday at Harvard Square. At the same time, Comfy can't be counted as an extra car anymore as we know that it is guaranteed to be moved. That means that even though Harvard Square actually houses an extra car for these three days, it shouldn't be flagged as a location with extra cars that need to be reassigned. On the other hand, Comfy will take a spot at Coolidge Corner soon, so we can't allow other cars to move into that spot. Even though Coolidge Corner doesn't yet have the complete set of cars, we can't allow other cars to take up Comfy's future spot.
Question. It sounds complicated. Can we make it simpler? You can simplify this design for the first implementation. For example, you can only allow immediate one-way reservations. That eliminates any problem with conflicting reservations or an extra car holding up a space for three days. Also, keep in mind that the user doesn't need to see all this complicated stuff. They are only interested in knowing whether or not they can reserve a car.
Question. What if someone reserves the car one-way then cancels the reservation? This only becomes a problem if someone else reserves the same car for a later time at the destination. In this case, you might institute a very big fee for cancellations of one-way reservations, so that you can either hire a driver or offer a super deal to other Zipsters. Of course, if you allow only immediate reservations for one-way cars this problem will be minimized.
Question. Suppose Jack reserves Comfy for two hours; his starting point is Harvard Square and his end point is Coolidge Corner. Where is Comfy assigned during these two hours? This is a great question. For round-trip Zipcars, you do not care if a person starts a half-hour late or returns the car one hour early. With a one-way car, you need to know when Comfy's parking space will be available to other cars. To allow Jack to pick up his car as late as he wants or return it as early as he wants, the simplest solution is to assign Comfy for two hours to both locations. That is, no other car is allowed to move into Comfy's parking spot at Harvard Square until the end of Jack's rental period and the spot for Comfy should be ready at Coolidge Corner from the start of Jack's rental period.
Question. You were talking about the simplest solution. Do you mean you have other solutions? I have many ideas, but I prefer to get some feedback from the car-sharing research community before continuing.
Hey, Zipcar! Let's do it!
Suppose N mothers live in a city. Half of them have one child and half of them have two children. That means that an average mother has 1.5 children.
Suppose we pick the sexual orientation of every child by rolling dice. Let's assume that a child has a 10% probability of being homosexual.
The number of mothers with one child who is homosexual is 0.05N. The number of mothers with two children both of them homosexual is 0.005N. The number of mothers with two children with only the first child homosexual is 0.045N, which is the same as the number of mothers of two children with only the second child homosexual. The total number of mothers who have two children with at least one of them homosexual is 0.095N.
Let's calculate the average fertility of a mother with at least one homosexual child. It is (1*0.05N + 2*0.095N)/(0.05N + 0.095N) = 0.24/0.145 = 1.66. The resulting number — 1.66 — is much bigger than 1.5, the average number of children for a mother.
This means there is a correlation between homosexuality and the fertility of mothers. This suggests that there is a gay gene which at the same time is responsible for female fertility.
But the model is completely random — there can't be any correlation.
Where is the mistake?
Obviously, you can substitute homosexuality with having blue eyes or math ability or whatever, but I invented this paradox while I was working on my "Fraternal Birth Order Threatens Research into the Genetics of Homosexuality" post. Besides, there is some research on correlation between homosexuality and fertility.
I look forward to your solution to this puzzle.
Three years after I moved to the U.S. and had my second child here, I got an NSF postdoc position at MIT. I had had a long break from my previous research in integrable systems, so I decided to start something new for me — quantum groups. Soon afterwards I invented tetramodules and published a paper about them.
Some time later a friend of mine showed me some papers where my tetromodules had been described long before me. I felt such pain, that I couldn't work.
I was ashamed that the quality of my paper was compromised. I was very scared that someone might think that it wasn't original work. I felt worthless for having wasted so much energy on something that was already known.
Afterwards, I discovered that tetramodules appeared in the literature under many other names: bidimodules, Hopf bimodules, two-sided two-cosided Hopf modules, 4-modules, bicovariant bimodules. That meant that many people were reinventing them at the same time. I felt slightly better knowing that I wasn't alone, but was in fact part of a crowd. Still, my pain impeded my ability to work and do research.
I have just read an article in the New Yorker entitled "In the Air" about some famous discoveries made simultaneously by several people. It made me realize that I am still not over that tetramodules story from 15 years ago.
Being a mathematician requires one to be emotionally strong. You need high self-esteem. Do I need to overcome my emotions or is there a niche for very emotional mathematicians? Perhaps blogging about math is such a niche.
According to a famous study: " [E]ach older brother increases a man's odds of developing a homosexual sexual orientation by 28%-48%."
This means that sexual orientation is not uniquely defined by genes in the way that our blood type is defined. Indeed, if homosexuality was similar to blood type, the probability of giving birth to a homosexual would be the same for the same parents, independently of birth order. Furthermore, the fact that identical twin brothers quite often have different sexual orientation also supports my claim that it isn't like blood type. On the other hand, there is some research that shows that there is a genetic component to sexual orientation. This might mean that there are genes that increase a predisposition in a man to become gay or it could be that there is a gay gene which determines their homosexuality for some part of the gay population — or both.
The research into a genetic component of gayness shows that there might be some genes in the X chromosome that influence male homosexuality. It also shows that the same genes might be responsible for increased fertility in females.
By the way, this fascinating research provides an explanation of why "gay genes" — if they exist — do not die out, as evolutionary laws might lead us to expect.
The theory that the probability that someone will be gay is dependent on the fraternal birth order impacts in several interesting ways on the whole field of research into the genetics of homosexuality.
Let us create a theoretical model where homosexuals would be born randomly with a fixed probability if they are the first sons of a woman, and increasing probability for subsequent sons. In this model there would be two interesting consequences:
My point is that all genetics research on homosexuality should take into account these two consequences and adjust for them. That means that it is not enough to show that brothers are more likely to be homosexual in order to prove that there is a genetic component. It needs to show that the correlation between relatives is much stronger than the correlation resulting from the birth order.
For people who are not mathematicians, I will build simple models that illustrate my points. Let us consider some extreme theoretical examples first.
First model. Suppose mothers only give birth to sons and only to one or two sons. Suppose the first son has a zero probability of being gay (which means that first sons are never gay) and the second son has a probability of one of being gay (which means that second sons are always gay). Then all mothers of gay men will have two sons, while mothers of random boys will have somewhere between one and two sons. Another result will be that all gay boys in this model will never have a gay brother.
Second model. Suppose mothers only give birth to one or three sons. Suppose the first son has a zero probability of being gay and the second and the third sons have a probability of one of being gay. Then all mothers of gay men will have three sons, while mothers of random boys will have somewhere between one and three sons. Another result will be that all gay boys in this model will always have a gay brother.
Third model. Let us take some more realistic numbers. Let us consider only the case of women who have one or two boys. Let a be a probability of a woman to have one boy, and correspondingly, 1-a to have two boys. Suppose N is the total number of women in consideration. Suppose x is the probability of the first boy to be homosexual and y is the probability of the second boy to be homosexual. We assume that these probabilities are independent of each other.
Let us first estimate the total number of boys born. It will be aN + 2(1-a)N. The number of homosexuals that are born is expected to be xN + y(1-a)N. The probability of a random boy to be a homosexual is (x + y(1-a))/(2-a).
Let us see what happens with fertility. For a random boy (including both homosexual and non-homosexual boys), what is the average number of sons his mother has? It would be one son for aN boys who are from one-boy families and 2 sons for 2(1-a)N boys who are from two-brother families. Hence a mother of a random boy has on average 2 - a/(2-a) children.
Let's see what happens with homosexual boys. We have axN homosexual boys from one-brother families and (1-a)(x+y)N gay boys from two-brother families. Hence the average number of sons for their mothers is (axN + 2(1-a)(x+y)N)/(axN+(1-a)(x+y)N) = (ax + 2(1-a)(x+y))/(ax + (1-a)(x+y)) = 2 - ax/(x+y-ay). If we denote by r the ratio y/x, then the result will be 2 - a/(1 + (1-a)r). If r is more than 1, then mothers of gays are more fertile then average mothers. If we assume that y = 1.5x and a = .5, then the average number of sons for a mother of a random boy is 1.667 and for a homosexual boy, it is 1.714, a 3% increase. The impact will be stronger if we take into consideration three-boy families.
Now let us look at brothers in two-son families. There is a total of (1-a)N such families and they have a total of (x+y)(1-a)N gay boys. We have 2xy(1-a)N gay boys who live in families in which both brothers are gay. Hence, the probability of a gay boy who has a brother to have a gay brother is 2xy/(x+y). We saw earlier that the probability of a random person to be gay is: (x + y(1-a))/(2-a).
Let's look at these numbers more closely. You can easily see that if x = y these two probabilities are the same — as they should be. If x = 0 and y > 0, then a gay person never has a gay brother, suggesting negative correlations with a genetic component. Suppose y = rx, where r is a constant. Then the first number is 2rx/(1+r) and the second number is: x(1+r(1-a))/(2-a). We see that the ratio of these two numbers doesn't depend on x and is equal to 2r(2-a)/(1+r)(1+r-ar). Suppose r = 1.5, then the ratio is 2.4(2-a)/(5-3a). If a = .5, this ratio is 1.03. So, in this model, for a gay boy who has a brother, the probability that this brother will be gay is 3% higher than the probability that a random man will be gay.
I am so fascinated with the fact that a property that depends on the birth order can create an illusion of a genetic component. I am not discounting the possibility of a genetic component for male homosexuality, but I urge researchers to recalculate their proofs, adjusting for the impact of the fraternal birth order.
To be fair, the female fecundity correlation with male homosexuality was shown not only in mothers of gay men, but also in maternal aunts. Also, the increase in the probability of being gay for a brother of a gay man is very much higher than 3% in my model. That means these researches might survive my critique. Still, they ought to look at their numbers again.
Finally, this discussion is not really about homosexuality, but about any property that depends on birth order. In this case, such a property might imply a genetic component that doesn't really exist.


The Symmetries of Things by John H. Conway, Heidi Burgiel, and Chaim Goodman-Strauss is out. It is a beautiful edition with great pictures.
The first chapter is very nicely written and might be recommended to high school and undergraduate students. It covers symmetries of finite and infinite 2D objects.
The second chapter adds color to the theory. For beautiful colorful pictures with symmetry, there are two symmetry groups: the group that preserves the picture while ignoring its coloring and the group that preserves the picture while respecting its coloring. The latter group is a subgroup of a former group. This second chapter discusses all possible ways to symmetrically color a symmetric 2D picture. The chapter then continues with a discussion of group theory. This chapter is much more difficult to read than the first chapter, as it uses a lot of notations. The pictures are still beautiful, though.
The third chapter is even more difficult to read and the notations become even heavier. This chapter discusses hyperbolic groups and symmetries of objects in the hyperbolic space. Then the chapter moves into 3D and 4D. I guess that some parts of the second and the third chapters are not meant for light reading; they should be considered more as reference materials.
Here are pictures of a musnub cube (multiplied snub cube), built by John H. Conway. It is an infinite Archimedean polyhedron. The description of it is on page 338 and the diagram is on page 339 of the book. This object was glued together from stars and squares. Each corner of the square is glued to a point of one star and to an inside corner of another star. Mathematically, a star is not a regular polygon. If you look at stars with your mathematical eye, each star in the picture is not just a star, but rather the union of a regular hexagon with 6 regular triangles. That means the list of the face sizes around each vertex of a musnub cube officially is represented as 6.3.4.3.3.
The finished musnub cube picture shows a non-finished musnub cube. You can't really finish building an infinite structure. Right? It is finished in the sense that John Conway finished doing what he was planning to do: to construct a part of a musnub cube inside a regular triangular pyramid.
Did I mention that I like the pictures in The Symmetries of Things?
I am now a proud owner of a Zipcard. My old car died a horrible, screaming death recently and I decided to try to go carless as an experiment, hoping to save some money or to lose weight.
Zipcar is the modern way to rent a car. You reserve a car by the hour or by the day through the web, arrive at the site, swipe your card and drive away.
My biggest problem with being a Zipster is that the closest Zipcar location to my home is about one mile away. On second thought, I am losing weight.
But for other Zipsters, the biggest problem is that you have to return the car at the exact location where you picked it up. Obviously, if you allow renters to return their car to a different location the Zipcar company might run out of paid parking spaces in a particular location or, even worse, the cars might migrate to certain places, leaving other locations without any car.
I would like to propose an algorithm that will add some flexibility to where you can return a car, without overwhelming the system.
Here's how it would work. Suppose we have three cars currently assigned to the Mt Auburn/Homer Ave location. I suggest we name three as a desirable number, but actually allow from three to four cars to be assigned to this location at any particular time.
Now suppose I want to pick up a car at the Mt Auburn/Homer Ave location and to return it to the Somerville Ave/Beacon location. If the number of currently assigned cars to Mt Auburn/Homer Ave location is three (at the lower limit), the Zipcar reservation webpage tells me, "Sorry, you can't use this location unless you return your car back here," and shows me the closest location with extra cars. The same goes if the number of assigned cars at the Somerville Ave/Beacon location is at its upper limit. If my starting point has more cars assigned to it than its lowest limit and my destination point has fewer cars assigned to it than its upper limit, then I am allowed to take a car from my starting location and return it to my destination. Zipcar can throw in some financial incentives. If my choice disrupts the most desirable balance of car assignments, I have to pay a fee. If my choice restores the balance, I get a bonus discount.
It would be so cool if zipcars were flexible. I understand that the average cost to the company of parking each car might go up with my flexible algorithm as Zipcar will need more parking spaces than cars. But Zipcar can start implementing this flexibility with a small number of flexible locations. It would be a great feature.
Hey, Zipcar algorithm designers! Can I get a bonus if you implement my algorithm? I can also design a financial incentives formula for you.


I updated my funny pictures page with five new pictures. My new favorites are "Cape Cod Levitation Society" on the left and "Grilled Violators" on the right.
Here I repeat the Conway's Wizards Puzzle from a previous posting:
Last night I sat behind two wizards on a bus, and overheard the following:
— A: "I have a positive integral number of children, whose ages are positive integers, the sum of which is the number of this bus, while the product is my own age."
— B: "How interesting! Perhaps if you told me your age and the number of your children, I could work out their individual ages?"
— A: "No."
— B: "Aha! AT LAST I know how old you are!"Now what was the number of the bus?
It is obvious that the first wizard has more than two children. If he had one child then his/her age would be the number of the bus and it would be the same as the father's age. While it is unrealistic, in mathematics many strange things can happen. The important part is that if the wizard A had one child he couldn't have said 'No'. The same is true for two children: their age distribution is uniquely defined by the sum and the product of their ages.
Here is a generalization of this puzzle:
Last night I sat behind two wizards on a bus, and overheard the following:
— Wizard A: "I have a positive integral number of children, whose ages are positive integers, the sum of which is the number of this bus, while the product is my own age. Also, the sum of the squares of their ages is the number of dinosaurs in my collection."
— Wizard B: "How interesting! Perhaps if you told me your age, the number of your children, and the number of dinosaurs, I could work out your children's individual ages.
"
— Wizard A: "No."
— Wizard B: "Aha! AT LAST I know how old you are!"
Now what was the number of the bus?
As usual with generalizations, they are drifting far from real life. For this puzzle, you have to open up your mind. In Conway's original puzzle you do not need to assume that the wizard's age is in a particular range, but once you solve it, you see that his age makes sense. In this generalized puzzle, you should assume that wizards can live thousands of years, and keep their libido that whole time. Wizards might spend so much of their youth thinking, that they postpone starting their families for a long time. The wizards' wives are also generalized. They can produce children in great quantities and deliver multiple children at the same time in numbers exceeding the current world record.
Another difference with the original puzzle is that you can't solve this one without a computer.
You can continue to the next step of generalization and create another puzzle by adding the next symmetric polynomial on the ages of the children, for example, the sum of cubes. In this case, I do not know if the puzzle works: that is, if there is an "AHA" moment there. I invite you, mighty geeks, to try it. Please, send me the answer.
In case you are wondering why the wizard is collecting dinosaurs, I need to point out to you that John H. Conway is a superb puzzle inventor. His puzzle includes a notation suggestion: a for the wizard's age, b for the bus, c for the number of children. Hence, the dinosaurs.

Everyone agrees that you snore because some muscles at the back of your mouth are too relaxed when you sleep. Back in Russia, I heard about exercises for snorers that strengthen those muscles, but I never heard about them here. That is, until now.
Even medicine in this country is oriented towards making money. Simple exercises do not make much money. Here they offer you many devices and pills and even operations to relieve snoring, but not much in the way of exercise. Recently, though, I heard a very simple idea — sing before going to bed. Singing will help tone your throat muscles.
Some people are making money off of singing, too: check out the Singing for Snorers CD.
I was waiting for a train in Newark. On the platform, there was an LCD screen that flashed advertising. The ad I was staring at was titled, "Reasons to take NJ Transit to Prudential Center, #15." I was impressed that the NJ Transit sales people were working so hard to invent that many reasons.
I waited for my train for half an hour. It turned out that the NJ Transit advertising people were not working hard after all. The screen was flipping between four reasons, numbered 3, 6, 12 and 15. This is a case of false advertising. You look at reason number 15 and think that there must be a lot of reasons. They fool with your head. Cheaters.
I hope you noticed that I did the same thing with this posting — purely in order to illustrate my point.
Here is my simplified version of Conway's wizards puzzle.
Last night when I was coming home from my writing class with Sue Katz, I sat behind two wizards on the bus, and overheard the following:
— Wizard A: "I have a positive integral number of children, whose ages are positive integers, the sum of which is the number of this bus, while the product is the amount of dollars I have in my pocket."
At this point I interrupted the wizard. "Excuse me, professor, I overheard your conversation and can't resist asking you a question. Usually when a father says 'my children' everyone assumes that he has at least two children. Can I assume that?"
— Wizard A: "No. I stated my assumptions up front. A positive integral number of children means one or more."
I started thinking. If I were to explain this to a non-mathematician who assumes that 'my children' means more than one child, I would need to change the wizard's statement into the following:
"I have at least one child. The ages of my one-or-more children are all positive integers. The sum of the ages of my children or the age of my only child is the number of this bus. The product of the ages of my children or my only child's age is the amount of dollars I have in my pocket."
Hmm. I like that mathematicians use 'my children' to indicate any number of children. Makes puzzles faster to type.
Anyway, the wizards continued their discussion:
— Wizard B: "How interesting! Perhaps if you told me the number of your children, I could work out their individual ages"
— Wizard A: "No."
— Wizard B: "Aha! AT LAST I know how many children you have!"
If I were John Conway, I would have asked you next, "What is the number of the bus?" As I am not John Conway, I'll ask you, "Why do we presume that Wizard A hasn't cheated on his wife?"
The answer is that all wizards are notorious for making precise statements. If he cheats a lot, he would have started the conversation with, "The number of children I know about is a positive integer." Or maybe, more discreetly, "My wife and I have a positive integral number of children."
If you have already figured out the number of the bus, the bonus question is, "Why did I change the 'age of the first wizard' in Conway's original puzzle into the 'amount of dollars' in my puzzle?"
When I left the bus, I started wondering why on earth anyone would ever want to sum up the ages of their children. And I remembered that I once did it myself. I was trying to persuade my sister to apply for U.S. citizenship. My argument was that by moving here the life expectancy of her children would increase by 30 years. Indeed, she has two sons and the male life expectancy in Russia and the U.S. has an astonishing 15-year difference. I have to admit that my argument is not very clean, as we do not know the causes for this difference and, besides, the data is for life expectancy at birth and it changes while our kids age. My sister dismissed my argument, saying that the low male life expectancy in Russia is due to alcoholism and that her family is not in the high-risk group.
So, there could be a reason to sum up the ages of your children, but why would anyone ever want to multiply the ages of their children? In any case, if the first wizard continues to keep an amount of dollars equaling the product of the ages of his children in his pocket, his pocket will do better than mutual funds for the next several years.
I know I'm a computer addict, because:
If you're reading this, you might be as bad as I am. Please finish this sentence and add it to comments below: "I know I'm a computer addict, because …"
This puzzle was given to me by John H. Conway, and he heard it from someone else:
Find a ten-digit number with all distinct digits such that the string formed by the first k digits is divisible by k for any k ≤ 10.
Surprisingly, there is a unique solution to this puzzle. Can you find this very special ten-digit number?
For the contrast, consider ten-digit numbers with all distinct digits such that the string formed by the last k digits is divisible by k for any k ≤ 10. These numbers are not so special: there are 202 of them. My puzzle is: find the smallest not-so-special number.
John Conway sent me a puzzle about wizards, which he invented in the sixties. Here it is:
Last night I sat behind two wizards on a bus, and overheard the following:
— A: "I have a positive integral number of children, whose ages are positive integers, the sum of which is the number of this bus, while the product is my own age."
— B: "How interesting! Perhaps if you told me your age and the number of your children, I could work out their individual ages?"
— A: "No."
— B: "Aha! AT LAST I know how old you are!"
Now what was the number of the bus?
The first time I heard about the "stopping problem," many years ago, it was in this version: The king announces that it is time for his only daughter to marry. Shortly thereafter 100 suitors line up in a random order behind the castle walls. Each suitor is invited to the throne room in front of the eyes of the princess and the king. At this point, the princess has to either reject the suitor and send him away, or accept the suitor and marry him. If she doesn't accept anyone from the first 99, she must marry the last one. The princess is very greedy and wants to marry the richest suitor. The moment she sees the suitor she can estimate his wealth by his clothes and his gifts. What strategy should she use to maximize the probability of marrying the richest person?
The correct strategy is to reject the first 37 suitors and then marry the one who is better than anyone else before him. Generally, if there are N suitors the number of people to skip is about N/e — slightly more than one third of the whole group.
However, the greedy princess never received a good mathematical education. It is clear that her goal should have been to maximize the expected wealth of the future husband. In this case the strategy would be different; in particular, it changes significantly at the end. Let's imagine that when the line of leftover suitors thins, she realizes that she's already rejected the best one. In this case, it would be in her interest to consider the second best and, closer to the end, even the third best.
In real life, marrying the second best creates a burden of regret and bitterness. Let us assume that we all want to marry the best we can. But of course in our cases, the best does not necessarily mean the wealthiest. Also, we do not know how many suitors are lining up for us. Back in Russia I heard that a woman, on average, receives ten proposals. So, we should skip the first three, then marry the best person after that.
I do not know how many proposals an average American woman gets, but nowadays she doesn't have to wait for an official proposal before deciding whether a guy is right for her. The question becomes: which marriage candidate should a woman try to marry?
If we assume that marriage candidates are distributed evenly in time and girls are seriously hunting for husbands between ages 20 and 35, then the above math advice can be applied in the following way: From age 20 to about 25 or 26, just look around and see what life offers you. After that, marry the one who is better than all the previous ones.
This is a very mathematical piece of advice. The idea makes sense: first you sample your options then you target the best. The problem is that these assumptions do not cover our real-life situations. Let's look at some realistic adjustments and how they affect the age at which you stop sampling and become more active.
Based on the mathematics and discussion above, here is the advice I would give to my teenage daughter — if I had one:
Take your time looking around and sampling your boyfriends. Constantly analyze the pool of your boyfriends as a whole. If there are strange patterns — for example, all of them look exactly like your father or you always pay for their dinners — start psychotherapy and work it out. As soon as your boyfriends start to look different from each other — except for things that are important to you, like education — compare your dream husband to the pool. If you dream about a Nobel prize winner who is not older than 30 and on the list of the 100 sexiest men alive, you should adjust your expectations to your chances. You will choose a guy who is better than anyone before, but it is unrealistic to expect him to be much better. As soon as you get to a cut-off age, which you have estimated using the suggestions above, stop sampling and start deciding. As soon as you find someone who is better than anyone else before, go for it — marry him.
That was advice from my brain, now I will give you advice from my heart:
Use mathematics to guide you, but make the final decision with your heart.
I read an article published in US News and World Report: Alcohol in Teens Leads to Adult Woes. This article describes the discovery that teenagers who drink heavily are much more likely to become alcoholics and have mental disorders and depression when they become adults, and that they are much less likely to finish college or be satisfied with their jobs.
This correlation is not surprising. Have you ever seen a depressed alcoholic satisfied with his/her job?
For me, the interesting question is what the word "leads" in the title "Alcohol in Teens Leads to Adult Woes" means. One might interpret "leads" as indicating that alcohol in teens causes the adult woes. If we persuade our teenagers to abstain from alcohol, will they have fewer problems in their adult lives? Will it help if you install pictures of a cirrhotic liver as a screen saver for your child's computer?
In the middle of the article, there is a sentence that correctly states:
"What these data don't tell us is whether those kids were already predisposed to have problems or whether drinking helped cause the trouble."
Who is the genius who came up with a title that contradicts the article? Did they even read the article? Flashy titles sell better, but such contradictions show disrespect to the reader.
The truth is that correlations are usually insufficient to prove causality; a different type of research is needed. It appears that some of it was actually done. An interesting article, "A longitudinal study of alcohol use and antisocial behaviour in young people," describes the study that investigated the causality between alcohol and woes. In this study, they started with three hypotheses about the long-term causality:
I didn't check this study, but the fact that they are trying to compare different hypotheses is encouraging. The result of this study is that the data supports the second hypothesis &mdash in the long run, antisocial behavior causes alcohol use. That means the correct title for the article in the US News and World Report should have been: "Teen Woes Lead to Adult Alcohol."
So what can you do to stop your teen's antisocial behavior? There are many studies on that subject too. I do not know if they are correct, but you might consider a fish diet for your teen or sign up your child to train dogs.
My English teacher and editor Sue Katz wrote a funny blog entry about masturbation: "Sex and the Single Hand: Stroke Your Way to Health"
I followed the link of one of the studies she mentions to the BBC article "Masturbation 'cuts cancer risk'", where " … They found those who had ejaculated the most between the ages of 20 and 50 were the least likely to develop the [prostate] cancer."
When I hear such results, my first question is, "How was the study conducted?" It appears that "Australian researchers questioned over 1,000 men who had developed prostate cancer and 1,250 who had not about their [past] sexual habits." The problem with asking people about their sexual habits 30 years ago is that there are a large number of dead people you can't ask. What if the most active masturbators have died from fatigue?
Should you masturbate more to reduce your cancer risk as the BBC suggests?
Prostate cancer might not be related to masturbation at all, but rather to something else that correlates with masturbation.
In case you are wondering how one's Internet connection is related to all this, let me remind you of a joke about a conversation between two geeks.
— "When you look at a girl, what do you notice first?"
— "Her hair, then her eyes, then her nose, then her lips — I have dial-up."
One thing I know for sure: women who masturbate have even less prostate cancer than men who masturbate. Hooray for masturbation!
The smallest positive index m such that the Fibonacci number Fm is divisible by the number p is called the rank of apparition of p. If p is prime, one can prove that any Fibonacci number that is divisible by p has an index divisible by m.
Even Fibonaccis have indices divisible by 3. That means that if for some p the rank of apparition of p is divisible by three, all the Fibonaccis that are divisible by p are even. Therefore, no odd Fibonacci divides p. I already discussed this subject in my previous post "9 Divided no Odd Fibonacci."
Now let's look more closely at the set of primes that divide no odd Fibonacci. The Fibonacci numbers obey the following identity: Fn+k = (1/2)(FnLk + FkLn), where Ln are Lucas numbers. From here F3n = (1/2)Fn(L2n + Ln2). Like Fibonacci numbers, exactly every third Lucas number is even. Hence, the parity of L2n is the same as the parity of Ln. Hence, L2n + Ln2 is divisible by 2. Let us denote Gn = (1/2)(L2n + Ln2).
As we have already discussed before, if no odd Fibonacci is divisible by p, p's rank of apparition is of the form 3n which means p divides F3n and doesn't divide Fn. Hence, p divides Gn. On the other hand, we can show that Gn = 5Fn2 + 3(-1)n. Hence, the only common divisor that Fn and Gn can have is 3. Let us take any prime divisor s of Gn other than 3. We see that F3n is divisible by s while Fn is not. The rank of apparition of s must be a divisor of 3n and not a divisor of n. Hence this rank is divisible by 3. Thus we can see that with the exception of 3, the set of prime divisors of elements of Gn is the set of primes that do not divide odd Fibonaccis.
Here's a bit more info about the sequence Gn. It is sequence A047946 in the Online Encyclopedia of Integer Sequences. It is a recurrence: Gn=2*Gn-1+2*Gn-2-Gn-3. Thus, we have found a recursive sequence, elements of which have a set of prime divisors which with the exception of 3 is the set of primes that do not divide odd Fibonacci numbers.
Have you ever carried your mail from your mailbox directly to your recycle bin? If so, you feel my frustration with all this wasted paper. Each time I carry these catalogues up the stairs I think that my house should have a recycle bin next to my mailbox. Even better, maybe I can put my recycle bin at the post office, so my mailman doesn't need to carry all this weight around. The real solution would be to call the catalog company and ask them not to send any more catalogs. For a long time the idea of being put on hold for a long time and the uncertainty of success, not to mention my usual laziness, prevented me from doing this.
You might imagine how high I jumped with joy when I heard about Catalog Choice at http://www.catalogchoice.org, the company that will request on my behalf a cessation of these mailings. Their website is nicely done and appropriately greenish. You just register and enter the catalogs you do not want. It doesn't take much time and all the negotiation is done for you.
Up to this point, I've rejected 58 catalogs through this website. Only eight of them confirmed that they will honor my request. I even received a special confirmation letter from L.L.Bean. Sending a letter might be polite, but it contradicts my goal of reducing the waste of paper and of my time.
Unfortunately, there were three catalogs, including Newport News, that refused to honor my request. I was so angry that I decided to call Newport News and demand my removal from their mailing list. They agreed to my request. Can you guess what happened next? I received another catalog. I called them again. And I was removed from the list again. I received yet another catalog. I called them again. They told me that I am in their database marked as a person to whom they shouldn't send catalogs. But the catalog they sent to me had a temporary customer number, so it is not in their system and therefore doesn't count. According to Newport News' logic, the check-mark in the database indicating that I am not supposed to receive catalogs supersedes the fact that I actually continue receiving them. They believe their database is more reliable than facts. What can I do? I will not buy from Newport News again.
Later, I made another interesting observation: I started receiving catalogs with my name misspelled. Do they really think that if they write Tonya instead of Tanya, I will suddenly become interested in their catalogs? We all know that the reason of the misspelling is so that they can pretend to honor my request, but still send me their catalog.
This situation is not right. I shouldn't be getting catalogs against my will, especially after I've made my preferences clear. I think that we should fine companies that persist in doing this. Perhaps we can have a "Do Not Mail Me Catalogs" Registry that is similar to the government's "Do Not Call" Registry.
Meanwhile, if you are like me and care about the environment, you too can sign up at the Catalog Choice.
I was very proud of myself when I started receiving tons of comments for my math blog. Many of the comments were quite flattering. For example:
You are getting better and better. Congrats, dude.
I know that in English you can sometimes replace "ladies" with "guys", but I wasn't sure if being called a dude constitutes a compliment.
I got suspicious, however, when I received this:
Get real! It is interesting, but you never give proofs.
This comment was placed on my Fibonacci entry, where I think I gave more than enough proofs. So I read all the small print that accompanied the comment. It appears that "sexy-girls-in-chains" were extremely excited about the divisibility of Fibonacci numbers.
I am used to my everyday winnings of Millions of Dollars in the UK lottery, but this was something new and different. They caught me off-guard. Here I was, so proud of the public's positive reactions, only to realize that it was some automated program. Some computer sending spam caused me to have strong emotions. I was upset that I was caught. Sigh.
What can I do? Just laugh. We can laugh together at "girls-deflowered" who were interested in Quantifying Favors, at "is-your-penis-small" who commented on Losing the Lottery, at "squirting-vibrating-realistic-anal-dildo" who was impressed with my Fantasy Future and at "teenage-girls" who associated themselves with Numbers Needing Sponsors.
One of the latest comments was:
We can professionally say that this information is objective and true and of highest quality.
It was signed by "pissing-ladies." Am I proud or what?
Here are recent additions to my math jokes collection:
* * *
During a lecture to his students, a military instructor says, "There is a 40% chance that we will hit our target."
One student asks, "What happens if we aim away from the target?"
The instructor replies, "Logically, we would have a 60% chance of hitting the target."
* * *
"Do you know that 67% of people are not capable of doing simple arithmetic?"
"I belong to the other 23%."
* * *
What is so special about 6.9?
It is 69 ruined by a period.
* * * (submitted by Irene Ogievetskaya)
Teacher: Solve the equation: x + x + x = 9.
Student: x = 3, 3, and 3.
* * *
Teacher: What is 2k + k?
Student: 3000!
I stumbled upon an article in the Boston Globe (February 29, 2008) titled "Study: Spanking children affects their sex lives as adults." Here are some quotes:
New research by a University of New Hampshire domestic abuse expert says spanking children affects their sex lives as adults. …[C]hildren who are spanked are more likely as adults to coerce partners to have sex, to have unprotected sex and to have masochistic sex.
The classical method to prove scientifically that spanking affects something is to find many parents of newborn identical twins and persuade them to treat their children the same way, with the exception that they spank one and do not spank the other. The researchers should then compare these twins in their adulthood. Such a project is impossible, as parents are likely to start feeling guilty towards the child they spank, for you can't separate spanking from the whole package of how parents treat their children.
I decided to study the study. I found a more detailed description of the study in the Concord Monitor. As I suspected, the study was a survey. The survey found a correlation between spanking and "undesirable" sexual behavior. As every statistician knows, correlation doesn't prove causality.
Here's another quote from the study: "The best-kept secret in child psychology is that children who were never spanked are among the best behaved." Did it occur to anyone that the best behaved children do not need spanking?
Could it be that parents who spank their children are tired, impatient and less loving? Could it be that not being loved as a child affects your sexual behaviour as an adult much more than spanking?
Could it be that parents who spank their children are more aggressive in general? Could it be that they pass their aggressive genes to kids and their kids' aggressive behavior is related not only to upbringing, but to genetics?
Do not get me wrong. I do think that spanking is bad. I am saying that the study doesn't prove that spanking is affecting anyone's future sex life.
I am surprised that so many magazines republished the article without thinking. Now all the country is fooled into believing that the easy way to improve their kids' future sex life is to stop spanking.
Go ahead! Stop spanking. Love your children too.
I tried to enroll on a website recently, but they didn't allow me to continue without choosing five security questions out of about ten samples they supplied. I started in good faith to do what they asked.
Question: What is your father's middle name?
Answer: They do not have middle names in Russia; they have something called "otchestvo" and I know seven different ways to spell my father's.
Question: What is the name of the street on which you were born?
Answer: I am glad it was not Lenin Street, but it was equally bad. Besides, it was renamed and I am not sure which name to choose.
Question: What is the name of your high school?
Answer: Finally, an easy question. In Russia we didn't have names, but rather numbers for schools. I happily entered 444, and oops — the applet wouldn't accept numbers.
I couldn't find five questions that I could answer uniquely and reliably. I felt that the designers of these questions were clueless and disrespectful to other cultures. Then I thought about whether I really wanted some creepy database to know the name of my best friend. No, I didn't.
Now I have established a file where I put the answers to security questions and I can have all the fun I want with my new biography. I can name my first dog Tom Cruise and have my wedding date be 20 years before I was born. I can name my husband Freedom Of Speech and my city of birth IHateSecurityQuestions. Maybe next time I will switch: Freedom Of Speech will be my dog and Tom Cruise my husband.
If you are lazy like me, you can choose your questions so you have the same answer for everything. This way you do not need to type much into your file. For example, you can name your city, your cat and your best friend George Washington. Or, if you are really lazy, God.
I just read the following in Women's Health Magazine (March, 2008; page 54): Visa conducted a study of 100,000 fast food restaurant transactions. They found that people who pay with credit cards spend 30% more on food than people who pay cash.
The article concludes with the suggestion to pay cash, so you spend less and lose weight.
My question is: Who is more incompetent, Visa or Women's Health Magazine?
Perhaps people who do not have credit cards are poorer and more price-conscious; hence, they spend less on food. This might explain the correlation. Here's another possible explanation: people who are ordering for large groups might prefer to pay with a credit card. Or, maybe stores do not like using credit cards for small transactions, so they encourage people to pay cash for modest orders.
The main rule of statistics is that correlation doesn't mean causality.
There are several possible answers to my question about incompetence:
It could well be that paying cash makes you stingier, or at least more price-conscious, but I can't trust Women's Health Magazine any more. One thing I know for sure is that math can help you lose weight. Math allows you to differentiate a good study from a dumb study.
Recently I was buying gas at a gas station. I was paying with my credit card and the machine asked for my zip code. If you read my previous post, you know what happened: I got furious. First, I tried 00000 as a zip code. The machine was smart enough to tell me that it was invalid. No matter what combination I tried, it wouldn't accept another zip code.
Finally, the machine got frustrated with me and printed on its screen that I needed to talk to the cashier. Then, I argued with the cashier. He could have suggested that I pay cash, but he didn't. I left without gas.
Luckily, for me I had dinner that day with my son, Alexey Radul, and his friend, Grem. Grem explained to me that gas stations are not collecting customers' zip codes. They use zip codes as a security measure for checking that the credit card is not stolen. I guess that means I behaved exactly like a person who stole a card. Protecting your own privacy sometimes makes you look like a thief.
After dinner, I went back to the same gas station to conduct some experiments. This time I was armed with several valid zip codes. It didn't work. Grem was right — only the zip code corresponding to the card could have worked. I looked like a thief again. I paid for my gas with cash and left.
The next day I called my credit card company and asked them about this. The manager I talked to told me the same thing as the manager Grem talked to. Apparently credit cards do not give your zip code information to gas stations. Your zip code is used instead of a pin number to verify that your credit card is not stolen. So in this case you do not need to worry that you are providing extra information, since credit card companies know your zip code anyway.
Nowadays, supporting a database is cheap. Computer storage is cheap, too. This gives companies an opportunity to collect more and more information about us. If you think, as I do, that this is an invasion of your privacy, here are some ways to resist.
When you buy something over the Internet or through a catalog, they ask for both your email address and telephone number. They may need a way to contact you in case something happens with your order, but they do not need both. When you are ordering online and their default contact is by email, they do not need your phone number. If the website requires your phone number, you can put in a fake number. Of course, you are a nice person and do not want to provide some innocent soul's phone number instead of yours. Here is the perfect solution. Put the number 555-5555 as your home number with any area code.
The phone numbers of the format 555-xxxx are reserved for the movie industry. That is, if Hugh Grant calls Julia Roberts in a movie, there would be hundreds of bored or not very smart people who would try to call the same number Hugh dialed hoping to talk to Julia Roberts. For these situations, the movie industry reserves all the numbers of the form 555-xxxx. This way they guarantee that all of these fans will not bother a real person. So you can use these numbers without any guilt.
If you are ordering by phone, they might see your number on the caller ID. In this case, you can always say that you do not have an email address. You can also use a one-time email address offered through Sneakmail or AddressGuard at Yahoo.
Store shopping cards also scare me very much. When you use your store shopping card, they know exactly what and when and in what amounts you are buying. If you do not want anyone to know that you are buying 100 Tylenol pills a month, do not use your store card, and consider paying cash.
My friend Sam Steingold suggested I try card swapping. You have a CVS card and your friend has a CVS card — you can swap them. CVS's database will register that you quit buying Tylenol in Boston, but started buying cigarettes in Atlanta. If you continue swapping, CVS's database will be totally confused. The good part of this idea is that if someone tries to hold your purchases against you, you have a way to prove that you are not responsible.
The disadvantage of card swapping, is that for the transition time you lose targeted coupons. Your friend in Atlanta will get all the Tylenol coupons he doesn't need. But you still will be able to buy sale items with discounts.
Here's what I did - I put another last name on my CVS card. They didn't notice. If they were to notice, I would have told them that I am in process of changing my last name to my newly acquired husband's last name and would ask for newlyweds' coupons.
Sometimes when you buy things, they ask you for your phone number at the cash register. It is even worse than shopping cards. They have your information on file without giving you your discounts. Just remember: you can always refuse. Or if you're not comfortable refusing, let us all agree to give the same number: (area code)-555-5555. Let their analysts wonder why the same person is buying morning-sickness pills in one store and condoms in another.
My Number Gossip page is on hold. I am out of work and can only afford to spend time on things that can bring me my next job. As a result, numbers suffer. If you would like to support the website, consider donating to Number Gossip. With your donations, I will be able to spend more time on the website. There are many things I would like to do. Here are the three most important and fun areas that I would chose to work on.
I've devoted many years to this project, and now I need some financial help. If you know a person or a company who wants to sponsor numbers, please ask them to contact me at (tanyakh at yahoo).
Alice and Bob are good friends. Bob caught a cold and called Alice for help. He wanted Alice to go to a pharmacy and bring him some cold medicine. Alice did that and I would like to assign a number to this act of giving. How can we quantify this favor?
First, we need to choose a scale. Usually favors cost us in time, money and emotions. Alice spent half an hour driving around, plus $5 on the medicine (we'll skip the cost of gas for simplicity). It also cost her emotionally, especially because the traffic was really bad.
Measuring everything on three scales is complicated. I would like to convert everything to one scale, because in the future I intend to compare this act of giving to other favors Alice does. For example, Alice knows for sure that this favor for Bob was a less costly favor than her phone call yesterday to her ex-mother-in-law, even though the phone call took only five minutes and didn't cost any money.
We probably can convert everything to dollars, but I am trying to resist this money-driven society that measures everything in dollars. So, I prefer to use points. Each dollar translates to one point, but time and emotion are more subjective.
Alice makes two calculations in her head: what she really spent and what she is owed.
Here's what she spent: Alice counts 5 points for the medicine. She also views her time as money. She charges $100 an hour for consulting and values all her time at this rate. Hence, she adds 50 points for time spent. Traffic was bad, but not so bad. She thinks that her traffic stress cost her 15 points. Since she also had to cancel her date with her boyfriend, she estimates her annoyance with this at 100 points. On the other hand, she got this warm feeling from helping Bob and she was happy to see him. So she thinks that she got back 30 points. Adding all this up, we get a total of 140 points. This is how much Alice thinks she spent for this particular favor.
Does it mean that Alice thinks that Bob owes her 140 points? Usually not. The calculation of how much Alice thinks Bob actually owes her is completely different. She thinks that he owes her 5 points for the cost of medicine. Also, she knows that Bob earns much less than she does and values time differently, so she think that he owes her 30 points for her time. Since Bob is not responsible for traffic, she doesn't add traffic points. Also, she never told Bob that she had to sacrifice her date for him, so she doesn't think it's fair to want Bob to be thankful for the sacrifice he doesn't know about. At the same time she hopes that one day Bob will sacrifice something for her. She can't ignore this sacrifice completely, so she adds 10 points for that. Altogether she thinks that Bob owes her 45 points.
Do you think Bob feels as if he owes Alice 45 points? Like Alice, he also has two numbers in his mind. One number is the amount of points he received as a result of this favor and the other number is how many points he officially owes Alice.
He actually was planning to ask his neighbor to buy the medicine, but for some reason he called Alice first and she offered help. Alice was delayed at her work and arrived at Bob's place much later than he expected. She also brought the worst flavor of the syrup. Bob doesn't value time as much as Alice, so he thinks that Alice spent 10 points driving and 5 points on the medicine. Bob felt ill throughout Alice's visit and did not enjoy seeing her. Combining that with her late arrival with the wrong syrup, he thinks that he was annoyed for about 15 points. So he thinks that he got zero points from this transaction.
At the same time he wants to be fair. Bob knows that Alice did her best to help him; besides he never specified the flavor he likes. As a result, he doesn't count his annoyance in how much he owes Alice. So he thinks that he owes Alice 15 points. What Bob really did to thank Alice, I will discuss in a later blog entry.
In conclusion, let me remind you of my system. I measure all favors in points. And for each favor I assign four numbers:
My favorite puzzle at 2008 MIT Mystery Hunt was the puzzle named Functions. Here is this puzzle:
36 -> 18 A,B 2 -> 1 A,C,G,H,K,L,O 512 -> 256 A,C,H 4 -> 2 A,G,H,Q 320 -> 160 A,R 411 -> 4 B,E,Q 13 -> 3 B,G,K 88 -> 11 C,D 45 -> 9 C,D,F,J,L 48 -> 6 C,G,M,P,Q 4 -> 1 C,K,L,N,O 36 -> 9 D,E,F 66 -> 8 D,E,G,I 10 -> 3 D,G,L 1 -> 3 D,L 150 -> 15 D,M 3 -> 2 E,H,J,K 25 -> 3 E,K,L,N,Q 9477 -> 14 E,M 129 -> 4 E,N,P 55 -> 10 F,J 411 -> 6 F,K,L,M,N 2002 -> 4 F,O,Q 79 -> 8 G,I,L,P 25 -> 20 H,M 176 -> 80 H,R 3665 -> 8 I,N,Q 7 -> 3 K,Q 11 -> 5 L,M 501 -> 2 L,O,P,Q 8190 -> 5 M,O 180 -> 3 O,P 50 -> 10 R ? -> (?) F,R (?) -> ? J,L (?) -> ? A,F (?) -> ? N,O,Q ? -> (?) A,D,J (?) -> ? D,H (?) -> ? G,K,Q ? -> (?) B,D,M (?) -> ? E,H ? -> (?) D,F,G,L ? -> (?) C,G,P
I had a dream that sometime in the future I am babysitting my two-year old granddaughter-to-be Inna.
Me: Here is one apple; here is another apple. How many apples will you get when we put them together?
Inna: Two.
Me: So, 1+1 is… ?
Inna: Two.
Me: Good girl.
Inna: How much is 2+2?
Me: Shhh. We can't talk about that.
Inna: Why? Will a big bad wolf come and eat us?
Me: Sort of. It is copyrighted and I do not have enough money for the private use license.
Inna: Did you spend all your money on a 1+1 license?
Me: No, honey. Google owns the rights and they released it for public use.
Inna: What about 3+3?
Me: We might be able to talk about it in a couple of years. The government is discussing the purchase of the rights, though it would be half of their annual education budget.
Inna: What about 4+4?
Me: 4+4 is approximately 8.
Inna: Don't you know if it is 8? Do you think it could be 7?
Me: No, I know exactly how much it is. But the copyright has a loophole. You can't say the exact sentence, but it doesn't forbid variations. Have you heard that Stephen Colbert is being sued for saying how much 4+4 is on his show? Colbert argues that his grimace constitutes a complete reverse in meaning.
Inna: What about 5+5?
Me: Your father's brother's nephew's cousin's former roommate is a lawyer and he says that the 5+5 license doesn't permit the answer to be in the same sentence as the statement. So, to be on the safe side, you should always go like this: "5+5 is a number. I like ice cream. My favorite flavor is chocolate. The number I've mentioned several sentences ago is 10."
Inna: Can this lawyer find a loophole in the 2+2 license?
Me: The copyright agreement itself is copyrighted and too expensive for him.
Later my son, Alexey, comes to pick up his daughter. I continue the conversation with him.
Me: Your daughter is gifted in math. Is there any chance that her public school can teach her how to add 10+10?
Alexey: I know that our public school bought a limited license. They can discuss additions only in a designated room on Mondays from 11:00am to noon and only after 8th grade.
Me: Why the heck wait until 8th grade?
Alexey: They are required to study copyright laws first and pass the state exams.
Me: Have you considered private schools? Inna is so gifted — she might even get a scholarship.
Alexey: Our private school was able to copyright only three questions for their scholarship evaluations. And everyone knows that the answers are A, D and D.
Me: I have an idea. I am subscribed to Russian TV. They have a channel that broadcasts an educational math show in English.
Alexey: How could that be? The U.S. blocks all foreign non-copyrighted broadcasts in English.
Me: Their English is so bad, everyone thinks it is French.
Alexey: Ah, I was wondering where my boss's son got his new horrifying accent.
At Inna's next visit, Inna came up with some ideas.
Inna (in a low voice): I think I know how much 2+2 is.
Me: You can't tell me that. But maybe you have a new favorite number. You can tell me your favorite number.
Inna: My favorite number is 4.
Me: Do you know how much 3+3 is?
Inna: I changed my mind. My new favorite number is 6 now.
Me: Good girl.
Inna: How come we are talking about addition and you never told me what the number after 10 is?
Me: Shhh. We can't talk about that… —
This is my first non-mathematical entry. But I invented this diet myself two days ago and I wanted to share it with you. It is a variation on my son Alexey's "Am I hungry?" diet.
The only restriction for my diet is that you are not allowed to eat while your brain is busy with something else, like watching TV or playing sudoku.
If you are driving to your office while reading a newspaper and talking on the phone, you are allowed to have your morning donut, but only if you stop the car and put away your newspaper and phone. This diet is based on having an undistracted dialogue with your food.
Here how this diet works. Each time you open your mouth to take a bite, you should look at your food and ask yourself, "Why the heck do I need this bite?" This is it. Just look and ask. Nothing more.
It is better if you say it aloud. But if you are on a first date you are allowed to pronounce it in your head.
Here is what happened to my cake yesterday. On the first "Why the heck do I need this piece of cake?" I just ate one bite. On the second "Why the heck do I need this piece of cake?" my inner voice told me, "Shut up. I just want it." On the third "Why the heck do I need this piece of cake?" my inner voice said: "Well, I am stressed out and I really crave some sugar. Besides, today is my last day at work, so I am allowed to celebrate." On the fourth "Why the heck do I need this piece of cake?" I just put the piece of cake back in the fridge. I didn't want it anymore. Altogether, I ate a third of my usual portion of cake. It works.
Try it. This diet is free. It is easy to remember. You do not need to change your lifestyle, go to the store to buy fresh vegetables or adopt new recipes. It might increase your morning commute time by one minute. But you can recover this minute by cutting down on exercise, since you won't need it quite as much.
There is a big difference between evaluating exercise DVDs and reviewing movies. You are supposed to use exercise DVDs many times. So the value of the DVD changes over time. An exercise DVD that is too difficult at the first try could become a lot of fun later. Alternatively, one that explains everything in detail can be great at the beginning, but it will become boring after several viewings.
Smart DVD producers probably know some common rules. The number of people who use a DVD for the first time is much bigger than the number of people who use it for the hundredth time. Users often post reviews and ratings of products they have bought. Therefore, the proportion of reviews by the first-time watchers is much higher than by the hundredth-time watchers. This means that to get better ratings the DVD producers should target the first-time watchers. Is this why we have so many boring exercise DVDs?
In my opinion, exercise DVDs should have two parts. One part explains everything by breaking the routine down into elements and the other part allows people who have learned the routine to do it without interruption.
Keep your eyes open for my upcoming web page with reviews of dance exercise DVDs that I own. These reviews will address both first-time users and every-day-for-a-year users.
Everyone knows that math education in public schools in this country is pathetic. If you looked at this problem from an economics point of view, the first question would be, "Qui prodest?."
Who profits from bad math education? I know one place — the lottery. People who understand how the lottery works rarely buy tickets. They might buy an occasional ticket as entertainment, but never as an investment. No wonder they say that the lottery is a tax on people bad at math.
Huge money from lotteries goes to states and towns, and a big portion of that goes to education. That means towns, schools and math teachers have direct financial incentive not to provide good math education. This conflict of interest creates a situation in which, in the long run, it is profitable for schools to hire very poor math teachers or cut their math programs.
The situation is unethical. I think that lottery organizers should at least pretend that they are resolving this conflict and spend part of the lottery money to educate people not to play the lottery.
I did it. I handed in my resignation letter to my boss. I'm resigning effective Jan 3, 2008. If you want to know why I'm waiting until next year, I can give you several reasons.
I am happy and sad at the same time. In four and a half years I've made a lot of friends and accomplished a lot professionally. Now it is my time to move forward. Where is forward? It is in the direction of a cemetery, but I would rather be doing something more meaningful to me than battle management while I am slowly crawling there.
Do you know that 1210 is the smallest autobiographical number? You probably do not know what an autobiographical number is. You are right if you think that such a number should be a pompous self-centered number whose only purpose in life is to describe itself.
Here is the formal definition. An autobiographical number is a number N such that the first digit of N counts how many zeroes are in N, the second digit counts how many ones are in N and so on. In our example, 1210 has 1 zero, 2 ones, 1 two and 0 threes.
Let us find all autobiographical numbers using the "zoom-in" method.
Now we continue zooming in in three different directions depending on the number of ones. In this blog entry, I will consider only the case in which there are no ones; I leave the other two cases to the reader.
Here is the full set of autobiographical numbers: 1210, 2020, 21200, 3211000, 42101000, 521001000, 6210001000.
This is the sequence A104786 in the Online Encyclopedia of Integer Sequences (OEIS), where I first encountered the autobiographical numbers.
Autobiographical numbers are very cute numbers. But there is a problem with their name. If there is a notion of an autobiography of a number, then it would be logical to expect that there is a notion of a biography of a number. What would be the logical candidate for a biography of a number? Let us say that given a number N, its biography is another number M such that the first digit of M is the number of zeroes in N, the second digit of M is the number of ones in N and so on.
Of course, for a number to have a biography, we need to assume that none of its digit is present more than nine times. Still there are several problems with the definition of a biography.
The first problem is that if N doesn't have zeroes, its biography starts with a zero. As numbers don't start with 0, that biography is not a number! Furthermore, if N starts with 0, it can have a biography but N is not a number. Luckily for this article, a digit string starting with zeroes can't be an autobiographical string, because the number of zeroes is not a zero. It is a relief that those illegitimate strings that are trying to pretend to be numbers can't actually be autobiographical.
The second problem with biographies is that a number can have many biographies. Indeed, if a number doesn't have nines, you can remove or add zeroes at the end of a biography to get another biography of the same number. Since mathematicians like to define things uniquely, we might consider it a problem if a number has several biographies. In real life it is possible to have many biographies of a person. So the second problem is not a big problem. I will call the shortest possible biography of a number the curriculum vitae and the longest possible biography the complete life story.
The third problem is that numbers with the same digits in different permutations have the same biographies. So in a sense a biography follows the life not of a number, but rather the set of its digits.
Suppose for now we allow a biography to start with 0. Also, let us choose the curriculum vitae — the shortest biography in case there could be several. Let us build a sequence of CVs. As an example, we start with 0. Zero's CV is 1, one's CV is 01, continuing that we get the following sequence: 0, 1, 01, 11, 02, 101, 12, 011, 12, 011, 12, …. You can see that the CVs' sequence fell into a cycle in this case. I tried sequences of CVs starting with many numbers. I found that they fall into two cycles. One cycle is described above and another one is: 22, 002, 201, 111, 03, 1001, 22. Can you find another cycle or, alternatively, can you prove that all the numbers that allow the sequence of CVs converge to only these two cycles?
Let us build the sequence of complete biographies, that is, life stories, starting with 0: 0, 1000000000, 9100000000, 8100000001, 7200000010, 7110000100, 6300000100, 7101001000, 6300000100, …. We see that this sequence falls into a cycle of length two. The members of this cycle are legitimate numbers. These numbers are too shy to advertise themselves. But Alice praises Bob, because Bob praises Alice. It's a very advantageous flattery pattern! I will call such a pair a mutually-praising pair. We've already seen mutually-praising strings: 12 and 001. Two other examples of number pairs thriving on each others' compliments are, first, 130 and 1101, and second, 2210 and 11200.
I would like to become a professor of mathematics. How can I get to academia? I was told that applicants are measured by the number of papers they write. They expect about 3 papers per year starting after the Ph.D. I got my Ph.D. 20 years ago. I published 6 papers after my Ph.D. papers. That means I urgently need to come up with 54 papers.
There are several problems with working in industry and trying to publish at the same time:
Because of these obstacles, the papers I have started at my job are on hold. It's unlikely that I'd be allowed to finish them during work hours.
So I started writing non-job-related papers on my weekends. I started doing this seriously a year ago. It goes very slowly and I hope to publish three papers soon, but my speed needs to be much higher than that to catch up with the 54 papers I didn't have time to write while being a single mom and providing for my family.
So, I came up with this idea: to quit my job and write papers. I do not have enough money to support this idea for very long. Certainly, not enough time for 54 papers. We probably can survive on my savings for half a year. My goal is to write as many papers as I can in half a year and see what my real speed is. This way I can at least prove to myself that I am a mathematician for real.
The only problem is that my savings were meant for a down payment on my first house. I've been asking myself for awhile: What is more important− a dream job or a dream house? I just realized today that I will never be happy if I am not happy at my job and I am quite happy with the apartment I am renting now. I guess this is it − I just have to take the plunge.
Are you afraid of Friday the 13th? Here is my only Friday the 13th story.
It was Friday the 13th and I was listening to the psychologist Joy Browne's show. Joy asked her listeners to call in with stories of interesting things that happened to them on Friday the 13th. I wondered why I didn't remember any stories about Friday the 13th.
At the end of her show, I went to pick up my mail, where I found a book kindly sent to me by Princeton University Press named Nonplussed!: Mathematical Proof of Implausible Ideas by Julian Havil. I opened this book to a random page and it was Chapter 13. That was not such a big deal by itself, but in addition Chapter 13 was titled "Friday the 13th".
One of the things Julian Havil discussed in the chapter is how often the 13th of the month falls on different days of the week. You might remember from your elementary school education that the Gregorian calendar repeats an entire identical day-of-the-week cycle every 400 years. Hence, it is just a matter of calculation to check on which day of the week the 13th falls the most often.
Can you guess the answer? I am sure you can apply some meta-thinking and derive that there is one special day of the week on which the 13th most frequently falls. You might even guess by now that that day is Friday. Otherwise, why would I write this blog entry? Or what would Mr. Havil have to say in the whole chapter of the aforementioned book?
As we can see, this calculation increases the worry for people who suffer from paraskevidekatriaphobia — the fear of Friday the 13th. The 13th falls on Friday more often than on any other day.
Should we be worried?
Mathematically, the difference between the number of Fridays the 13th and, say, Thursdays the 13th is so small that it can only be observed when we look at the 400 year lifetime of the Gregorian calendar. Many countries have yet to experience the full cycle of the Gregorian calendar. For example, Russia adopted the calendar only in the 20th century. Is this why I am not so very afraid?
On second thought, for people of my generation, who are unlikely to live until the year 2100, the situation is slightly different. In the years between 1901 and 2099 our calendar has a days-of-the-week cycle of 28 years. You can calculate and check that in the period of 28 years, the 13th falls on any day of the week with the same probability. Hence, in events happening around my life time, there is not much to worry about, because Friday is no more special than any other day.
On third thought, a particular individual might see more Fridays on the 13th in his lifetime depending on the exact date of his birth. In my own life up to today, Monday is the most frequently occurring 13th. Maybe that's why I do not like Mondays.
For 25 years my children were my priority. I made several decisions in my life that benefited my family, but "harmed" my mathematical career. I do not regret any of my choices. After all, being a single mom made me a more confident, stronger person. Maybe this will help my career in a long run.
Now that my youngest son is 16 years old, my life can't revolve around him anymore. Now I must think about the meaning of my life, beyond bringing up children. The only thing I want to do is mathematics. I am actually doing some math on weekends, but I really want to do it full-time. My tasks at my job are getting further and further from mathematics and research. In short, I feel that my job doesn't fit me at this stage of my life.
I really should find another job. I am somewhat scared of change though. I think that the first thing to do is to try to turn around the situation at my current job. There is a lot of interesting mathematics in battle management. The problem is to match a math problem to a charge number. That is, I would need to convince my management that the algorithms we design need a sound mathematical basis.
Here is my decision: I will try to find some tasks at my work that include mathematics and see how I can change my situation there by the end of the year. If I don't succeed, I will have to think of something else. Let the Web be my witness. I will report the results to you soon.
I stumbled upon the following sentence in the MathWorld article on the Fibonacci numbers: "No odd Fibonacci number is divisible by 17." I started wondering if there are other numbers like that. Of course there are — no odd Fibonacci number is divisible by 2. But then, an odd number need not be a Fibonacci number in order not to be divisible by 2.
So, let's forget about 2 and think about odd numbers. How do we know that the infinite Fibonacci sequence never produces an odd number that is divisible by 17? Is 17 the only such odd number? Is 17 the smallest such odd number? If there are many such odd numbers, how do we calculate the corresponding sequence?
We'll start with a general question: How can we approach puzzles about the divisibility of Fibonacci numbers? Suppose K is an integer. Consider the sequence aK(n) = Fn(mod K), of Fibonacci numbers modulo K. The cool thing about this sequence is that it is periodic. If it is not immediately obvious to you, think of what happens when a pair of consecutive numbers in the sequence aK(n) gets repeated. As a bonus for thinking you will get an upper bound estimate for this period.
Let us denote the period of aK(n) by PK. By the way, this period is called a Pisano period. From the periodicity and the fact that aK(0) = 0, we see right away that there are infinitely many Fibonacci numbers divisible by K. Are there odd numbers among them? If we trust MathWorld, then all of the infinitely many Fibonacci numbers divisible by 17 will be even.
How do we examine the divisibility by K for odd Fibonacci numbers? Let us look at the Fibonacci sequence modulo 2. As we just proved, this sequence is periodic. Indeed, every third Fibonacci number is even. And the evenness of a Fibonacci number is equivalent to this number having an index divisible by 3.
Now that we know the indices of even Fibonacci numbers we can come back to the sequence aK(n). In order to prove that no odd Fibonacci number is divisible by K, it is enough to check that all the zeroes in the sequence aK(n) have indices divisible by 3. We already have one zero in this sequence at index 0, which is by divisible by 3. Because the sequence aK(n) is periodic, it will start repeating itself at aK(PK) . Hence, we need to check that PK is divisible by 3 and all the zeroes up to aK(PK) have indices divisible by 3. When K = 17 it is not hard to do the calculations manually. If you'd like, try this exercise. To encourage (or perhaps to discourage) you, here's an estimate of the scope of the work for this exercise: the Pisano period for K = 17 is 36.
After I checked that no odd Fibonacci number is ever divisible by 17, I wanted to find the standard solution for this statement and followed the trail in MathWorld. MathWorld sent me on a library trip where I found the proof of the statement in the book Mathematical Gems III by Ross Honsberger. There was a proof there alright, but it was tailored to 17 and didn't help me with my questions about other such odd numbers.
The method we developed for 17 can be used to check any other number. I trusted this task to my computer. To speed up my program, I used the fact that the Pisano period for K is never more than 6K. Here is the sequence calculated by my trustworthy computer, which I programmed with, I hope, equal trustworthiness:
The sequence shows that 9 is the smallest odd number that no odd Fibonacci is ever divisible by, and 17 is the smallest odd prime with this same property. Here is a trick question for you: Why is this property of 17 more famous than the same property of 9?
Let us look at the sequence again. Is this sequence infinite? Obviously, it should include all multiples of 9 − hence, it is infinite. What about prime numbers in this sequence? Is there an infinite number of primes such that no odd Fibonacci number is divisible by them? While I do not know the answer, it's worth investigating this question a little bit further.
From now on, let K be an odd prime. Let us look at the zeroes of the sequence aK(n) more closely. Suppose a zero first appears at the m-th place of aK(n). Then aK(m+1) = aK(m+2) = a. In this case the sequence starting from the m-th place is proportional modulo K to the sequence aK(n) starting from the 0-th index. Namely, aK(n+m) = a*aK(n) (mod K). As a is mutually prime with K, then aK(n+m) = 0 iff aK(n) = 0. From here, for any index g that is a multiple of m, aK(g) = 0. Furthermore, there are no other zeroes in the sequence aK(n). Hence, the appearances of 0 in the sequence aK(n) are periodic with period m.
By the way, m is called a fundamental period; and we just proved that the Pisano period is a multiple of the fundamental period for prime K. Hence, the fact that no odd Fibonacci number is divisible by K is equivalent to the fact that the fundamental period is not divisible by 3. It is like saying that if the smallest positive Fibonacci number divisible by an odd prime K is even, then no odd Fibonacci number is divisible by K.
If the remainder of the fundamental period modulo 3 were random, we would expect that about every third prime number would not divide any odd Fibonacci numbers. In reality there are 561 such primes among the first 1,500 primes (including 2). This is somewhat more than one third. This gives me hope that there is a non-random reason for such primes to exist. Consequently, it may be possible to prove that the sequence of prime numbers that do not divide odd Fibonacci numbers is infinite.
Can you prove that?
Why didn't I think of this before?
I want to share some ideas about mathematics and about my life as a mathematician. In this blog, you'll read about such things as the properties of numbers and sequences and how mathematicians approach practical things.
I started my life as a genius girl mathematician, winning silver and gold medals at the International Math Olympiad (IMO) as a teenager. My PhD is from Moscow State University. When I got married, I wanted to have a family and mathematics at the same time, but being a woman, this affected my mathematics career. Now my kids are growing up and mathematics is becoming more and more important in my life. This is why I decided to start this blog.
Last revised October 2013