
This blog has a modern version at http://blog.tanyakhovanova.com/, where you can leave comments. This page contains the copies of 111 blog entries for 2009. The latest essays are at http://www.tanyakhovanova.com/MathBlog.html
If you enjoy this page you can support it by shopping at amazon through this link. Thank you.
Lottery is a tax on people bad at math.
In this article I calculate how bad the lottery is as an investment, using Mega Millions as an example. To play the game, a player pays $1.00 and picks five numbers from 1 to 56 (white balls) and one additional number from 1 to 46 (the Mega Ball number, a yellow ball).
During the drawing, five white balls out of 56 are picked randomly, and, likewise, one yellow ball out of 46 is also picked independently at random. The winnings depend on how many numbers out of the ones that a player picks coincide with the numbers on the balls that have been drawn.
So what is your expected gain if you buy a ticket? We know that only half of the money goes to payouts. Can you conclude that your return is 50%?
The answer is no. The mathematical expectation of every game is different. It depends on the jackpot and the number of players. The more players, the bigger is the probability that the jackpot will be split.
Every Mega Millions playslip has odds printed on the back side. The odds of hitting the jackpot are 1 in 175,711,536. This number is easy to calculate: it is (56 choose 5) times 46.
How much is 175,711,536? Let's try a comparison. The government estimates that in the US we have 1.3 deaths per 100 million vehicle miles. If you drive one mile to buy a ticket and one mile back, your probability to die is 2.6/100,000,000. The probability of dying in a car accident while you drive one mile to buy a lottery ticket is five times higher than the probability of winning the jackpot.
Suppose you buy 100 tickets twice a week. That is, you spend $10,000 a year. You will need to live for 1,000 years in order to make your chances of winning the jackpot be one out of 10. For all practical purposes, the chance of winning the jackpot are zero.
As the probability of winning the jackpot is zero, we do not need to include it in our estimate of the expected return. If you count all other payouts then you are likely to get back 18 cents for every dollar you invest. You are guaranteed to lose 82% of your money. If you spend $1000 a year on lottery tickets, on average you will lose $820 every year.
If you do not buy a lot of tickets your probability of a big win is close to zero. For example, the probability of winning $250,000 (that is guessing all white balls, and not guessing a yellow ball) by buying one ticket is about 1 in 4 million. The probability of winning $10,000 — the next largest win — is close to 1 in 700,000. If we say that you have no chance at these winnings anyway, then your expected return is even less: it is 10 cents per every dollar you invest.
You might ask what happens if we pool our money together. When a lot of tickets are bought then the probability of winning the jackpot stops being zero. I will write about this topic later. For now this is what I would like you to remember. From every dollar ticket:
I am not at all trying to persuade you not to buy tickets. Lottery tickets have some entertainment value: they allow you to briefly dream about what you would do with those millions of dollars. But I am trying to persuade you not to buy lottery as an investment and not to put more hope into it than it deserves. If you treat lottery tickets as tickets to a movie that is played in your head, you will never buy more than one ticket at a time.
That is it. I advise you not to buy more than one ticket at a time. One ticket will allow you to dream about the expression on your sister's face when she sees your new $5,000,000 mansion, but will not destroy your finances.
Should you allocate time for checking your answers during important tests? I will use AMC 10/12 as an example, but you can adjust the calculations for any other test.
AMC 10/12 is a math competition that asks 25 multiple-choice questions that you need to solve in 75 minutes. You get 6 points for a correct answer, 1.5 points for an unanswered question and 0 points for a wrong answer.
Whether or not to take time to check your answers depends on you and the situation. If you finished your test and have some time left over, then surely you should use the extra time for checking your answers. If you only have three minutes left and your next problems are too complex to be dealt with in that time, then it is logical to use these moments to check back.
Sometimes, though, it isn't worth it to check your answers. If you haven't finished the test, but are a super-accurate person and never make mistakes, then it is better to continue working on the next problem than to waste time checking your correct answers. Also, if you rarely catch your own mistakes anyway, it doesn't make sense to check.
But things are not usually so clear. By the end of the test, most people need to make a decision: continue working through the problems or use the final moments to check the answers? How can you best decide if you should allocate time for checking and, if so, how much time?
The problems in AMC tests increase in difficulty. I suggest that each time you take the test or practice for AMC, take note of two things. How long did it take you to solve the test's last problem and what is the level of your accuracy for it. Suppose you know that at the end of the AMC test you can solve a problem in about 10 minutes and it is correct about 90% of the time. That means that investing the last ten minutes in solving the next problem will give you on average 5.4 points. If you remember that a blank answer gives you 1.5 points, you should realize that solving the last problem increases your score by 3.9 points. If you are very accurate, your score can increase more, but not more than 4.5 points.
Try conducting the following experiment. Take an AMC test from a past year. Do it for 65 minutes — the time of the test minus the time you need for that last problem. Then spend the last 10 minutes checking and correcting your answers. Now let us calculate how profitable that would be. Compare the scores you would have gotten without your corrections and with your corrections. If checking increases your score by more than 3.9 points, it is more profitable to check than to solve the next problem. If you do not make errors when you're trying to make corrections, the rule of thumb is that correcting one mistake is better than solving one problem. Indeed, your score increases by 6 points if you correct a mistake, and by not more than 4.5 points if you solve the next problem.
On all tests that punish wrong answers, correcting an error produces more points than solving a new question.
If you find that checking is profitable, but you can't check all the problems in ten minutes, you should consider allocating more time. Keep in mind, though, that you should adjust the sample calculation above for the last two problems. Remember, the next to the last problem is generally easier than the last problem. So if it takes you ten minutes to solve the last problem in the test, it most probably will take you less than twenty minutes to solve the last two. Also, since the difficulty increases throughout the test, the accuracy of the second to last problem might be better than the accuracy of the last problem. In addition, the first ten minutes that you check may be more productive than the next ten minutes of checking. So if you wonder if you should forgo the last two problems in order to check your earlier work, you have to redo the experiment anew, measuring both how long it takes you to solve those two problems and the benefits of checking.
This discussion can potentially help you to increase your score. However, there are other strategic considerations to weigh when deciding whether or not to check your work. For example, if the number of mistakes in your tests varies and sometimes you are 100% accurate and you are one problem away from your goal to get to AIME, it is more profitable to go for the last problem and hope for the best. I will discuss the strategic considerations for AMC some other time.
This essay is written especially for high school and undergrad math lovers who enjoy problem solving and who plan to major in mathematics. One of the authors, Tanya, often received this advice when she was an undergraduate in Russia: "Problem solving is child's play. You'll have to change your attitude if you plan to succeed in research."
Perhaps that's why some famous problem solvers, even those who won gold medals at IMO, became not-so-famous mathematicians. To help you avoid that fate, we'll discuss the ways in which research is unlike problem solving.
Yes and no. There are many mathematicians who continue problem solving as their form of research. Remember Paul Erdos who used to suggest a lot of problems and even offered money rewards for solutions. Many mathematicians solve problems posed by other people. You might consider Andrew Wiles as the ultimate math problem solver: he proved Fermat's last theorem, which had been open for 400 years. Though he could not have done it without the many theories that had already been generated in the search to find the elusive proof.
You can become a mathematician and continue to look around you for problems to solve. Even though this is still problem solving, the problems will be very different from competition problems, and you will still need to adjust to this type of research.
So, what is the difference between problems that mathematicians solve during competition and the problems they tackle for their research?
Expected answer. In competition problem solving you know there is a solution. Often you know the answer, but you just need to prove it. In research there is no guarantee. You do not know which way it will go. For this reason finding counter-examples and proving that some ideas are wrong is a positive contribution, for it can eliminate some possibilities. So one adjustment is that you might start valuing negative answers.
Difficulty level. Competition problems are designed to be solved in one hour, so you are expected to generate an idea in just minutes. In research the problem might drag on for years, because it is far more difficult. If you get used to the instant gratification of competition problem solving, you might find the lengthy work of research frustrating. It's very important to adjust your expectations so that you won't drop a problem prematurely. You need to measure progress in small intermediate steps and learn to appreciate this different rhythm.
Motivation. Although you miss the euphoria of finding quick solutions, you get a different kind of reward with research. Because no one knows the answer in advance, when you solve the problem, you are the first to do so. You have opened up a new truth.
Time limits. In competitions you have a time limit for every problem. In research you set your time limits yourself. That allows you to put a problem aside and come back later if necessary. In a sense you can think about several problems at the same time.
Your passion. You can choose your problems yourself. Research is much more rewarding if you follow your heart. In competitions you have to spend time on problems you might not like. Here you have an option to choose and pick only the problems that appeal to you. Thus, you become more motivated and as a result more successful.
After solving problems posed by other people, the next step is to pose math problems yourself. As we mentioned before, in research you do not always have a strictly-defined problem. It is a significant adjustment to move from solving already-defined problems to posing the problems yourself.
Generalizations. Often you can generalize from an existing problem to more general cases. For example, if you see a problem for n=3, you can wonder what happens for any n, or for any prime n.
Being on the lookout. Sometimes a situation puzzles you, but you can't formulate a specific problem around that situation. For example, why do most of the terms in the sequence end in 9? Is there a reason for that? Or, you might find that a formula from your integrable systems seminar is similar to a formula from your representation theory class. This might lead you to the essential research question: "What is going on?" You always need to be on the lookout for the right questions.
Value. When you create your own research problems it is crucial to always ask yourself: Is the problem I am creating important? What is the value of this problem? There is no a good reason to create random generalizations of random problems. If the problem you found interests you very much, that is the first sign that it might interest other people; nonetheless, you should still ask yourself how this problem will help advance mathematics.
There are other things to do than solve problems. There are many mathematicians who work differently, who don't solve problems or don't only solve problems. Here are some of the many options mathematicians have:
Building structures. You may not be interested in calculating the answer to a question, but rather in building a new structure or a new theory.
Advancing the language. When you invent new definitions and new notations, you will help to simplify a math language so that the new language will allow you to prove your results and other peoples' results faster and clearer.
Unification. Sometimes you notice two results in two different areas of mathematics with some kind of similarity. Explaining why these results are the same might create a new understanding of things. It is great to unify two different areas of mathematics.
Explaining. Very often proofs are not enough. Why is something true? What's the reason and what's the explanation? It is good to ask yourself a "why" question from time to time, such as, "Why is this proof working?" When you find an answer, it might become easier to understand what to do next and how to generalize your proof.
Directions. Many mathematicians are valued not for the problems they solve or suggest, but for ideas and directions they propose. Finding a new direction for research can generate unexpected opportunities and create tons of math problems on the way. It can be valuable to come up with good conjectures, even if you have no hope of solving them yourself. Two example of this are the Weil conjectures (eventually proved by Deligne) and the Langlands program, which is still incomplete but which has generated a huge amount of important research.
Vision. What is the most general thing that can be proved by this technique? What kinds of improvements and refinements are there? It is good to step back from the problem you solved and meta-think about it.
As you can see, problem solving is just the beginning of all that mathematics can offer you. Mathematicians find these other options very rewarding, so it's worth your while to try these varied aspects of mathematical work to see if you have a taste for other things. If you don't venture beyond problem solving you might miss the full beauty of mathematics.
I could no longer resist: I added a section of physics jokes to my math jokes collection:
* * *
A hydrogen atom says to the bartender, "Hey buddy, have you seen an electron around here? I seem to have lost mine."
"Are you sure you lost it?" the bartender asks.
And the hydrogen atom answers, "I'm positive!"
* * *
Heisenberg gets stopped on the motorway by the police.
Cop: "Do you know how fast you were going sir?"
Heisenberg: "No, but I know exactly where I am."
* * *
A photon checks into a hotel. The bellhop asks him, "Can I help you with your luggage?"
To which the photon replies, "I don't have any. I'm traveling light."
My recent entry, where I asked you to choose the odd one out among these images

was extremely popular. It was republished all around the world and brought my blog as much traffic in one day as I used to get in a month. Not only did I read the many comments I received, I also followed up on other peoples' blogs who reprinted my puzzle — at least those that were in either Russian or English. I also got private emails and had many conversations in person about it. The diversity of answers surprised me, so I would like to share them with you.
As I've said before, I do not think there is a correct answer to this type of question, but I was disappointed by some of the answers. For example, those who simply said, "The green one is the odd one out," made me feel that either they hadn't read the question or hadn't thought about it very much. It's a shame that these people spent more time sharing their opinion with the world than thinking about the problem in the first place.
I wouldn't mind someone arguing that the green one is the odd one out, but in this case an explanation is in order. Many people did offer explanations. Some told me that we perceive the color difference stronger than all other parameters I used, and the green figure pops out of the picture more than anything else. In fact, I personally perceive color difference the strongest among all the parameters, but since there are people who are color blind, I would disregard my feelings for color as being subjective.
You can create a whole research project out of this puzzle. For example, you can run an experiment: Ask the question, but flash the images above very fast, so there is no time for analysis — only time to guess. This allows us to check which figure is the first one that people perceive as different. Or you can vary the width of the frame and see how the perception changes.
Color was not the only parameter among those I chose — shape, color, size and the existence of a frame — that people thought was more prominent. My readers weighed these parameters unequally, so each argued the primary importance of the parameter they most emphasized. For example, one of my friends argued that:
The second figure should be the odd one out as, first, it is the only one without a frame, and, second, it is the only one comprised of one color rather than two. So it differs by two features, as others differ only by one feature.
A figure having one color is the consequence of not having a frame, so this particular friend of mine inflated the importance of not having a frame.
However, I can interpret any feature as two features. For example, I can say that the circle is the odd one out because not only is it a different figure, but it also doesn't have any angles. Similarly, the last one is the smallest one and the border width is in a different proportion to its diameter.
On a lighter side, there were many funny answers to the puzzle:
For the which-is-the-odd-one-out questions, the designer of the question is usually expecting a particular answer. So here's the answer I expected:
There is only one green figure. Wait a minute, there is only one circle. Hmm, there is only one without a frame and there's only one small figure. I see! The first one is the only figure that is not the odd one, that doesn't have a special property, so the first must be the odd one out. This is cool!
And the majority of the answers were exactly as I expected.
Since this is a philosophical problem, some of the responses took it to a different level. One interesting answer went like this:
All right, the last four figures have special features; the first figure is special because it is normal. Hence, every figure is special and there are no odd ones here.
I like this answer as the author of it equated regular features with a meta-feature, and it is a valid choice. This answer prompted me to write another blog entry with a picture where I purposefully tried to not have an odd one out:

Though I wrote that the purpose of this second set of images is to show an example where there is no odd one out, my commentators still argued about which one was the odd one out here.
Finally, I would like to quote Will's comment to my first set of images:
The prevailing opinion is that the first is least unique and is therefore the oddest. But it is the mean and the others are one deviation from it. Can the mean be the statistical anomaly?
And Cedric replied to Will:
Yes, I think the mean can be a statistical anomaly. The average person has roughly one testicle and one ovary. But a person with these characteristics would certainly be an anomaly.
I started my blog about two year ago. I have written about 200 entries. According to my traffic reports, these have been the top ten most popular entries:
My most popular category was Math Humor.
Israel Gelfand's memorial is being held at Rutgers on December 6, 2009. I was invited as Gelfand's student.
My relationship with Gelfand was complicated: sometimes it was very painful and sometimes it was very rewarding. I was planning to attend the memorial to help me forget the pain and to acknowledge the good parts.
I believe that my relationship with Gelfand was utterly unique. You see, I was married three times, and all three times to students of Gelfand.
Now that I know that I can't make it to the memorial, I can't stop wondering how many single male students of Gelfand will be there.
I've translated two problems from the 2009 Moscow Math Olympiad. In both of them our characters are genetically engineered octopuses. The ones with an even number of arms always tell the truth; the ones with an odd number of arms always lie. In the first problem (for sixth graders) four octopuses had a chat:
- "I have 8 arms," the green octopus bragged to the blue one. "You have only 6!"
- "It is I who has 8 arms," countered the blue octopus. "You have only 7!"
- "The blue one really has 8 arms," the red octopus said, confirming the blue one's claim. He went on to boast, "I have 9 arms!"
- "None of you have 8 arms," interjected the striped octopus. "Only I have 8 arms!"
Who has exactly 8 arms?
Not only do octopuses lie or tell the truth according to the parity of the number of their arms, it turns out that the underwater world is so discriminatory that only octopuses with six, seven or eight arms are allowed to serve Neptune. In the next problem (for seventh graders), four octopuses who worked as guards at Neptune's palace were conversing:
- The blue one said, "All together we have 28 arms."
- The green one said, "All together we have 27 arms."
- The yellow one said, "All together we have 26 arms."
- The red one said, "All together we have 25 arms."
How many arms does each of them have?
My students enjoyed the octopuses, so I decided to invent some octopus problems of my own. In the first problem, the guards from the night shift at Neptune's palace were bored, and they started to argue:
- The magenta one said, "All together we have 31 arms."
- The cyan one said, "No, we do not."
- The brown one said, "The beige one has six arms."
- The beige one said, "You, brown, are lying."
Who is lying and who is telling the truth?
In the next problem the last shift of guards at the palace has nothing better to do than count their arms:
- The pink one said, "Gray and I have 15 arms together."
- The gray one said, "Lavender and I have 14 arms together."
- The lavender one said, "Turquoise and I have 14 arms together."
- The turquoise one said, "Pink and I have 15 arms together."
What number of arms does each one have?
An ancient Russian joke:
Patient: Doctor, is there a medicine I can use to prevent my girlfriends from become pregnant?
Doctor: Kefir.
Patient: Should I drink it before or after sex?
Doctor: Instead of.
I have a more pleasurable suggestion than drinking kefir: date postmenopausal women. There are many other reasons why men enjoy dating older women, but since my blog is about mathematics, I would like to dig into some relevant numbers.
We know that boys are born more often than girls, and men die earlier than women. Somewhere around age 30 the proportion in population switches from more boys to more girls. And it gets more skewed with age. So there's a deficit of older men. In addition, a big part of the population is married, making the disproportions in singles group more pronounced. So I decided to look at the numbers to see how misshaped the dating scene is.
This 2008 data comes from the U.S. government census website's table "Marital Status of the Population by Sex and Age: 2008. (Numbers in thousands. Civilian non-institutionalized population.)" To calculate the number of singles, I summed up the widowed, divorced and never married columns.
| Age Group | Single Male | Single Female | Ratio M/F |
|---|---|---|---|
| Total | 44,707 | 51,293 | 0.87 |
| 15 to 17 years | 6,729 | 6,513 | 1.03 |
| 18 to 24 years | 13,074 | 11,848 | 1.10 |
| 25 to 29 years | 6,639 | 5,224 | 1.27 |
| 30 to 34 years | 3,901 | 3,343 | 1.17 |
| 35 to 39 years | 3,354 | 2,965 | 1.13 |
| 40 to 44 years | 3,410 | 3,270 | 1.04 |
| 45 to 49 years | 3,476 | 3,591 | 0.97 |
| 50 to 54 years | 2,979 | 3,385 | 0.88 |
| 55 to 59 years | 2,309 | 3,123 | 0.74 |
| 60 to 64 years | 1,552 | 2,746 | 0.57 |
| 65 to 69 years | 1,082 | 2,423 | 0.47 |
| 70 to 74 years | 787 | 2,162 | 0.36 |
| 75 to 79 years | 790 | 2,391 | 0.33 |
| 80 to 84 years | 685 | 2,430 | 0.28 |
| 85 years and over | 669 | 2,391 | 0.28 |
These data alone cannot explain the dating situation. For example, I have no way of knowing what proportion of each gender isn't interested in dating the opposite sex, or even in dating altogether. But the trend is quite clear: the proportion of men in younger categories is much higher. That implies that there is less competition for older women. So those young men who are open to dating much older women might have more options and those options might be more interesting.
I just turned 50 and plan to return to dating again. Looking at the data I see that there are 11 million single men older than me and 34 million who are younger than me. If I were to pick a single man randomly, I am three times more likely to end up with a younger man.
Supposedly we live in a free society, where people can do what they want as long as they do not harm anyone else. Still our society often disapproves of women dating much younger men. Consider this definition from Wikipedia:
"Cougar — a woman over 40 who sexually pursues a much younger men."
This derogatory term portrays such women as predatory. Not only is there nothing wrong with women dating younger men, but it makes no sense for older women to ignore the imbalance of the dating scene and be closed to relationships with much younger men. After all, the demographics are also affected by the fact that women live longer, probably because of their healthy life style, non-risky behavior and positive attitude to life.
Can someone explain to me again why sane, healthy, non-risky women with positive attitudes to life are called "cougars"?
The first episode of Numb3rs: Season Six reminded me of the hangman's paradox. Here is a one-day version of the hangman's paradox:
Suppose you are in a prison and the guard says to you, "You will be hanged tomorrow at noon and it will be a surprise." You presume that you can't be surprised since they already told you, so there is a contradiction in what they've said. Therefore, you conclude that they can't hang you and you relax. Next day at noon the guard comes for you, to take you to be hanged, and you are utterly surprised. Oops.
What I do not like about this paradox is that it assumes that you do not know about the paradox. I, on the other hand, imagine that you, my reader, are logical and intelligent. So the moment the guard tells you that you will be hanged tomorrow at noon and it will be a surprise, you realize that the situation depends on what you decide to believe in now. If you decide that you won't be hanged tomorrow, then you will have a relatively relaxing day today and you will be caught by surprise tomorrow and die. If you decide that you will die tomorrow, then you will have a nerve-wracking day today, but the guard may release you, to save his honor, since you won't be surprised.
The original hangman's paradox in which the guard tells you that you will be hanged on a weekday the following week and that you will be caught by surprise, also assumes that you are not aware of the paradox. If you are aware of the paradox, you know that usually guards in this paradox come for you on Wednesday, so you can prepare yourself. Actually, to guarantee your survival, if not your feeling of moral superiority, you can daily persuade yourself to belief that you will be hanged at noon the next day. This way, you will never be caught by surprise. If you are a person who can control your own beliefs, you may be able to save your life.
The book An Introduction to Diophantine Equations by Titu Andreescu and Dorin Andrica is targeted at people preparing for USAMO and IMO. It contains a lot of problems on Diophantine equations from math Olympiads used in various math Olympiads all over the world.
The first chapter discusses several methods for solving Diophantine equations: decomposition, using inequalities, using parameters, modular arithmetic, induction, infinite descent, and other miscellaneous ideas. Each sub-chapter starts with a short description of the method, accompanied by several solutions to sample problems. At the end of each sub-chapter there are a plethora of exercise problems.
The second and the third chapters are more theoretical. The former discusses some classical equations and the latter looks at Pell's equation. These two chapters also contain problems, but the bulk of the chapters is devoted to basic theory that is essential to an understanding of Diophantine equations.
For those who are training for the Olympiads, this is an important book to own, not only because there are few other books on the subject, but because it provides so many useful problems.
I've long complained that most training books for math competitions leave out any discussion of how we choose a method by just looking at a problem. Andreescu and Andrica didn't fill that gap with this book.
Perhaps in their next book they will point out clues that indicate that a particular problem might be solved by the parametric method. And explain which types of problems are best solved with induction. Let them challenge students to find those clues in a problem that help us to judge which method might be most promising, instead of randomly trying one method after another. Let me give you a sample problem from the book, which originated at the Balkan Mathematical Olympiad:
Prove that the equation x5 – y2 = 4 has no solutions in integers.
The solution is to take the equation modulo 11, and see that it is impossible.
Is there a reason to start with the modular arithmetic method and not with other methods? If we use modular arithmetic, do we recognize why it's best to start with 11? I'm convinced that this problem has sufficient clues to suggest starting with checking this equation modulo 11.
I wonder if you, my readers, agree with me. If so, can you explain which hints in the problem lead to taking the equation modulo 11? I believe it should be a part of competition training to learn to identify clues that suggest that one direction might be preferable to the others.
I love Harvard-MIT Math Tournaments. I like the mini-events, especially when I learn a new game. I also like the guts round, where I enjoy the adrenaline rush of watching the progress in real time. I also like the fact that I know many of the kids from different teams: my current students, my former students, the members of my club, my Sergei's friends.
The problems for the competitions are designed by undergraduate students at MIT and Harvard. Kudos to them. Still, I was somewhat disappointed with the November 2009 problems. Most problems are variations of standard problems with different parameters. It is not easy to design a problem, but I was hoping for something fresh.
My favorite problem from the HMNT 2009 tournament was in the theme round:
There are five guys named Alan, Bob, Casey, Dan, and Eric. Each one either always tells the truth or always lies. You overhear the following discussion between them:Who are the liars?
- Alan: "All of us are truth-tellers."
- Bob: "No, only Alan and I are truth-tellers."
- Casey: "You are both liars."
- Dan: "If Casey is a truth-teller, then Eric is too."
- Eric: "An odd number of us are liars."
My second favorite problem was in the guts round:
Six men and their wives are sitting at a round table with 12 seats. These men and women are very jealous — no man will allow his wife to sit next to any man except for himself, and no woman will allow her husband to sit next to any woman except for herself. In how many distinct ways can these 12 people be seated such that these conditions are satisfied? (Rotations of a valid seating are considered distinct.)
This was the funniest problem:
You are trapped in ancient Japan, and a giant enemy crab is approaching! You must defeat it by cutting off its two claws and six legs and attacking its weak point for massive damage. You cannot cut off any of its claws until you cut off at least three of its legs, and you cannot attack its weak point until you have cut off all of its claws and legs. In how many ways can you defeat the giant enemy crab? (Note that the legs are distinguishable, as are the claws.)
It is difficult to arrange so many problems for four rounds without mistakes. The error in the following problem is not a typo and it bothers me that no one caught it:
Pick a random digit in the decimal expansion of 1/99999. What is the probability that it is 0?
Hey, there is no uniform distribution on an infinite set of integers: picking a random digit is not defined.
Last month I gave my students a problem from Raymond Smullyan's book The Riddle of Scheherazade:
A certain sheik named Hassan has eight horses. Four of them are white, three are black, and one is brown. How many of them can each say that it is the same color as another one of Hassan's horses?
Half of my students failed to notice the trick and gave the wrong answer. Recently I gave them the continuation of the problem from the same book:
A certain sheik named Hassan has eight horses. Four of them are white, three are black, and one is brown. Assuming now that Hassan's horses can talk, how many of them can each say that it is the same color as another one of Hassan's horses?
This time the majority of my students didn't notice the trick. This motivated me to continue playing jokes with them. Unfortunately though, Raymond Smullyan had only two problems about Hassan's horses, so I have to invent the next one myself. Here is what I plan to give my students next time:
A certain sheik named Hassan has eight horses. Four of them are white, three are black, and one is brown. Assuming now that Hassan's horses can talk and always tell the truth, how many of them will say that it is the same color as another one of Hassan's horses?
Feel free to continue the series.
My recent blog puzzle where my readers had to choose the odd one out became extremely popular and was republished in many blogs around the world. Some commentators decided that my posting was a joke and an example where the odd one out didn't exist. I have to disappoint them: as a protest against find-the-odd-one-out questions and to illustrate that sometimes there is no good choice for the odd one out I would have chosen a different picture:

Can you find the odd one out?
Inspired by Michael Huber, who in his new book Mythematics combines math problems with Greek myths, I invented my first logic puzzle. Unlike Huber, I never had any ambition to help Hercules, but I always wanted to assist Frodo.
The day was passing towards sunset when the Company finally caught a long-awaited gleam of water, from which sparkled flickers of sunlight. As they quietly drew nearer, they laid their eyes on the next obstacle — a river that they had to transverse. The Company was footsore and tired and the hobbits were starving. But they couldn't rest yet. They needed to collect materials with which to construct their raft before it became too dark. By nightfall they managed to build a tiny raft, and eagerly started their supper.
They couldn't wait until dawn to build more rafts, for they needed to cross the river now. So while they rested, Aragorn smoked his pipe and began to contrive a plan.
Aragorn was in charge and there were eight of them. The four hobbits — Frodo, Sam, Merry and Pippin — were not very useful in battle. However, the four strong fighters — Aragorn, Gimli, Legolas and Boromir, who were sworn to protect the ring-bearer Frodo — were the best in the land.
The small raft they had built would not hold a lot of weight. Aragorn and Boromir were the heaviest. Gimli was short, but together with his armor he weighed as much as either Aragorn or Boromir. Each one of these three heaviest warriors was close to the raft's maximum capacity, so they had to each be alone on the raft while crossing the river. Among the strong fighters, only Legolas was able to cross the river with a hobbit. The raft could also accommodate two hobbits.
Weight was not Aragorn's only consideration: the current was dangerously fast. All the strong men could row, but among the hobbits, only Sam was strong enough to row against such a swift current.
Aragorn also worried about the orcs, who were roaming on both sides of the river. He didn't want to leave any hobbit(s) alone on a riverside, without the safeguard of a strong fighter. Because he was the ring-bearer, Frodo needed extra protection. Aragorn wanted Frodo to be accompanied by at least two strong men. But lately Boromir had become restless when he was around the ring and Aragorn couldn't count on him to look after Frodo. That is, while on the riverside, Frodo's protection had to come from two out of the three remaining strong men: Aragorn, Legolas and Gimli.
Can you help Aragorn design a plan to cross the river?
In a Turing test a human judge on one end of an interface interacts with either a computer or another human through this interface. If the judge can't differentiate a machine from a human, then the computer is said to pass the test. One big goal of folks working in Artificial Intelligence is to build a computer that, when subjected to this test, is indistinguishable from a human.
However, while some people are working hard trying to build programs that can pass as humans, other people are working hard inventing tests that can differentiate between humans and those programs. Such tests are sometimes called Reverse Turing tests. As computer science progresses, the programs that are pretending to be humans as well as reverse tests are becoming increasingly complex.
For example, banks frequently want to prevent malicious computer programs from trying to log into their customers' accounts. As a nice touch the judges are computers in this case. There are different methods designed to confirm that a human is trying to log in. In one of them a picture of a word, called CAPTCHA is presented on a screen, and the program requires that this word be typed in.
I wanted a CAPTCHA with words "Turing Test" in it for this posting. I looked online trying to find a way to do it. I couldn't. There is a ton of software that can produce random CAPTCHAs from a dictionary but nothing could do a particular word. Finally, rather than looking for software, I found a human, a kind gentlemen named Leonid Grinberg who with some GIMP help manually implemented a self-referencing " symbolizing the race between computers and tests.

As text recognition software becomes better and better, these CAPTCHAs become more and more difficult to read by a human. The last time I tried to login, I was only able to type the right word on my fourth try. Very soon computers will be better than humans at parsing CAPTCHAs. Humans are loosing the race on visual methods like this one.
Here's another example. Some malicious software can recognize and capture email addresses on webpages to use for spam. While we don't want them to recognize email addresses, we do want people to be able to do so. Thus we need a way to present email addresses as a reverse Turing test.
The standard safety recommendation is to avoid writing out the full and exact email address. Here's an example: billgates AT gmail DOT com. Actually, I think computers are so smart nowadays that they can learn this trick. Another idea is to show a picture of your email address instead of using characters. Here we return to the image idea, which most computers can nowadays recognize.
Another idea of how to hide an email address is to give simple clues, which point to characters in the email address. For example, if you have "4" in your address, you might say that the character is the sum of two and two. I already invented a version of my email address in which each letter of my username is an answer to a simple question. Unfortunately, I think that the question answering systems like Start, as well as its huge new competitor Wolfram Alpha, will learn to answer these questions very soon. I can construct more sophisticated questions, but that would require my readers to spend more time to figure it out including going back to school for a calculus class.
So, recently, I've come up with a new idea. I made the description of my email simpler, but the paragraph describing my email didn't contain all the necessary information:
I have an email account with Yahoo. My account name consists of seven lower case letters: five letters of my first name concatenated with the first two letters of my last name.
People who want to contact me can easily find my name in the title of my webpage or in my url, but I hoped it would take the evil computers some time to figure out what to look for, where it's located and how to turn it into an address.
The day after I changed my contact web page, I went to my math coaching work at AMSA. During my break, I wanted to unwind by solving a light up puzzle, but it appeared that the new security system at AMSA forbids Internet access to all gaming sites. Thus, being still wound up I decided to do some work and went to my personal page for some materials. I was blocked again. The software politely informed me that access to personal websites was not permitted either. Oops. If a computer can understand that it is a personal website, it probably can figure out the name of the corresponding person. Oops-Oops-Oops. I am loosing the race against computers again. My recent idea to protect my email address from spam lasted one day until my first reality check.

In my days of competing in math, I met guys who could solve any geometry problem by using coordinates: first they would assign variables to represent coordinates of different points, then they would write and solve a set of equations. It seemed so boring. Besides, this approach doesn't provide us with any new insight into geometry.
I find geometric solutions to geometry problems much more interesting than algebraic solutions. The geometric solutions that use geometric transformations are often the shortest and the most beautiful.
I.M. Yaglom wrote a great trilogy called The Geometric Transformations. The first book of this trilogy discusses translations, rotations and reflections. The second one — looks at similarity transformations, and the third one talks about affine and projective transformations. A lot of beautiful problems with their solutions are scattered throughout these books. They include all my favorite problems related to transformations.
I think geometry is the weakest link for the USA math team. So we have to borrow the best geometry books from other countries. This trilogy was translated from Russian and Russians are known for their strong tradition of excellence in teaching geometry.
Below you can find sample problems from Geometric Transformations 1, Geometric Transformations 2 and Geometric Transformations 3 — not necessarily in this order.
Problem 1. Let A be a point outside a circle S. Using only a straightedge, draw the tangents from A to S.
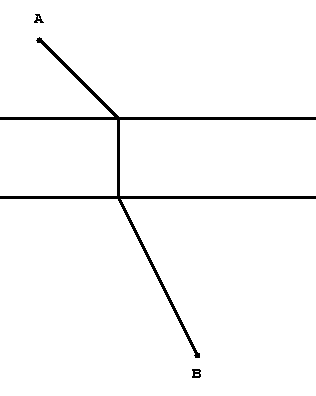
Problem 2. At what point should a bridge be built across a river separating two towns A and B (see figure) in order that the path connecting the towns be as short as possible? The banks of the river are assumed to be parallel straight lines, and the bridge is assumed to be perpendicular to the river.
Problem 3. Suppose you have two lines drawn on a piece of paper. The intersection point A of the two lines is unreachable: it is outside the paper. Using a ruler and a compass, draw a line through a given point M such that, were the paper bigger, point A would belong to the continuation of the line.

I added my favorite webcomics from "Not So Humple Pi" to my collection of funny math pictures.
Suppose you got accepted to the college of your dreams, say MIT. If you are so poor that MIT gives you a full financial package or you are so rich that the cost is not an issue, then you might throw a party. Everyone else, however, needs to wait for the financial package letter from MIT. The dream depends on the willingness and the ability of the parents to pay.
Suppose your father looks at the bill in shock. Then he takes you for a walk and tells you to forget about MIT and go to the state college, as he can't pay the requested amount.
If you know for sure that your father has the money, what is the first question that you should ask him? The first question should be: "Are you still married to my mother?" If you are not completely clueless, you ought to know the answer to this question already. The family status of your parents may be the deciding factor in whether or not you can get your father to pay.
If your parents are divorced, your college expenses might be covered by their divorce agreement. In this case, there would be a legal document designating how your parents need to pay. If your father refuses to pay, your mother can use the divorce agreement to threaten your father with a complaint. The threat might be enough. If it is not, the court will probably force the reluctant father to pay according to the divorce agreement. So if your parents are divorced, it might be a good idea for you to scrutinize their divorce agreement.
Even if your parents' lawyers neglected to include college expenses in the divorce agreement, you might still be able to finance your college education. Your mother, for example, might sue your father for college expenses.
I wonder what happens if the divorce agreement covers your college expenses, but neither parent wants to pay. I'm curious whether or not it is possible for the child to sue the parents based on the agreement he/she is not a party to. If any reader knows the answer, I'd appreciate hearing from you.
If your parents are together, there is no divorce agreement to protect your interests. It seems that legally the situation favors the children of divorced parents. If your parents do not love each other and have stayed in their marriage for your sake, it might be to your financial advantage to persuade them to divorce well before you need to go to college. Do not disregard reminding their lawyers to include college expenses in the agreement.
Israel Gelfand was my scientific adviser from the time I was 15. This is the story of how Gelfand helped me, when at 20 I was an undergrad at Moscow State University. At that time, I was married to Sasha (Alexander) Goncharov, who was also Gelfand's student.
Sasha was more driven by mathematics than I. I had a lot of different interests: I wanted to hang out with friends, go to movies and read books. Sasha only wanted to do mathematics. His only other obsession was with what our colleagues (including me) were doing mathematically. So he was constantly asking me about the math problems I was thinking about.
For example, I was sitting at my side of the desk working, and he asked me to tell him about my problem. A few minutes later, I was forced to interrupt my work to go grocery shopping, because the household chores fell to me. As soon as I returned with bread and milk, Sasha excitedly told me the solution to my problem. It made me feel stupid, as if I should have solved it while I was waiting in the line for bread and milk. That feeling blocked out all the other feelings I should have been noticing, such as frustration and annoyance with Sasha.
Without his interference, I would have happily solved the problem myself. I was about to start my serious research, but I worried that I'd end up as a supplier of new problems for his papers.
You might wonder why I didn't stop sharing my math with Sasha. But at that time, I wasn't very in touch with my feelings and I prided myself on being a logical person. The idea that a husband and wife would discuss their work together seemed logical. Besides, even though I wasn't particularly interested, Sasha was always ready to tell me about his math problems. It seemed important for me to be fair and to reciprocate. So I was stuck in a situation I didn't know how to resolve.
I never confided this issue to any math colleagues. I never mentioned it to Gelfand — mostly because I was too scared of him to initiate any conversation. Besides, Gelfand delegated most of his responsibilities to others, because he was quite famous and busy. For example, all official paperwork related to his adviser role was done by Alexandre Kirillov. With me avoiding Gelfand and Gelfand being busy, we almost never spoke one-on-one.
You can understand my surprise when one day Gelfand approached Sasha and me to have a chat. He told us that we were about to start our own research, and while he permitted me to ask Sasha about what he was doing, he would not allow Sasha to interfere with my research.
Gelfand was a great judge of character. Without anyone telling him, he perceived what was going on in our marriage and gave me an excuse to stop Sasha's prying. It was an appreciated gift.
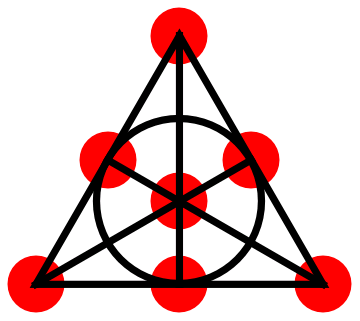
I am strongly opposed to questions of the type "which is the odd one out" during IQ tests. On the other hand, I do not mind them in different settings, especially when they are fun. Inspired by Martin Gardner, I spent a lot of time drawing this picture, and now I have to share it with the world. So, which is the odd one out?

I love the MIT Mystery Hunt. I like the adrenalin rush when solving problems under pressure. Plus, I like the togetherness of doing problems with other people. During the hunt I usually do not have time to look at all the puzzles: some of them are solved by my teammates while I'm sleeping and others are solved before I get to see them.
I've never tried to go back and check out the puzzles I missed nor the puzzles from the previous hunts, probably because without the goal of winning and without my team, I might find them boring. Often the solving process involves tedious Internet browsing to identify the images of different people or objects. I would only be motivated if the puzzle were related to something I am very interested in, such as Ballroom dancing. But I'm not thrilled at the thought of browsing through all the problems in order to find one that is relevant to the Tango.
In short, I need an index to the puzzles. For example, it would be nice to direct the lovers of square dancing to the Do Sa Do puzzle, or fans of Star Trek to the Alien Species puzzle. I hope that nobody blames me for hinting that those aliens are from Star Trek. I'm convinced that Trekkies who only want to solve Star Trek-related puzzles would immediately recognize them anyway. I do believe that I am not revealing too much by saying that the Facebook puzzle will appeal to the aficionados of the television show "24".
It would be extremely useful to humanity to at least mark the MIT Mystery Hunt puzzles that are self-consistent, and do not require activities. For example, some of the puzzles involve interaction with headquarters, so you can't solve them after the hunt. Some of the puzzles might expire, as for example the puzzle with pictures of different announcements in the infinite corridor.
Unfortunately, such an index doesn't exist, and I do not have the time or expertise to create one myself. But I can fill this void at least partially by presenting a guide to math puzzles from the previous four hunts. I can't promise that my guide is complete, as navigating the MIT Mystery Hunt website is very tiresome.
Before going into the math puzzles, I would like to list Sergei's favorite type of puzzle: Duck Konundrums. The first Duck Konundrum puzzle appeared in 2000. It was created by Dan Katz, which is why his initials are in the title. One really needs to follow the instructions for this puzzle. This is very unusual as traditionally hunt puzzles do not have instructions at all. Do not be relieved: the instructions are really very complicated. The next Duck Konundrum puzzle appeared in 2002 and was considered to be even more amusing. People loved it, and this type of puzzle became a tradition in subsequent hunts. Here is my list of Duck Konundrums:
Many Mystery Hunt puzzles appeal to mathematicians. I have to warn you though. Puzzles often are divided into two stages. In the first stage, you need to solve a puzzle, like solving sudoku, a crossword or finding all the wedding dates of the people in the pictures. The second stage requires you to produce a word or a phrase that is the answer to the puzzle. The second stage might be as simple as listing the people in chronological order of their wedding dates and then taking the first letters of their last names. This second stage could also be quite difficult. Depending on your tastes one stage of the puzzle might be much more rewarding than the other. If you love solving sudokus, you might find it more fun to just stop with that solution, instead of continuing on to the second stage.
2006
2007
2008
2009
It would also be nice to have some ratings for puzzles. I am not sure how to persuade the webmasters of the MIT Mystery Hunt page to do the index and the rating. Feel free to send them an encouraging email.

In the book "Mythematics: Solving the Twelve Labors of Hercules" Michael Huber adds details to Hercules' labors so that in order that he can do each task, you need to help Hercules solve two or three math problems. For example, to defeat the Nemean Lion Hercules needs to solve the problem "Zeus Makes a Deal", which is a Greek-myth version of the Monty Hall problem.
The problems in Mythematics are quite advanced. They range in topic from algebra, geometry and probability to differential equations and integral calculus. Plus, as a reward for helping Hercules, Huber gives you variations on Sudoku puzzles.
Solving some nice math problems might not be the only reason for people to buy this book. Here are some other reasons:
I like Huber's approach. Future possibilities for more books are endless. Let's write new math problems based on Harry Potter, Batman, the Bible or, maybe, The Joy of Sex.
Konstantin Knop sent me the following coins puzzle, which was created by Alexander Shapovalov and first appeared at the Regional round of the all-Russian math Olympiad in 2000.
Baron Münchhausen has 8 identical-looking coins weighing 1, 2, …, 8 grams. The Baron knows which coin is which and wants to demonstrate to his guests that he is right. He plans to conduct one weighing on a balance scale, so that the guests will be convinced about the weight of one of the coins. Can the Baron do this?
This being a sequence-lover blog, we want to create a sequence out of this puzzle. The sequence is the following: Let the Baron initially have n identical-looking coins that weigh exactly 1, 2, …, n grams. Then a(n) is the minimum number of weighings on a balance scale that the Baron needs in order to convince his guests about the weight of one of those coins.
The original puzzle can be restated as asking whether a(8) = 1. The sequence is defined starting from index 1 and the first several terms are easy to calculate: 0, 1, 1, 1, 2, 1, 1, 1. Can you continue this sequence?
Let's look at where ones occur in this sequence:
Theorem. If the weight of a coin can be confirmed with one weighing, then one cup of that weighing must contain all the coins with weights from 1 to some i, and the other cup must contain all the coins with weights from some j to n. Furthermore, either the scale must balance, or the cup containing the 1-gram coin must be lighter.
Proof. What does it mean for the Baron to convince his guests about the weight of some coin with one weighing? From the perspective of the guests, a weighing is a number of coins in one cup, a number of coins in the other cup, and a number of coins not on the scale, together with the result the scale shows (one or the other cup heavier, or both the same weight). For the guests to be convinced of the weight of some particular coin, it must therefore be the case that all possible arrangements of coin weights consistent with that data agree on the weight of the coin in question. Our proof strategy, therefore, is to look for ways to alter a given arrangement of coin weights so as to change the weight given to the coin whose weight is being demonstrated, thus arriving at a contradiction.
First, obviously, the coin whose weight k the Baron is trying to confirm has to be alone in its group: either alone on some cup or the only coin not on the scale. After that we can divide the proof of the theorem into several cases.
Case 1. The coin k is on a cup and the scale is balanced. Then we want to show two things: k = n, and the coins on the other cup weigh 1, 2, …, i grams for some i. For the first part, observe that if k < n, then the coin with weight k+1 must not be on the scale (otherwise it would overbalance coin k). Therefore, we can substitute coin k+1 for coin k, and substitute a coin one gram heavier for the heaviest coin that was on the other cup, and produce thereby a different arrangement with the same observable characteristics but a different weight for the coin the Baron claims has weight k.
To prove the second part, suppose the contrary. Then it is possible to substitute a coin 1 gram lighter for one of the coins on the other cup. Now, if coin k-1 is not on the scale, we can also substitute k-1 for k, and again produce a different arrangement with the same observable characteristics but a different weight for the coin labeled k. On the other hand, if k-1 is on the scale but k-2 is not, then we can substitute k-2 for k-1 and then k-1 for k and the weighing is again unconvincing. Finally, if both k-1 and k-2 are on the scale, and yet they balance k, then k=3 and the theorem holds.
Consequently, k = n = 1 + 2 + … + i is a triangular number.
Case 2. The coin k is on the lighter cup of the scale. Then: first, k = 1, because otherwise we could swap k and the 1-gram coin, making the light cup lighter and the heavy cup heavier or unaffected; second, the 2-gram coin is on the heavy cup and is the only coin on the heavy cup, because otherwise we could swap k with the 2-gram coin and not change the weights by enough to affect the imbalance; and finally n = 2 because otherwise we could change the weighing 1 < 2 into 2 < 3.
Thus the theorem holds, and the only example of this case is k = 1, n = 2.
Case 3. The coin k is on the heavier cup of the scale. Then k = n and the lighter cup consists of some collection of the lightest available coins, by the same argument as Case 1 (but even easier, because there is no need to maintain the balance). Furthermore, k must weigh exactly 1 gram more than the lighter cup, because otherwise, k-1 is not on the lighter cup and can be substituted for k, making the weighing unconvincing.
Consequently, k = n = (1 + 2 + … + i) + 1 is one more than a triangluar number.
Case 4. The coin k is not on a cup and the scale is not balanced. Then, since k must be off the scale by itself, all the other coins must be on one cup or the other. Furthermore, all coins heavier than k must be on the heavier cup, because otherwise we could make the lighter cup even lighter by substituting k for one of those coins. Likewise, all coins lighter than k must be on the lighter cup, because otherwise we could make the heavier cup even heavier by substituting k for one of those coins. So the theorem holds; and furthermore, the cups must again differ in weight by exactly 1 gram, because otherwise we could swap k with either k-1 or k+1 without changing the weights enough to affect the result on the scale.
Consequently, the weight of the lighter cup is k(k-1)/2, the weight of the heavier cup is 1 + k(k-1)/2. Thus the total weight of all the coins is n(n+1)/2 = k2+1. In other words, case 4 is possible iff n is the index of a triangular number that is one greater than a square.
Case 5. The coin k is not on a cup and the scale is balanced. This case is hairier than all the others combined, so we will take it slowly (noting first that all the coins besides k must be on some cup).
Lemma 1. The two coins k-1 and k-2 must be on the same cup, if they exist (that is, if k > 2). Likewise k-2 and k-4; k+1 and k+2; and k+2 and k+4.
Proof. Suppose they're not. Then we can rotate k, k-1, and k-2, that is, put k on the cup with k-1, put k-1 on the cup with k-2, and take k-2 off the scale. This makes both cups heavier by one gram, producing a weighing with the same outward characteristics as the one we started with, but a different coin off the scale. The same argument applies to the other three pairs of coins we are interested in, mutatis mutandis.
Lemma 2. The four coins k-1, k-2, k-3 and k-4 must be on the same cup if they exist (that is, if k ≥ 5).
Proof. By Lemma 1, the three coins k-1, k-2, and k-4 must be on the same cup. Suppose coin k-3 is on the other cup. Then we can swap k-1 with k-3 and k with k-4. Each cup becomes heavier by 2 grams without changing the number of coins present, the balance is maintained, and the Baron's guests are not convinced.
Lemma 3. If coin k-4 exists, that is if k ≥ 5, all coins lighter than k must be on the same cup.
Proof. By Lemma 2, the four coins k-1, k-2, k-3 and k-4 must be on the same cup. Suppose some lighter coin is on the other cup. Call the heaviest such coin c. Then, by choice of c, the coin with weight c+1 is on the same cup as the cluster k-1, &hellip, k-4, and is distinct from coin k-2 (because c is on a different cup from k-3). We can therefore swap c with c+1 and swap k with k-2. This increases the weight on both cups by 1 gram without changing how many coins are on each, but moves k onto the scale. The Baron's guests are again unconvinced.
Lemma 4. The theorem is true for k ≥ 5.
Proof. By Lemma 3, all coins lighter than k must be on the same cup. Further, if a coin with weight k+4 exists, then by the symmetric version of Lemma 3, all coins heavier than k must also be on the same cup. They must be on the other cup from the coins lighter than k because otherwise the scale wouldn't balance, and the theorem is true.
If no coin with weight k+4 exists, that is, if n ≤ k+3, how can the theorem be false? All the coins lighter than k must be on one cup, and their total weight is k(k-1)/2. Further, in order to falsify the theorem, at least one of the coins heavier than k must also be on that same cup. So the minimum weight of that cup is now k(k-1)/2 + k+1. But we only have at most two coins for the other cup, whose total weight is at most k+2 + k+3 = 2k + 5. For the scale to even have a chance of balancing, we must have
k(k-1)/2 + k+1 &le 2k + 5 ⇔ k(k-1)/2 ≤ k + 4 ⇔ k(k-1) ≤ 2k + 8 ⇔ k2 - 3k - 8 ≤ 0.
Finding the largest root of that quadratic we see that k < 5.
So for k ≥ 5, the collection of all coins lighter than k is heavy enough that either one needs all the coins heavier than k to balance them, or there are enough coins heavier than k that the theorem is true by symmetric application of Lemma 3.
Completion of Case 5. It remains to check the case for k < 5. If n > k+3, then coin k+4 exists. If so, all the coins heavier than k must be on the same cup. Furthermore, since k is so small, they will together weigh more than half the available weight, so the scale will be unbalanceable. So k < 5 and n ≤ k+3 ≤ 7.
For lack of any better creativity, we will tackle the remaining portion of the problem by complete enumeration of the possible cases, except for the one observation that, to balance the scale with just the coin k off it, the total weight of the remaining coins, that is, n(n+1)/2 - k must be even. This observation cuts our remaining work in half. Now to it.
Case 5. Seven Coins. n = 7. Then 5 > k ≥ n - 3 = 4, so k = 4. Then the weight on each cup must be 12. One of the cups must contain the 7 coin, and no cup can contain the 4 coin, so the only two weighings the Baron could try are 7 + 5 = 1 + 2 + 3 + 6, and 7 + 3 + 2 = 1 + 5 + 6. But the first of those is unconvincing because k+1 = 5 is not on the same cup as k+2 = 6, and the second because it has the same shape as 7 + 3 + 1 = 2 + 4 + 5 (leaving out the 6-gram coin instead of the asserted 4-gram coin).
Case 5. Six Coins. n = 6. Then 5 > k ≥ n - 3 = 3, and n(n+1)/2 = 21 is odd, so k must also be odd. Therefore k=3, and the weight on each cup must be 9. The 6-gram coin has to be on a cup and the 3-gram coin is by presumption out, so the Baron's only chance is the weighing 6 + 2 + 1 = 4 + 5, but that doesn't convince his skeptical guests because it looks too much like the weighing 1 + 3 + 4 = 6 + 2.
Case 5. Five Coins. n = 5. Then 5 > k ≥ n - 3 = 2, and n(n+1)/2 = 15 is odd, so k must also be odd. Therefore k=3, and the weight on each cup must be 6. The only way to do that is the weighing 5 + 1 = 2 + 4, which does not convince the Baron's guests because it looks too much like 1 + 4 = 2 + 3.
Case 5. Four Coins. n = 4. Then the only way to balance a scale using all but one coin is to put two coins on one cup and one on the other. The only two such weighings that balance are 1 + 2 = 3 and 1 + 3 = 4, but they leave different coins off the scale.
The remaining cases, n < 4, are even easier. That concludes the proof of Case 5.
Consequently, by the argument similar to the one in case 4 we can show that the number of coins in case 5 must be the index of a square triangular number.
This concludes the proof of the theorem.
Now we can describe all possible numbers of coins that allow the Baron to confirm a coin in one weighing, or, in other words, the indices of ones in the sequence a(n). The following list corresponds to the five cases above:
If we have four coins, then the same weighing 1+2 < 4 identifies two coins: the coin that weighs three grams and is not in a cup and the coin weighing four grams that is in a cup. The other case like this is for two coins. Comparing them to each other we can identify each of them. It is clear that there are no other cases like this. Indeed, for the same weighing to identify two different coins, it must be the n-gram on the cup, and the n-1 coin off the scale. From here we can see that n can't be big.
As usual we want to give something to think about to our readers. We have given you the list of sequences describing all the numbers for which the Baron can prove the weight of one coin in one weighing. Does there exist a number greater than four that belongs to two of these sequences? In other words, does there exist a total number of coins such that the Baron can have two different one-weighing proofs for two different coins?
To conclude this essay we would like to note that the puzzle we are discussing is related to the puzzle in one of Tanya's previous posts:
You have 6 coins weighing 1, 2, 3, 4, 5 and 6 grams that look the same, except for their labels. The number (1, 2, 3, 4, 5, 6) on the top of each coin should correspond to its weight. How can you determine whether all the numbers are correct, using the balance scale only twice?
The latter puzzle appeared at the last round of Moscow math Olympiad in 1991. The author of this problem was Sergey Tokarev.

I would like to tell you a story from my childhood and how I started on my math path.
When I was in elementary and middle school, I was very good with mathematics. Actually, I was by far the best math student in my class and my math teacher didn't know what to do with me. Our algebra book had 2,000 problems and was intended to cover three years of study. But I worked out those problems, one after another, whenever I had a free minute in my math class. As I result, I got way ahead of everyone else.
One day a new boy named Lenya Kostyukov joined our class. He had extraordinarily long eye-lashes that covered his eyes, and all the girls envied him. He was a nice smart kid, but other than his lashes, I didn't notice him very much. After a year or two, he announced that he was leaving our school, because he had been accepted to a math school for gifted children.
"Why is he going to a math school? I am the math star here. Why aren't I going to a math school?" I knew about math schools, and I knew that I was good at math; I just never made the connection. I never felt that I was supposed to apply. Despite enjoying my reputation, I just passively went with the flow. Lenya figuratively kicked me in the butt. If he can, why can't I?
So I applied to the same school on the last permissible day and was accepted. It turned out that I accidentally went to the room where they were giving the test for a grade higher than mine. I passed it with flying colors. My parents, though, were scared of a long commute and didn't really want me to go so far away. They found a different math school closer to home, and used my extraordinary results to convince that school to accept me, even though their application date had passed.
For many years I continued to be a very passive person. Applying to a math school was the single big step I took for myself, but it was a defining step. I am grateful to Lenya for that. Or more likely to his parents, who were actively looking around trying to find the best place for their gifted son, and as a byproduct found a place for me. Once I was on the path of mathematics, I had the guidance of teachers and supervisors, for better or for worse, which allowed me to continue to be passive.
I have described my defining moment to you, but I don't want to leave you in the dark about Lenya's fate. Here's what happened to him.
As I mentioned, Leonid (Lenya's formal name) and I ended up in different math schools, so I lost track of him. Four years later I went to study math at Moscow State University and stumbled upon a guy with very long eye-lashes. We recognized each other immediately and eventually became friends.
He was doing logic and was very good at it. He was recommended for graduate school. But by that time our MSU administration noticed his lashes too. The lashes were obviously very suspicious; they hinted at the existence of non-Russian blood in his veins. As it was the period of brutal anti-semitism at MSU, they didn't allow him to go to graduate school.
Leonid Kostyukov dropped mathematics and became a famous writer.
Here is a strange puzzle that was inspired by the palindrome problem. Suppose you have a sequence of words in some alphabet with the initial term a and all the other terms b: a, b, b, b, b, etc. Suppose this sequence generates palindromes every time you concatenate the first several terms, not counting the first term itself. So, ab, abb, abbb, and so on — are all palindromes. We call words b "papaya" words, when a exists, such that a and b generate the sequence with this palindrome property. Can you describe papayas?
Theorem. The word b is a papaya word if and only if b is a substring of Reverse(b)Reverse(b).
Proof. After we have added b so many times that the initial part a is much smaller than half of the concatenated string, the middle part of the concatenated string would consist of several words copies of the word b. The middle of the reverse string consists of several concatenations of Reverse(b). So the word b must be a substring of Reverse(b)Reverse(b). On the other hand, suppose b is a substring of Reverse(b)Reverse(b). Then Reverse(b)Reverse(b) is of the form xby, and we can choose a = y.
Theorem. Papaya words are either palindromes or concatenations of two palindromes.
Proof. Suppose our word consists of two palindromes cd. Then the reverse of it is dc and its double is dcdc. The word cd is a substring of dcdc, thus according to the first theorem, cd is a papaya word. Let's do the other direction. Suppose the word b is a substring of Reverse(b)Reverse(b). Then Reverse(b)Reverse(b) is of the form xby. Then b = yx, and Reverse(b) = xy, which equals Reverse(x)Reverse(y). From here, Reverse(x) = x and Reverse(y) = y. If x or y has zero length, then our word is a palindrome. QED.
Hey, do you already know why we call these words papayas?
Just for fun we would like to study the structure of papaya words. Any one-character or two-character word is a papaya word, so the patterns are: a, aa, ab. For three-character words there are four patterns: aaa, aab, aba, abb. For four-character words there are 10 patterns: aaaa, aaab, aaba, abaa, aabb, abab, abba, abbb, abac, abcb. In this manner we get the sequence of the number of n-character papaya patterns: 1, 2, 4, 10, 21, 50 etc, which is sequence A165137 in the OEIS. This sequence depends on the number of letters in your alphabet. But the first n terms of these sequences are the same for all alphabets that have at least n letters.
Let us assume that we are working with an infinite alphabet. The complementary sequence would be the number of patterns for non-papaya words. The total number of patterns is described by sequence A000110 — Bell numbers: the number of word structures of length n using an infinite alphabet. So the beginning of this complementary sequence A165610 is: 0, 0, 1, 5, 31, 153, etc. The list of corresponding patterns is abc, aabc, abbc, abcc, abca, abcd, etc.
Historically, we first invented the corresponding sequence for numbers, not for words. We call a number a papaya number if it is a palindrome or a concatenation of two palindromes. If we use numbers instead of words in the problem, we need to carefully look at what happens if we encounter initial zeroes. Let's take the papaya number 2200100, and see if we can find a number a, such that adding 22010 repeatedly to this sequence starting with a will always generate a palindrome. The number a must be 00100. But this is not a number. We have two choices: to say that we are working with strings of digits, or to allow several numbers to start the sequence before we add b repetitively and before getting to palindromes. In the latter case our sequence can start 0, 0, 100, 22010, 22010, and so on.
As we mentioned before, the number of patterns of papaya numbers will start the same as the number of patterns of papaya words. Later the sequence of patterns of numbers A165136 will be smaller than the corresponding sequence for words. As the sequence of Bell numbers is much more famous than the sequence A164864 of patterns of numbers, we expect the papaya patterns sequence corresponding to the infinite alphabet to be more interesting and important than the sequence of papaya patterns for numbers.
Though papaya numbers might be less important than papaya words with an infinite alphabet, they have an advantage in that we can generate more sequences with them. For example we can calculate the number of positive papaya number with n digits, as in the sequence A165135: 9, 90, 252, 1872, 4464, 29250, etc. And we can also calculate the sequence A165611 of n-digit non-papaya numbers: 0, 0, 648, 7128, 85536 etc.
This geometric problem was given to me by Arkady Berenstein:
There are n points on the plane, but not all of them are on one line. Prove that a line exists that passes through exactly two points of this set.
Arkady gave me a beautiful solution to this problem. First, draw a line through each pair of points. Suppose you calculate all the distances from each point to all the lines that the point doesn't belong to. Pick the smallest distance. The corresponding line will be the one with two points. To finish the solution you need to fill in the details. That process is usually left to the reader.
I suspect that there might also be a solution using linear algebra. Can you find one?
I would like to reformulate this problem without using geometry. Suppose there is a set of n elements. Let's call a family of subsets line-like if any two distinct subsets of this family can have as an intersection not more than one element. Then the geometry problem above has a set-theoretical analogue:
You have a set of n elements and a line-like family of subsets of this set such that any two elements of the set belong to a subset from this family, and that the family doesn't contain the whole set. Is it true that there always exists a subset in this family consisting of two elements?
Usually I give such problems as homework for the reader, but this time I decided to change my habit, so I'm including the picture which contains the solution of this problem by my son Alexey Radul.
Conclusion: geometry is important.
I remember this question from my childhood:
Why is the South Pole colder than the North Pole?
Indeed, the average winter temperature at the North Pole of -34°C is the same as the temperature at the South Pole at the beginning and end of its summer. The South Pole is only warmer than the North Pole 40 days per year. So the South Pole is a much, much colder place. According to Wikipedia there are three major reasons for this:
I remember when I was a child my father gave me a completely different explanation.
The Earth's orbit is not a circle, but rather an ellipse. According to Kepler's second law: "A line joining a planet and the sun sweeps out equal areas during equal intervals of time." This means that the earth has a slower angle motion around the aphelion — in its furthest point — than around the perihelion — in its closest point to the Sun. Consequently, the summer is longer than the winter for the North Pole, whereas the opposite is true for the South Pole.
Something in my father's explanation bothered me. Now I understand what: though the summer is longer at the North Pole, it should get less sunshine as the North Pole is further away from the Sun than the South Pole during its summer. So the effects might cancel each other out. In any case, as the earth's orbit is almost circular, the contribution of the shape of the orbit should be minor, compared to the effects of elevation, the water underneath and continentality.
On the other hand, it is possible that my father wasn't talking about the poles, but rather about the difference in hemispheres. I wonder if someone can calculate if there is a difference in the amount of sunlight the poles get due to the fact that the Earth's orbit is not circular. Is the temperature different for the places that are equidistant from the equator, and have similar elevation and continentality, but which are located in different hemispheres?
I remember a funny article explaining why the northern hemisphere has more land. They said that continents drifted into the northern hemisphere because they wanted a nicer climate.

I bought the book "Heard on The Street: Quantitative Questions from Wall Street Job Interviews" by Timothy Falcon Crack several years ago when I was looking for a job and felt that working in finance was a possibility. Despite having bought it simply to prepare for employment interviews, I actually enjoyed the math problems in the book.
The book has problems in logic, probability, statistics and finance, as well as a very useful chapter of general interview questions. If you're interested in buying this book, I should mention that some questions require calculus and knowledge of financial terms.
I love the author's taste in problems, and here are some sample questions from the book.
Question 2.7: How many degrees (if any) are there in the angle between the hour and minute hands of a clock when the time is a quarter past three?
Question 5.1.14: Welcome to your interview. Sit in this chair. Excuse me while I tie your arms and legs to the chair. Thank you. Now we are going to play "Russian roulette." I have a revolver with six empty chambers. Watch me as I load the weapon with two contiguous rounds (i.e., two bullets side-by-side in the cylindrical barrel). Watch me as I spin the barrel. I am putting the gun against your head. Close your eyes while I pull the trigger. This is your lucky day: you are still alive! Our game differs from regular Russian roulette because I am not going to add any bullets to the barrel before we continue, and I am not going to give you the gun.
My question for you: I am going to shoot at you once more before we talk about your résumé. Do you want me to spin the barrel once more, or should I just shoot?
Question 6.1.16: Tell me something you tried but ended up quitting on.
I can tell you what I would have answered to the last question: I tried smoking, but ended up quitting.
Mathematically we can describe a marriage by a graph. People are vertices and two spouses are connected by an edge.
Mathematical models tend to oversimplify life, so let us assume that a person can only be one of two genders. Therefore, the vertices of a graph are colored in two colors: pink and blue. In this article I explore the graph theory of different types of marriages.
A monogamous couple is represented as a complete K2 graph: two vertices connected by an edge. The graph is bipartite, no matter how you color it. But actually our vertices are already colored from the start. If we are considering traditional marriage, one vertex is pink and the other is blue.
Historically, the second most common type of marriage is polygyny, in which one man has several wives. Less common in history, but a mathematically equivalent type, is polyandry, in which one woman has several husbands. Both these types of marriages emphasize inequality, as husbands and wives have completely different sets of rights.
From a mathematical point of view, polygyny and polyandry are described by star graphs. Star graphs are bipartite graphs and the natural coloring is the one that proves bipartiteness.
The final type of marriage is polygynandry, which refers to a group marriage, where more than one man and more than one woman create a family. Everyone can have sex with everyone else of the other gender. Mathematically this type of marriage corresponds to a complete bipartite graph Kn,m. Actually, in this case I can imagine that a particular pair of people of different genders wouldn't like each other and might not consummate their marriage. So this graph is not necessarily complete.
How can same-sex marriages change the graph theory of marriages? As a graph, a monogamous same-sex marriage is the same bipartite K2 graph as a heterosexual marriage. It will just be less colorful, as both vertices will be of the same color.
But what happens if we add the same-sex idea to polygamous marriages?
Suppose a homosexual man wants to live with several spouses at the same time. What name can we give to a family unit of more than two homosexual men? Homopolygamy? Their marriage graph will be a star graph in which all the vertices are of the same color.
If a man can have several spouses, what about his spouses? Can they form multiple marriages too? If only one person is allowed to engage in several marriages, then we will see inequality within the same gender. If any spouse is allowed to form other marriages, then we will have a situation in which several men are all spouses to each other. So mathematically we will see complete graphs with more than two vertices to represent a marriage. If two people in a group do not like each other and do not want to be married, then the corresponding graph doesn't need to be complete.
By symmetry we can describe a marriage of several women, and mathematically it will be similar to a marriage of several men.
Another interesting aspect is the idea of mixed types of marriages involved in polygamy. Suppose a husband has several wives. Some of them might get bored waiting for his attention, and start spending so much time with each other that they end up developing feelings for each other. Suppose two wives of the same man decide to marry each other. What name would we give to this type of marriage? I am afraid that we do not have enough words to cover all the potential situations.
Suppose we have a heterosexual married couple and the man decides to bring another woman into their house. Thus the transition from a traditional marriage to a polygyny is created. If they got along so well that the first wife decides to marry the second wife, this would require a transition to a new type of marriage. Oh, I see that my essay just went in another direction — how different types of marriages might evolve into each other. For now, I'll leave this for future research.
Talking about different directions. I recently wrote a piece about condoms. Now I have a new generalization for the classic condom puzzle. Suppose we have a mixed-type marriage defined by a graph. Suppose tonight every couple of people corresponding to the edge of this graph wants to have sex with each other. What is the smallest number of condoms they can use? In my condom essay, I didn't define the condom usage for the sex of two women. I will leave it to your imagination and definition.
What follows is the story of a pair of integer sequences, which started life as a Google interview puzzle back in the previous century when VHS video tapes were in use:
Suppose you are buying VHS tapes and want to label them using the stickers that came in the package. You want to number the tapes consecutively starting from 1 and the stickers that come with each package are exactly one of each digit ["0"..."9"]. For your first tape you use only the digit "1", and save all the other digit stickers for later tapes. The next time you will need a digit "1" will be for tape number 10. By this time you will have several unused "1" stickers. What is the next tape number such that after labeling the tape with that number you will not have any "1" stickers remaining?
We can formalize this puzzle in the following way:
Consider a function f which, for a given whole number x, returns the number of times that the digit 1 is needed to write all of the numbers between one and x. For example, f(13) = 6. Notice that f(1) = 1. What is the next largest x such that f(x) = x?
Thus f(x) is the number of "1" stickers needed to label all the tapes up to tape x. When f(x) = x then we have used all of the "1" stickers in labeling the first x tapes.
Let's consider any non-zero digit. In the single and double-digit numbers, there are ten of each digit in the ones column, and ten of each digit in the tens column, so 20 altogether. Early on, the tape number is ahead of the digit count. By the time we get to 20-digit numbers, though, there should be, on average, two of any single non-zero digit per number. Thus, the number of times that any digit is used should eventually catch up with the tape numbers.
Encouraged by assurance of reaching our goal somewhere, we might continue our estimate. In the up-to three-digit numbers there are 300 of each non-zero digit; in the numbers below 10,000 there are 4000; then 50,000, and so on up to 1010, where f(x) and x must (almost) meet. In particular, there are 10,000,000,000 counts for any non-zero digit in the numbers below 10,000,000,000. Hence, were the puzzle asking about any of the digits 2–9, then ten billion could have been an easy answer or, at least a limit on how far we need to search.
Sadly, there is a 1 in the decimal representation of ten billion (and a few zeroes), so we require 1010+1 of the digit "1" to write the numbers [1…1010]. Thus, f(1010) ≠ 1010, so 1010 cannot be the answer to the original puzzle. Thus stymied, Gregory wrote a program to find the solution to the original Google's puzzle. And the answer turned out to be 199,981.
Gregory was overstymied, so he actually wrote a program to solve the puzzle for any non-zero digit. He calculated the beginning of the sequence a(n), where a(n) is the smallest number x > 1 such that the decimal representation of n appears as a substring of the decimal representations of the numbers [1…x] exactly x times.
We already know that a(1) is 199,981. The sequence continues as follows: 199,981, 28,263,827, 372,599,983, 499,999,984, 10,000,000,000, 10,000,000,000, 9,465,000,000, 9,465,000,000, 10,000,000,000, ….
Did you expect this sequence to be increasing? You could have, because smaller numbers tend to contain smaller digits than larger numbers. Then why is the sequence not increasing? As Gregory failed to find a value for the digit 5 below ten billion, he noticed that it's fairly easy to imagine a scenario where you have one less than the number you need, and then the next value has more than you need for equality, and then you equalize again later. In response, Alexey Radul, a friend of one author and a son of the other, suggested a related sequence:
Let a(n) be the smallest number x > 1 such that the decimal representation of n appears as a substring of the decimal representations of the numbers [1…x] more than x times.
The key difference being "more than" rather than "exactly". Starting at 1 then, here are the first nine terms of each sequence:
| n | = | > |
|---|---|---|
| 1 | 199,981 | 199,991 |
| 2 | 28,263,827 | 28,263,828 |
| 3 | 371,599,983 | 371,599,993 |
| 4 | 499,999,984 | 499,999,994 |
| 5 | 10,000,000,000 | 5,555,555,555 |
| 6 | 10,000,000,000 | 6,666,666,666 |
| 7 | 9,465,000,000 | 7,777,777,777 |
| 8 | 9,465,000,000 | 8,888,888,888 |
| 9 | 10,000,000,000 | 9,999,999,999 |
Some of these pairs are interesting in their own right. Notice that 199,991 is ten more than the previously found 199,981. For all the numbers in between, the initial equality holds. Likewise for n=3, each of the numbers between 371,599,983 and 371,599,993 has exactly one three. Hence, the increase in a number by one is the same as the increase in the count of threes. A similar situation holds for n=4.
Gregory has submitted these two new sequences to the Online Encyclopedia of Integer Sequences, as they turned out not to be there yet, and they can be found using the identifiers A163500 for the "=" sequence and A164321 for the ">" sequence. It's not surprising that the values matching this relaxed second condition are more well behaved than those with equality. Do you think the second sequence is always increasing? Wait a minute, let's check that sequence for zero.
In counting zeroes, it is important to remember that we start with one, not zero. In this case the smallest number x such that x is less than or equal to the number of 0s in the decimal representations of [1 … x] is 100,559,404,366. But what is the corresponding number for the "=" sequence? It appears that no such number exists. The challenge of accurately proving it, as they say, is left as an exercise to the reader.
There is no reason that we should be constrained to single digits. The formal statement of the problem provides an obvious generalization, where we consider substrings of each of the numbers [1 … x] rather than digits in those numbers. We should note that we count every occurrence of a substring separately. Thus 11 will be counted twice as a substring of 1113.
We can prove that the "more than" sequence is increasing after the first term. Indeed, for two integers i and j, if i is less than j, then for every occurrence of j, by replacing j with i we get a smaller number with an occurrence of i.
Inspired, Tanya wrote another fancier and faster program to find
values of this sequence for two-digit numbers. Here is the smallest
number x for which the number of "10"s as substrings of the
numbers [1…x] is more than or equal to x. And by a
lucky strike the equality holds. The number is:
109,
The value of a≥(11) might seem like a miracle:
119,
Sadly, a≥(12) is not so pretty:
1,296,624,070,230,872,
We cannot leave off without at least mentioning that the sequence function should next take one more parameter: the base of representation.
We have found only the first few members of these new sequences, and there are many related sequences to be cataloged. We would love to hear tales from your explorations. Enjoy the sequence hunt!
Peter Winkler gave a talk at MIT last fall and, as is customary, the audience was invited to join him for dinner afterwards at a local restaurant. I was eager to dine with Peter because he is a puzzle collector and I was hoping to hear a new puzzle. I got what I was hoping for — tripled. We got a pizza puzzle, a cake puzzle and a tart puzzle to complement our dinner. Today I will discuss the pizza puzzle.
Peter is now a columnist at ACM communications. His column is called "Puzzled" and it is featured as part of the section titled "Last Byte." Writing these paragraphs has made me so hungry that I need to go grab something to bite.
Okay, I am back and here is the pizza puzzle.
Alice and Bob ordered a pizza. The pizza is cut into several radial pieces. Both Alice and Bob are greedy and well-mannered at the same time. They each want to get as much pizza as possible for themselves, but they don't want to be obvious about it. They take pieces in turn, starting with Alice. Because they are well-mannered and not obvious, when it is their turn, they only take a piece that is adjacent to the pieces already taken. Throughout the process of consuming this pizza, the untaken pieces are contiguous.
The question is: Is it possible to cut the pizza in such a way that although Alice starts, Bob can guarantee himself more than half?
If you want to think about this puzzle on your own, now would be a good time to pause. Why? Because in the next paragraph, I will give you some hints about how to approach this question.
If the number of pieces is even, then Alice can't lose. She can number the pieces around the circle consecutively, decide whether all the odd pieces or all the even pieces make up a bigger chunk, and then follow the parity.
But what happens if there are an odd number of pieces? Alice has an advantage, for she will get more pieces. But is that enough to guarantee that she will get at least half? Suppose she starts by taking a minuscule piece. Then Bob can number all of the leftover pieces in order and decide if he prefers the even-numbered group or the odd-numbered group. He is in control now, so he can guarantee himself the bigger part of the leftover pieces.
However, that might not be good enough for Bob to win. For example, if there is a very big piece, one that is bigger than half of the pizza, then in the first move Alice wins.
On the other hand, would Alice necessarily win by starting with the biggest piece?
Suppose the biggest piece is significantly less than half. Would Bob have a chance? To his advantage, he does have a lot of control. He can choose the parity of the pieces he wants at the beginning, and he can also switch this parity later, depending on what Alice does. Does he control the situation enough that it would be possible to cut the pizza in his favor?
I have to add that if you can find a solution with N pieces, then you can easily build a solution with N+2 pieces. Suppose you start with a pizza cut into N pieces, such that Bob will win. If you add two adjacent pieces of zero value to this pizza, you will get a pizza cut into N+2 pieces, such that Bob can still win. Indeed, Bob will follow the strategy he used with the N-pieces pizza, except that each time Alice takes one of the new pieces, Bob takes the other.
Can you find a way to cut a pizza so that Bob can guarantee himself more than half?
I wrote a story a while ago about how a clerk at my previous job mistyped my resignation date, substituting January 2007 for my real date, January 2008. As a result, my medical insurance provider decided that I wasn't covered in 2007, and requested that my doctor return the money he had already received.
After several phone calls my medical insurance was reinstated, but I kept receiving bills from my doctor. When I called my insurance, they assured me that everything was fine and that they had paid my doctor. However, my doctor continued to send me bills.
After half a year of phone calls back and forth, someone finally explained to me what was going on. My insurance company had initially requested the money back. The money was never returned to them, because my doctor's office would not pay them a penny until I had paid the doctor first. In my doctor's database, my visits were marked as unpaid.
When the problem was cleared up, the insurance company stopped requesting that the doctor pay them back. But the computer at my doctor's office didn't understand that stop-the-request command. It didn't know what stopping the request meant.
The computers were talking different languages and I was caught in the middle.
My son, Alexey Radul, made his PhD thesis available to the public.
I was amazed at how much he had invested in the thesis. I assumed that the main goal for a dissertation in computer science is to write a ground-breaking code and that the accompanying text is just a formality. However, this is not the case with my son's thesis. I am not fully qualified to appreciate the "ground-breakness" of his code, but his thesis text is just wonderful.
Alexey decided that he wanted to make his thesis accessible to a wide audience. He had to make a lot of choices and decisions while he was designing and coding his prototype, and in his thesis he devoted a lot of effort to explaining this process. He also tried to entertain: I certainly had fun trying to solve an evil sudoku puzzle on page 87, that turned out not to have a unique solution.
In addition to everything else, Alexey is an amazing writer.
I am a proud mother and as such I am biased. So I'll let his thesis speak for itself. Below is the table of contents accompanied by some quotes:
"Revolution is at hand. The revolution everyone talks about is, of course, the parallel hardware revolution; less noticed but maybe more important, a paradigm shift is also brewing in the structure of programming languages. Perhaps spurred by changes in hardware architecture, we are reaching away from the old, strictly time-bound expression-evaluation paradigm that has carried us so far, and looking for new means of expressiveness not constrained by over-rigid notions of computational time."
"Fortunately, there is a common theme in all these efforts to escape temporal tyranny. The commonality is to organize computation as a network of interconnected machines of some kind, each of which is free to run when it pleases, propagating information around the network as proves possible. The consequence of this freedom is that the structure of the aggregate does not impose an order of time. Instead the implementation, be it a constraint solver, or a logic programming system, or a functional reactive system, or what have you is free to attend to each conceptual machine as it pleases, and allow the order of operations to be determined by the needs of the solution of the problem at hand, rather then the structure of the problem's description."
"Every human harbors mutually inconsistent beliefs: an intelligent person may be committed to the scientific method, and yet have a strong attachment to some superstitious or ritual practices. A person may have a strong belief in the sanctity of all human life, yet also believe that capital punishment is sometimes justified. If we were really logicians this kind of inconsistency would be fatal, because were we to simultaneously believe both propositions P and NOT P then we would have to believe all propositions! Somehow we manage to keep inconsistent beliefs from inhibiting all useful thought. Our personal belief systems appear to be locally consistent, in that there are no contradictions apparent. If we observe inconsistencies we do not crash—we chuckle!"
"This is power. By generalizing propagation to deal with arbitrary partial information structures, we are able to use it with structures that encode the state of the search as well as the usual domain information. We are consequently able to invert the flow of control between search and propagation: instead of the search being on top and calling the propagation when it needs it, the propagation is on top, and bits of search happen as contradictions are discovered. Even better, the structures that track the search are independent modules that just compose with the structures that track the domain information."
"A shift such as from evaluation to propagation is transformative. You have followed me, gentle reader, through 137 pages of discussions, examples, implementations, technicalities, consequences and open problems attendant upon that transformation; sit back now and reflect with me, amid figurative pipe smoke, upon the deepest problems of computation, and the new way they can be seen after one's eyes have been transformed."
"The "concurrency problem" is a bogeyman of the field of computer science that has reached the point of being used to frighten children. The problem is usually stated equivalently to "How do we make computer languages that effectively describe concurrent systems?", where "effectively" is taken to mean "without tripping over our own coattails". This problem statement contains a hidden assumption. Indeed, the concurrency itself is not difficult in the least—the problem comes from trying to maintain the illusion that the events of a concurrent system occur in a particular chronological order."
"Time is nature's way of keeping everything from happening at once; space is nature's way of keeping everything from happening in the same place ( with apologies to Woody Allen, Albert Einstein, and John Archibald Wheeler, to whom variations of this quote are variously attributed)."
"I'm meticulous. I like to dot every i and cross every t. The main text had glossed over a number of details in the interest of space and clarity, so those dots and cross-bars are collected here."
You have been warned. You are allowed to read this if you are 17 or over. Otherwise, you can ask your parents to read this to you. Here is a famous old condom puzzle in the version I heard when I was a teenager myself:
A man hires three prostitutes and wants to have sex with all three of them. They all might have different sexually transmitted diseases and they all want to use condoms. Unluckily, they have only two condoms. Plus, they are in the forest and can't buy new condoms. Can the man have sex with all three of the women without danger to any of the four?
Everyone in this problem is so health-conscious, that it might not be such a dirty problem after all. I leave you with the fun challenge of figuring this problem out.
Another fun variation of this problem is when you have two men and two women and two condoms. Every woman wants to have sex with every man. How can they do that?
If you are a teacher and want to use these great puzzles for younger students, you can follow the example of MathWorld and pretend that it's a glove problem between doctors and patients.
Recently my younger son and his MIT friends invented another variation of this problem:
Suppose three gay men all want to have sex with each other and every pair among them wants to do two penetrative sexual acts, switching roles. They want to avoid contaminating each other, and in addition, each man also does not want to cross-contaminate himself from either region to the other. How can they do that using exactly three condoms?
Let me remind you that they plan to perform six sexual acts altogether, meaning that six condoms would be enough. On the other hand, each of them needs two condom surfaces, so they can't do it with less than three condoms. My son showed to me his solution, but I will postpone its publication.
Of course, you can say that this is a glove problem about three surgeons operating on each other.
In addition, you can generalize it to any number of gay men. Here is my solution for four men and four condoms, where letters denote people, numbers denote condoms, and the order of people represents roles: A12D, B32D, C2D, A14C, B34C, D4C, A1B, B3A, C21B, D41B, C23A, D43A.
Can you solve the problem for five or more people?
I used to receive emails requesting link exchanges with other websites. They promised to increase my page rank by creating additional hyperlinks to my pages. I ignored them. If they thought my website was good, why did they need my reciprocity to link to me? Besides, their websites didn't have anything to do with mathematics; they were the sites of dental services or Honda dealers.
I have resisted the temptation so far. The links that I have on my websites are to sites that I recommend. Sometimes I wonder through other people blogrolls and add good links to my blog.
At other times a blog roll exchange happens: I have Google Analytics installed on my sites. From time to time I examine my traffic. When I see a new traffic flow from a particular website, I check that site out. If I like it, I add it to my blogroll.
I wouldn't mind people writing to inform me that they have a link to my website and asking me if I'd like to reciprocate. But this doesn't happen. Instead, strangers write to me offering to put up a link to my website on the condition that I put a link to them. I do not like this imposition.
Recently I received a request for a blog review exchange. I went to that blog and found that all of its postings were reviews of other people's blogs, presumably those who had agreed on this kind of exchange. I checked out several of those other blogs and I didn't find any of them very interesting.
I missed this opportunity to receive that blog review, but on the other hand, if I start linking to random crap, I might lose the respect of my readers.
My previous paragraph reminded me of a Russian joke:
I wonder how a person whose website comes up first in a Google search for "random crap" feels.
Russians assume that such a person will be embarrassed. They do not understand Americans who welcome negative publicity, and purposefully would name their website randomcraponline.com.
I enjoyed a recent discussion on the sequences fans mailing list. David Wilson suggested an idea for hiding email addresses on webpages from bots: change your email slightly and explain how to change it back.
For example, if you want to contact me, you should reverse my login name in the following email address:
hkaynat@yahoo.com
Or, remove all the digits from the following email address:
1ta2nya3kh4@yahoo.com
Here is a palindrome problem by Nazar Agakhanov from the All-Russian Mathematical Olympiad, 1996:
Can the number obtained by writing the numbers from 1 to n, one after another, be a palindrome?
Of course, we should assume that n > 1.
When I give this problem to my friends, they immediately answer, "No, of course not." The reasoning is simple. The last 9 digits of this palindrome should be 987654321 — all different digits. The earliest you can get these digits at the end of your string 1 to n, is when your number n is actually 987654321. By that time your string of digits is really huge. If we take a random number with 2k digits, then the probability of it being a palindrome is 10(-k). There is no reason to think that writing consecutive integers increases the probability of finding a palindrome. So the probability of hitting a palindrome is so low, that you can safely answer, "No, of course not."
After confidently saying "no", my friends usually stop thinking about the problem altogether. Only my friend David Bernstein suggested a simple solution for this problem. You can try to find the proof, but I do not insist that you do. I am about to give you many other fun problems to solve, and you can choose which ones you want to think about.
Naturally, we can replace the sequence of natural numbers in the Agakhanov's problem with any sequence. So, one problem becomes 160,000 different problems when you plug all current sequences from the Online Encyclopedia of Integer Sequences into it.
For some periodic sequences every concatenation you create is a palindrome. For example, for the sequence of all zeroes, every set of the first n terms is a palindrome. More interestingly, you can think of an increasing sequence such that any first n terms comprise a palindrome, as we see in the sequence of repunits: 1, 11, 111, 1111, etc. Can you think of other sequences like this?
For some sequences, not every concatenation you create is a palindrome, but you can obtain an infinite number of palindromes. One example, suggested by Sergei Bernstein, is the sequence a(n) of the last digit of the greatest power of 2 that divides n. Can you think of other sequences like that?
For some sequences only the initial term itself is a palindrome. Beyond that you can't obtain a palindrome by concatenating the first n terms. For a few of those sequences, this fact is easy to prove. Take, for example, the sequence of powers of ten, or the sequence of squares, or the sequence of prime numbers. Can you think of other similar sequences?
There are many sequences that do not produce a palindrome beyond the first term, even if you try many times. I suspect that they do not, in fact, ever produce a palindrome, but I have no clue how to prove that. I have in mind the sequence of the digits of π. Can you suggest other sequences like that?
Instead of solving the initial problem, I gave you a variety of other problems. My last challenge for you is to find other sequences that can replace the sequence of natural numbers in the Agakhanov's problem so that the problem becomes solvable and the solution is interesting.
The PhD program in Russia was limited to exactly three years. My son Alexey was born right after I started it, and I was distracted from my research for quite some time. At that time, my mom, who lived with us, reached her retirement age of 55. Her retirement would have been supported by the government and her pension would have been almost equal to her salary. So I begged my mom to retire and help me with my son Alexey. I couldn't understand why she wouldn't stop working, so I kept pressing.
At the same time, I was frantically trying to find a place for Alexey in a day care center. I finally was successful, but it backfired. Alexey started getting sick all the time. Daycare was overcrowded, with 30 kids to every adult. Workers didn't have time to attend to every kid. Day care workers were so tired that they were relieved when a few kids stayed home sick.
After Alexey was hospitalized for two weeks with severe dysentery, my mother gave up and retired. It was one year before the end of my graduate school. In that year I wrote four papers and my thesis, and I got my PhD.
Now that I am fifty, I understand that my mother really did love her job. Being older and wiser, I recognize what a sacrifice my mother made in retiring in order to look after a grandchild.
Mom, sorry for being so pushy back then and thank you so much for all that you did for us.

This puzzle was brought to me by Leonid Grinberg.
A frog needs to jump across the street. The time is discrete, and at each successive moment the frog considers whether to jump or not. Unfortunately, the frog has crappy eyesight. He knows there are dangerous cars out there, but he can't see them. If a car appears at the same moment that he decides to jump, he will die.
The adversary sends cars, hoping to kill the frog. The adversary knows the frog's algorithm, but can use only a finite number of cars. The frog wants to maximize his chances of survival with his algorithm. The frog is allowed to use a random number generator that the adversary can't predict. Can you suggest an algorithm for the frog to cross the street and survive with a probability of at least 1 − ε?
My guest blogger is Levy Ulanovsky, a maven of physics puzzles. Here is one of his favorite puzzles:
There are n points in 3-dimensional space. Every point is connected to every other point by a wire of resistance R. What is the resistance between any two of these points?
In 2007 Alexander Shapovalov suggested a very interesting coin problem. Here is the kindergarten version:
You present 100 identical coins to a judge, who knows that among them are either one or two fake coins. All the real coins weigh the same and all the fake coins weigh the same, but the fake coins are lighter than the real ones.
You yourself know that there are exactly two fake coins and you know which ones they are. Can you use a balance scale to convince the judge that there are exactly two fake coins without revealing any information about any particular coin?
To solve this problem, divide the coins into two piles of 50 so that each pile contains exactly one fake coin. Put the piles in the different cups of the scale. The scale will balance, which means that you can't have the total of exactly one fake coin. Moreover, this proves that each group contains exactly one fake coin. But for any particular coin, the judge won't have a clue whether it is real or fake.
The puzzle is solved, and though you do not reveal any information about a particular coin, you still give out some information. I would like to introduce the notion of a revealing coefficient. The revealing coefficient is a portion of information you reveal, in addition to proving that there are exactly two fake coins. Before you weighed them all, any two coins out of 100 could have been the two fakes, so the number of equally probable possibilities was 100 choose 2, which is 5050. After you've weighed them, it became clear that there was one fake in each pile, so the number of possibilities was reduced to 2500. The revealing coefficient shows the portion by which your possibilities have been reduced. In our case, it is (5050 − 2500)/5050, slightly more than one half.
Now that I've explained the kindergarten version, it's time for you to try the elementary version. This problem is the same as above, except that this time you have 99 coins, instead of 100.
Hopefully you've finished that warm-up problem and we can move on to the original Shapovalov's problem, which was designed for high schoolers.
A judge is presented with 100 coins that look the same, knowing that there are two or three fake coins among them. All the real coins weigh the same and all the fake coins weigh the same, but the fake coins are lighter than the real ones.
You yourself know that there are exactly three fake coins and you know which ones they are. Can you use a balance scale to convince the judge that there are exactly three fake coins, without revealing any information about any particular coin?
If you are lazy and do not want to solve this problem, but not too lazy to learn Russian, you can find several solutions to this problem in Russian in an essay by Konstantin Knop.
Your challenge is to solve the original Shapovalov puzzle, and for each solution to calculate the revealing coefficient. The best solution will be the one with the smallest revealing coefficient.
My guest blogger is David Wilson, a fellow fan of sequences. It is a nice exercise to understand how this graph works. When you do, you will discover that you can use this graph to calculate the remainders of numbers modulo 7. Back to David Wilson:
I have attached a picture of a graph.
Write down a number n. Start at the small white node at the bottom of the graph. For each digit d in n, follow d black arrows in a succession, and as you move from one digit to the next, follow 1 white arrow.
For example, if n = 325, follow 3 black arrows, then 1 white arrow, then 2 black arrows, then 1 white arrow, and finally 5 black arrows.
If you end up back at the white node, n is divisible by 7.
Nothing earth-shattering, but I was pleased that the graph was planar.
My son Alexey Radul defended his PhD thesis on Propagation Networks on August 4. Here is the abstract.
I propose a shift in the foundations of computation. Modern programming systems are not expressive enough. The traditional image of a single computer that has global effects on a large memory is too restrictive. The propagation paradigm replaces this with computing by networks of local, independent, stateless machines interconnected with stateful storage cells. It offers great flexibility and expressive power, and has therefore been much studied, but has not yet been tamed for general-purpose computation. The novel insight that should finally permit computing with general-purpose propagation is that a cell should not be seen as storing a value, but as accumulating information about a value.
Various forms of the general idea of propagation have been used with great success for various special purposes; perhaps the most immediate example is constraint propagation in constraint satisfaction systems. This success is evidence both that traditional linear computation is not expressive enough, and that propagation is more expressive. These special-purpose systems, however, are all complex and all different, and neither compose well, nor interoperate well, nor generalize well. A foundational layer is missing.
I present the design of a general-purpose propagation system. I illustrate on several examples how the resulting prototype supports arbitrary computation; recovers the expressivity benefits that have been derived from special-purpose propagation systems in a single general-purpose framework, allowing them to compose and interoperate; and offers further expressive power beyond what we have known in the past.
Warning: this essay contains solutions to math problems.
Here is a famous hat puzzle:
A king decides to give 100 of his wise men a test. If together they pass, they can go free. Otherwise, the king will execute all of them. The test goes as follows: the wise men stand in a line one after another, all facing in the same direction. The king puts either a black or a white hat on each wise man. The wise men can only see the colors of the hats in front of them. In any order they want, each one guesses the color of the hat on his own head. Other than that, the wise men cannot speak. To pass, no more than one of them may guess incorrectly. Given that they have time to agree on a strategy beforehand, how can they assure that they will survive?
Instead of discussing the puzzle above, I'd like to look at a different version. It is an infinite variation of the puzzle that my son Sergei brought back from the Canada/USA Mathcamp last year.
The king has a countable number of wise men. The line starts from the left and is infinite in the right direction. The wise men are all facing to the right and they see the infinite tail of the line. Again, the king places either a black or white hat on each head and they can only say one of two words: black or white. Will they be able to devise a strategy beforehand that ensures that not more than one person makes a mistake?
Oh, I forgot to mention: you are allowed to use the axiom of choice.
Here is the solution. You can build an equivalence relation on the possible placements of hats. To be equivalent, two ways of placing the hats should have the same tail. In other words, there is a person such that both hat arrangements to his right are the same. By the axiom of choice you can pick a representative in any equivalence class. The first wise man looks at all the other hats and calculates in how many places the tail differs from the representative of the class they picked. This is a finite number, and by stating one color or the other, he signals the parity of that number. After that, all the wise men say their colors from left to right. Everyone sees the tail and everyone hears the color choices of the people behind. So every wise man can reconstruct the color of his hat with this information. Only the first person may potentially be mistaken.
Many things about this solution bother me. Where is this country that can fit an infinite number of people? What kind of humans can see into infinity? How much time will this procedure take?
Aside from the practical matters, there are mathematical matters that bother me, too. By the axiom of choice you can pick an element in every class. The problem is that all of the wise men have to pick the same element. The axiom of choice claims the existence of a choice function, which picks an element in each set. So the function exists, but can we distribute this function to many wise men? Remember, they need to agree on this function the night before.
We already implicitly assumed that our wise men have a lot of magical abilities. So we can add to those the ability to go through all the possible tails and memorize the representatives for all the tails in one evening.
But still, I am very curious to know what follows from the axiom of choice. Tell me what you think: does the axiom of choice imply that we can distribute the choice function, or do we need a new axiom? In your opinion, will these wise men live?
I do not know why I like the television show America's Got Talent. Sometimes I picture myself on a stage doing what I love to do the most: entertaining people with mathematics. But it wouldn't really work on the stage of America's Got Talent. The audience makes its judgment in the first five seconds of a performance. There is no way I can teach a new math idea in five seconds.
Back to the show. I especially like the auditions. I noticed a strange correlation between what people say before their performance and what happens on the stage. In short, if a person brags that he/she has the greatest talent and that the judges will be blown away, the performance is likely to be pathetic.
My first thought was that the producers were editing it this way in order to boost the drama of the show. Now I wonder if it could be something else. Perhaps people who do not have much talent need to build up their confidence to appear on the show. And, vice versa, people who have talent can afford to be modest.
I didn't see the same correlation when I watched Britain's Got Talent. Could this tendency be a part of our American culture? After all, the message that confidence is all we need to succeed permeates the whole culture.
A pre-stage interview with one of the contestants on the show was especially telling. She said, "I could be the next greatest act in America, because I have the courage, the self-esteem, the confidence, the faith and hope and belief in myself." Talent wasn't mentioned at all.
Yesterday I had a nightmare. I was on the stage of America's Got Talent and Piers Morgan, my favorite judge, was questioning me:
Piers: Do you have a talent people will pay for?
Me: Yes, I do.
Piers: What is it?
Me: I sing so badly people will pay me to stop.
Do you know that numbers have destinies? Well, to have a destiny, a number needs to have a life, or in mathematical terms, destinies are defined with respect to an operation or a function.
I know the term "destiny" from John Conway, the creator of the Game of Life. It would be harmonious to assume that he suggested this term.
Case 1. SOD. Suppose our function is the sum of digits of a number, denoted as SOD. Then the trajectory of a number k is the sequence a(n), such that a(0) = k and a(n+1) = SOD(a(n)).
Two numbers have the same destiny with respect to SOD if the tails of their trajectories coincide. Suppose a(n) and b(n) are two trajectories. Then the numbers a(0) and b(0) on which these trajectories are build have the same destiny if there exist N and M, such that for any j, a(N+j) = b(M+j). In particular, all numbers in the same trajectory a(n) have the same destiny.
In the above example of SOD, any trajectory of a positive integer ends with a one-digit non-zero number repeating many times. It follows that all the natural numbers have 9 different destinies with respect to SOD, which only depend on the remainder of the number modulo 9.
Given an operation, we can build another sequence that is called "the first occurrence of a new destiny". This is the sequence of numbers c(n) such that c(n) is the smallest number with its destiny. For the SOD operation, the sequence of the first occurrences of new destinies is finite and is equal to: 1, 2, 3, 4, 5, 6, 7, 8, 9.
Case 2. The next prime. Let us consider a different example. Let the function f(n) be the next prime after n. Then wherever we start, the tail of the trajectory with respect to the function f(n) is a sequence of consecutive prime numbers. Therefore, with respect to this function all integers have the same destiny.
Case 3. Reverse. Suppose f(n) is a reverse of n. If a number is a palindrome, then its trajectory is a one-cycle consisting of that number. If a number is not a palindrome, then its trajectory is a two-cycle consisting of a number and its reverse. The first appearance of a new destiny is sequence A131058 — a list of numbers n whose reverse is not less than n. In this case, instead of studying destinies, it might be more interesting to study types of destinies. For this operation we have two types: one-cycles for palindromic integers and two-cycles for non-palindromic integers.
Case 4. The sum of proper divisors. For the next example, let f(n) denote the sum of proper divisors. Let's look at the trajectory of 15: it is 15, 9, 4, 3, 1, 0. The sum of proper divisors of zero is not-defined or is equal to infinity, whichever you prefer. So, let us say the trajectory of 15 is finite, and ends with 1, 0. This situation makes the definition of destinies more complicated, but it is appropriate to say that finite sequences have the same destinies if they end with the same number. For our example of sums of proper divisors all finite sequences end with 0. Thus all the numbers whose trajectories are finite have the same destinies. The sequence of new destinies starts 1, 6, 28, 220, …; and we do not know what the next number is because for 276 we do not know the behavior of its trajectory. Even when we know what kind of life the number is living the destinies are not always clear.
Case 5. TITO. The next interesting example is the TITO operation. TITO is an abbreviation of "Turning Inside, Turning Outside". By definition, to calculate TITO(n) you need to reverse the prime factors of n, multiply them back together (with multiplicities) and reverse the result. For example, to calculate TITO(68), we first find prime factors of 68, which are 2, 2 and 17. We reverse them and multiply: 2*2*71 = 284. Then we reverse the result: TITO(68) = 482.
It is easy to see that prime numbers are among the fixed points of the TITO operation. That means all prime numbers have different destinies of the same type: they end with a one-cycle. There are numbers other than prime that have one-cycle destinies. For example, a palindrome that is a product of palindromic primes is a fixed point of the TITO operation. There are other cases too: for example 26 is a fixed point, but is neither prime nor palindromic. There are numbers that have one-cycle destinies, but are not the fixed points of TITO operation themselves. For example, the trajectory of 49 starts with the following sequence: 49, 94, 841, 4648, 8212, 80041, 415003, 282145, 54796, 849667, 3652951, 35429422, 2941879, 27075955, 5275759, 5275759, 5275759. ….
There are numbers that generate two-cycles. For example, 12 and 156. For numbers n that have only palindromic factors, TITO(n) is equal to the reverse of n. If n is not a palindrome and the reverse of n has only palindromic factors, then the trajectory of n is a two-cycle. Not all two-cycles are like that. Take for example 291 which is a product of primes 3 and 97. Thus, TITO(291) is the reverse of 3*79, which is equal to 732. On the other hand, 732 = 2*2*3*61. Hence, TITO(732) = reverse(2*2*3*16) = 291.
There are longer cycles too. Take for example 15, which generates a cycle of length 7: 15, 51, 312, 447, 3282, 744, 213, 15, …. Also, for some numbers we do not know if there is a cycle. The smallest number for which I myself do not know whether the trajectory tends to infinity or collapses into a cycle is 78.
For the TITO operation we might be more interested in types of destinies. Personally, I am interested not only in the types of destinies, but also in sets of numbers that have the same destinies for the same reasons. For example, I am interested in dividing numbers of one-cycle TITO destinies into three groups: primes, palindromes with palindromic primes and other cases.
Case 6. RATS. I kept the RATS operation for dessert as, in my opinion, it is the most interesting operation with respect to destinies. RATS is the abbreviation of Reverse Add Then Sort. For example, to calculate RATS(732) we need to reverse 732 getting 237, then add 732 and 237 together getting 969, then sort the digits. Thus, RATS(732) = 699.
Let's look at the RATS sequence starting with one: 1, 2, 4, 8, 16, 77, 145, 668, 1345, 6677, 13444, 55778, 133345, 666677, 1333444, 5567777, 12333445, 66666677, 133333444, 556667777, 1233334444, 5566667777, 12333334444, 55666667777, 123333334444, 556666667777, …. We can prove that this sequence is infinite, because numbers fall into a repetitive pattern with an increasing number of digits. This is the first such example in this discussion. John Conway calls the destiny of 1 "the creeper". Conway conjectured that RATS destinies are either the creeper or a cycle.
New destinies do not appear too often in this sequence. That is why the sequence of new destinies might be of interest: 1, 3, 9, 29, 69, 2079, 3999, 6999, 10677, 20169, …. This sequence is A161590 in the Online Encyclopedia of Integer Sequences and it needs more terms. The length of the corresponding periods starting from the second term are: 8, 2, 18, 2, 2, 2, 14, which is the sequence A161593.
Destinies are kinda fun.
Decades ago there was a study in Russia that claimed that a woman worked four more hours a day than a man on average. Men and women were equal in Russia and all had the same 40-hours-a-week jobs. Women were not, by and large, housewives, for they worked full-time.
So where did the additional four hours come from? They were devoted to house chores. In Russia, women did everything at home — at a time when life in Russia was much more difficult. For example, my family didn't have a washer, or a dryer or a dish-washing machine. Plus, everything was in deficit, so to buy milk or a sweater, women had to stand in lines, sometimes for hours.
My mother was very bitter because her husband, my father, never helped her. So I always hoped that when I got married, my husband would take on some of the house chores.
When I married Andrey, he was somewhat helpful — better than the average Russian husband. Then, when I was at grad school, we had a baby named Alexey. Andrey convinced me that I had to take over all the child care because only women could get academic maternity leave. It seemed logical and I agreed.
In a year, when the leave was over, I felt that Andrey should take over some of these duties. He refused. He insisted that since I already had published a paper when I was an undergrad, and since he still didn't have his research results for his PhD, that he had to stay focused on his work. I wasn't strong enough to resist.
We signed up for government child care — private care didn't exist — but we were on the waiting list for a couple of years. Almost no one in Russia — certainly not graduate students — could afford a private babysitter. I couldn't really work on my PhD research because between caring for the house and the baby, I never had big chunks of time. The best I could do was to start preparing for my qualifying exams.
Allow me to digress from my main story for a moment to mention my gray notebook. This notebook was our baby diary. Initially I recorded important baby data — like the first time Alexey smiled. But later, as soon as Alexey turned one year old, he became very eloquent; and this notebook became my son's quote book.
One day Andrey and I went out and my mom babysat Alexey, who was two years old. When we returned, my mother recited the following quote from Alexey:
When will Daddy be back from the university and Mommy from the store?
I don't really remember the long hours in stores or the cooking and cleaning. I remember the quote.

My son Alexey taught me to play "The Settlers of Catan ." This game is so good that throughout the four years of his undergraduate studies, he played it every evening. I am exaggerating of course, but only so slightly. He also taught me some of the game's wisdom.
Lesson 1. Trading is beneficial for both traders.
When you agree to exchange your two rocks for one grain, one grain is more valuable to you than two rocks. The opposite is true for your trading partner.
Presumably, the same principle works for the economy. If I buy a sweater at T.J.Maxx for $20, I need the sweater more than $20. And if the store sells this sweater for $20, they are hoping to make some profit, that is, that the sweater cost them less than $20. Supposedly, shopping transactions are profitable for both parties.
Lesson 2. Trading is bad for non-trading players.
This is the consequence of the fact that in "Settlers of Catan" there is only one winner. If something is good for someone, it is bad for everyone else. In real life you do not have to lose if someone wins. With each shopping transaction everyone gains. This is the reason why shopping must be good for the economy.
Lesson 3. Powerful players can persuade other players to trade against their best interests.
Shortly after I moved to the US, I became very aware of my own smell. My smell didn't change with my move from Russia, nor did my sense of smell change. I was just bombarded with deodorant advertisements, and due to the vulnerability of my self-perception, in one year I bought more deodorants than in all my previous 30 years. I have a friend who has an exceptional sense of smell. He told me that people often use much more deodorant and perfume than they need.
Lesson 4. You pay a lot for storage.
In Settlers, if you have more than seven cards and the dice rolls seven, you need to discard half of your hand. So if you have six cards and someone offers you three grains for one sheep, consider the storage price before jumping into this bargain deal.
Once I bought so much discounted toilet paper that it lasted me for months and months. When it was time to move to a different apartment, I had to pay for the largest truck available to fit all my junk.
Lesson 5. It is important to understand the goal of the person you are trading with.
A profitable deal becomes a big mistake when, as a result of the trade, your trading partner builds a settlement right in the spot where you were planning to build.
Similarly, if your doctor prescribes you a medication, it would behoove you to know whether he will reap any profit from it himself.
Lesson 6. If a player is the only receiver of rock in the game he dictates the price.
This is like a monopoly. I needed my last laptop more than the $1,000 I paid for it. But this price included pre-installed Windows, which I didn't want and which I immediately deleted. I was forced to pay extra for Windows because of Microsoft's monopoly.
So, is shopping good for the economy?
What about that skirt I bought and never used and eventually threw away? I wasted $20 on it. But the store didn't gain that $20; they only gained their profit margin, which could have been $5. That means that together we wasted $15.
I do not throw away every piece of clothing I buy, but it is true that we buy more things than we need.
I think that going shopping to help our country get out of an economic crisis is a ridiculous idea. If you are shopping for other reasons than necessity, you do not help anyone and as a group we lose.
My son Alexey wins almost every game of "Settlers of Catan" he plays. So does my friend Mark Shiffer. The main reason is that they both know how to use trading effectively. To me that indicates that there are probably other people out there who know how to effectively sell deodorants, pills, clothing and other junk to us. I suspect that I lose in every shopping transaction, as I am an unskilled trader. If most folks are like me, could it be that shopping is actually bad for the economy?
Many years ago I conducted an experiment. I asked several sets of friends who had written joint math papers what they thought their individual contributions were. I asked them separately, of course. As the result of this experiment I formulated the conjecture:
The total of what joint authors estimate their contributions to be is always more than 100%.
Here is an actual example of answers I received from the two authors of a joint paper.
Author 1: My contribution is 80%. I suggested a breakthrough idea that made this paper possible. He just typed everything.
Author 2: My contribution is 80%. I did all the work. She just suggested a good idea.
You can see how the answers are synchronized. It is clear that both are telling the truth. People just tend to over-value their own input.
In other cases each author thinks that she or he generated the main idea. It doesn't mean that one of them is lying. Very often they are absolutely sincere. Take this example of Alice and Bob, who are working on a paper together. Alice suggests that they might have better progress on their theorem if they consider graphs with symmetries first. Bob is engrossed in his thoughts and doesn't register Alice's suggestion. Next day, he comes up with an idea to add a group action on graphs. He sincerely believes that this was his own idea. It would be hard to know whether this had been provoked by Alice's suggestion, or had come to Bob independently. Alice assumes that they are working on her idea.
When you acknowledge other people's contribution, keep in mind that their perception might be different from yours. If you do not want to hurt other people's feelings, you might consider inflating your gratitude.
The conjecture doesn't apply to single-author papers. First of all, mathematicians never claim their contribution is 110% as non-mathematicians do. In many cases, especially when there are acknowledgements in the paper, it would be illogical to claim 100% contribution. Most mathematicians are logical, so if they are gracious enough to acknowledge the help of others, they are unlikely to claim 100%.
I would be curious to continue the experiment and either prove or disprove my conjecture. I'd appreciate your help. If you want to be part of this experiment, you can provide the following numbers in your comments: your average contribution to your own papers; and also your weighted average contribution to your joint papers.
I always thought that the famous equation
102 + 112 + 122 = 132 + 142
is sort of a miracle, a random fluke. I enjoyed this cute equation, but never really thought about it seriously. Recently, when my son Sergei came home from MOP, he told me that this equation is not a fluke; and I started thinking.
Suppose we want to find five consecutive integers such that the sum of the squares of the first three is equal to the sum of the squares of the last two. Let us denote the middle number by n, which gives us the equation:
(n–2)2 + (n–1)2 + n2 = (n+1)2 + (n+2)2.
After simplification we get a quadratic equation: n2 – 12n = 0, which has two roots, 0 and 12. Plugging n = 0 into the equation above gives us (–2)2 + (–1)2 + 02 = 12 + 22, which doesn't look like a miracle at all, but rather like a trivial identity. If we replace n with 12, we get the original miracle equation.
If you looked at how the simplifications were done, you might realize that this would work not only with five integers, but with any odd number of consecutive integers. Suppose we want to find 2k+1 consecutive integers, such that the sum of the squares of the first k+1 is equal to the sum of the squares of the last k. Let us denote the middle number by n. Then finding those integers is equivalent to solving the equation: n2 = 2k(k+1)n. This provides us with two solutions: the trivial solution 0, and the non-trivial solution n = 2k(k+1).
So our miracle equation becomes a part of the series. The preceding equation is the well-known Pythagorean triple: 32 + 42 = 52. The next equation is 212 + 222 + 232 +242 = 252 + 262 + 272. The middle numbers in the series are triangular numbers multiplied by four.
Actually, do you know that 102 + 112 + 122 = 132 + 142 = 365, the number of days in a year? Perhaps there are miracles or random flukes after all.
My son, Sergei Bernstein, got accepted to MIT through early action. Because the financial costs of studying at MIT worried me, I insisted that Sergei also apply to Princeton and Harvard, as I had heard they give generous financial packages. In the end, Sergei was rejected by Princeton and wait-listed and finally rejected by Harvard. Though many people have been rejected by Princeton and Harvard, not too many of them have won places on US teams for two different international competitions — one in mathematics and the other in linguistics. To be fair, Sergei was accepted by these teams after Princeton had already rejected him. Nonetheless, Sergei has an impressive mathematical resume:
I am trying to analyze why he was rejected and here are my thoughts.
Many people told me of surprising decisions by Ivy League schools this year. The surprises were in both directions: students admitted to Ivy League colleges who didn't feel they had much of a chance and students not admitted that had every right to expect a positive outcome. I should mention that I personally know some very deserving kids who were admitted.
I wonder if there has been a change in the financial demographics of the students Harvard and Princeton have accepted this year. If so, this will be reflected in the data very soon. We will be able to see if the average SAT scores of students go down relative to the population and previous years.
I do not know why Sergei wasn't accepted; perhaps I'm missing something significant. But if it was because of our finances, it would be ironic: Sergei wasn't admitted to Princeton and Harvard for the same reason he applied there.
I recently got a new job — to coordinate math students at RSI (Research Science Institute). RSI provides a one-month research experience based at MIT for high school juniors. The program is highly competitive and kids from all over the world apply for it.
Before the program started, I asked around among mathematicians for advice on how to do a great job with these talented kids. I was surprised by the conflicting opinions on the value of the program. I thought you'd be interested in hearing those opinions, although I confess that I do not remember who said what, or anyone's exact words. I will just repeat the gist of it.
Former participants:
Potential participants:
Grad students, former and potential mentors:
Professors on the program in general:
I asked some math professors to suggest problems for these students:
The 2009 RSI has just begun. We have awesome students, great mentors and quite interesting problems to solve. I am positive we'll prove the negativists wrong.
Let me remind you of a very interesting problem from my posting Oleg Kryzhanovsky's Problems.
You have 6 coins weighing 1, 2, 3, 4, 5 and 6 grams that look the same, except for their labels. The number (1, 2, 3, 4, 5, 6) on the top of each coin should correspond to its weight. How can you determine whether all the numbers are correct, using the balance scale only twice?
I do not want you to find the weight of each coin; I just want you to say yes if the labels are correct, or no if they are not.
I have given this problem to a lot of people, and not one of them solved it. Some of my students mistakenly thought that they succeeded. For example, they would start by putting the coins labeled 1 and 2 on the left cup of the scale and 3 on the right cup. If these coins balanced, the students assumed that the coins on the left weighed 1 and 2 grams and that the coin on the right weighed 3 grams. But they'd get the same result if they had 1 and 4 on the left, for example, and 5 on the right. I am surprised that no one has solved it yet, as I thought that this problem could be offered to middle-schoolers, since it does not actually require advanced mathematical skills.
If you want to try to solve this problem, pause here, as later in this essay I will be providing a number of hints on how to do it. The problem is fun to solve, so continue reading only if you are sure you're ready to miss out on the pleasure of solving it.
I propose the following sequence a(n). Suppose we have a set of n coins of different weights weighing exactly an integer number of grams from 1 to n. The coins are labeled from 1 to n. The sequence a(n) is the minimum number of weighings we need on a balance scale to confirm that the labels are correct. The original Oleg Kryzhanovsky's problem asks to prove that a(6) = 2. It is easy to see that a(1) = 0, a(2) = 1, a(3) = 2. You will enjoy proving that a(4) = 2 and a(5) = 2.
In general, we can prove that a(n) ≤ n-1. For any k < n, the k-th weighing compares coins labeled k and k+1. If we get the expected result every time, then we can confirm that the weights are increasing according to the labels.
On the other hand, we can prove that a(n) ≥ log3(n). Indeed, suppose we conducted several weighings and confirmed that the labels are correct. To every coin we can assign a sequence of three letters L, R, N, corresponding to where the coin was placed during each weighing — left cup, right cup or no cup. If two coins are assigned the same letters for every weighing, then we can't confirm that the labels on these two coins are accurate. Indeed, if we switch the labels on these two coins, the results of all the weighings will be the same.
My son, Alexey Radul, sent me the proof that a(10) = a(11) = 3. As 3 is the lower bound, we just need to describe the weighings that will work.
Here is the procedure for 10 coins. For the first weighing we put coins labeled 1, 2, 3, and 4 on one side of the scale and the coin labeled 10 on the other. After this weighing, we can divide the coins into three groups (1,2,3,4), (5,6,7,8,9) and (10). We know to which group each coin belongs, but we do not know which coin in the group is which. The second weighing is 1, 5 and 10 on the left, and 8 and 9 on the right. The left side should weigh less than the right side. The only possibility for the left side to weigh less is when the smallest weighing coins from the first and the second group and 10 are on the left, and the two largest weighing coins from the first two groups are on the right. After the second weighing we can divide all coins into groups we know they belong to: (1), (2,3,4), (5), (6,7), (8,9) and (10). The last weighing contains the lowest weighing coin from each non-single-coin group on the left and the largest weighing coin on the right, plus, in order to balance them, the coins whose weights we know. The last weighing is 2+6+8+5 = 4+7+9+1.
Here is Alexey's solution, without explanation, for 11 coins: 1+2+3+4 < 11; 1+2+5+11 = 9+10; 6+9+1+3 = 8 +4+2+5.
Let me denote the n-th triangular number as Tn. Then a(Tn) ≤ a(n) + Tn - n - 1. Proof. The first weighing is 1+2+3 ... +n = Tn. After that we can divide coins into groups, where we know that the labels stay within the group: (1,2,...,n), (n+1,n+2,...,Tn-1), (Tn). We can check the first group in a(n) weighings, the second group in Tn - n - 2 weighings, and we already used one. QED.
Similarly, a(Tn+1) ≤ a(n) + Tn - n.
For non-triangular numbers there are sometimes weighings that divide coins into three groups such that the labels can only be permuted within the same group. For example, with 13 coins, the first weighing could be 1+2+3+4+5+6+7+8 = 11+12+13. After that weighing we can divide all coins into three groups (1,2,3,4,5,6,7,8), (9,10), (11,12,13).
In all the examples so far, each weighing divided all the coins into groups. But this is not necessary. For example, here is Alexey's solution for 9 coins. The first weighing is 1+2+3+4+5 < 7+9. When we have five coins on the left weighing less than two coins on the right, we have several different possibilities of which coins are where. Other than the case above, we can have 1+2+3+4+6 < 8+9 or 1+2+3+4+5 < 8+9. But let's look at the next weighing that Alexey suggests: 1+2+4+7 = 6+8. Or, three coins from the previous weighing's left cup, plus one coin from the previous weighing's right cup equals the sum of the two coins that were left over. This can only be true if the coins in the first weighing were indeed 1+2+3+4+5 on the left and 7+9 on the right. After those two weighings everything divides into groups (1,2,4), (3,5), (6,8), (7) and (9). The last weighing 1+7+9 = 4+5+8, resolves the rest.
To check 7 or 8 coins in three weighings is simpler than the cases for 9, 10, and 11 coins, so I leave it as an exercise. As of today I do not know if it is possible to check 7, 8 or 9 coins in two weighings. Consider this a starred exercise.
I invite you to play with this amusing sequence and calculate some bounds. Also, let me know if you can prove or disprove that this sequence is non-decreasing.
Langton's ant travels on the infinite square grid, colored black and white. At each time step the ant moves one cell forward. The ant's direction changes according to the color of the cell he moves onto. The ant turns 90 degrees left if the cell is white, and 90 degrees right if the cell is black. After that, the cell he is on changes its color to the opposite color.
There is a symmetry of time and space for this ant. If at any point of the ant's travel, someone interferes and reverses the ant's direction in between the cells, the ant and the grid will traverse the steps and stages back to the starting point.
Let's give this ant a life. I mean, let's place him inside the Game of Life invented by John H. Conway. In addition to the Langton's ant's rules, I want the cells to change colors according to the rules of the Game of Life.
Let me remind you of the rules of Conway's Game of Life. We call black cells live cells and white cells dead cells. Black is life and white is death. The cell has eight neighbors — horizontal, vertical, diagonal. At each time step:
So, our ant will be traveling in this dying and reproducing population and correcting nature's mistakes. He revives dead cells and kills live cells.
There is an ambiguity in this ant's life description. The life can happen at two different moments. In the first ant's world, the ant jumps from one cell to the next, and while he is in the air, the cells have time to copulate, give birth and die. Upon landing, the ant changes direction and uses his magic wand to change the life status of its landing cell. In the second ant's world, the ant moves to the destination cell, changes its own direction and the status of the cell and then takes a smoke. All the fun, sex and death happen while he is enjoying his cigarette.
The ant's life has symmetry in a way that is similar to the symmetry of the ant without life. If we reverse the ant's direction back and also switch his life-style from the first to the second or vice versa, then the ant and the grid will go backwards in their states.
The parameters for the Langton's ant were chosen to make the ant's behavior interesting. The parameters of the Game of Life were chosen to make the Game of Life's behavior interesting. To make the ant's life fascinating, we might want to modify the ant's behavior or the Life's rules. The synergy of the ant and the Life might be intriguing only if the ant changes its behavior and the Life changes its rules.
Let's experiment and discover how we need to change the rules in order to make the ant's life interesting.
John H. Conway is teaching me his doomsday algorithm to calculate the day of the week for any day. The first lesson was devoted to 2009. "The 2009's Doomsday is Saturday" is a magic phrase I need to remember.
The doomsday of a particular year is the day of the week on which the last day of February falls. February 28 of 2009 is Saturday, thus 2009's doomsday is Saturday. For leap years it is the day of the week of February 29. We can combine the rules for leap years and non-leap years into one common rule: that the doomsday of a particular year is the day of the week of March 0.
If you know the day of the week of one of the days in 2009, you can theoretically calculate the day of the week of any other day that year. To save yourself time, you can learn by heart all the days of the year that fall on doomsday. That is actually what Conway does, and that is why he is so fast with calculations. The beauty of the algorithm is that the days of the doomsday are almost the same each year. They are the same for all months other than January and February; and in January and February you need to make a small adjustment for a leap year. That gives me hope that after I learn how to calculate days in 2009 I can easily move to any year.
To get us going we do not need to remember all the doomsday days in 2009. It is enough to remember one day for each month. We already know one for February, which works for March too. As there are 28 days in February, January 31 happens on a doomsday. Or January 32 for leap years.
Now we need to choose days for other months that are on doomsday and at the same time are easy to remember. Here is a nice set: 4/4, 6/6, 8/8. 10/10. For even months the days that are the same as the month will work. The reason it works so nicely is that two consecutive months starting with an even-numbered month, excluding February and December, have the sum of days equaling 61. Hence, those two months plus two days are 63, which is divisible by 7.
Remembering one of the doomsdays for every other month might be enough to significantly simplify calculations. But if you want a day for every month, there are additional doomsday days to remember on odd numbered months: 5/9, 9/5, 7/11 and 11/7. These days can be memorized as a mnemonic "9-5 job at 7-11," or, if you prefer, "I do not want to have a 9-5 job at 7-11."
If you throw in March 7, then the rule will fit into a poem John recited to me:
The last of Feb., or of Jan. will do
(Except that in leap years it's Jan. 32).
Then for even months use the month's own day,
And for odd ones add 4, or take it away*.
*According to length or simply remember,
you only subtract for September or November.
Let's see how I calculate the day of the week for my friend's birthday, July 29. The 11th of July falls on the doomsday, hence July 25 must be a doomsday. So we can see that my friend will celebrate on Wednesday this year.
You might ask why I described this trivial example in such detail. The reason is that you might be tempted to subtract 11 from 29, getting 18 and saying that you need to add four days to Saturday. In the method I described the calculation is equivalent, but as a bonus you calculate another day for the doomsday and consequently, you are getting closer to John Conway who remembers all doomsdays.
My homework is the same as your homework: practice calculating the days of the week for 2009.

Visitors to the math department of Princeton University used to stop by John Conway's office. Even if it were closed, they could peek through the window in the door to see the many beautiful, symmetric figures hanging in his office.
The figures, which John Conway had made, were there for 20 years. Just recently John received a letter informing him that his office had been inspected by the State Fire Marshall and that "those things hanging from your ceiling are against the State's fire code and must be taken down." The math department was worried about a possible fine.
So John threw away the "things." I wanted to cry as I watched these huge garbage bags being taken away. I rescued several figures, but that was all that I could fit into my car. For 20 years no one complained, but now the bureaucracy has beat out beauty and mathematics.
This picture is the last view of the "hazardous" office.
On one of my visits to Princeton, I stopped by the math department and, as usual, asked John H. Conway what he was up to. He told me that he was turning numbers inside out. He explained that to perform this procedure on a number you need to reverse every prime factor, multiply the reversed factors back and reverse the result. For example, for 34, which is the product of 2 and 17, we need to reverse 2 and 17 (turning inside), changing them into 2 and 71, multiply back, getting 142, and reversing again (turning outside), leading to the resulting number 241.
He started with a number, turned it inside out, then turned the result inside out, and so on, thus getting an infinite sequence for any number. Every sequence he had calculated up to this point ended with a cycle.
Before I had interrupted him, he was calculating the sequence starting with 78 and it was growing. I suggested that Mathematica could do this calculation faster than John could do in his head. Although that was very rude considering his reputation for speed, John agreed, and we moved to a computer. The computer confirmed that the sequence starting with 78 was growing wildly.
While playing around with this, I became very interested in numbers that are fixed under this turning inside-out operation. First, prime numbers do not change — you just reverse them twice. Second, palindromes with palindromic primes do not change, as every reversal encounters a palindrome to apply itself to. I started to wonder if there are palindromes that are fixed under the turning inside-out procedure, but are not products of palindromic primes.
Here is where John had his revenge. He told me that he would be able to find such a number faster than I could write a program to find it. And he won! He found such a number while I was still trying to debug my program. The number he found was 1226221.
Here is how he beat me. If you have two not-too-big primes that consist of zeroes and ones and that are reversals of each other, their product will be a palindrome. And John is really fast in checking primes for primality. See his lesson in my essay Remember Your Primes.
The next day, when I stumbled on John again, he was doing something else. I asked him about the numbers and he told me that he was no longer interested. Initially he had hoped that every sequence would end in a cycle. The turning inside-out operation doesn't produce much growth in a number. On top of that, prime numbers are stable. That means that if the turning inside-out operation was a random operation with a similar growth pattern, there would have been a very high probability of every sequence eventually hitting a prime. But the operation is not random, as it doesn't change remainders modulo 9. In particular, sequences that start with a composite number divisible by 3 would never hit a prime. Our experiment with 78 discouraged him by showing no hope for a cycle.
I asked him, "Why not do it in binary?" He answered that he had sinned enough playing with a base 10 sequence.
A year later when I next visited Princeton and saw John again, I asked him if he had published or done something with the operation. He had not. He agreed to submit the sequence to the online database, but only if we came up with a name he liked. And we did. We now call this operation TITO (turning inside, turning outside). Please welcome TITO.
When my son Sergei made it to the International Linguistics Olympiad I got very excited. After I calmed down I realized that training for this competition is not easy because it is very difficult to find linguistics puzzles in English. This in turn is because these Olympiads started in the USSR many years ago and were adopted here only recently. So I started translating problems from Russian and designing them myself for my son and his team. For this particular problem I had an ulterior motive. I wanted to remind my son and his team of rare words in English with Greek origins. Here is the problem:
We use many words that have Greek origins, for example: amoral, asymmetric, barometer, chronology, demagogue, dermatology, gynecologist, horoscope, mania, mystic, orthodox, philosophy, photography, polygon, psychology, telegram and telephone. In this puzzle, I assume that you know the meanings of these words. Also, since I am a generous person, I will give you definitions from Answers.com of some additional words derived from Greek. If you do not know these words, you should learn them, as I picked words for this list that gave me at least one million Google results.
In the list below, I picked very rare English words with Greek origins. You can derive the meanings of these words without looking in a dictionary, just by using your knowledge of the Greek words above.
Here are some other words. You do not have enough information in this text to derive their definitions, but you might be able to use your erudition to guess the meaning.
Robert Calderbank and Ingrid Daubechies jointly taught a course called "The Theory of Games" at Princeton University in the spring. When I heard about it I envied the students of Princeton — what a team to learn from!
Here is a glimpse of this course — a problem on Evolutionarily Stable Strategy from their midterm exam with a poem written by Ingrid:
On an island far far away, with wonderful beaches
Lived a star-bellied people of Seuss-imagin'd Sneetches.
Others liked it there too — they loved the beachy smell,
From their boats they would yell "Can we live here as well?"
But it wasn't to be — steadfast was the "No" to the Snootches:
For their name could and would rhyme only with booches …
Until with some Lorxes they came!
These now also enter'd the game;
A momentous change this wrought
As they found, after deep thought.
Can YOU tell me now
How oh yes, how?
In what groupings or factions
Or gaggles and fractions
They all settled down?
Sneetches and Snootches only:
| Sneetches | Snootches | |
| Sneetches | 4 | 3 |
| Snootches | 3 | 2 |
Sneetches and Snootches and Lorxes:
| Sneetches | Snootches | Lorxes | |
| Sneetches | 4 | 3 | 8 |
| Snootches | 3 | 2 | 16 |
| Lorxes | 8 | 16 | -60 |
Find all the ESSes, in both cases.
My guest blogger is a friend and a wordsmith Sue Kelman:
* * *
Rizzo (Ratso to his friends) was my cage mate. We had a nifty pad at Children's Hospital — all we could eat with no scrounging, clean beds, quiet surroundings, and plenty of activity to keep us occupied.
Rizzo's favorite was the maze. Each week he bragged to us about how fast he made it through to the cheese. Larry over in Row-D was always the slowest. All the guys used to razz him about it. No matter how hard he tried, Larry took the wrong turn every time. I think his mother spent some time out at a psych hospital, so maybe they messed with her brain and that affected Larry. Who knows? I suspect that know-it-all visiting researcher from MIT knows what happened to Larry but he's probably keeping it under his hat until he publishes his results in JAMA. Putz!
Okay, so one day, Rizzo just came back from one of those tests where they make us hit a little button when the red and green lights go on. Personally this is my favorite gig because of course there's no running around, but Rizzo likes to throw a monkey wrench into the research data. So every now and then, even when he knows how we should respond, he does just the opposite. I told you, he's one smart rodent.
Rizzo's pretty famous, too. Oh he's not as famous as that talking grey parrot that used to be over at Harvard, but he's been around. For a while he was a top gun — the big performer for a group of genetics guys. He's had his DNA tested more times than Mike Tyson.
Then they lent him out to Hematology where, I swear, the guy's already had 15 blood transfusions. No wonder he's healthy as a horse.
Me, I'm just your average lab rat. I know the drill: wake up, eat a few pellets, perform, eat some more pellets, doze off, and wake up to do it all over again. Not a bad life if you can stay away from those vivisection weirdos. They're like Dr. Mengele all over again.
I'd tell you more but Rizzo's gonna tell us about the time he got out of his cage and made it almost all the way to the Starbucks wagon before they caught him. Great story and he's a real raconteur. None of that Stuart Little crap. We fall over laughing every time we hear it. Gotta go.
Due to the popularity of my previous posting of linguistics puzzles, I've translated some more puzzles from the online book Problems from Linguistics Olympiads 1965-1975. I've kept the same problem number as in the book; and I've used the Unicode encoding for special characters.
Problem 180. Three Tajik sentences in Russian transliteration with their translations are below:
Your task is to assign a meaning to each out of four used Tajik words.
Problem 185. For every sequence of words given below, explain whether it can be used in a grammatically correct English sentence. If it is possible show an example. In the usage there shouldn't be any extra signs between the given words.
Problem 241. In a group of relatives each person is denoted by a lower-case letter and relations by upper-case letters. The relations can be summarized in a table below:
| a | b | c | d | e | f | g | |
| a | — | A | A | B | D | E | E |
| b | A | — | A | E | D | E | E |
| c | F | F | — | G | H | I | I |
| d | H | J | J | — | K | L | L |
| e | B | B | B | N | — | N | N |
| f | O | O | D | L | Q | — | A |
| g | J | J | H | L | K | F | — |
The table should be read as following: if the intersection of the row x and the column y has symbol Z, then x is Z with respect to y. It is known that e is a man.
You task is to find out the meaning of every capital letter in the table (each letter can be represented as one English word).
There is interesting data to show that MIT takes math students more seriously than Harvard and Princeton. By Michael Sipser's suggestion I looked at the Putnam Competition results. Out of the top 74 scorers of 2007, 21 were from MIT, 9 from Harvard and 7 from Princeton. Keep in mind that the total freshman enrollment at MIT is much lower than at Harvard or Princeton. This story repeated itself in 2008: out of top 79 scorers 23 were from MIT, 11 from Harvard and 11 from Princeton.
Ironically, MIT's team didn't win Putnam in those years. MIT's team won the third place after Harvard and Princeton. If you look at the results more closely, you will notice that had MIT arranged teams differently, MIT would have won.
It appears that MIT put their three top scorers from the previous year on their lead team. MIT shouldn't assume that those three continue to be their strongest competitors. Instead they should probably test their students right before the Putnam competition, because if you look at MIT's top individual performers, had they been on a team together, they would have won.
Maybe MIT should rethink its algorithm for creating teams, or maybe we should just wait. As it is obvious that MIT is more serious about math, all top math students may want to go to MIT in coming years. If this happens, the mathematics field will be absolutely dominated by MIT.
Of course you can. Can you do it in Russian? You do not need to know Russian to do it; you just need to solve my puzzle. Below are some numerals written in Russian. You have enough information to write any number from 1 to 99 inclusive in Russian.
If you are too lazy to write all the Russian numerals I requested, try the most difficult ones: 16, 17, 19, 67 and 76.
If you know Russian, then I have a back-up puzzle for you. Do the same thing for French:
And again, if you are lazy, you can concentrate on translating 15, 18, 19, 41, 51, 56, 65, 78 and 99 into French.
I invite my readers to create similar puzzles in all languages.
I recently read an article titled "Think having children will make you happy?" that discusses studies correlating happiness and having children. Some studies show that parents and non-parents have the same level of happiness. But other studies show that non-parents are happier. So, do children make us less happy?
There are two major reasons that kids might make people less happy in a long run. First, children require a lot of resources; they put a strain on our budget, time and careers. As my friend Sue Katz puts it: parental unhappiness could stem from poverty, illness, fighting the educational institutions, feeling stuck in a violent relationship because of the kids — a million things, depending on class and options.
Second, children might not live up to our expectations. Parents often dream that their children will have wonderful careers, be supportive of their parents later in life and most importantly be good people. But in reality, children choose their own careers, not necessarily a path approved by their parents. Plus they might live at a distance or the relationship might be strained. They might even develop completely different values from their parents.
The article claims that on average kids will bring more problems than joy to our lives. Do not rush to cancel unprotected sex with your spouse tonight yet.
My friend Peggy Boning suggested that the study should have separately checked parents who wanted children and parents who didn't. It could be that parents who didn't want children are less happy than parents who wanted them. Which means that if you do not want children, make sure you have protected sex. If you do want children, you might be happier with children than without.
Anyone who has studied statistics knows that correlation doesn't mean causality. An individual who wants to have children might be happier as a result, and at the same time the statistics data may well be true. I'd like to find arguments that can make peace between these two suppositions.
Feel free to add your own ideas.
In Psilvania no one knows English, except for one retired professor Mary Bobs. That is why every year the organizers of the linguistics Olympiad in Psilvania beg Mary to design a puzzle in English. Kids in Psilvania know other languages — which gives individuals an advantage if the puzzle is in those languages. An English puzzle would create a level playing field.
Here is the puzzle that Mary proposed. I'm omitting the Psilvanian text, because the characters do not match anything in Unicode tables.
Professor Bobs provided the following sentences in English, accompanied by their translations into Psilvanian. She called these sentences Raw Materials:
The first task that she required was to translate the following sentences into Psilvanian:
Professor Mary Bobs had quit smoking that very week and she couldn't concentrate. It seems that she may have given more information than is necessary. Is it possible to remove any of the Raw Materials (one or more translated sentences) and keep the puzzle solvable? If so, what is the largest number of Raw Materials you can eliminate? Explain.
Her second task was to translate some sentences from Psilvanian into English, and the answers she hoped the students would calculate were:
For each of the three English sentences above, decide whether the participants of the Olympiad will be capable of getting this particular answer. If for any of these three sentences you suspect that they will not be able to arrive at the correct answer, explain why.
Just out of curiosity I googled two phrases: "male mathematician" and "female mathematician". The results for these phrases on May 3, 2009 were:
Why do you think that female mathematicians are more popular than male mathematicians? I think it is because when people hear the word mathematician, by default they picture a man, so the phrase "male mathematician" is perceived as pleonastic.
I decided to look at some of the 824 sites talking about "male mathematicians". Many web-pages containing the words "male mathematician" are actually pages about female mathematicians, where there is a need to mention a mathematician of the opposite sex. Many other sites are dating pages where a mathematician looks for a partner, and it is wise to start with a description of the sex of the seeker.
Speaking of dating, did I ever mention that I am a female mathematician who was married three times, and all of my spouses were male mathematicians?
One of the best inventions of recent years is toilet seat covers. So whenever I visit a bathroom without seat covers, I curse and make my own out of toilet paper. This is not very effective, as toilet paper doesn't stay nicely in place and it takes a lot of time, when time might be of the essence. Besides it wastes a lot of tissue.
When I come into a toilet and see a lot of long pieces of clean toilet paper lying around, I know that someone else tried to create a seat cover before me.
So here is my idea. Why not make individual packages with folded toilet seat covers, like kleenex packets? When I couldn't find toilet seat covers in my local pharmacy, I started wondering how to patent my idea and dreaming about a lot of money. But before I let myself get too excited, I checked the Internet. My new toilet-seat-covers-to-go were already available. So I bought some. Now, every time I flush them, I watch my potential patent going down the toilet.
I would like to discuss the solution to one of the linguistics puzzles I posted a while ago. Here is problem number 211 from the online book Problems from Linguistics Olympiads 1965-1975:
You are given words in Swahili: mtu, mbuzi, jito, mgeni, jitu and kibuzi. Their translations in a different order are: giant, little goat, guest, goat, person and large river. Make the correspondence.
First, lets say that a giant is a large man. The Swahili translation of "giant" may have elements of Swahili words for a "man" and a "large river". Next we notice that each of these Swahili words naturally divides into two parts. We can put them in a table such that the first part is the same for every row and the second part is the same for every column.
| m-tu | m-buzi | m-geni | |
| ji-tu | ji-to | ||
| ki-buzi |
When I gave this problem to my students, they loved the idea that the word "giant" is comprised of the two words "large" and "man", so they assumed that in Swahili a "guest" would also have a two-part translation, such as a "man who visits." In the list of words we have three different types of "man": man, giant and guest. Once they noticed that "m" appears three times, they concluded that "m" must mean a man. Therefore, the object must be the first part of a Swahili word, while the second part contains its description.
Next, they noted that the first part "ji" appears twice. They decided that "ji" must be a goat and thus "ki" must be a river. All of this gives us sufficient information to derive the translations: "mgeni" a guest, "kibuzi" a large river, "mbuzi" a giant, "mtu" a man, "jitu" a goat and "jito" a little goat.
My students were very proud of themselves, but I was dissatisfied with this solution. Here are the problems I've identified:
I would suggest a different approach. Let's say that the puzzle is about sizes, and we have three objects (man, guest, goat) of normal size, two large objects (giant and large river), and one small object (little goat). That means "m" must mean normal, and the size description is in front. If the first part is the size, then "ki" is small, "ji" large. From here "mgeni" is a guest, "kibuzi" a little goat, "mbuzi" a goat, "mtu" a man, "jitu" a giant, and "jito" is a large river.
I love this puzzle because it teaches us to continue pondering, even after everything seems to fit. If you stumble upon the first solution you need to go back and think some more. Only after you discover the second solution does it become clear that the second one is right.
My son, Alexey Radul, married Rebecca Frankel recently. They had a nerdy wedding. You can judge just how nerdy by this poem written and presented by Gremio (Gregory Marton), the best man:
In this summation, may there be no subtraction;
May you multiply blissfully, and find no division;
May the roots of the power of your love run deep;
May the logs of your joys be exponentially steep;
May you derive greatest pleasure from integrating your lives,
And well past your primes, retain composite rhymes.
This group gathered here, on that lush green field:
May we help you build proofs on the vows you just sealed.
I have a tiny book written by Vladimir Arnold Problems for Kids from 5 to 15. A free online version of this book is available in Russian. The book contains 79 problems, and problem Number 6 criticizes American math education. Here is the translation:
(From an American standardized test) A hypotenuse of a right triangle is 10 inches, and the altitude having the hypotenuse as its base is 6 inches. Find the area of the triangle.
American students solved this problem successfully for 10 years, by providing the "correct" answer: 30 inches squared. However, when Russian students from Moscow tried to solve it, none of them "succeeded". Why?
Arnold has inflated expectations for kids. The book presents the problems according to the increasing order of difficulty, and this suggests that he expects kids under 10 to solve Number 6.
Arnold claimed that every student from Moscow would notice what is wrong with this problem. I can forgive his exaggeration, because I've met such kids. Anyways, I doubt that Arnold ever stumbled upon an average Russian student.
My own fundamental interest is in the state of American math education, so I decided to check his claim concerning American students. I asked my students to calculate the area of the triangle in the above puzzle.
Here are the results of my experiment. Most of them said that the answer is 30. Some of them said that it is 24. In case you're wondering where the 24 is coming from, I can explain. They decided that a right triangle with hypotenuse 10 must have two other legs equal to 8 and 6.
Some of the students got confused, not because they realized that there was a trick, but because they thought the way to calculate the area of the right triangle is to take half the product of its legs. As lengths of legs were not given, they didn't know what to do.
There was one student. Yes, there was one student, who decided that he could calculate the legs of the triangle from the given information and kept wondering why he was getting a negative number under the square root.
You decide for yourself whether there is hope for American math education. Or, if you are a teacher, try running the same experiment yourself. I hope that one day I will hear from you that one of your students, upon reading the problem, immediately said that such a triangle can't exist because the altitude of the right triangle with the hypotenuse as the base can never be bigger than half of the hypotenuse.
A long ago my son Sergei went to the Streamline School Olympiad. Some of the problems were really nice and I asked the organizer, Oleg Kryzhanovsky, where he took the problems from. It seems that he himself supplied all the problems, many of which are his original creations. He told me that he can invent a math Olympiad problem on demand for any level of difficulty on any math topic. No wonder that he is the author of almost all math problems at the Ukraine Olympiad.
The following is a sample of his problems from the Streamline Olympiad. For my own convenience I have chosen problems without figures and equations. Note: I edited some of them.
1998 (8th - 9th grade). Find three numbers such that each of them is a square of the difference of the two others.
1999 (9th - 10th grade). The positive integers 30, 72, and N have a property that the product of any two of them is divisible by the third. What is the smallest possible value of N?
1999 (9th - 10th grade). You have 6 coins weighing 1, 2, 3, 4, 5 and 6 grams that look the same. The number (1, 2, 3, 4, 5, 6) on the top of each coin should correspond to its weight. How can you determine whether all the numbers are correct, using the balance scale only twice?
1999 (11th - 12th grade). In how many ways can the numbers 1, 2, 3, 4, 5, 6 be ordered such that no two consecutive terms have a sum that is divisible by 2 or 3.
2000 (6th - 7th grade). Let A be the least integer such that the sum of all its digits is equal to 2000. Find the left-most digit of A.
2000 (8th grade). You have six bags with coins that look the same. Each bag has an infinite number of coins and all coins in the same bag weigh the same amount. Coins in different bags weigh 1, 2, 3, 4, 5 and 6 grams exactly. There is a label (1, 2, 3, 4, 5, 6) attached to each bag that is supposed to correspond to the weight of the coins in that bag. You have only a balance scale. What is the least number of times do you need to weigh coins in order to confirm that the labels are correct?
I've been translating a lot of linguistics puzzles lately. Now it is my turn to create a new linguistics puzzle. Here are some English phrases with their Russian translations:
Your task is to translate into Russian the following sentences:
Bonus question. Have you noticed any signs that I am getting tired of linguistics?
I stumbled on a Russian linguistics competition called The Russian Little Bear. Most of the puzzles are Russian-specific; but some of them can be translated. I concentrated on puzzles for grades six through nine and used Unicode for uncoding strange characters.
Problem 1. Here are some Latin words with their English translations:
Pick the line of words from A to E that best translates these phrases into Latin: You are loved, I ask, He invites.
Problem 2. The first astronauts from India (I), Hungary (H), France (F) and Germany (G) were Bertalan Farkas (1), Sigmund Jähn (2), Rakesh Sharma (3) and Jean-Loup Chrétien (4). Match the astronauts to the countries:
Problem 3. You do not need to know Russian to solve this puzzle. It is enough to know the modern Russian alphabet: А, Б, В, Г, Д, Е, Ё, Ж, З, И, Й, К, Л, М, Н, О, П, Р, С, Т, У, Ф, Х, Ц, Ч, Ш, Щ, Ъ, Ы, Ь, Э, Ю. Before XVIII century, numbers in Russian were denoted by letters, for example: ТЛЕ — 335, РМД — 144, ФЛВ — 532.
How was 225 written in old Russian?
(A) ВВФ; (B) ВВЕ; (C) СКЕ; (D) СКФ; (E) ВНФ.
Problem 4. Here are several Turkish words and phrases with their English translations:
Pick the line of words from A to E that best translates these phrases into Turkish: thirty isles, men?

Courtney Gibbons gave me her permission to add her webcomics to my collection of Funny Math Pictures.
Abstruse Goose gave me his permission to add his webcomics to my collection of Funny Math Pictures.
Until the introduction of the Abel prize, the Fields medal was the most prestigious prize in mathematics. The medal has been awarded 48 times and all of the recipients have been men. Can we conclude that women are inferior to men when it comes to very advanced mathematics? I do not think so.
The Fields medal was designed for men; it is very female-unfriendly. It is the prize for outstanding achievement made by people under age 40. Most people start their research after graduate school, meaning that people have 10-15 years to reach this outstanding achievement. If a woman wants to have children and devote some time to them, she needs to do it before she is 40. That puts her at a big disadvantage for winning the medal.
Recently the Abel prize for mathematics was introduced. This is the math equivalent of a Nobel prize and nine people have received the prize, all of them male. The Wolf prize is another famous award: 48 people have received it so far and they too have all been male.
On the grand scale of things, women have only recently had the option of having a career in mathematics. Not so long ago it was considered quite exceptional for a woman to work in mathematics. The number of female mathematicians is increasing, but as this is a new trend, they are younger people. At the same time, Abel prizes and Wolf prizes are given to highly accomplished and not-so-young people. That means the increase in the percentage of women PhDs in mathematics might affect the percentage of females getting the prize, but with a delay of several dozen years.
There are other data covering extreme math ability. I refer to the International Math Olympiad. The ability that is needed to succeed in the IMO is very different from the ability required to succeed in math research. But still they are quite similar. The IMO data is more interesting in the sense that the girls who participate are usually not yet distracted by motherhood. So in some sense, the IMO data better represents potential in women's math ability than medals and prizes.
Each important math medal or prize is given to one person a year on average. So the IMO champion would be the equivalent of the Fields medal or the Wolf prize winner. While no girl was the clear best in any particular year, there were several years when girls tied for the best IMO score with several other kids. For example:
In one of those years, a girl might have been the best, but because the problems were too easy, she didn't have a chance to prove it. Evgenia Malinnikova was an outstanding contender who twice had a perfect score. In 1990, she was one out of four people, and she was younger than two of them, as evidenced by the fact they they were not present in 1991. Only one other person — Vincent Lafforgue — got a perfect score in 1990 and 1991. We can safely conclude that Evgenia was one of two best people in 1990, because she was not yet a high school senior.
This might be a good place to boast about my own ranking as IMO Number Two, but frankly, older rankings are not as good as modern ones. Fewer countries were participating 30 years ago, and China, currently the best team, was not yet competing.
Girls came so close to winning the IMO that there is no doubt in my mind that very soon we will see a girl champion. The Fields medal is likely to take more time.
Due to the popularity of my previous posting of linguistics puzzles, I've translated some more puzzles from the online book Problems from Linguistics Olympiads 1965-1975. All of them are from the phonetics section and I've kept the same problem number as in the book. I've used the Unicode encoding for special characters.
Problem 20. In the table below there are numerals from some Polynesian languages. Note that I couldn't find the proper English translation for one of the languages, so I used transliteration from Russian. The language sounds like "Nukuhiva" in Russian.
| Languages | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|
| Hawaiian | kahi | lua | ha | lima | ono | hiku | walu | ***** | ||
| Māori | tahi | rua | toru | wha | ono | whitu | waru | iwa | ***** | |
| Nukuhiva | tahi | to'u | ha | ono | va'u | ***** | ||||
| Rarotongan | ta'i | 'a | rima | ono | 'itu | varu | iva | ŋa'uru | ||
| Samoan | tasi | lua | lima | ono | fitu | iva | ŋafulu |
Your task is to find the words that should be in the empty cells. Note that wh, ', and ŋ denote special consonants.
Problem 21. Below you will find words in several relative languages. You can group these words into pairs or triples of words with the same origin and the same or a similar meaning.
āk, dagr, bōk, leib, fōtr, waʐʐar, buoh, dæʒ, plōgr, hām, wæter, hleifr, pfluog, eih, heimr, fuoʐ, plōʒ.
Task 1. Divide the words into groups so that the first group has words from the same language, the second group has words from another language and so on.
Task 2. (optional) List your suggestions about the meanings of the words and about the identity of the languages.
Problem 22. These words from the Aliutor language are followed by their translations. The stresses are marked by an apostrophe in front of the stressed vowel.
Your task is to put the stresses in the following words: sawat 'lasso', pantawwi 'fur boots', nəktəqin 'solid', ɣətɣan 'late autumn', nəminəm 'bouillon', nirvəqin 'sharp', pujɣən 'spear', tilmətil 'eagle', wiruwir 'red fish', wintatək 'to help', nəmalqin 'good', jaqjaq 'seagull', jatək 'to come', tavitətkən 'I will work', pintətkən 'he attacks (someone)', tajəsqəŋki 'in the evening'.
Note that the vowel ə is similar to many unstressed syllables in English words, such as the second syllable in the words "taken" and "pencil". This vowel is shorter than other vowels in the Aliutor language.
Last time Sue refinanced her mortgage was six years ago. She received a 15-year fixed loan with 5.5% interest. Her monthly payment is $880, and Sue currently owes $38,000.
Sue is considering refinancing. She has been offered a 5-year fixed loan with 4.25% interest. You can check an online mortgage calculator and see that on a loan of $38,000, her monthly payments will be $700. The closing costs are $1,400. Should Sue refinance?
Seems like a no-brainer. The closing costs will be recovered in less than a year, and then the new mortgage payments will be pleasantly smaller than the old ones. In addition, the new mortgage will last five years instead of the nine years left on the old mortgage.
What is wrong with this solution? What fact about Sue's old mortgage did I wickedly neglect to mention? You need to figure that out before you decide whether Sue should really refinance.
So many people liked the puzzles I posted in Subtraction Problems, Russian Style, that I decided to present a similar collection of multiplication and division puzzles. These two sets of puzzles have one thing in common: kids who go for speed over thinking make mistakes.
Humans have 10 fingers on their hands. How many fingers are there on 10 hands?
This one is from my friend Yulia Elkhimova:
Three horses were galloping at 27 miles per hour. What was the speed of one horse?
Here is a similar invention of mine:
Ten kids from Belmont High School went on a tour of Italy. During the tour they visited 20 museums. How many museums did each kid go to?
Another classic:
How many people are there in two pairs of twins, twice?
Can you add more puzzles to this collection?
Today I have my first invited guest blogger, John Berman. John is a 2006, 2007, 2008 and 2009 USAMO qualifier. He was also selected to be on the US team at the Romanian Masters in Mathematics competition. Also, he placed 6th at the North American Computational Linguistics Olympiad. Here is his piece:
The analysis is based on the list of 2009 USAMO qualifiers.
There is a rule that if nobody naturally qualifies for the USAMO from a state, then the highest scoring individual will qualify. Unfortunately, this means that we must remove those states with only one USAMO qualifier. We have 33 states remaining. If we sort these strictly by number of USAMO qualifiers, then we find the following result.
States with at least 4 USAMO qualifiers (24 total) voted for Obama, with the following exceptions: Georgia, Texas, South Carolina, and Missouri. In addition, of the two states with 3 USAMO qualifiers, one voted for Obama and one for McCain. The remaining states with 2 qualifiers (5 total) voted Republican.
Now this is not really unexpected. States with very large populations tend to be democratic and also produce more USAMO qualifiers. The most notable exceptions are Georgia and Texas, both of which were indeed exceptions (major outliers, in fact) above. This prompts the following consideration.
States with at least 8 USAMO qualifiers per 10 million residents (25 total) voted for Obama, with the following exceptions: Florida, Wisconsin, South Carolina, Missouri, and Georgia. Of these, all but Georgia fall within 50% of the target 8 USAMO qualifiers per 10 million residents. Georgia has 18 qualifiers per 10 million residents. Note also that the entire USA has 16 qualifiers per 10 million residents.
Furthermore, if USAMO qualifiers had been used instead of population for determining electoral votes, Obama would have won with 86% of the vote rather than 68%. In general, if the Democrat can secure all those states with at least 1 qualifier per million residents (plus DC), he will win with 303 votes. He can even lose the three red states in that category (Georgia, Missouri, and South Carolina) for exactly 269.
USAMO qualifiers per 10 million residents (for states with more than one qualifier) are:
The states with only one USAMO qualifier are WY, VT, ND, AK, SD, DE, MT, RI, HI, ID, NE, WV, NV, AR, MS, OK, and AZ. The only blue one of these which falls below 8 qualifiers per 10 million is Nevada (we would expect it to have at least 2 qualifiers to fit the expected pattern). Otherwise, it is at least possible that each state fits the pattern of 8 qualifiers per 10 million residents if and only if it votes Democratic.
More than a year ago, when I had my employment benefits with BAE Systems, I called my benefits center with a general question. The customer service representative refused to answer until I gave her my password. I didn't have a password, so she told me that they would mail my new password to me.
But I needed an answer, so I tried the website, only to be informed that my new password is in the mail and I should wait for its arrival.
In a week, a letter with a password arrived and I called the benefits center again. I happily told them my new password and opened my mouth to ask my question. However, they didn't accept my password. Obviously, they had changed my password twice, first when I called and then again when I tried their website. Since only ten minutes passed between these two events, both passwords should have arrived on the same day. But that didn't happen. So my valid password was still in the mail.
In the second it took me to recover from this news, the customer representative told me that they would be sending me a new password and hung up before I could tell her not to.
A new password arrived the next day. I knew that they had already reset that password, and that I'd have to wait a week for the third password to arrive.
I was tempted to call them again and try to create an infinite password resetting loop, but I actually needed to ask my question. So I threw away my freshly arrived, but no-longer-valid password and waited for a week for the next one.
I was lucky to figure it out so quickly, for otherwise my problem could have spiraled out forever. As a professional specifications writer, here are my suggestions to all benefits centers that have that kind of software on what they should do:
I had to wait two weeks to ask a simple question. Now I am writing and complaining about it in the hopes that someone who can fix the problem will read this. Maybe it would have been more productive to write a program that clicks on the "I forgot my password" button every second. This would have daily generated thousands of letters with new passwords to me. Maybe then this problem would have drawn attention sooner.
My son Sergei brought back the Flip-Flop game from Canada/USA Mathcamp, and now I teach it to my students. This game trains students in the multiplication table for seven and eight. These are the most difficult digits in multiplication. This game is appropriate for small kids who just learned the multiplication table, but it is also fun for older kids and adults.
This is a turn-based game. In its primitive simplification kids stand in a circle and count in turn. But it is more interesting than that. Here's what to say and do on your turn, and how the game determines who is next.
First I need to tell you what to say. On your turn, say the next number by default. However, there are exceptions when you have to say something else. And this something else consists of flips and/or flops.
So what are flips? Flip is related to seven. If a number is divisible by seven or has a digit seven, instead of saying this number, we have to say "flip" with multiplicities. For example, instead of 17 we say "flip" because it contains one digit seven. Instead of 14 we say "flip", because it is divisible by seven once. Instead of 7 we say "flip-flip", as it is both divisible by seven and has a digit seven. Instead of 49, we say "flip-flip" as 49 is divisible by the square of seven. Instead of 77 we say "flip-flip-flip" as it has two digits seven and is divisible by seven once.
Flop relates to eight the same way as flip relates to seven. Thus, instead of 16 we say "flop" as it is divisible by eight; instead of 18 we say "flop" as it contains the digit eight; and for 48 we say "flop-flop" as it is both divisible by eight and contains the digit eight.
A number can relate to seven and eight at the same time. For example 28 is divisible by seven and contains the digit eight. Instead of 28 we say "flip-flop". The general rule is that all flips are pronounced before all flops. For example, instead of 788 we will say "flip-flop-flop-flop" as it is divisible by eight and contains the digit seven once and the digit eight twice.
The sequence of natural numbers in the flip-flop version starts as the following: 1, 2, 3, 4, 5, 6, flip-flip, flop-flop, 9, 10, 11, 12, 13, flip, 15, flop, flip, flop, 19, 20, flip, 22, 23, flop, 25, 26, flip, flip-flop, 29, 30, 31, flop, 33, 34, flip, 36, flip, flop, 39, flop, 41, flip, 43, 44, 45, 46, flip, flop-flop, flip-flip, 50, 51, 52, 53, 54, 55, flip-flop, flip, flop, 59, 60, 61, 62, flip, flop-flop, 65, 66, flip, flop, 69, flip-flip, flip, flip-flop, flip, flip, flip, flip, flip-flip-flip, flip-flop, flip, flop-flop, flop, flop, flop, flip-flop, flop, flop, flip-flop, flop-flop-flop, flop, 90, flip, 92, 93, 94, 95, flop, flip, flopflip-flip-flop, 99, 100.
So how does the turn change? Everyone stands in a circle and says their number the way explained above. We start clockwise and move to the next number. For every flip we reverse the direction and for every flop we skip a person. That means that if we have two flips, we don't change the direction, while for two flops we skip two people. If we have flips and flops together, for example 28 corresponds to "flip-flop", then first we change the direction and then we skip a person.
On top of that, there is an extra rule for what you do on your turn. If you say something other than a default number, you switch your position from standing to sitting and vice versa. Sometimes I skip this extra feature — not because I am too lazy to exercise, but because I usually conduct this game in a classroom, where all the desks prevent us from fully enjoying such physical activity.
There are two ways to play this game: as a competition or as practice. When we are competing, a person who makes a mistake drops out. If we're just practicing, no one drops out. Sometimes I am particularly generous and allow my kids one mistake before making them drop out after the second mistake. So far we have played up to 100. I am curious to see if we can ever reach 700 and how long we will be able to continue the game after that.
Testing in the US is dominated by multiple-choice questions. Together with the time limit, this encourages students to stop thinking and go for guessing. I recently wrote an essay AMC, AIME, USAMO Contradiction, in which I complained about the lack of proofs in the first two rounds of math competitions.
Is there a way to improve the situation? I grew up in the USSR, where each round of the math competition had the same format: you were given several hours to write proofs for three or four difficult problems. There are two concerns with organizing a competition in this way. First, the Russian system is much more expensive, whereas the US's multiple choice tests can be inexpensively checked by a computer. Second, the Russian system is prone to unfairness. You need many math teachers to check all these papers on the highest level. Some of these teachers might not be fully qualified, and it is difficult to ensure uniform checking. This system can't easily be adopted in the US. I am surprised I haven't heard of lawsuits challenging USAMO results, but if we were to start having proofs at the AMC level with several hundred thousand participants, we would get into lots of trouble.
An interesting compromise was introduced at the Streamline Olympiad. The problems were multiple choice, but students were also requested to write proofs. Students got two points for a correct multiple choice answer, and if the choice was correct the proof was checked. Students could get up to three points for a correct proof. This idea solves two issues. The writing of proofs is rewarded at an early stage and the work of the judges is not as overwhelming as it would have been, had they needed to check every proof. However, there is one problem that I discussed in previous posts that this method doesn't solve: with multiple choice, minor mistakes cost you the whole problem, even though you might have been very close to a solution. If we want to reward thinking more than accuracy, the proof system allows us to give credit for partial solutions.
I can suggest another approach. If the Russians require proofs for all problems and the Americans don't require proofs for any problem, why not compromise and require a proof for one problem out of the set.
But I actually have a bigger idea in mind. I think that current development in artificial intelligence may soon help us to check the proofs with the aid of a computer. Artificial intelligence is still far from ready to validate that a mathematical text a human has produced constitutes a proof. But in this particular case, we have two things working for us. First, we can use humans and computers together. Second, we do not need to check the validity of any random proof; we need to check the validity of a specific proof of a simple problem that we know in advance, thus allowing us to prepare the computers.
Let us assume that we already can convert student handwriting into computer-legible text or that students write directly in LaTeX.
Here is the plan. Suppose for every problem, we create a database of some sample right, wrong and partial solutions with corresponding scores. The computer checks the students' solutions against the given sample. Hopefully, the computer can recognize small typos and deviations that shouldn't change the point value. If the computer encounters a solution that is significantly different from the ones in the sample, it sends the solution to human judges. Humans decide how to score the solution and the solution and its score is added to the sample database.
For this system to work, computers should be smart enough not to send too many solutions to humans. So how many is too many? My estimate is based on the idea that we wouldn't want the budget of AMC to go too much higher than the USAMO budget. Since USAMO has 500 participants, judges check just a few hundred solutions to any particular problem. With several hundred thousand participants in AMC, the computer would have to be able to cluster all the solutions into not more than a few hundred groups. The judges only have to check one solution in each group.
As a bonus, we can create a system where for a given solution that is not in the database, the computer finds the closest solution and highlights the difference, thus simplifying the human's job.
In order to improve math education, we need to add proofs when teaching math. My idea might also work for SATs and for other tests.
Now that there is more money available for education research, would anyone like to explore this?
A stick has two ends. If you cut off one end, how many ends will the stick have left?
This pre-kindergarten math problem was given to me by Maxim Kazarian who lives in Moscow, Russia. That got me thinking about math education in the US. Actually, just about anything can get me thinking about education in our country. One of our math education patterns is to provide simplified templates and to train kids to plug numbers into them without thinking.
Math education should be about thinking. We need to give kids a lot of math problems that do not fit into standard templates, in order to encourage creative thinking. Here is another puzzle from Maxim:
A square has four corners. If we cut one corner off, how many corners will the remaining figure have?
I invite my readers to invent additional problems that sound as if a subtraction by one is needed, when, in fact, it is not. Here is my contribution:
Anna had two sons. One son grew up and moved away. How many sons does Anna have now?
To get to the national swimming championship, you need to win the state running championships.
What? Is that a joke? Perhaps you're having the same reaction. Because this is exactly what is happening with math competitions. The official USA math competition has three rounds: AMC, AIME and USAMO.
AMC is a multiple-choice competition with 25 problems in 75 minutes. To be good at it, you need speed, accuracy and the ability to guess well.
AIME is 3 hours long and has 15 problems. The problems are a different level of difficulty and guessing will not help you. Though AIME is also multiple-choice, unlike AMC where you choose out of 5, in AIME you choose out of 1,000. But you still need speed and accuracy. A small arithmetic mistake will cost you the whole problem.
USAMO is a competition that runs for 9 hours and has 6 problems. The problems are much harder and you have to write proofs. Proofs? What proofs? Where are the proofs coming from? It is like you got to the national swimming championship because you are a great runner, but you do not know how to swim.
As the result of this system of selection, the USA team at the International Math Olympiad has diverse skills: these kids are good at all three types of the math competitions. It is like taking an Olympic triathlon team to the Olympic swimming event.
However, the US loses by selecting in this way. There are many kids who are great mathematicians: they may be good at difficult problems but not that good at speed-racing problems. An arithmetic mistake costs you only one point at IMO, but a whole problem at AIME. There are kids who are deep mathematicians prone to small arithmetic mistakes. They could get a gold medal at IMO, but they can't pass AMC or AIME.
Not only that. As many AMC problems are boring and do not require ideas, AMC might discourage kids from all math competitions at an early stage.
I will write later with my ideas about how to change AMC. Right now I would like to offer a solution to a smaller problem. I am sure that the US math team organizers know many cases in which a non-senior kid does great at USAMO and is potentially a team member for the next year's US IMO team, but, oops, next year he can't pass AMC.
I suggest the following: USAMO participants are allowed to go to next year's AIME no matter what their AMC scores are. USAMO winners are allowed to go to the next year's USAMO no matter what their AIME results are. This way kids who have proved that they are great swimmers do not need to compete in running again.
I have forgotten all the problems from the math Olympiads I participated in, except for one. That problem cost me one point, and as result I didn't get a perfect score. Here is Problem Number 4 from the 1976 IMO:
Determine the greatest number that is the product of some positive integers, and the sum of these integers is 1976.
The solution goes like this. Consider a partition of 1976. If there is an integer x in the partition greater than 5, then replacing it with two integers x-2 and 2 gives a bigger product. Replacing 4 in the partition by 2 and 2 doesn't change the product. On the other hand, if there is 1 in the partition, it is profitable to attach it to any other number: to replace 1 and x by x+1.
That means the maximum-product partition of a number greater than one has to consist only of twos and threes. If we have three twos in the partition, we can replace them by two threes, thus increasing the product. That means that our partition should consist of twos and threes, and the number of twos shouldn't be greater than three.
I lost my point when I made an elementary arithmetic mistake while calculating the remainder of 1976 modulo 3.
Let's generalize this problem for any number n. If we define the maximum product of partitions a(n) as a function of the number n, we get the sequence A000792 in the Encyclopedia of Integer Sequences. This sequence has other interesting definitions, which appear if we add some structure to partitions of n.
For example, we can suppose that our n is not just a number, but it also represents n objects that are being permuted by the symmetric group Sn. In this case, we can associate some Abelian subgroups of the symmetric group with every partition. Namely, we can divide the set of n elements into disjoint subsets of sizes corresponding to our partition and cycle the elements in every subset. The product of these cycles is an Abelian subgroup, the order of which doesn't depend on how exactly we partition or how we cycle. This order is the product of the partition numbers. It appears that we can get all maximal Abelian subgroups of the symmetric group in this manner. Thus the sequence a(n) is the maximum size of the maximal Abelian subgroup in a symmetric group Sn.
We can do something else with our n objects. Suppose they are represented by vertices of a graph. We take any partition of n and divide our graph into groups of vertices according to this partition. Next we connect vertices of the graph that belong to different groups. If we take a vertex from every group, then the corresponding subgraph is a clique. We can see that it is a maximal clique as two vertices from the same group are never connected and we can't add any more vertices. The number of different cliques of this size is the product of the number of elements in every group. We can prove that a(n) is the maximum possible number of maximal cliques in a graph with n vertices.
Even though I can't return to 1976 to correct my stupid mistake, I love this problem and the corresponding sequence.

A new study is out. Dr. Satoshi Kanazawa blogged about his new discovery. He claims that he can explain why many studies show that men have higher intelligence than women. In his posting Why men are more intelligent than women he posits that intelligence is correlated with height. Taller men on average are smarter than shorter men.
He also claims that given the same height, women are more intelligent than men. As he puts it: "Women who are 5'10'' are on average more intelligent than men who are 5'10''." According to him the only problem women have in the brains department is that they aren't tall enough.
I couldn't find the study itself, only his own announcement. My problem with his study is that, according to Dr. Kanazawa's description, he used data from the National Longitudinal Study of Adolescent Health. If we are talking about adolescents we need to take into account that children grow taller and smarter with age. So any difference in intelligence among the kids of different heights may easily be explained by age. Taller boys may be older and therefore likely to perform better on intelligence tests.
As to intelligence differences between boys and girls of the same height, these girls who are 5'10'' may be from higher grades than boys who are 5'10''.
Some IQ tests are designed to take age into account, but what's totally weird is that a scientist is studying the correlation of intelligence and height, using a population that is in the middle of a physical and mental growth spurt.
As a mathematician, I've been around many people of great intelligence, but I've never perceived bright people as especially tall.
Here is the picture of the USAMO winners for 2007. These are certainly extremely smart kids and I know their heights. The sixth student on the left is my son, Sergei. I personally met all these kids and compared to their peers they are not — except for one boy — especially tall.
How many disjoint letters "O" can you draw on a plane? Clearly, the answer is infinitely many. Now the real question is whether this number can be uncountable. We assume that the letter "O" is just a circle. In this case, if we draw all possible concentric circles, we get an uncountable number of circles. I call letters for which you can build a disjoint uncountable set on the plane stackable letters.
If we do not allow one letter "O" to be drawn inside another, then we can prove that it is not possible to draw more than a countable number of letters "O". Indeed, we can always find a special point inside each letter "O" with both coordinates being rational numbers. As circles do not overlap, no two circles can share the same special point. The set of ordered pairs of rational numbers is countable, thus this set of letters "O" has to be countable.
Now let us move to a more interesting question: how many disjoint letters "T" can you draw on a plane? Let us define the letter "T" as two perpendicular line segments, where the end point of one of the segments is the middle point of the other. Prove that the letter "T" is unstackable.
Can you analyze the whole alphabet for stackability? It doesn't matter which alphabet — you just need to define the drawing of every letter in some reasonable manner.
My real question is, can you define the drawings of English letters in such a way that they are recognizable and the number of stackable letters is maximized? What is the biggest number of letters that you can make stackable?
I brought up this subject to my son Sergei one fine morning. As a result we came up with the following breakfast theorem: Stackable letters are topologically equivalent to a line segment or a circle.
And here is our proof. If the letter in question has a part which is topologically equivalent to "T", then the letter is not stackable, because "T" is not stackable.
Fortunately, or unfortunately, this is not the whole story. The stackability of each letter depends on how you define its shape. There are two groups of letters in the English alphabet that you can make stackable. The first group consists of letters like "V" that can be described as a function on a segment and stacked as a parallel translation of the same letter. The second group, like letter "O", can be described as a function of an angle in polar coordinates, and stacked as a dilation of the same letter.
It is clear that this doesn't cover all cases. For example, a piece of a spiral can be stackable — you stack it by rotating it.
I invite my readers to define two different homeomorphic shapes for the same letter — stackable and unstackable.
I just watched the film Mackenna's Gold for the first time. I would have liked it, if not for the sunrise. It is a treasure-hunting movie with gold lying around in a hidden canyon. The secret entrance to the canyon is revealed by the shadow of a big rock tower at the moment of sunrise.
The problem with this clue is that the azimuth of the sunrise differs depending on the day of the year. For example, at the latitude of Cairo, Tel Aviv or Los Angeles, the sunrise azimuth changes from 116 degrees to 62 degrees as the seasons change. This is more than a 40 degree span!
In any map where directions include a long shadow at sunrise, it should include the day of the year. To be more precise, the trajectory — of a given spot on Earth — around the Sun is not periodic. That means the Sun never rises at the exact same azimuth twice. If we are talking about the approximate azimuth, then the Sun rises in the same region two time periods per year. These periods are mirror reflections of each other, with the winter solstice as their focal point. That means MacKenna and his companions needed to wait for several months for the right moment.
I wonder whether the filmmakers knew about this mistake. I see two possibilities.
The first one is that no one noticed. This is very bad. It confirms that this country is illiterate. In fact, it is worse than that, since you don't really need an education to know that sunrise and sunset happen at different points in the sky depending on the time of year. You just need to look out your window from time to time and pay attention.
The second possibility is that someone noticed, but the filmmakers decided to proceed with it anyway, on the assumption that the audience is too dumb to detect the error. Although there are Internet discussions of goofs in this movie, I was disappointed that I didn't find any complaints about this mistake.
George Lucas borrowed many ideas for the Indiana Jones movies from Mackenna's Gold. In particular, for Raiders of the Lost Ark he borrowed the sunrise mistake without the sunrise itself. In the movie the Sun is supposed to penetrate the crystal in the headpiece of the Staff of Ra and reveal the location of the Well of Souls. To do this, the Staff must be placed in a specific spot in the map room at a certain time of day.
The fact that the poetic idea of a sunrise was removed probably means that they knew that it was a mistake. It was replaced by a non-poetic certain time of day. But they kept the mistake. The Sun doesn't repeat its trajectory every day. Like MacKenna, Indiana Jones would have needed to wait in the map room for several months for the Sun to be in the right spot. George Lucas opted for a fast-paced movie that disregards the laws of physics. The mystery of this movie for me is: Does anyone care?
Romanian Masters in Mathematics might become the most prestigious math competition for high school students. Romania invites teams from the 20 best countries from the previous year's International Math Olympiad. This way they guarantee that all the competitors are extremely strong and they can give more difficult problems than the usual IMO problems.
This year they held their second competition and my son, Sergei Bernstein, was invited to join the USA team. Here is one of the problems:
For a finite set X of positive integers, define ∑(X) as the sum of arctan(1/x) for all elements x in X. Given a finite set S, such that ∑(S) < π/2, prove that there exists a finite set T such that S is a subset of T and ∑(T) = π/2.
The official solution involved a tedious greedy algorithm. My son, Sergei, got an extra point for his unique solution, which was very different from the official one. Here's his solution:
To an integer x we associate a complex number x + i, which in polar coordinates is r(cosθ + i sinθ). Note that θ equals arctan(1/x). That means we can interpret ∑(X) as the angle in the polar form of ∏(x+i) — the product of (x+i) for all x in X.
We are given a set S with elements sj such that ∏(sj+i) has a positive real part, and we need to find other elements tk, such that ∏(sj+i) multiplied by ∏(tk+i) has real part 0.
But we know that the ∏(sj+i) = a + bi, for some integers a and b. I claim that we can always find a positive integer y, so that (a + bi)(y + i) has a smaller real part than a.
Note that ∑(S) < π/2, hence a and b are positive. By an ever so slightly modified version of the division algorithm we can find integers q and r such that b = aq + r, 0 < r ≤ a. Now simply set y equal to q + 1 (which is a positive integer). Then the real part of (a + bi)(y + i) equals ay – b = a – r, and is a non-negative number less than a.
Now we just repeat the process, which obviously has a finite number of steps.
My son's solution wasn't complete. The problem talked about sets of numbers and that implies that the numbers should be distinct. I leave it to my readers to finish this solution for distinct numbers.
This story happened in the summer of 1975. I was 16. Before that, I was naive and brainwashed; by the end of the summer I had grown up. All that summer I was stunned and didn't know what to do as I watched this story unfold.
I was invited to the summer training camp for the International Math Olympiad. There I became friends with a fellow team member Sasha (Alexander) Reznikov. Sasha had dreamed of being a mathematician from childhood. He was gifted and brilliant and when he was in the 7th grade he got noticed by professional mathematicians. They told him that the only way to become a mathematician is to do undergraduate studies at the math department of Moscow State University. He was also told that the math department doesn't accept Jews. Sasha was Jewish.
But there was a hole in the system. If he could get to the International Math Olympiad, he would be admitted to the place of his choice by an order of the Ministry of Education. As the IMO was conducted during entrance exams for universities, there was this special arrangement for the team members. Besides, the Soviet Math Olympiad wasn't yet corrupted, so the Olympiads would give him a chance.
Sasha was brilliant, but he had a disadvantage — he was 2 years younger than his classmates because he had skipped grades. Since the IMO is only for high school students, he had to make it to the IMO before he graduated at 15 years old.
He worked very hard and really pushed himself, and he made it on to our team. The photo of two kids is of Sasha and me that summer.
We had a supervisor — Zoya Ivanovna — who was a Ministry liaison. She was to compile the list of team members for the Ministry of those who should be accepted without entrance exams to universities and colleges. The team had eight people, so every year the list consisted of eight students. That year was special, since we actually only had six people on our team who were high school seniors. Two of us, Sergey Finashin and I, were not yet seniors. But Zoya Ivanovna who was a good-hearted lady decided to sneak in eight people and added our two alternates to the list. As our alternates were preparing for the IMO instead of preparing for entrance exams, this was a generous and fair thing to do. Everything was fine and everyone was happy.

Until one day when strange things started to happen. We were invited for a meeting where Zoya Ivanovna told us that there was a problem with Moscow State University. We were told that the math department has a limit of four people who can be accepted without an entrance exam, and we had five students applying. Zoya Ivanovna asked if there was a volunteer who might reconsider. At this point Alexey Muzykantov said that he would volunteer since he was an alternate. Besides, he was always as interested in physics as in math, and would be happy to study in the physics department.
After the meeting I stumbled upon Zoya Ivanovna crying in the ladies room. She told me that she didn't know what to do. The problem was that out of five people applying for the math department of Moscow State University, three were Jews. Three Jews were too many out of the 400 people annually accepted to the department. Our team coordinator, Valentin Anatolievich Skvortsov, was working at the math department, where he was being pressured. Zoya Ivanovna told me he had been threatened with expulsion from the Communist Party if he didn't reduce the number of Jews by at least one. Being expelled from the Communist Party was a serious threat at that time and Zoya Ivanovna was eager to help, so she invented this idea about the limit. The idea didn't work, because Alexey Muzykantov, who removed himself from the list, wasn't Jewish.
After several days, Sasha Reznikov's mother appeared at the summer program. She told me that she was being pushed to persuade Sasha not to go to Moscow State University.
I asked Zoya Ivanovna why she chose Sasha. She told me that out of the three Jews, one was from Moscow, so she didn't consider him, and Sasha was much younger than the third student and, besides, he had health problems. So she tried to convince Sasha's mother that Sasha would be better off in his home town Kiev than in Moscow.
Sasha went to Kiev University. The system had had a hole through which two Jews passed that year, so even though Sasha had made astonishing efforts, he hit a wall. He was crushed.
Later he tried to transfer to Moscow State University, but was ridiculed, humiliated and denied. Eventually Sasha moved to Israel and got his PhD in mathematics. He died in 2003 by, according to rumors, suicide.
This piece of graph theory was inspired by a logic puzzle The Sexaholics of Truthteller Planet at the 2009 MIT mystery hunt.
Suppose we have a graph where nodes are people and edges connect two people who ever had sex with each other. Given this graph, I am wondering what we can derive about the gender and sexual orientation of the people involved. To do this I need to make some assumptions.
As these are people from another planet, Truthteller, I can choose any assumptions I please, so let us assume that people are of two genders and two types of sexual orientation. The first type of sexual orientation is strictly straight — people of this type only have sex with strictly straight people of the opposite gender. The second type of sexual orientation is strictly homosexual — people of this type only have sex with strictly homosexual people of the same gender. Whoops! I almost forgot: as I assume simplicity, no threesomes happen on that planet.
My question is: Looking at the sex graph can we say anything about sexual orientation? Given any graph, all the vertices can represent homosexual people of the same gender. Is it possible to say, on the other hand, that a vertex of this graph can correspond to a straight person? Let us consider a connected graph representing sex between strictly straight people. This graph has to be bipartite. Hence, given a graph, the maximum number of vertices that correspond to straight people is the total number of vertices in all bipartite connected components.
Similarly, all vertices in a non-bipartite component of a graph are guaranteed to correspond to homosexuals.
Here I would like to name these graphs. If a graph doesn't have a bipartite connected component I will call this graph an all-homosexual graph. The sequence for which the n-th term is the number of all-homosexual graphs with n vertices for n > 0 starts as 0, 0, 1, 3, 16, 96, 812… and is sequence A157016 in the Online Encyclopedia of Integer Sequences. The smallest all-homosexual graph is a complete graph with 3 vertices.
I would like to name not all-homosexual graphs as someone-can-be-straight graphs. The corresponding sequence is A157015.
Thank you to the people who helped me to calculate and clean these two sequences. I received more help with these two sequences than all the sequences I've tried to submit to the Encyclopedia. And it is definitely not because they are about sex, because I purposefully didn't tell them that I was going to relate these sequences to sex. Thanks to Max Alekseyev, Edwin Clark, Brendan McKay and Wouter Meeussen.
You are visiting your girlfriend and she orders pizza. Your evil girlfriend has perfect eyesight and notices fly droppings in three places on the pizza. She is seeking revenge on you for refusing to babysit her poodle and proceeds to cut the pizza. Assuming that the droppings occurred independently and in random places, what is the probability that she will be able to cut a half-circle pizza slice with all three droppings in one half?
Now that I've ruined your appetite, here's a simpler puzzle you can solve as an appetizer to the one I just gave you above. In this puzzle, you have a bread stick that is, of course, in the shape of a line segment. Your girlfriend notices that the bread stick also has three fly droppings on it and she offers to cut an exact half length out of the middle for you. What is the probability that she can cut it so that you end up with all the droppings?
Can you bear to continue this tasty discussion? If so, I'll give you an even simpler problem. Try to solve both of the above puzzles — but with only two droppings instead of three.
If I've spoiled your appetite so completely that you'll skip dinner, why not use the extra time to solve the most challenging of these problems with a meatball that has four fly droppings on it. These droppings, too, are in random places and you must calculate the probability that you are able to cut a semi-sphere with all four droppings on one side.
This final puzzle — in a less distasteful setting — was sent to me by Nick Petry.
I have an old book which I value a great deal. The book is called 200 Problems in Linguistics and Mathematics and only 1,550 copies were printed in 1972. Luckily, a new extended edition just appeared on the web. Both editions are in Russian, so I decided to translate some of the problems into English. Here is a sample:
Problem 1. Here are phrases in Swahili with their English translations:
Translate the following into Swahili:
Problem 2. You are given words in Swahili: mtu, mbuzi, jito, mgeni, jitu and kibuzi. Their translations in a different order are: giant, little goat, guest, goat, person and large river. Make the correspondence.
Problem 3. In Russian the middle name is the patronymic. Thus, the middle initial is the first letter of the father's first name. And, as in many languages, the first initial is the first letter of the first name. Here are names of males in a family:
Draw the family tree of the Petrovs, given that every father has two sons, the patriarch of the family has four grandsons, and his sons have two grandsons each. Prove that the solution is unique.
Problem 4. In Latvian a noun can be one of two genders; furthermore, adjectives agree with nouns in gender, number and case. You are given phrases in either the nominative or the genitive case with their translations:
Indicate which words are nouns and which are adjectives. Divide Latvian nouns into two groups, so that each group contains words of the same gender.
Problem 5. The Portuguese language takes its roots from Latin. In this problem modern Portuguese words are written on the left and their roots (in Latin and other languages on the right). All the words on the left belong to one of three classes: ancient borrowing, early borrowing and late borrowing.
For every Portuguese word, indicate which class it belongs to. (Note that in Portuguese "ch" is pronounced as "sh".)

I bought the book "Math Doesn't Suck: How to Survive Middle School Math Without Losing Your Mind or Breaking a Nail" by Danica McKellar because I couldn't resist the title. Sometimes this book reads like a fashion magazine for girls: celebrities, shopping, diet, love, shoes, boyfriends. At the same time it covers elementary math: fractions, percents and word problems.
You can apply math to anything in life. Certainly you can apply it to fashion and shoes. I liked the parallel between shoes and fractions that Danica used. She compared improper fractions to tennis shoes and mixed numbers to high heels. It is much easier to work with improper fractions, but mixed numbers are far more presentable.
Danica is trying to break the stereotype that girls are not good at math by feeding all the other stereotypes about girls. If you are a typical American girl who hates math and missed some math basics, this book is for you. If you want to discover whether the stars are on your side when you are learning math, the book even includes a math horoscope.

I am celebrating the first hundred essays I have written for my blog. My English teacher and editor Sue Katz edited most of them. Sue Katz not only corrects my English mistakes, but also helps me to choose better and more descriptive words and rearranges my text so that it doesn't sound like a direct translation from Russian.
If you're looking for an editor, she's superb.
Sue is an extremely interesting person. She was one of the first women to gain a black belt in Tae Kwon Do and taught martial arts and dance on three continents. Now she concentrates on her blog and writing. In her blog Sue Katz: Consenting Adult she writes a lot about sex and also about current affairs. She reviews books and movies and expresses her interesting and unique perspective on things. Some of my favorite posts:
I am not only grateful to Sue for the excellent professional job, but also for encouraging me. She laughs at my jokes and is a devoted fan of my blog. Thank you, Sue!
I love "Knights and Knaves" logic puzzles. These are puzzles where knights always tell the truth and knaves always lie. A beautiful variation of such a puzzle with Gnyttes and Mnaivvs was given at the 2009 MIT mystery hunt. In this puzzle people's ability to tell the truth changes during the night depending on the sex partner. You will enjoy figuring out who is a Gnytte or a Mnaivv for each day, who is infected and who slept with whom on each night. Just remember that the ultimate answer to the puzzle is a word or a phrase. So there is one more step after you solve the entire logic part. You do not really need to do this last step, but you might as well. Here we go:
Each inhabitant of Veritas 7, better known as the Truthteller Planet, manifests one of two mutations: Gnytte or Mnaivv. Gnyttes always tell the truth, and Mnaivvs always lie. Once born a Gnytte or Mnaivv, the inhabitant can never change...until now.
Veritas 7 is in the midst of an outbreak of a nasty virus dubbed Nallyums Complex II. If an infected inhabitant has sex with another inhabitant of that planet, each one can be converted from Gnytte to Mnaivv, or Mnaivv to Gnytte, as shown below:
This occurs if either party or both parties have the disease. The disease itself is not transmitted via sex, which is some relief.
Several members of a Veritas 7 village have just contracted Nallyums Complex II. Below are statements from the 15 village residents, taken over the 5-day period since the outbreak. Interviews were taken each morning, and sex occured only at night. Each night, residents paired off to form seven separate copulating couples, with one individual left out. No individual was left out for more than one night.
Can you identify the infected individuals and track their pattern of sexual activity?
A note on wording: If someone refers to sex with someone who was a Gnytte or Mnaivv, they are referring to the individual's truth-telling status just before sex. If a clue says that two individuals had sex, it means they had sex with each other. "Mutation" refers to the individual's current status as Gnytte or Mnaivv.
Security cameras revealed that Jax-7 did not have sex with anyone last night, and that Nebulose and Murgatroid had sex.
Security cameras revealed that Holyoid did not have sex with anyone last night, and that Irono and Oliver had sex.
Security cameras revealed that Dent and Jax-7 had sex.
Security cameras have been vandalized.
I do not remember where I dug this logic puzzle out from:
Folks living in Trueton always tell the truth. Those who live in Lieberg, always lie. People living in Alterborough alternate strictly between truth and lie. One night 911 got a call: "Fire, help!" The operator couldn't identify the phone number, so he asked, "Where are you calling from?" The reply was Lieberg.
Assuming no one had overnight guests from another town, where should the firemen go?
After you have solved this problem, you will see that the sentence "Fire, help!" is true. I wonder, if this statement were a lie, how would we interpret it? It could be that it is just a joke and there is no fire and therefore no need for the police. Or it could be that help is needed — perhaps for a robbery, but not for a fire.
However, when you solve this puzzle, you'll find out that the "Fire, help!" statement is true, so you do not need to wonder what it would mean if the statement were a lie. But I wondered, and as a result I invented several new puzzles.
Here is the first one:
Let's say that people will call the police only if something is happening and there are only two things that could be happening: fire or robbery. Suppose that when people calling the police need to lie, they replace fire with robbery, and vice versa. Suppose also that when asked about location, people will not say, "I am not from Lieberg," as they could have, but will always reply with one word, which is a name of one of three towns. So, there are two possibilities for the first statement — Fire, Help! or Robbery, Help! — and three possible answers to the question about location. — Trueton, Lieberg and Alterborough. My puzzle in this case is: What answer to the location question will give the biggest headache to the police?
We can branch the original puzzle out in a different way. Here is my second puzzle:
We can assume that only fire, not robbery, could happen in this remote place and when people call the police they either say "Fire, help!" or "We do not have a fire, thank you for your time." Let us again assume that people will call the police only if something is happening. In this case, what combinations of first and second sentences of the callers will never happen?
My third puzzle is a more complicated version of the second puzzle:
Let's assume that fires happen with the same probability in every town and that the cost of sending a team of firefighters is identical for every town. Furthermore, the ferocity of all the fires is minuscule and the cost of sending a team is the same, whether or not it turns out that there is a fire. If the police think that the call could have come from several places, they send several teams and the cost multiplies accordingly. The police are obsessed with making charts and the most important number they analyze is the cost they incur, depending on the content of the first sentence of each call.
Given that there are frequent fires, what could the ratio of the cost to police for the calls "Fire, help!" be compared to those that begin with "We do not have a fire, thank you for your time"?
I wanted to see how different presidents affected the Dow Jones index. The index was invented at the end of the nineteenth century, so for my convenience, I will start my analysis from the beginning of the twentieth century. I skipped the presidents who were in office for only four years — four years might not be enough to rebuild a bad economy or to destroy a good one. Besides, in order to give the presidents a fair chance, I compared them for the same time period: eight years.
So I removed from my consideration all those who only served for four years: William Howard Taft, Herbert Hoover, Jimmy Carter and George H.W. Bush. I also combined two presidents together, when one succeeded the other mid-term for a total of eight years. Namely, I combined Warren Harding with Calvin Coolidge, John Kennedy with Lyndon Johnson, and Richard Nixon with Gerald Ford. For Franklin Roosevelt, I only considered the first eight years of his presidency.
Please note that it was not always precisely eight years — the inauguration date was sometimes moved. So Theodore Roosevelt and Harry Truman had slightly less than eight years. I tried to use the Dow Jones index from the exact day of each inauguration, but not all the dates were available in the file I used. So sometimes I had to pick the previous day.
| President | Time | Starting DJI | Ending DJI | Percentage Increase |
|---|---|---|---|---|
| Theodore Roosevelt | Sep 14, 1901 — Mar 4, 1909 | 67.25 | 81.79 | 22% |
| Woodrow Wilson | Mar 4, 1913 — Mar 4, 1921 | 80.71 | 75.11 | -7% |
| Warren Harding/Calvin Coolidge | Mar 4, 1921 — Mar 4, 1929 | 75.11 | 313.86 | 318% |
| Franklin Roosevelt | Mar 4, 1933 — Mar 4, 1941 | 53.84 | 120.88 | 124% |
| Harry Truman | Apr 12, 1945 — Jan 20, 1953 | 158.48 | 288.00 | 82% |
| Dwight Eisenhower | Jan 20, 1953 — Jan 20, 1961 | 288.00 | 634.37 | 120% |
| John Kennedy/Lyndon Johnson | Jan 20, 1961 — Jan 20, 1969 | 634.37 | 931.25 | 47% |
| Richard Nixon/Gerald Ford | Jan 20, 1969 — Jan 20, 1977 | 931.25 | 959.03 | 3% |
| Ronald Reagan | Jan 20, 1981 — Jan 20, 1989 | 950.68 | 2235.36 | 135% |
| Bill Clinton | Jan 20, 1993 — Jan 20, 2001 | 3241.96 | 10587.59 | 227% |
| George W. Bush | Jan 20, 2001 — Jan 20, 2009 | 10587.59 | 7949.09 | -25% |
Some might argue that I need to scale the Dow Jones Index. For example, the inflation rate was very different for different presidents. It is generally accepted that the value of one point in the Dow Jones Index decreases with time, but inflation is only one of many elements contributing to that change. Nonetheless, I took a look at that and the resulting picture didn't change much anyway when I adjusted for inflation.
The Dow Jones is just one number. An increase in the Dow Jones does not completely describe the state of the economy, but it is certainly an interesting measure in its own right.
Let's look at how the presidents and the presidential teams performed, sorting them from best to worst:
| President | Years | Percentage Increase |
|---|---|---|
| Warren Harding/Calvin Coolidge | 1921-1929 | 318% |
| Bill Clinton | 1993-2001 | 227% |
| Ronald Reagan | 1981-1989 | 135% |
| Franklin Roosevelt | 1933-1941 | 124% |
| Dwight Eisenhower | 1953-1961 | 120% |
| Harry Truman | 1945-1953 | 82% |
| John Kennedy/Lyndon Johnson | 1961-1969 | 47% |
| Theodore Roosevelt | 1901-1909 | 22% |
| Richard Nixon/Gerald Ford | 1969-1977 | 3% |
| Woodrow Wilson | 1913-1921 | -7% |
| George W. Bush | 2001-2009 | -25% |
When I started this calculation I expected Clinton to be doing well and Bush badly, I just didn't know exactly how good/bad they were. But the most interesting result of this exercise is the fact that the highest increase in DJI happened right before the Great Depression.
What can I say? I should have done this analysis eight years ago. Maybe the proximity of Clinton's performance to the pre-depression boom could have urged me to move my 401(k) from stocks. Sigh.
The computational linguistics Olympiad started in Moscow in 1962. I first participated when I was in seventh grade. The Olympiad had two sets of problems: the first set was more difficult and meant for seniors, and the second set was for everyone else. Although the sets overlapped, they were significantly different. I should mention that the Soviet Union had 10 grades at that time and prizes were awarded by grade.
I achieved my best result when I was in ninth grade, just below the senior level. During the competition, I solved all the problems for non-seniors and still had a lot of time left. Luckily for me, both sets of problems were in the same booklet, so I proceeded to solve the problems for seniors.
I won two first place prizes: for my ninth grade and for the tenth grade, too.
The following year I was in tenth grade and I felt strange. I couldn't compete on two levels as I was overqualified for non-seniors. So it was impossible to repeat my result. I could only go downhill — winning only one first place in the best case. So, I didn't go to the competition at all.
Someone told me that I was arrogant not to go. But what they didn't know was that I hadn't been able to stop worrying: what if I didn't win first place? All my friends cheered me on during my competitions, and I was afraid to let them down. To this day I can remember my fear of performing worse than the year before.
The organizers of the computational linguistics Olympiad had another reason to think I was arrogant. After my successes, they tried to persuade me to go into linguistics. I actually considered that until someone told me that all the computational linguistics majors are later employed by the KGB. The minute I heard that, I lost all interest in linguistics for many years to come. I told the organizers that all my success was due to my impeccable logic, not to my linguistics ability, so there was no point for me to go into linguistics. My arrogance was reaffirmed.
Recently my son Sergei started to compete in the computational linguistics Olympiad, which reminded me of how interesting linguistics can be. I wonder if Sergei will get a call from the CIA.
Computational Linguistics Olympiads started in Moscow in 1962. Finally in 2007 the US caught up and now we have the NACLO — North American Computational Linguistics Olympiad.
The problems from past Soviet Olympiads are hard to find, so here I present a translation from Russian of a sample problem from the Moscow Linguistics Olympiad website:
You are given sentences in Niuean language with their translations into English:
Translate the following sentences into Niuean:
I was interested for some time in the divisibility of odd Fibonacci numbers. Fibonacci numbers are closely related to Lucas numbers. Lucas numbers Ln follow the same recurrence as Fibonacci numbers: Ln = Ln-1 + Ln-2, but with a different start: L0 = 2, L1 = 1. Obviously, every third Fibonacci and every third Lucas number is even.
Primes that divide odd Lucas numbers divide odd Fibonacci numbers. Let us prove this. Suppose a prime p divides an odd Lucas number Lk, then we can use the famous identity F2k = FkLk. We see that p divides F2k. The fact that Lk is odd means that k is not divisible by 3 and so is 2k. Thus F2k is an odd Fibonacci that is divisible by p.
We see that primes that divide odd Lucas numbers are a subset of primes dividing odd Fibonacci numbers. It is easy to see that it is a proper subset. The smallest prime that divides an odd Fibonacci and doesn't divide any Lucas number is 5.
The next natural question to ask: is there a prime number that divides an odd Fibonacci, doesn't divide an odd Lucas number, but divides an even Lucas number? Below I show that such a prime doesn't exist. In other words, that the set of prime factors of odd Lucas numbers is the intersection of the set of prime factors of odd Fibonacci numbers with the set of prime factors of all Lucas numbers.
Let us consider a Fibonacci-like sequence an in a sense that an = an-1 + an-2 for n > 1. Let me denote by bn, the sequence that is an modulo a prime number p. The sequence bn has to be periodic. It could happen that bn is never 0. For example, Lucas numbers are never divisible by 5. Suppose the sequence bn contains a zero. Let us denote r(p) the difference between the indices of two neighboring zeroes in bn. We can prove that r(p) is well-defined, meaning that is doesn't depend on where you choose your neighboring zeroes. Moreover r(p) doesn't depend on the sequence you start with (see 9 Divides no Odd Fibonacci for the proof). The number r(p) is called the rank of apparition of the prime p.
As the Fibonacci sequence starts with a zero, then the terms divisible by a prime p are exactly the terms with indices that are multiples of the corresponding rank of apparition. The Lucas sequence doesn't start with a zero, but we know that L-n = (-1)nLn. That means, if a Lucas number is ever divisible by a prime p, then the smallest positive index for such a number has to be r(p)/2. Also, the indices of the Lucas numbers divisible by p will be odd multiples of r(p)/2.
We know that the indices of even Fibonacci or Lucas numbers are multiples of 3. Hence, a prime number p that divides an odd Fibonacci number must have a rank of apparition that is not divisible by 3, That means that if p ever divides a Lucas number, then it divides a Lucas number with an index of r(p)/2, which is not divisible by 3, meaning that p divides an odd Lucas number. QED.

My Number Gossip website is becoming very popular. Recently the number of visits increased significantly. I decided to use my Google Analytics software to check the sources of this traffic.
The first spike in visits came after the link to my website appeared on the site PointlessSites.com. Never underestimate bad publicity.
But the real increase was due to the following description of my website at CollegeHumor.com:
Don't even get me started on number 7! Number gossip. All the dirt on your favorite numbers, like 5.
The author of that quote is right. I did dig out some dirt on 5. Prime number 5 is secretly preparing to apply for a Nobel Prize in genetics. It is hiding its two twin brothers, 3 and 7, from the public eye, so that no one will notice that although 3 and 7 are twin brothers of 5, they are not twin brothers of each other. This situation is unique. While 5 has always been a member of two pairs of twin prime brothers, none of the tabloids has picked up on this.
And don't even get me started on number 7! I haven't put it on my website, but everyone knows that 7 is a cannibal, because seven eight nine.
After the link on CollegeHumor appeared, the number of visits jumped 20-fold. The dirt is as good as gold. Maybe I should rethink my approach and put more scandal into my website. Better yet, I should add sex to it. Actually, I already have sex on my website — as part of the word "sextuple".
No, I won't cheapen my numbers just for publicity. I will not add numerical sex positions 69, 71, and 88 to my website. If you're interested in those, check out the cartoon above, which is the work of the famous geek Randall Munroe in his xkcd comic. But he's such a true geek that he doesn't really know what 71 is and probably never heard of 88. (Feel free to call me, Randall.)
My website is about math. I admit that I have sprinkled a few entries on my site that might be considered non-mathematical, but those are my guilty pleasures. Numerical sex positions, however, are not one of them.
Here is a baby puzzle. On Monday the baby said A, on Tuesday AU, on Wednesday AUUA, on Thursday AUUAUAAU. What will she say on Saturday?
You can see that this very gifted baby increases her talking capacity twice each day. The first half of what she says repeats her speech of the day before; and the second half is like the first half, but switches every A and U. If the baby continues indefinitely, her text converges to an infinite sequence that mathematicians call the Thue-Morse sequence (A010060). Of course, mathematicians use zeroes and ones instead of A and U, so the sequence looks like 0110100110010110100….
This sequence has many interesting properties. For example, if you replace every zero by 01 and every one by 10 in the Thue-Morse sequence, you will get the Thue-Morse sequence back. You can see that this is so if you code A in the baby's speech by 01 and U by 10. Thus the Thue-Morse sequence is a fixed point under this substitution. Moreover, the only two fixed points under this substitution are the Thue-Morse sequence and its negation (A010059).
The Thue-Morse sequence possesses many other cool properties. For example, the sequence doesn't contain substrings 000 and 111. Actually any sequence built from the doubles 01 and 10 can't contain the triples 000 and 111 because we switch the digit after every odd-indexed term of such a sequence. A more general and less trivial statement is also true for the Thue-Morse sequence: it doesn't contain any cubes. That is, it doesn't contain XXX, where X is any binary string.
I stumbled upon this sequence when I was playing with evil and odious numbers invented by John H. Conway. A number is evil if the number of ones in its binary expansion is even, and odious if it's odd. We can define a function, called the odiousness of a number, in the following way: odiousness(n) is one, if n is odious and 0 otherwise. We can apply the odiousness function to a sequence of non-negative integers term-wise. Now I can describe the Thue-Morse sequence as the odiousness of the sequence of non-negative numbers. Indeed, the odiousness of the number 2n + k is opposite of the odiousness of k, if k is less than 2n. That means if we already know the odiousness of the numbers below 2n, the next 2n terms of the odiousness sequence is the bitwise negation of the first 2n terms. So odiousness is built the same way as the Thue-Morse sequence, and you can easily check that the initial terms are the same too.
Let me consider as an example the sequence which is the odiousness of triangular numbers A153638: 0, 1, 0, 0, 0, 0, 1, 1, 0, 0, 1, 0…. What can we say about this sequence? We can say that the number of zeroes is infinite, as all the terms with indices of the form 2n-1(2n+1) are zeroes. Also, the number of ones is infinite because all the terms with indices of the form 22n-1(22n-1-1) are ones.
Obviously, we can define the evilness of a number or of a sequence with non-negative terms. Namely, the evilness of a number is 1 if the number is evil, and 0 if it is not. The evilness is the bitwise negation of the odiousness. The evilness of the sequence of non-negative integers is the negation of the Thue-Morse sequence. The odiousness sequence of any sequence of zeroes and ones is the sequence itself, and the evilness sequence is its negation.
I would like to define an inverse odiousness operation on binary sequences. Many different sequences can have the same odiousness sequence. In such a case mathematicians usually define the inverse operation as a minimal non-negative sequence whose odiousness is the given sequence. Obviously, the minimal inverse of a binary sequence is the sequence itself, and thus not very interesting. I suggest that we define the inverse as a minimal increasing sequence. In this case the odiousness inverse of the Thue-Morse sequence is the sequence of non-negative numbers.
For example, let me describe the inverse odiousness of the sequence of all ones. Naturally, all the numbers in the sequence must be odious, and by minimality property this is the sequence of odious numbers A000069: 1, 2, 4, 7, 8, 11, 13, 14, 16, 19…. Analogously, the odiousness inverse of the sequence of all zeroes is the sequence of evil numbers A001969: 0, 3, 5, 6, 9, 10, 12, 15, 17, 18, 20….
Let us find the odiousness inverse of the alternating sequence A000035: 0, 1, 0, 1, 0, 1…. This is the lexicographically smallest sequence of numbers changing putridity. By the way, "putridity" is the term suggested by John Conway to encompass odiousness and evilness the same way as parity encompasses oddness and evenness.
The odiousness inverse of the alternating sequence is the sequence A003159: 0, 1, 3, 4, 5, 7, 9, 11, 12, 13…. By my definition we can describe this sequence as indices of terms of the Thue-Morse sequence that are different from the previous term. This sequence can be described in many other ways. For example, the official definition in the OEIS is that this sequence consists of numbers whose binary expansion ends with an even number of zeroes. It is fun to prove that this is the case. It is also fun to show that this sequence can be built by adding numbers to it that are not doubles of previous terms.
Let us look at the first differences of the previous sequence. This is the sequence A026465: 1, 2, 1, 1, 2, 2, 2, 1, 1, 2, 1, 1, 2, 1, 1, 2… — the length of n-th run of identical symbols in the Thue-Morse sequence. As we know that the Thue-Morse sequence doesn't contain three ones or three zeroes in a row, we can state that the terms of this sequence will continue to be ones or twos.
You can define putridity sequences for any non-negative sequence. Which of them are interesting? I do not know, but I know which of them are not very interesting. For example, the putridity of pronic (oblong) numbers sequence is the same as the putridity of the triangular numbers sequence. This is because pronic numbers are twice triangular numbers and putridity is independent of factors of two. Another uninformative putridity sequence is the odiousness of the powers of two. This sequence consists only of ones.
I bet that my readers can find putridity sequences that are interesting.

I bought Richard a year and a half ago, and I bought him for his looks. Richard is slim, black and shiny. Richard is my first laptop, an HP Pavilion dv2000.
I stopped actively dating a while ago — I am quite happy with my life. So, I named my laptop Richard and he is my everyday male companion. Besides, Richard never complains that I didn't do the dishes; in fact, he never even visits my kitchen.
Recently, Richard died. He just stopped booting. I went to Best Buy to try to fix him, but they told me that I could get a new one for the cost of his likely medical bills.
Why had I gone for the looks? Hadn't I learned this lesson already with my men? This time I got a hold of myself and decided that, for my next laptop, I'm going to ignore looks altogether. My two priorities were reliability and compatibility with my operating system Ubuntu. Everyone suggested Lenovo Thinkpad. I went shopping. Even though Pavilion was still the most attractive, I turned my back on it and bought the Thinkpad.
I decided to name my new laptop Bond, James Bond. Now whenever I'm working, I am actually bonding. And, of course, his looks can be changed. I dressed up James. I gave him striking wallpaper featuring Pierce Brosnan, the most charming James Bond actor. Now James' looks are improved, plus he is very reliable: he aims his weapon at me any time I want — all I need to do is close the windows.
While I was getting acquainted with this new man in my life, I stumbled upon an article about extended warranties from credit cards. Though my HP warranty expired, my extended warranty from the Visa card I used to buy Richard, was still valid. So I went to MicroCenter for a repair estimate. To my surprise it appeared that Richard could be recalled.
I probably should have returned James, but I wasn't absolutely sure that Richard would be resurrected. Besides, I was scheduled to give a talk in Dallas for which I needed a laptop. So I kept James.
In a couple of weeks I got my Richard back. He is alive and well and without any hint of amnesia: no file was lost.
As I sit with my two men on my lap, I think back on all my relationships. I realize that often when I meet a new man, a second one unexpectedly appears in my life. In trying to find a reason for that, I came up with two different explanations:
I have had many problems in my life, especially with men, but I went through two years of psychotherapy and changed my old patterns. I really do not need two men at the same time any more. I am not sure I need one man.
So why on earth did I end up with two laptops? Is this a sign that I need to go back to therapy? Let's hope not. I just need to reject either Richard or James. But, whom?
Richard is an old friend. James is new and more powerful. Unfortunately, both of them are not without character flaws. Richard has energy problems: something is wrong with the battery. And James has communication problems: his wireless card is not working. I have two laptops and neither of them satisfies me fully. Maybe I should go back to therapy after all.
Recently I conducted an experiment. I wrote an essay "What's Hidden?" in which I claimed that the essay had a hidden secret message in it. I coded the message using a very simple method — to read it you need to combine together all the capital letters in the essay.
The goal of the experiment was to audit intelligence agencies of different countries. I wanted to check if this essay would draw any special attention.
Intelligence agencies should crawl around the web and check places that might have secret messages. They might also want to sieve Internet data through some standard coding techniques and check if there are coded messages out there. But the Internet is so vast that most agencies might not have the resources to parse through all the web pages. They probably only analyze suspected pages.
Anyway, I wanted to see if my traffic for this essay would be different from the usual. I have a tool for that — Google Analytics, which provides aggregated geographical data of my traffic. Looking at the results I can see that the visits to this particular essay were mostly from the United States, with a few from Europe. The total number of visits was small, especially compared to my essay on masturbation.
If an intelligence agency has any intelligence it should hide its visits from Google Analytics and crawl around the web without being registered. For example, they can use cached Google pages.
So my intention in this experiment was to check for any agency that had so much time and money on their hands that they were monitoring the entire web and, at the same time, was dumb enough to leave a trail. I am happy to conclude that there is no such agency, with only one potential exception: my home country — the United States.
Disclaimer. I chose the jokes for analysis, not for entertainment. Some of them might be unpleasant to read. Proceed at your own risk.
Russians love jokes and especially politically incorrect ones. They have anecdotes about many nations, but when I was growing up back in Russia, Americans were treated nicely in these jokes. Americans were used as a background for Russians to laugh at themselves. Here is a very old joke about Russian political realities; this was the version that was told during Jimmy Carter's presidency:
A Russian and an American are discussing freedom of speech. The American says, "We have freedom of speech. I can stand in front of the White House and shout that Jimmy Carter is an idiot and nothing will happen to me.c
The Russian replies, "I can also stand in front of the Kremlin and shout that Jimmy Carter is an idiot and nothing will happen to me either."
Or this joke about harsh living conditions:
A Russian and an American describe their houses to each other. The American says, "I have a modest house, three bedrooms, a dining room, a living room, a family room, a kitchen, and a guest room."
The Russian replies, "I have the same thing, just without the inner walls."
The following old joke is becoming less and less amusing as the airline service in America increasingly resembles what Russians have always had:
An American is flying on a Russian flight. A beautiful stewardess approaches him and asks, "Would you like to have dinner?"
The American replies, "What are my choices?"
"Yes or No."
What I am interested to learn from these jokes is whether Russia was preparing for a war with the US during the cold war period. In most cultures, killing a person is a bad thing to do. That means you need an argument to give to solders when you're asking them to kill other people. Usually governments are not proposing that killing is a good thing to do in general, but rather rationalizing why this particular enemy needs to be killed. For example:
Looking at Russian jokes from that period, it's clear that they weren't trying to turn Russians against Americans. I therefore conclude that the USSR was not preparing an open attack on the US. Except in the case of a defensive war, one country planning to attack another would need to employ a process of preliminary distancing from their enemy.
The USSR government was capable of manipulating the populace to think that a war is a defensive war when in reality it was initiated by Russia. But no matter how treacherous they were, it would have been difficult to stage this trick across an ocean. My conclusion is that the USSR wasn't really preparing any open attacks on the US. The whole cold war was a waste of energy, money and resources on both sides.
Now let's move to modern times. There are still some American jokes in which Russians are laughing at themselves. For example, this one reminds us of the fate of Mikhail Khodorkovsky:
Question: Name the question to which Americans would answer "Sure!" and Russians "God, no!"
Answer: Would you like to change places with the richest person in the country?
The following joke appeared several years ago, and at first I classified it as Russians being over-proud of themselves:
"Can you describe a math department at an American university?"
"Yes, this is a place where Russian professors teach Chinese students."
This situation changed recently. It moved from Russians being proud of their math traditions to stereotyping Americans as complete idiots. Here is a very recent joke:
Question: What do you call an intelligent person in the US?
Answer: A tourist.
Here is another joke that assumes complete cluelessness of Americans in geography and history:
Question: How do you recognize an American?
Answer: He is proud that the US won the Vietnam war with Hitler in Iraq.
Not only is the stereotype of Americans that they are stupid, but that they are stupider than everyone else:
Question: Dad, why Americans say "eighteen-ninety three" instead of "one thousand eight hundred ninety three"?
Answer: They still have eight-bit processors in their heads.
The situation with jokes about Americans is getting much worse in Russia. There are so many jokes about Americans that many joke websites formed a special category for American jokes. The speed at which the folklore changed from neutral to offensive was very fast. There is no doubt that it is supported from above. It is very useful for the Russian government to redirect the minds of their citizens from internal problems. Americans serve as a scapegoat.
Another thing Russians laugh a lot about is the idea of political correctness:
The new politically correct rules for chess in the US allowed blacks to make the first move.
Of course, a particular anecdote might not reflect the common opinion or, for that matter, the majority opinion. What is interesting is that there is a new trend. Here is a joke about consumerism:
Do you know that according to the latest American research the average speed of a woman walking around a shopping mall is $200 an hour?
The sad part is that the laugh about consumerism extends to a vision of the US government as being completely corrupt:
US — the government of the money, by the money, for the money.
Of course many jokes originated here and were translated from English. It is interesting which ones Russians chose to translate into Russian:
CNN said that after the war, there is a plan to divide Iraq into three parts … regular, premium and unleaded.
I do think that this newly found hatred comes from Putin and the present Russian administration. Russians are very much against the invasion of Iraq and many anecdotes reflect that:
Question: Mr. President, can you prove that Iraq has weapons of mass destruction?
Answer: Yes. We kept the receipts.
In general, the US is perceived as an aggressor.
George Bush found a way to invade every country — he declared war on Gypsies.
Is Russia preparing for war with the US? I do not know. Such a war seems like a ridiculous idea, but if you look at present-day anecdotes, it seems like Russia is doing more preparation than it did during the cold war period. First, Russia has been finding things to blame Americans for:
— What is the most powerful American chemical weapon?
— McDonalds.
Second, Russians are distancing themselves from Americans. Here is a very recent joke, where for the first time I saw that Americans are called "those people":
Wild turkeys saved pilgrims from hunger. To commemorate this event, every year Americans kill and eat millions of turkeys as a thank you. God save us from doing anything good for those people.
For a long time I have checked the Russian joke websites before I go to bed. But in the last couple of years, I have become uncomfortable with the increasing antagonism towards America, so I decided to write this piece. Now that I finished it, I realized that, it's sad, but we deserve many of the jokes.
I ran an experiment. I copied multiple choices from the 2007 AMC 8 into a file and asked my son Sergei to try to guess the answers, looking only at the choices. I allowed him to keep several choices. The score I assigned depended on the number of leftover choices. If the leftover choices didn't contain the right answer, the score for the problem was zero. Otherwise, it was scaled according to the number of choices he left. For example, if he had four choices left and the right answer was among them he got 1/4 of a point. Here are the choices:
It is clear that if you keep all choices, your score will be 5, which is the expected score for AMC if you are randomly guessing the answers. Sergei's total score was 7.77, which is noticeably better than the expected 5.
There were two questions where Sergei felt that he knew the answer exactly. First was question number two with choices: 2/5, 1/2, 5/4, 5/3, 5/2. All but one of the choices has a 5 in it, so 1/2 must be wrong. Numbers 2/5 and 5/2 are inverses of each other, so if organizers expect you to make a mistake by inverting the right answer, then one of these choices must be the right answer. But 5/4 and 5/3 are better suited as a miscalculation of 5/2, than of 2/5. His choice was 5/2, and it was correct. The second question for which he was sure of the answer was question 19, with his answer 79. I still do not have a clue why.
Sergei's result wasn't too much better than just guessing. That means that AMC 8 organizers do a reasonably good job of hiding the real answer. You can try it at home and see if you can improve on Sergei's result. I will publish the right answers as a comment to this essay in a week or so.
Last revised October 2013