
This blog has a modern version at http://blog.tanyakhovanova.com/, where you can leave comments. This page contains the copies of 94 blog entries for 2010. The latest essays are at http://www.tanyakhovanova.com/MathBlog.html
* * *
A note posted on the door of the tech-support department:
"Theory — you know everything, but nothing works. Practice — everything works, but nobody knows why. In our department we merge theory with practice: nothing works and nobody knows why.
* * *
A plus is two minuses at each others' throats.
I was teaching my students PIE, the Principle of Inclusion and Exclusion. This was the last lesson of 2010 and it seemed natural to have a party and bring some pie. It appears that the school has a new rule. If I want to bring any food to class, I need to submit a request that includes all food ingredients. The administrators send it to the parents asking them to sign a permission slip and then, if I receive all the slips back in time, I can bring pie to school. We had to study PIE without pie.
Our most important task as parents and teachers is to teach kids to make their own decisions. They are in high school; they know by now about their own allergies and diets; they should be able to avoid foods that might do them harm. I understand why schools create such rules, but we are treating the students like small children. We can't protect them forever; they need to learn to protect themselves.
Next semester, we will study the mathematics of fair division. I will have to teach them how to cut a cake without a cake.
I once wrote a story about a mistake that my medical insurance CIGNA made. They had a typo in the year of the end date of my insurance coverage in their system. As a result of this error, they mistakenly thought they had paid my doctors after my insurance had expired and tried to get their money back. While I was trying to correct all this mess, an interesting thing happened.
To help me explain, check out the following portion of my bill. (If it looks a bit funny, it's because I cut out some details including the doctor's name).

On the bill you can see that I had a mammography for which I was charged $493.00, but CIGNA paid only $295.80. The remaining $197.20 was removed from the bill as an adjustment, as frequently happens because of certain agreements between doctors and insurance companies. A year later when CIGNA made their mistake, they requested that the payment be returned. You can see on the bill that once the payment was reversed, my doctors reversed the adjustment too.
When CIGNA fixed the typo, they repaid the doctors, but the adjustment stayed on the bill, which the doctors then wanted me to pay. And that was only one of many such bills. It took me a year of phone calls to get the adjustments taken off, but this is not what I am writing about today.
If not for this mistake, I would have never seen these bills and the revealing information on the different amounts doctors charge to different parties, and how much they really expect to receive. As you can see my doctors wanted 67% more for my mammogram than they later agreed to.
The difference in numbers for my blood test was even more impressive. I was charged $173.00, and the insurance company paid $30.28 — almost six times less.
If I ever need a doctor and I don't have insurance, I will take these bills with me to support my request for a discount. I do not mind if you use this article for the same purpose.

I met Ed (Edik) Frenkel 20 years ago at Harvard when he was a brilliant math student of my now ex-husband, and a handsome young man. Now, at 42, he is a math professor at Berkeley and he is even hotter. He made a bizarre move for a mathematician: he produced and starred in an erotic short movie, Rites of Love and Math. If he wants to be known as the sexiest male mathematician alive, he just might get the title.
The movie created a controversy when Mathematical Sciences Research Institute (MSRI) withdrew its sponsorship for the first screening after a lot of objections based on the trailer. My interest was piqued by a painting that dominated the visual of the trailer's erotica scene. The black and white amateur painting is of the integral sign with Russian letters stylized as math symbols that spell the word "Truth". In addition, the name of the woman in the movie, Mariko, means "truth" in Japanese. Though it felt pretentious, I was hoping that the movie would be symbolic. When I heard that the actors do not talk in the movie, my expectations of symbolism grew. I love movies that are open to interpretation. So I bought the movie, watched it and wrote the following review. Before getting to the review itself I would like to thank Ed Frenkel for sending me the photos and giving me permission to use them in my frank assessment of his work.
Here is the plot:
A Mathematician, hoping to serve humanity, discovers a formula of Love. Bad guys find an evil way to use the formula to destroy humanity and are hunting for the Mathematician, who is hiding in his lover Mariko's home. The Mathematician fears for his own life. Although it would make sense to destroy all the papers with the formula, the Mathematician loves his formula even more than his lover and himself. He wants to preserve the formula and tattoos it on her body with her consent.
There is much about the film that I like, including the slow pace and the visuals, with their minimalistic background and palette of black, white and red. The camera work is superb.
I welcomed the idea of a Love formula, because mathematics is ready to broaden the scope of its models, including venturing into love. Of course, some mathematical models of relationships already exist.

It's great that the mathematician is portrayed against the stereotype: he's neither introverted nor asexual. Unfortunately, the movie plays into other stereotypes of male mathematicians — being creepy and demanding sacrifices from their wives in the name of mathematics.
As I mentioned, I was looking forward to the movie, hoping that it would encourage the imagination of viewers in their interpretations. To my disappointment, every scene in the movie is preceded by text that describes the plot, removing any flexibility of interpretation. Besides that, the emotions portrayed didn't quite match the written plot, in no small part because Ed Frenkel is not a good actor.
The idea of preserving a formula by tattooing it on someone is beyond strange. He could have used a safe-deposit box. Or put the formula in an envelope and given it to the lover to keep, or just encrypted it, etc. With narcissistic lack of consciousness, the Mathematician seems unaware of the implications of his action of imprinting this dangerous secret on Mariko. She can never go swimming, or go to the gym, or be intimate with anyone else. Moreover, if the bad guys discover that Mariko is the Mathematician's lover, her life will be in grave danger. Not to mention that tattooing is painful.
Something that could have been interesting and watchable in a historic movie, in this contemporary movie seems pointlessly cruel, dehumanizing and senseless.
I know for sure that Ed Frenkel is not stupid, so what are his reasons for constructing the plot in this way? Before investigating his reasons, I have a mathematical complaint about the movie. Every mathematician and teacher knows that when asserting a formula you need to indicate its interpretation: what its symbols refer to in the real world. For example, suppose I tell you my own great Formula of Love: Cn = (2n)!/(n+1)!n!. You may recognize Cn as the Catalan numbers, but what does this have to do with Love? To give the formula meaning I need to tell you that Cn is the number of ways you can seat n loving couples at a round table with 2n chairs, so that each couple can join hands (assuming the arms are long enough to reach across the table) without any two pairs of arms crossing. Assigning an interpretation makes the Catalan numbers part of the world's growing body of romantic research.
Writing a formula without mentioning what the variables mean fails to preserve it for the future. Ed Frenkel knows that. Wait a minute. The formula in the movie is actually not the Formula of Love, but a real formula from Ed's paper on instantons. It's right there, formula 5.7 on page 74. Every variable is explained in the paper. Ah-ha! So his movie isn't actually about art, but rather about Ed's formula. Indeed, there is no real Formula of Love. In such situations in other movies, they have simply shown fragments of a formula. However, in Rites of Love and Math, Frenkel's formula — which has nothing to do with Love — is shot in full view, zooming in slowly.
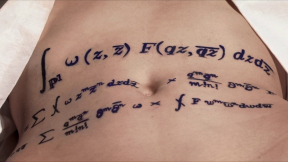
The movie is a commercial. Ed is using our fascination with sex to popularize his formula, and using his formula and his scientific standing to advertise his body.
I was so disappointed that the default interpretation of the movie was imposed on me by those pre-scene texts, that I decided to watch the movie for a second time, trying to ignore the text, hoping to find some new meaning.
If you decide to see the movie, you'll probably come up with your own interpretation of the plot. I actually came up with several. I had a funny one and an allegorical one, but the most interesting task for me was to try create an interpretation matching the emotions portrayed:
Mariko knows that something is wrong in her sex life with the Mathematician. But she still loves him and writes him a love letter. The Mathematician comes to Mariko's place. He is distant and cold. They cuddle. He explains to her that sex doesn't bring him pleasure anymore and that moreover, he can't even perform. He tells her that the only thing that brings him joy is mathematics and suggests that his sexual dysfunction and lack of pleasure will be fixed if they tattoo his favorite formula on her body. She agrees, but first they decide to give sex a last try. They try real hard. But he can't relax and he doesn't enjoy it, so she agrees to the tattoo. He does get excited during the tattooing process itself, but once he finishes his whole formula, he is no longer turned on. Mariko's suffering has been in vain.

Janet Mertz wrote several papers about the gender gap in mathematics. One of her research ideas was to find girls who went to the International Math Olympiad (IMO) and compare their fate to that of their teammates with a similar score. She asked me to find Soviet and Russian IMO girls. All my life I had heard about Lida Goncharova, the first girl on a Soviet team, and the first girl in the world who took a gold medal, but I had never dared to reach out to her. A little push by Janet Mertz was enough for me to find Lida's phone number in Moscow and call her.

Lida got interested in mathematics when she was five years old. Luckily, many of her relatives were mathematicians and she started bugging them for math puzzles.
Her involvement with math was interrupted by the death of her parents — her mother when she was seven, and her father when she was nine. She ended up living with her sister, but felt very lonely.
After several years of personal turmoil, she renewed her pursuit of mathematics. Lida started discussing math with her mother's first husband. She joined a math circle which was run at Moscow State University. When she was 13 she went to a summer camp and found a mentor there to study trigonometry. Eventually she ended up at School Number 425, one of the first schools in Moscow that opened for children gifted in math.
At the end of high school she went to the IMO as part of the Soviet team and won a gold medal there. After that she enrolled in the most prestigious Soviet institute for the study of math — Moscow State University (MSU).
Half of her high school classmates went to MSU, including her high school sweetheart Alexander Geronimus. Lida married Alexander when she was a sophomore and they had their first son in her fourth year of undergraduate school.
Meanwhile, she wasn't doing as well in her studies as she had hoped. Lida was very fast to pick up math ideas during conversations, but she had difficulty reading books. As ideas were becoming more complicated and involved, this became a problem. She started feeling that she was falling behind her friends. When her friends gathered together to discuss mathematics she couldn't understand everything. She wanted to ask questions, but was too shy. Plus, she didn't want to impose on them. She made a decision to be silent. As a result she started ignoring the conversations of others and became discouraged as she fell behind.
She had her second child at the beginning of graduate school, where she studied under the supervision of Dmitry Fuchs. Lida was already losing her self-esteem and so she chose a self-contained problem that didn't require a lot of outside knowledge. The solution involved some combinatorial methods, but Lida didn't quite understand the big picture and the problem's goal.
I contacted Dmitry Fuchs and asked him about Lida's thesis. He told me that Lida's main result is extremely important and widely cited. It is called Goncharova's theorem.
Meanwhile, her husband finished his PhD in math and secured a great job in an academic institution. They had started as peers, but her work was interrupted by having their children. Lida finished her PhD a couple of years after her husband and got a very boring job as an algorithm designer. She even wrote some papers at the job, but she was not much interested. She continued her attempts to do mathematics and continued asking everyone for problems, but it didn't go anywhere. Her friends were not very interested in her calculations and after the birth of her third child she began to lose hope in her research.
When Lida and her husband entered graduate school they became religious. Ten years later, Alexander decided to pursue the Russian Orthodox religion as a career and got a parish 600 km from Moscow. They didn't want to move their children away from Moscow, with its educational and cultural opportunities. So they started living in two places with long commutes. This didn't help her math either.
Eight years after the third son, the fourth son was born. Although Lida sporadically continued her calculations, she still didn't talk about them to anyone.
When the older children went to high school, Lida enjoyed solving their math problems tremendously. In 1990 perestroika started and Lida lost her job. She got an offer to create a private school and teach there. By this time she had had two more children, a son and a daughter. Lida continued working for the private school until her six children grew out of it. Lida enjoyed teaching and inventing methods to teach mathematics. The school ended in 2004. But she continues working with kids sharing with them her joy of mathematics.
Lida believes that she has had an extremely lucky life in many ways. The only exception was her unsuccessful math career. She can't live without math, and will continue working with kids, solving fun problems and doing her private research.
When I first called her and said I wanted to talk about her and math, she told me: —There is nothing to talk about. I stopped doing math after my PhD. Almost.— That —almost— kept me asking questions.

Janet Mertz was considering a serious research project comparing the fates of IMO medal girls with the fates of their teammates, to see whether gender plays a role later. However, due to the language and cultural differences and the fact that most of the girls changed their last name, it was difficult to locate them. So Mertz put this research project on hold.
She had asked me to find and contact the Russian women and I was so fascinated with Lida's story that I decided to write it up in this article. And because the research is on hold, I decided to include the fates of Lida's teammates.
Lida Goncharova got her gold medal in the 1962 IMO with 42 points and was ranked third. The teammate with the closest score was Joseph Bernstein with another gold medal and 46 points. I don't even have to check Wikipedia to tell you about Joseph, as I was once married to him. He used to be a professor at Harvard University and is now a professor at Tel-Aviv University. He is a member of the Israel Academy of Sciences and Humanities and the United States National Academy of Sciences. He achieved a lot and is greatly respected by his peers.
Joseph Bernstein might not be the best person to compare Lida to as he had a perfect score. Some might argue that a perfect score indicates that he might have done better if the problems had been more difficult.
The two Soviet teammates whose scores were the closest to that of Lida, but below her, were Alexey Potepun with 37 points and Grigory Margulis with 36 points.
Alexei Potepun got a PhD in mathematics and is now a professor at Saint-Petersburg University. He has published eleven papers.
Next to Alexey Potepun is Grigory Margulis, who is a professor at Yale and was awarded the Fields Medal and the Wolf Prize. He is a member of the U.S. National Academy of Sciences.
You might notice that the two people who moved to the US are much more famous than those who stayed in Russia. You might say that moving to the US is a better predictor of success than gender. Sure, living in a free country helps, but Margulis got his Fields medal while he was in the USSR. And Bernstein invented his famous D-Modules while in Russia also.
My conversation with Lida was personally inspiring. I loved the tone of her voice when she talked about mathematics. There were many elements that prevented her from having the mathematical career she might have had: the untimely death of her parents, her shyness, raising six children, many years of long commutes. When we look at the achievements of her closest teammates, we can't help but wonder what kind of mathematics we lost.
This conversation was very encouraging for me. I felt there were similarities between Lida and myself in more ways than I expected. What we share most of all is a love for mathematics. I could hear that in her voice.
I gave my students a problem from the 2002 AMC 10-A:
Tina randomly selects two distinct numbers from the set {1, 2, 3, 4, 5}, and Sergio randomly selects a number from the set {1, 2, …, 10}. The probability that Sergio's number is larger than the sum of the two numbers chosen by Tina is: (A) 2/5, (B) 9/20, (C) 1/2, (D) 11/20, (E) 24/25.
Here is a solution that some of my students suggested:
On average Tina gets 6. The probability that Sergio gets more than 6 is 2/5.
This is a flawed solution with the right answer. Time and again I meet a problem at a competition where incorrect reasoning produces the right answer and is much faster, putting students who understand the problem at a disadvantage. This is a design flaw. The designers of multiple-choice problems should anticipate mistaken solutions such as the one above. A good designer would create a problem such that a mistaken solution leads to a wrong answer — one which has been included in the list of choices. Thus, a wrong solution would be punished rather than rewarded.
Readers: here are three challenges. First, to ponder what is the right solution. Second, to change parameters slightly so that the solution above doesn't work. And lastly, the most interesting challenge is to explain why the solution above yielded the correct result.
This is a version of the standard charades game that my son, Sergei Bernstein, invented.
Unlike in regular charades, the person who acts out the phrase doesn't know what the phrase is and has to guess it. The viewers on the other hand, know the phrase but they are not allowed to talk.
So the actor is blindfolded and the viewers are not just watching; they are actively moving the actor and his/her body parts around to communicate the phrase. For example, if the actor is on the right track, since the viewers can't say, "Yes, good!", they might communicate it by nodding the actor's head.
Sounds like fun, especially for people who enjoy touching and being touched.
Once again I am one of the organizers of the Women and Math Program at the Institute for Advanced Study in Princeton, May 16-27, 2011. It will be devoted to an exciting modern subject: Sparsity and Computation.
In case you are wondering about the meaning of the picture on the program's poster (which I reproduce below), let us explain.

The left image is the original picture of Fuld Hall, the main building on the IAS campus. The middle image is a corrupted version, in which you barely see anything. The right image is a striking example of how much of the image can be reconstructed from the corrupted image using clever algorithms.
Female undergraduates, graduates and postdocs are welcome to apply to the program. You will learn exactly how the corrupted image was recovered and much more. The application deadline is February 20, 2011.
Eugene Brevdo generated the pictures for our poster and agreed to write a piece for my blog explaining how it works. I am glad that he draws parallels to food, as the IAS cafeteria is one of the best around.
The three images you are looking at are composed of pixels. Each pixel is represented by three integers corresponding to red, green, and blue. The values of each integer range between 0 and 255.
The image of Fuld hall has been corrupted: some pixels have been replaced with all 0s, and are therefore black; this means the pixel was not "observed". In this corrupted version, 85% of the pixel values were not observed. Other pixels have been modified to various degrees by stationary Gaussian noise (i.e. independent random noise). For the 15% observed pixel values, the PSNR is 6.5 db. As you can see, this is a badly corrupted image!
The really interesting image is the one on the right. It is a "denoised" and "inpainted" version of the center image. That means the pixels that were missing were filled in and the observed pixel integer values were re-estimated. The algorithm that performed this task, with the longwinded name "Nonparametric Bayesian Dictionary Learning," had no prior knowledge about what "images should look like". In that sense, it's similar to popular wavelet-based denoising techniques: it does not need a prior database of images to correct a new one. It "learns" what parts of the image should look like from the original image, and fills them in.
Here's a rough sketch of how it works. The idea is to use a new technique in probability theory — the idea that a a patch, e.g. a contiguous subset of pixels, of an image is composed of a sparse set of basic texture atoms (from the "Dictionary"). Unfortunately for us, the number of atoms and the atoms themselves are unknowns and need to be estimated (the "Nonparametric Learning" part). In a way, the main idea here is very similar to Wavelet-based estimation, because while Wavelets form a fixed dictionary, a patch from most natural images is composed of only a few Wavelet atoms; and Wavelet denoising is based on this idea.
We make two assumptions that allow us to simplify and solve this problem, which is unwieldy-sounding and vague when the texture atoms have to be estimated. First, there may be many atoms, but a single patch is a combination of only a sparse subset of them. Second, because each atom appears in part in many patches, even if we observe some noisily, once we know which atoms appear in which patches, we can invert and average together all of the patches associated with an atom to estimate it.
To explain and programmatically implement the full algorithm that solves this problem, probability theorists like to explain things in terms of going to a buffet. Here's a very rough idea. There's a buffet with a (possibly infinite) number of dishes. Each dish represents a texture atom. An image patch will come up to the buffet and, starting from the first dish, begins to flip a biased coin. If the coin lands on heads, the patch takes a random amount of food from the dish in front of it (the atom-patch weight), and then walks to the next dish. If the coin lands on tails, the patch skips that dish and instead just walks to the next. There it flips its coin with a different bias and repeats the process. The coins are biased so the patch only eats a few dishes (there are so many!). When all is said and done, however, the patch has eaten a random amount from a few dishes. Rephrased: the image patch is made from a weighted linear combination of basic atoms.
At the end of the day, all the patches eat their own home-cooked dessert that didn't come from the buffet (noise), and some pass out from eating too much (missing pixels).
If we know how much of each dish (texture atom) each of the patches ate and the biases of the coins, we can estimate the dishes themselves — because we can see the noisy patches. Vice versa, if we know what the dishes (textures) are, and what the patches look like, we can estimate the biases of the coins and how much of a dish each patch ate.
At first we take completely random guesses about what the dishes look like and what the coins are, as well as how much each patch ate. But soon we start alternating guesses between what the dishes are, the coin biases, and the amounts that each patch ate. And each time we only update our estimate of one of these unknowns, on the assumption that our previous estimates for the others is the truth. This is called Gibbs sampling. By iterating our estimates, we can build up a pretty good estimate of all of the unknowns: the texture atoms, coin biases, and the atom-patch weights.
The image on the right is our best final guess, after iterating this game, as to what the patches look like after eating their dishes, but before eating dessert and/or passing out.
I've heard many fun problems in which blindfolded parachutists are dropped somewhere and they need to meet up once they're on the ground. They can't shout or purposefully leave traces behind. They will recognize each other as soon as they bump into each other. Their goal is to get to the same assembly point. They can design their strategy in advance.
Here is the first problem in a series that gets increasingly difficult:
Two parachutists are dropped at different locations on a straight line at the same time. Both have an excellent sense of direction and a good geographical memory, so both know where they are at any moment with respect to their starting point on the line. What's their strategy?
The strategy is that the first person stands still and the second one goes forward and back repeatedly, increasing the distance of each leg until they collide.
In the next variation, both are required to execute the same program, that is, if one stands still, then both stand still. To compensate for this increased difficulty, they are allowed to leave their parachutes anywhere. And both of them will recognize the other's parachute if they bump into it.
In the third variation, the set-up is similar to the previous problem, but they are not allowed to change the direction of their movement. To their advantage, they know which way East is.
I recently heard a 2-D version from my son Sergei in which the parachutists are ghosts. That means that when they bump into each other they go through each other without even recognizing the fact that they met:
Several blindfolded men are sleeping at different locations on a plane. Each wakes up, not necessarily at the same time. At the moment of waking up, each of them receives the locations of all the others in relation to himself at that moment. They are not allowed to interact, nor will they receive any further information as time passes. They need to get together in one place. How can they do that, if they are allowed to decide on their strategy in advance?
They do not know where North is. So they can't go to the person at the most Northern point. Also they do not know how locations correspond to people, so they can't all go to where, say, Peter is. Let us consider the case of two men. Suppose they decide to go to the middle of the segment of two locations they receive when they awake. But they get different locations because they wake up at different times. Suppose the first person wakes up and goes to the middle. The fact that he walks while the other is sleeping, means that he changes the middle. So when the second person wakes up, his calculated middle is different from the one calculated by the first person. Consequently, they will never manage to meet. Hence, the solution should be different.
Actually Sergei gave me a more difficult problem:
Not only do they need to meet, but they need to stay together for a predefined finite time period.
Here is as bonus problem.
If there are three parachutists, it is possible to end up in a meeting place and stay there indefinitely. For four people it is often possible too.
Darth Maul killed Qui-Gon Jinn. Obi-Wan Kenobi killed Darth Maul. Palpatine killed Mace Windu. Darth Vader killed Obi-Wan Kenobi and Palpatine. I am mentally drawing the kill graph of Star Wars, where people are vertices and kills are edges. The graph is not very interesting. In movies where no one gets resurrected, the kill graph is a forest.
I'm interested in studying social networks in the movies and how they differ from social networks in real life. As we saw, the kill graph is not very exciting mathematically.
Now let's try the acquaintance graph, where edges mark two people who know each other. Unfortunately, in the movies there are often many nameless people and we learn very little about their acquaintances. On the other hand, all the "nameful" people usually know each other, thus their acquaintance graph is a complete graph. The richest acquaintance graphs would be for epic movies like Star Wars, in which the events span two generations and many planets. As a result, there are characters who never meet each other. For example, Leia, Luke and Han from the original trilogy never meet people who died in the prequel, such as Anakin's mother and Count Dooku.
But I think that the most intriguing type of filmic social network is the fight graph, where edges represent characters who fight each other. Usually such graphs are bipartite, reflecting the division between bad guys and good guys. When an epic film is more complex and has traitors, the fight graph is no longer bipartite. Consider Darth Vader who fought and killed a lot of good guys including Obi-Wan Kenobi as well as many bad guys including Count Dooku and the Emperor.
I would like to immortalize Darth Vader in mathematics. He did restore the balance to the Force. If there is a graph which is not bipartite and can become bipartite by removing one highly connected node, I would like to name such a node Darth Vader.
Dear Nita Palmira,
I do not recall your name and I'm not sure where you got my email address from, but I really appreciate you contacting me. I am excited by your Two-Procedures-For-The-Price-Of-One offer. I am really looking forward to my enlarged penis and my DDD breasts.
Meanwhile, I can give you a unique group discount on IQ tests. I can test the IQ of all your company employees for the price of one test. Moreover, you do not need to waste even a minute. Actually, no one even needs to answer any questions. You can send me your $500 check to the address below and I will promptly send you the IQ report, the accuracy of which I can guarantee.
Sincerely yours.
I am coaching my AMSA students for math competitions. Recently, I gave them the following problem from the 1964 MAML:
The difference of the squares of two odd numbers is always divisible by:
A) 3, B) 5, C) 6, D) 7, E) 8?
The fastest way to solve this problem is to check an example. If we choose 1 and 3 as two odd numbers, we see that the difference of their squares is 8, so the answer must be E. Unfortunately this solution doesn't provide any useful insight; it is just a trivial calculation.
If we remove the choices, the problem immediately becomes more interesting. We can again plug in numbers 1 and 3 to see that the answer must be a factor of 8. But to really solve the problem, we need to do some reasoning. Suppose 2k + 1 is an odd integer. Its square can be written in the form 4n(n+1) + 1, from which you can see that every odd square has remainder 1 when divided by 8. A solution like this is a more profitable investment of your time. You understand what is going on. You master a method for solving many problems of this type. As a bonus, if students remember the conclusion, they can solve the competition problem above instantaneously.
This is why when I am teaching I often remove multiple choices from problems. To solve them, rough estimates and plugging numbers are not enough. To solve the problems the students really need to understand them. Frankly, some of the problems remain boring even if we remove the multiple choices, like this one from the 2009 AMC 10.
One can holds 12 ounces of soda. What is the minimum number of cans needed to provide a gallon (128 ounces) of soda?
It's a shame that many math competitions do not reward deep analysis and big-picture understanding. They emphasize speed and accuracy. In such cases, plugging in numbers and rough estimates are useful skills, as I pointed out in my essay Solving Problems with Choices.
In addition, smart guessing can boost the score, but I already wrote about that, too, in How to Boost Your Guessing Accuracy During Tests and To Guess or Not to Guess?, as well as Metasolving AMC 8.
As the AMC 10 fast approaches, I am bracing myself for the necessity to include multiple choices once again, thereby training my students in mindless arithmetic.

Many people ask me when is a good time to teach kids math. In my experience, it can never be too early. You just need to keep some order. Multiplication should be taught after addition, and negative numbers after subtraction. Kids should remember multiplication by heart at the age of seven. They can understand negative numbers as early as four.
In the picture I am explaining Platonic solids to four-month-old Eli, the son of my friends. His homework is to chew on a dodecahedron.
Suppose Romeo is encouraged by love and attention. If Juliet likes him, his feelings for Juliet grow and flourish. If she doesn't like him, he loses his interest in her.
Juliet, on the other hand, is the opposite. If Romeo doesn't like her, she needs to win him over and her attraction for him grows. If he likes her, she feels that her task is accomplished and she loses her interest in him. Juliet likes the challenge more than the relationship.

Steven Strogatz used differential equations to model the dynamics of the relationship between Romeo and Juliet. This is a new and fascinating area of applied mathematical research; you can read more about the roller-coaster relationship between Romeo and Juliet in Steven Strogatz's Nonlinear Dynamics and Chaos: With Applications to Physics, Biology, Chemistry, and Engineering.
Mathematicians like symmetry: in math literature they switch the roles between Romeo and Juliet randomly. So in some papers they give Romeo the role of preferring a challenge over love and in some papers they give that role to Juliet.
When I teach this subject of love, Alexander Pushkin's famous quote always pops into my mind. The quote comes from the first lines of Chapter Four of Eugene Onegin, and in Russian it is:
Чем меньше женщину мы любим,
Тем легче нравимся мы ей…
I didn't like the English translations that I found, so I asked my son Alexey to provide a more literal translation:
The less we love a woman, the more she likes us in return…
I blame Pushkin for my tendency to always pick Juliet as the character who thrives on the challenge, even though men are often assumed to be the chasers. I'd like to ask my readers to comment on these roles: Do you think both genders play these roles equally? If not, then who is more prone to be into the chase?
Let's return to mathematical models. In the original model, the reactions of Romeo and Juliet are a linear function of feelings towards them. I would like to suggest two other roles, in which people react to the absolute value of feelings towards them. They do not care if it is love or hate: they care about intensity.
First, there is the person, like my friend Connie, who feeds on the emotions of other people. She's turned on by guys who love her as well as by guys who hate her. If they're indifferent, she's turned off.
Second, there is the opposite type, like my colleagues George, Joseph, David and many others. They hate emotion and prefer not to be involved. They lose all interest in people who feel strongly about them and they like people who are distant. I know the name for this role: it's a mathematician!

My friend Olga Amosova worked as a molecular biologist at Princeton University. Last time I visited her, we talked about her research.
She told me that she and her group designed a repair for a DNA mutation that is highly localized. "What's the point," I asked her, "of repairing DNA mutation in one cell?"
I was amazed to learn that not only is there a practical use to her research, but that there is something urgent that I myself must do.
There are many diseases that are caused by localized (so called "point") mutations. The most famous one is Sickle-cell disease. In Sickle-cell disease, defective hemoglobin causes erythrocytes to adopt a sickle shape that makes it difficult to pass through blood vessels. It is a very painful and debilitating disease. However, it turns out that the results of the research of Olga and her group could make the lives of people with such mutations much easier.
Stem cells have two amazing abilities. They grow fast and they can be turned into any type of cells in the human body. If the mutation is repaired in just one stem-cell, it can be selected and turned into a blood progenitor cell. These progenitor cells produce erythrocytes that actually transport oxygen. If these repaired cells are added to the patient's blood, they would produce good hemoglobin for half a year. This would improve the patient's quality of life tremendously.
So what do the rest of us learn from Olga's research? That we must save all left-over stem-cells that are produced in childbirth, like the umbilical cord and the placenta. It's not only Sickle-cell, but many other diseases that could benefit from using stem-cells. Research is moving so fast that these frozen stem-cells might become relevant in surprising ways — not only for the child, but also for relatives of the child — like you yourself!
So what's the urgent thing I must do? My son recently got married, so I must finish this post and send it to my son in case they get pregnant.
Mikhail Zhvanetsky is the most prolific and famous Russian humorist. Here are my own translations of some of his best lines.

I love the TV series of Angel and of Buffy the Vampire Slayer. I enjoy the excitement of saving the world every 42 minutes. But as a scientist I keep asking myself a lot of questions.
Where do vampires take their energy from? Usually oxygen is the fuel for the muscles of living organisms, but vampires do not breathe. Vampires are not living organisms, and yet they have to get their energy from somewhere.
When you kill a vampire, it turns to dust. If organisms are 60% water, then a 200-pound vampire should generate 80 pounds of dust. So why, in the series, do you get just a little puff of dust whenever someone plunges a stake into a vampire? Plus 120 pounds of water apparently evaporates instantly during staking. Can someone who is less lazy than me please calculate the energy needed to evaporate 120 pounds of water in one second? Because my first reaction is that you would need an explosion, not just one stab with Buffy's stake.
All these unscientific elements do not actually bother me that much. What does bother me are inconsistencies in logic. For example, at the end of Season One of Buffy, Angel refuses to give Buffy CPR, claiming that as a vampire he can't breathe. But then how can Spike and other vampires smoke? If they can smoke that means they are capable of inhaling and exhaling. Not to mention that these vampires talk: wouldn't they need an airflow through their throats to produce sounds?
It would make more sense for the show to state that vampires do not need to breathe, but are nonetheless capable of inhaling and exhaling. So Angel should have given Buffy CPR. It would have created a great plot twist: Angel saves Buffy at the end of Season One, only for her to send him to the hell dimension at the end of Season Two.
Back to breathing. I remember a scene in "Bring On the Night" in which Spike was tortured by Turok-Han holding his head in water. But if Spike can't breathe, why is this torture?
Another thing that bothers me in the series is not related to what happens but to what doesn't happen. For example, vampires do not have reflections. So I don't understand why every vampire-aware person didn't install a mirror on the front door of their house to check for reflections before inviting anyone in.
Also, it looks like producers do not care about backwards compatibility. Later in the series we get to know that vampires are cold. Watch the first season of Buffy with that knowledge. In the very first episode, Darla is holding hands with her victim, but he doesn't notice that she is cold. Later Buffy kisses Angel, before she knows that he is a vampire, and she doesn't notice that he's cold either. Unfortunately, the series also isn't forward compatible. In the second season of Angel in the episode "Disharmony", when we already know that vampires are cold, Harmony is trying to reconnect with Cordelia. They hug and touch each other. Such an experienced demon fighter as Cordelia should have noticed that Harmony is cold and, therefore, dead.
Finally, let's look at Spike in the last season of Angel. Spike is non-corporeal for a part of the season; we see him going through walls and standing in the middle of a desk. Yet, one time we see him sitting on a couch talking to Angel. In addition, he can take the stairs. He can go through the elevator wall to ride in an elevator instead of falling down through its floor. And what about floors? Why isn't he falling through floors? Some friends of mine said that we can assume that floors are made from stronger materials. But, if there is a material that can prevent Spike from penetrating it, they ought to use this material to make a weapon for him.
I've never been involved in making a show, but these producers clearly need help. Perhaps they should hire a mathematician like me with an eye for detail to prevent so many goofs.
The jokes are a rough translation from a Russian collection, except the last one I invented myself.
* * *
— Moishe, do you know how many cuckolds are there in Odessa not counting you?
— What? What do you mean by saying "not counting you"?
— Sorry. Okay then, how many counting you?
* * *
At a very prestigious Russian nursery school a teacher talks to a four-year-old applicant.
"Mike, can you count for me?"
Mike counts very fast and with a lot of enthusiasm, "Fifty-nine, fifty-eight, fifty-seven…"
"Super," says the teacher, "But how did you learn to count backwards?"
Mike replies proudly, "I can heat my own lunch — in the microwave."
* * *
The curl of the curl equals the gradient of the divergence minus the Laplacian. Why do I remember this shit that I never need, but can't remember where I put my keys yesterday?
* * *
In a bike store:
Customer: "Can you show me your finest helmet? I've already spent $200,000 on my head, so I don't want to take any risks."
Clerk, sympathetically: "You had a head trauma?"
Customer: "No, I went to college."
* * *
A topologist walks into a cafe:
— Can I have a doughnut of coffee, please.
In my old essay I presented the following coin problem.
We have N coins that look identical, but we know that exactly one of them is fake. The genuine coins all weigh the same. The fake coin is either lighter or heavier than a real coin. We also have a balance scale. Unlike in classical math problems where you need to find the fake coin, in this problem your task is to figure out whether the fake coin is heavier or lighter than a real coin. Your challenge is that you are only permitted to use the scale twice. Find all numbers N for which this can be done.
Here is my solution to this problem. Let us start with small values of N. For one coin you can't do anything. For two coins there isn't much you can do either. I will leave it to the readers to solve this for three coins, while I move on to four coins.
Let us compare two coins against the other two. The weighing has to unbalance. Then put aside the two coins from the right pan and compare one coin from the left pan with the other coin from the left pan. If they balance, then the right pan in the first weighing contained the fake coin. If they are unbalanced then the left pan in the first weighing contained the fake coin. Knowing where the fake coin was in the first weighing gives us the answer.
It is often very useful to go through the easy cases. For this problem we can scale the solution for three and four coins to get a solution for any number of coins that is divisible by three and four by just grouping coins accordingly. Thus we have solutions for 3k and 4k coins.
For any number of coins we can try to merge the solutions above. Divide all coins into three piles of size a, a and b, where a ≤ b ≤ 2a. In the first weighing compare the first two piles. If they balance, then the fake coin must be among the b remaining coins. Now pick any b coins from both pans in the first weighing and compare them to the remaining b coins. If the first weighing is unbalanced, then the remaining coins have to be real. For the second weighing we can pick a coins from the remaining pile and compare them to one of the pans in the first weighing.
The solution I just described doesn't cover the case of N = 5. I leave it to my readers to explain why and to solve the problem for N = 5.
Among ten given coins, some may be real and some may be fake. All real coins weigh the same. All fake coins weigh the same, but have a different weight than real coins. Can you prove or disprove that all ten coins weigh the same in three weighings on a balance scale?
When I first received this puzzle from Ken Fan I thought that he mistyped the number of coins. The solution for eight coins was so easy and natural that I thought that it should be eight — not ten. It appears that I was not the only one who thought so. I heard about a published paper with the conjecture that the best you can do is to prove uniformity for 2n coins in n weighings.
I will leave it to the readers to find a solution for eight coins, as well as for any number of coins less than eight. I'll use my time here to explain the solution for ten coins that my son Sergei Bernstein suggested.
First, in every weighing we need to put the same number of coins in both pans. If the pans are unbalanced, the coins are not uniform; that is, some of them are real and some of them are fake. For this discussion, I will assume that all the weighings are balanced. Let's number all coins from one to ten.
Consider two sets. The first set contains only the first coin and the second set contains the second and the third coins. Suppose the number of fake coins in the first set is a and a could be zero or one. The number of fake coins in the second set is b where b is zero, one or two. In the first weighing compare the first three coins against coins numbered 4, 5, and 6. As they balance the set of coins 4, 5, and 6 has to have exactly a + b fake coins.
In the second weighing compare the remaining four coins 7, 8, 9, and 10 against coins 1, 4, 5, and 6. As the scale balances we have to conclude that the number of fake coins among the coins 7, 8, 9, and 10 is 2a + b.
For the last weighing we compare coins 1, 7, 8, 9, and 10 against 2, 3, 4, 5, and 6. The balance brings us to the equation 3a + b = a + 2b, which means that 2a = b. This in turn means that either a = b = 0 and all the coins are real, or that a = 1, and b = 2 and all the coins are fake.
Now that you've solved the problem for eight and less coins and that I've just described a solution for ten coins, can we solve this problem for nine coins? Here is my solution for nine coins. This solution includes ideas of how to use a solution you already know to build a solution for a smaller number of coins.
Take the solution for ten coins and find two coins that are never on the same pan. For example coins 2 and 10. Now everywhere where we need 10, use 2. If we need both of them on different pans, then do not use them at all. The solution becomes:
The first weighing is the same as before with the same conclusion. The set containing the coin 1 has a fake coins, the set containing the coins 2 and 3 has b fake coins and the set containing coins 4, 5, and 6 has to have exactly a + b fake coins.
In the second weighing compare the four coins 7, 8, 9, and 2 against 1, 4, 5, and 6. As the scale balances we have to conclude that the number of fake coins among 7, 8, 9, and 2 is 2a + b.
For the last weighing we compare coins 1, 7, 8, and 9 against 3, 4, 5, and 6. If we virtually add the coin number 2 to both pans, the balance brings us to the equation 3a + b = a + 2b, which means that 2a = b. Which in turn means, similar to above, that either all the coins are real or all of them are fake.
It is known (see Kozlov and Vu, Coins and Cones) that you can solve the same problem for 30 coins in four weighings. I've never seen an elementary solution. Can you provide one?
I am starting yet another part-time job as the Head Mentor at PRIMES, a new MIT research program for high schoolers. I am very excited about this program, for it will be valuable not only to kids who want to become researchers, but also to kids who just want to see what research is like. Kids who want to learn to think in a new way will also find it highly useful.
PRIMES is in many ways similar to RSI, which it augments and complements. There are also a lot of differences. Keep in mind that I am only comparing PRIMES to the math part of RSI, with which I was working as a coordinator for two years. I do not know how RSI handles other sciences.
Different time scale. RSI lasts six weeks; PRIMES will take about a year. I already wrote about some peoples' skepticism towards RSI in my piece called "Fast Food Research?." PRIMES creates a more natural pace for research.
Choices. Because of the time schedule at RSI, students get their project as soon as they start. Students who realize by the end of the second week that they do not like their project are at a disadvantage: if they do not change their project, they're stuck with something that does not inspire them or is too difficult, and if they do change their project, they won't have enough time to do a great job. At PRIMES students will have time to talk to the mentors before starting their project, so that they can participate in choosing their project. Depending on how it goes later, they'll have time to try several different directions. I believe that the best research comes from the heart: students who have the time and opportunity to shape their choices will be more invested in their project.
Application process. At RSI, The Center for Excellence in Education reviews the applications. Even though they usually do a superb job at sending us great students, I believe it would be an advantage if mentors were able to influence the review process, for they might find even better matches to their projects. At PRIMES, the mentors will have this opportunity to review the applications.
Geography. RSI accepts students from all over the US and from some other countries. PRIMES can only accept local students — those who live close enough to visit MIT once a week for four months. Because of this restriction, PRIMES is recruiting from a smaller pool of students than RSI. But for local students it means that it will be easier to get accepted to PRIMES than to RSI.
Coaching. At RSI, students get a lot of coaching. I think that every student is in close contact with four adults. Two of them are from the math department — mentor and coordinator (that's me!) — and two tutors from CEE. PRIMES will have less coaching. A student will have a mentor and me, the head mentor. In addition, mentors might arrange for students to talk to the professors who originated their projects.
Immersion. RSI students are physically present. They are housed at MIT with the expectation that they completely devote their time to their research. Students at PRIMES will be integrating their research into the rest of their lives and their commitments. That will require good organizational skills and a lot of self-discipline. RSI students have discipline imposed on them by their situation — which may be an advantage to them.
Olympiads. While they are at RSI, students can't go to IMO or other summer activities. This is why many strong Olympiad students choose not to go to RSI, or they turn down an RSI acceptance if in the meantime they have gotten on to an Olympic team. At PRIMES you can do both. It is possible to go to an Olympiad, in addition to writing a paper.
Grade. RSI students have to be juniors. There are no grade limitations for PRIMES. Thus, it is possible to go to PRIMES in one's senior year. In this case, it may be too late to use PRIMES on college applications, but it is perfectly fine for the sake of research itself. Or it might be possible to go to PRIMES as a sophomore, and then apply for RSI the next year. This will strengthen the student's application for RSI.
RSI is well-established and has proven itself. PRIMES is new and hopefully will offer young mathematicians additional opportunities to try research.
I think that the American system of education creates a lot of pressure for teachers to drill their students for standardized tests and multiple choice questions. This blocks creative thinking. Every program like PRIMES is very good for unleashing students' creativity and contributing to the development of the future thinkers of American society.
Silvio Micali taught me cryptography. To explain one-way functions, he gave the following example of encryption. Alice and Bob procure the same edition of the white pages book for a particular town, say Cambridge. For each letter Alice wants to encrypt, she finds a person in the book whose last name starts with this letter and uses his/her phone number as the encryption of that letter.
To decrypt the message Bob has to read through the whole book to find all the numbers. The decryption will take a lot more time than the encryption. If the book increases in size the time it takes Alice to do the encryption almost doesn't increase, but the decryption process becomes more and more draining.
This example is very good for teaching one-way functions to non-mathematicians. Unfortunately, the technology changes and the example that Micali taught me fifteen years ago isn't so cute anymore. Indeed you can do a reverse look-up online of every phone number in the white pages.
I still use this example, with an assumption that there is no reverse look-up. I recently taught it to my AMSA students. And one of my 8th graders said, "If I were Bob, I would just call all the phone numbers and ask their last names."
In the fifteen years since I've been using this example, this idea never occurred to me. I am very shy so it would never enter my mind to call a stranger and ask for their last name. My student made me realize that my own personality affected my mathematical inventiveness.
Since modern technology is murdering my 15-year-old example, I would like to ask my readers to suggest other simple examples of one-way functions or ways to resurrect the white pages example.
I received a message at the beginning of October: "This month has 5 Fridays, 5 Saturdays and 5 Sundays; this only happens every 823 years."
Wait a minute. The Gregorian calendar cycles every 400 years. Where is the figure of 823 coming from?
Wait another minute. Within a century the calendar repeats itself every 28 years. So we are guaranteed that October 2038 will be the same as October 2010.
Wait one more minute. To have a month with five Fridays, Saturdays and Sundays, we need a month that has 31 days and starts on a Friday. There are seven months a year with 31 days, so on average we would expect to have such a month once a year.
If you study the calendar you can see that the seven long months start on six different days. This means that two of the months start on the same day and one of the days is skipped altogether. We see this in both leap years and non-leap years.
Ironically, 2010 is the year with two long months starting on Friday — October and January. Despite the claims of the email about this only happening every 823 years, in fact the same phenomenon occurred twice this year. The next time this will happen is in July 2011.
For those people who get all excited when a month has five Fridays, five Saturdays and five Sundays, I have good news for you. The month following each of these months has to start on Monday. And unless it is a February of a non-leap year, it will have five Mondays.
I asked my son Alexey Radul what exactly he is doing for his postdoc at the Hamilton Institute in Ireland. Here is his reply:
The short, jargon-loaded version: We are building an optimizing compiler for a programming language with first-class automatic differentiation, and exploring mathematical foundations, connections, applications, etc.
Interpretation of jargon:
Automatic differentiation is a technique for turning a program that computes a function into a program that computes that function together with its derivative; with a constant factor overhead. This is better than the usual symbolic differentiation that, say, Mathematica does because there is no intermediate-expression bulge. For example, if your function is a large product
Product f1(x) f2(x) ... fn(x),
the symbolic derivative has size n2
Sum (Product f1'(x) f2(x) ... fn(x)) (Product f1(x) f2'(x) ... fn(x)) ... (Product f1(x) f2(x) ... fn'(x))
automatic differentiation avoids that cost. Automatic (as opposed to symbolic) differentiation also extends to conditionals, data structures, higher-order functions, and all the other wonderful things that distinguish a computer program from a mathematical expression.
First-class means that the differentiation operations are normal citizens of the programming language. This is not the case with commonly used automatic differentiation systems, which are all preprocessors that rewrite C or Fortran source code. In particular, we want to be able to differentiate any function written in the language, even if it is a derivative of something, or contains a derivative of something, etc. The automatic differentiation technique works but becomes more complicated in the presence of higher order, multivariate, or nested derivatives.
We are building an optimizing compiler because the techniques necessary to get good performance and correct results with completely general automatic differentiation are exactly the techniques used to produce aggressive optimizing compilers for functional languages, so we might as well go all the way.
It appears that the AD trick (or at least half of it) is just an implementation of synthetic differential geometry in the computer. This leads one to hope that a good mathematical foundation can be found that dictates the behavior of the system in all the interesting special cases; there is lots of math to be thought about in the vicinity of this stuff.
Applications are also plentiful. Any time you want to optimize anything with respect to real parameters, gradients help. Any time you are dealing with curves, slopes help. Computer graphics, computer vision, physics simulations, economic and financial models, probabilities — there's so much stuff to apply a high quality such system to that we don't know where to begin.
I usually give a lot of lectures and I never used to announce them in my blog. This time I will give a very accessible lecture at the MIT "Women in Mathematics" series. It will be on Wednesday October 6th at 5:30-6:30 PM in room 2-135. If you are in Boston, feel free to join. Here is the abstract.
I will discuss several coin-weighing puzzles and related research. Here are two examples of such puzzles:
1. Among 10 given coins, some may be real and some may be fake. All real coins weigh the same. All fake coins weigh the same, but have a different weight than real coins. Can you prove or disprove that all ten coins weigh the same in three weighings on a balance scale?
2. Among 100 given coins, four are fake. All real coins weigh the same. All fake coins weigh the same, but they are lighter than real coins. Can you find at least one real coin in two weighings on a balance scale?
You are not expected to come to my talk with the solutions to the above puzzles, but you are expected to know how to find the only fake coin among many real coins in the minimum number of weighings.
In 2009 I was working at MIT coordinating math research for Research Science Institute for high school students. One of our students Jacob Hurwitz got a project on decycling graphs.
"Decycling" means removing vertices of a graph, so that the resulting graph doesn't have cycles. The decycling number of a graph is the smallest number of vertices you need to remove.
Decycling is equivalent to finding induced forests in a graph. The set of vertices of the largest induced forest is a complement to the smallest set of vertices you need to remove for decycling.
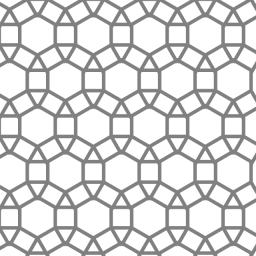
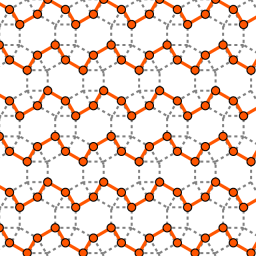
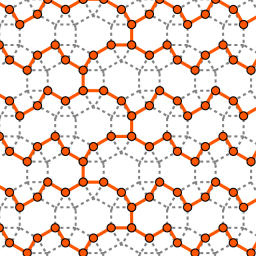
Among other things, Jacob found induced trees and forests of the highest densities on graphs of all semi-regular tessellations. On the pictures he provided for this essay, you can see an example of a tessellation, a corresponding densest forest, and a corresponding densest tree. The density of the forest and the tree is 2/3, meaning that 1/3 of the vertices are removed.
To motivate RSI students I tried to come up with practical uses for their projects. When I was talking to Jacob about decycling, the only thing I could think of was terrorists. When terrorists create their cells, they need to limit connections among themselves, in order to limit the damage to everyone else in the cell if one of them gets busted.
That means the graph of connections of a terrorist cell is a tree. Suppose there is a group of people that we suspect, and we know the graph of their contacts, then the decycling number of the graph is the number of people that are guaranteed to be innocent.
Have you noticed how Facebook and LinkedIn are reasonably good at suggesting people you might know? The algorithm they use to analyze the data is fairly effective in revealing potential connections. Recently, someone was able to download all of the Facebook data, which means that any government agency ought to be able to do the same thing. They could analyze such data to discover implicit connections. As a byproduct of looking for terrorists, they would also discover all of our grudges.
Oh dear. What are they going to think when they find out I'm not connected to my exes?
In the name of privacy, I have changed the names of the men I did not marry. But there is no point in changing the names of my ex-husbands, as my readers probably know their names anyway.
I received my first marriage proposal when I was 16. As a person who was unable to say "no" to anything, I accepted it. Luckily, we were not allowed to get married until I was 18, the legal marriage age in the USSR, and by that time we broke up.
To my next proposal, from Sasha, I still couldn't say "no", and ended up marrying him. The fact that I was hoping to divorce him before I got married at 19 shows that I should have devoted more effort in learning to say "no". I decided to divorce him within the first year.
My next proposal came from Andrey, I said yes, with every intention of living with Andrey forever. We married when I was 22 and he divorced me when I was 29.
After I recovered from my second divorce, I had a fling with an old friend, Sam, who was visiting Moscow on his way to immigrate to Israel.
Sam proposed to me in a letter that was sent from the train he took from the USSR to Israel. At that point I realized I had a problem with saying "no". The idea of marrying Sam seemed premature and very risky. I didn't want to say yes. I should have said no, but Sam didn't have a return address, so I didn't say anything.
That same year I received a phone call from Joseph. Joseph was an old friend who lived in the US, and I hadn't seen or heard from him for ten years. He invited me to visit him in the US and then proposed to me the day after my arrival. The idea of marrying Joseph seemed premature and very risky, but in my heart it felt absolutely right. I said yes, and I wanted to say yes.
I was very glad that I hadn't promised anything to Sam. But I felt uncomfortable. So even before I called my mother to notify her of my marriage plans, I located Sam in Israel and called him to tell him that I had accepted a marriage proposal from Joseph. I needed to consent to marry someone else as a way of saying "no" to Sam.
After I married Joseph, I came back to Russia to do all the paperwork and pick up my son, Alexey for our move to the US. There I met Victor. I wasn't flirting with Victor and was completely disinterested. So his proposal came as a total surprise. That was the time I realized that I had a monumental problem with saying "no". I had to say "no" to Victor, but I couldn't force myself to pronounce the word. Here is our dialogue as I remember it:
My sincere attempt at saying "no" didn't work. I moved to the US to live with Joseph and I soon got pregnant. Victor was the first person on my list to notify — another rather roundabout way to reject a proposal.
The marriage lasted eight years. Sometime after I divorced Joseph, I met Evan who invited me on a couple of dates. I wasn't sure I wanted to get involved with him. But he proposed and got my attention. I was single and available, though I had my doubts about him.
Evan mentioned that he had royal blood. So I decided to act like a princess. I gave him a puzzle:
I have two coins that together make 15 cents. One of them is not a nickel. What are my coins?
He didn't solve it. In and of itself, that wouldn't be a reason to reject a guy. But Evan didn't even understand my explanation, despite the fact that he was a systems administrator. A systems administrator who doesn't get logic is a definite turn-off.
So I said "no"! That was my first "no" and I have mathematics to thank.

When the Women and Math program at IAS was coming to an end, Ingrid Daubechies invited me to a picnic at her place for PACM (The Program in Applied and Computational Mathematics at Princeton University). I accepted with great enthusiasm for three reasons: I was awfully tired and needed a rest; PACM was my former workplace, so I was hoping to meet old acquaintances; and most of all, I loved the chance to hang out with Ingrid.
Ingrid is a great cook, so she prepared some amazing deserts for the picnic. While I was helping myself to a second serving of her superb lemon mousse, a man asked me if I was Ingrid's sister. Ingrid overheard this and laughingly told him that we are soul-sisters.
I admire Ingrid, so at first I took this as a compliment and felt all warm and fuzzy. But when my critical reasoning returned, I had to ask myself: Why would someone think I am Ingrid's sister with my Eastern European round face, my Russian name and my Russian accent?
I started talking to the man. He asked me what I do. I told him that I am a mathematician. He was stunned. What is so surprising in meeting a mathematician at a math department picnic?
Now I think I understand what happened. It never occurred to him that I was a mathematician. I was clearly unattached, so he couldn't place me as someone's wife. As the picnic was at Ingrid's house, he must have concluded that I had to be Ingrid's relative. Very logical, but very gender biased.
I heard this problem many years ago when I was working for Math Alive.
Three men are fighting in a truel. Andrew is the worst shot; he misses 2/3 of the time. Bob is better; he misses 1/3 of the time. Connor is the best shot; he always hits. Each of the three men have an infinite number of bullets. Each shot is either a kill or a miss. They have to shoot at each other in order until two of them are dead. To make it more fair they decide to start with Andrew, followed by Bob, and then Connor. We assume that they choose their strategies to maximize their probability of survival. At whom should Andrew aim for his first shot?
This is a beautiful probability puzzle, and I will not spoil it for you by writing a solution. Recently, I watched an episode of Numb3rs: The Fifth Season ("Frienemies") which featured a version of this puzzle. Here is how Dr. Marshall Penfield, a frienemy of the protagonist Charlie Eppes, describes it:
Imagine a duel between three people. I'm the worst shot; I hit the target once every three trials. One of my opponents [Charlie] is better; hits it twice every three shots. The third guy [Colby] is a dead shot; he never misses. Each gets one shot. As the worst I go first, then Charlie, then Colby. Who do I aim for for my one shot?
This is a completely different problem; it's no longer about the last man standing. Colby doesn't need to shoot since the other two truelists have already expended their only shots. If Charlie believes that Colby prefers nonviolence, all else being equal, then Charlie doesn't need to shoot. Finally, the same is true of Marshall. There is no point in shooting at all.
To make things more mathematically interesting, let's assume that the truelists are bloodthirsty. That is, if shooting doesn't decrease their survival rate, they will shoot. How do we solve this problem?
If he survives, Colby will kill someone. If Charlie is alive during his turn, he has to shoot Colby because Colby might kill him. What should Marshall do? If Marshall kills Colby, then Charlie misses Marshall (hence Marshall survives) with probability 1/3. If Marshall kills Charlie, then Marshall is guaranteed to be killed by Colby, so Marshall survives with probability 0. If he doesn't kill anyone, things look much better: with probability 2/3, Colby is killed by Charlie and Marshall survives. Even if Colby is alive, he does not necessarily shoot Marshall, so Marshall survives with probability at least 2/3. Overall, Marshall's chances of staying alive are much better if he misses. He should shoot in the air!
The sad part of the story is that Charlie Eppes completely missed. That is, he completely missed the solution. In the episode he suggested that Marshall should shoot Charlie. If Marshall shoots Charlie, he will be guaranteed to die.
It is disappointing that a show about math can't get its math right.
From the 1966 Moscow Math Olympiad:
Prove that you can choose six weights from a set of weights weighing 1, 2, …, 26 grams such that any two subsets of the six have different total weights. Prove that you can't choose seven weights with this property.
Let us define the sequence a(n) to be the largest size of a subset of the set of weights weighing 1, 2, …, n grams such that any subset of it is uniquely determined by its total weight. I hope that you agree with me that a(1) = 1, a(2) = 2, a(3) = 2, a(4) = 3, and a(5) = 3. The next few terms are more difficult to calculate, but if I am not mistaken, a(6) = 3 and a(7) = 4. Can you compute more terms of this sequence?
Let's see what can be said about upper and lower bounds for a(n). If we take weights that are different powers of two, we are guaranteed that any subset is uniquely determined by the total weight. Thus a(n) ≥ log2n. On the other hand, the total weight of a subset has to be a number between 1 and the total weight of all the coins, n(n+1)/2. That means that our set can have no more than n(n+1)/2 subsets. Thus a(n) ≤ log2(n(n+1)/2).
Returning back to the original problem we see that 5 ≤ a(26) ≤ 8. So to solve the original problem you need to find a more interesting set than powers of two and a more interesting counting argument.
Fifteen years ago I attended Silvio Micali's cryptography course. During one of the lectures, he asked me to close my eyes. When I did, he wrote a random sequence of coin flips of length six on the board and invited me to guess it.
I am a teacher at heart, so I imagined a random sequence I would write for my students. Suppose I start with 0. I will not continue with zero, because 00 looks like a constant sequence, which is not random enough. So my next step would be sequence 01. For the next character I wouldn't say zero, because 010 seems to promise a repetitive pattern 010101. So my next step would be 011. After that I do not want to say one, because I will have too many ones. So I would follow up with 0110. I need only two more characters. I do not want to end this with 11, because the result would be periodic, I do not want to end this with 00, because I would have too many zeroes. I do not want to end this with 01, because the sequence 011001 has a symmetry: reversing and negating this sequence produces the same sequence.
During the lecture all these considerations happened in the blink of an eye in my mind. I just said: 011010. I opened my eyes and saw that Micali had written HTTHTH on the board. He was not amused and may even have thought that I was cheating.
Many teachers, when writing a random sequence, do not flip a coin. They choose a sequence that looks "random": it doesn't have too many repetitions and the number of ones and zeroes is balanced (that is, approximately the same). When they write it character by character on the board, they often choose a sequence so that any prefix looks "random" too.
As a result, the sequence they choose stops being random. Actually, they're making a choice from a small set of sequences that look "random". So the fact that I guessed Micali's sequence is not surprising at all.
If you have gone to many math classes, you've seen a lot of professors choosing very similar-looking "random" sequences. This discriminates against sequences that do not look "random". To restore fairness to those under-represented sequences, I have decided that the next time I need a random sequence, I will choose 000000.
Two month ago I made a minor rearrangement of my math humor page. The traffic to that page tripled. Would you like to know what I did? I collected all the suggestive jokes in one chapter and named it Dirty Math Jokes.
Mathematics is so far from sex that stumbling on a math sex joke is always a special treat.
Combinatorialists do it discretely.
When those jokes were randomly placed in my joke file, it was easy to miss flirtatious connotations.
She was only a mathematician's daughter, and she sure learned how to multiply using square roots.
So I decided to collect them together in one place.
Math Problem: A mother is 21 years older than her son. In 6 years she will be 5 times as old as her son. Where is the father?

Sergei Bernstein and Nathan Benjamin brought back a variation of the "Rock, Paper, Scissors" game from the Mathcamp. They call it "Rock, Paper, Scissor." In this variation one of the players is not allowed to play Scissors. The game ends as soon as someone wins a turn.
Can you suggest the best strategy for each player?
They also invented their own variation of the standard "Rock, Paper, Scissors." In their version, players are not allowed to play the same thing twice in a row.
If there is a draw, then it will remain a draw forever. So the game ends when there is a draw. The winner is the person who has more points.
They didn't invent a nice name for their game yet, so I am open to suggestions.
Let me describe a variation of Nim that is at the same time a variation of Chomp. Here's a reminder of what Nim and Chomp are.
In the game of Nim, there are several piles of matches and two players. Each of the players, in turn, can take any number of matches, but those matches must come from the same pile. The person who takes the last match wins. Some people play with a different variation in which the person who takes the last match loses.

Mathematicians do not differentiate between these two versions since the strategy is almost the same in both cases. The classic game of Nim starts with four piles that have 1, 3, 5 and 7 matches. I call this configuration "classic" because it is how Nim was played in one of my favorite movies, "Last Year at Marienbad". Recently that movie was rated Number One by Time Magazine in their list of the Top 10 Movies That Mess with Your Mind.
In the game of Chomp, also played by two people, there is a rectangular chocolate bar consisting of n by m squares, where the lowest left square is poisoned. Each player in turn chooses a particular square of the chocolate bar, and then eats this square as well as all the squares to the right and above. The player who eats the poisonous square loses.
Here is my Nim-Chomp game. It is the game of Nim with an extra condition: the piles are numbered. With every move a player is allowed to take any number of matches from any pile, with one constraint: after each turn the i-th pile can't have fewer matches than the j-th pile if i is bigger than j.
That was a definition of the Nim-Chomp game based on the game of Nim, so to be fair, here is a definition based on the game of Chomp. The game follows the rules of Chomp with one additional constraint: the squares a player eats in a single turn must all be from the same row. In other words, the chosen square shouldn't have a square above it.
The game of Nim is easy and its strategy has been known for many years. On the other hand, the game of Chomp is very difficult. The strategy is only known for 2 by m bars. So I invented the game of Nim-Chomp as a bridge between Nim and Chomp.
More and more I stumble upon the claim that the difference in individual personal choices between men and women is one of the main contributors to the gender gap in mathematical careers. Let me tell you some stories that I've heard that illustrate some choices that women made. The names have been changed.
Ann got her PhD in math at the same time as her husband. They both got job offers at places very far from each other. As Ann was pregnant, she decided not to accept her offer and to follow her husband. In two years she was ready to go back to research and she started to search for some kind of position at the University where her husband worked. At that time there was a nuptial rule that prevented two spouses from working at the same place. There was no other college nearby, and Ann's husband didn't yet have tenure and freaked out at the thought of changing his job. They decided to have a second child. After two more years of staying home, she felt completely disqualified and dropped the idea of research.
Olga was very passionate about her children's education. She felt that public education was insufficient and that parents needed to devote a lot of time to reading and playing with their kids. Her husband insisted that the children would be fine on their own and he refused outright to read to them or to participate in time-consuming activities. Olga took upon herself the burden she was hoping to share. At that same time, she started a tenure track position. In addition to all of this, she took her teaching very seriously. Her students loved her, but her paper-writing speed declined. She didn't get tenure and quit academia. Later, she realized that in fact her husband had shared her sense of the importance of their children's education, but he had played a power-game which left her doing all the work.
Maria told her husband Alex that she wanted a babysitter for their two children now that she was ready to get back to mathematics. Alex sat down with her to look at their finances. Before looking for a job Maria needed to finish her two papers. That meant they had to pay a babysitter even though Maria wasn't bringing in any money. Maria agreed to postpone her comeback until the kids went to kindergarten. She somehow finished her papers and found her first part-time job as an adjunct lecturer. Alex sat down with her again to discuss their finances. They calculated how much time she would need to prepare to teach after such a long break. The babysitter would cost more than her income. In addition, they would have to buy a second car and some professional clothes for Maria. They summed everything up: it appeared that they couldn't afford for her to take this job. Maria rejected the offer.
Two years later, Alex was offered an additional job as a part-time mathematical consultant. Instead of accepting it Maria's husband suggested that the company interview Maria, who was longing to return to work. Maria got an offer, but at half the fee her husband was offered. The manager explained this difference by pointing to her husband's superior work record. Maria and Alex sat down together again and calculated that it would more profitable for them as a couple if he took the job and dropped all his household responsibilities. Maria couldn't find a way to argue.
I recently wrote about my own decision to quit academia twelve years ago. Although what I really wanted to do was to work in academia, my family responsibilities took precedence.
Yes, personal choices are a great contributor to the gender gap in mathematical careers. I just do not like when people assume that women chose freely. Some choices we were cornered into making.
I was somewhat taken aback by the popularity of my earlier essay "Divisibility by 7 is a Walk on a Graph." Tanya tells me it got a good number of hits. The graph in that article is rather crude, and takes a bit of care to use, because the arrows go off in random directions from each node. So taking a hint from a commenter on the first graph, I redrew the graph, sacrificing planarity in favor of ease of use. Specifically, I arranged the black arrows in a counterclockwise circle, which makes them easy to follow.
The graph is used in the same way as the first graph. To find the remainder on dividing a number by 7, start at node 0, for each digit D of the number, move along D black arrows (for digit 0 do not move at all), and as you pass from one digit to the next, move along a single white arrow.
For example, let n = 325. Start at node 0, move along 3 black arrows (to node 3), then 1 white arrow (to node 2), then 2 black arrows (to node 4), then 1 white arrow (to node 5), and finally 5 black arrows (to node 3). Finishing at node 3 shows that the remainder on dividing 325 by 7 is 3.
I fancy it to be a little animal face.

I am a milk person. I can easily drink half a gallon of milk a day. The problem with half a gallon of milk a day is that it is about half of my target calorie intake. That is why I switched to the reduced-fat milk. It didn't taste good, but I was very proud of myself. That is, I was proud for about a year until I finally decided to read the labels. One serving of whole milk is 150 calories, while one serving of reduced-fat milk is 130 calories. All this year-long suffering saved me an insignificant 13%. Not to mention that the amount of sugar is the same.
I decided to look into this more closely. I went to my nearest super-market and checked the milk. The low-fat milk is 110 calories per serving, while non-fat milk is 90 calories.
If I had just reduced my milk intake by half, I would have consumed fewer calories than by replacing whole milk with non-fat milk, but I would have enjoyed it so much more. The lesson? Read the labels and do the math!
Forty years ago, it took about 18 months for us to find the rules that eventually became the Game of Life. We thought in terms of birth rules and death rules. Maybe one day's death rule would be a bit too strong compared to its birth rule. So the next day at coffee time we'd either try to weaken the death rule or strengthen the birth rule, but either way, only by a tiny bit. They had to be extremely well-balanced; if the death rule was even slightly too strong then almost every configuration would die off. And conversely, if the birth rule was even a little bit stronger than the death rule, almost every configuration would grow explosively.
What's wrong with that, you might ask. Well, if the "radius" grows by 1 unit per generation, then after 9 or 10 moves, it's off the (19 by 19) Go board. We can probably find more Go boards, of course, but after another 20 or so moves it will outflow the coffee table and then it is awfully hard to keep track. We wanted to be able to study configurations for much longer than that, which meant that we had to disallow rules that might lead to linear growth. Of course, we weren't interested in rules that usually led to collapse.
Who were "we"? Well, I was the chief culprit and had an aim in mind — to find a simple set of rules that would lead to a system able to simulate a universal computer. Von Neumann had already shown that this was possible, but his system had 29 states and a very complicated set of rules. The rest of "us" were mostly graduate students who had no higher aim than amusing themselves. Every now and then some rather older colleagues or visitors took an interest.
So my plan was, first, to find a set of rules that almost always prevented explosive growth and catastrophic collapse. Second, I wanted to study it long enough to learn how it could be "programmed". I hoped to find a system whose rules were much simpler than Von Neumann's, preferably with only two states (on and off) per cell, rather than his 29.
I'll just describe the last few rule fiddles. We had in fact given up on finding a two-state system, in favor of one with three states: 0, A, B. State 0 represented an empty cell, and it was natural to think of A and B as two sexes, but we only found their proper names when Martin Huxley walked by and said, "Actresses and bishops!"
Perhaps I should explain this. There is a British anecdote that starts like this:
"The actress sat on the left side of the bed, and removed her stockings. The bishop, on the right side of the bed, removed his gaiters. Then she unbuttoned her blouse and he took off his shirt…"
You are supposed to be getting excited, but it all ends quite tamely, because it turns out that the bishop was in his palace, while the actress was in her bedsit near the theater. There are lots of stories in England about the actress and the bishop, and if a person says something that has a salacious double meaning, it's standard to respond "as the actress said to the bishop," or "as the bishop said to the actress".
Okay, back to Life! To inhibit explosive growth, we decided to imitate biology by letting death be a consequence of either overcrowding or isolation. The population would only grow if the number of neighbors was neither too large nor too small. Rather surprisingly, this turned out to mean that children had to have three or more parents. Let's see why. If two parents could give birth, then in the figure below, the parents A and B, who are on the border of the population, would produce children A' and B' at the next time step, followed by grandchildren A" and B" and so on, thus giving us linear growth!

So we moved to threesomes. Children were born to three parents, made up of both sexes. Moreover, the sex of the child was determined by the sex of its parents — two bishops and one actress would give birth to a little actress, while two actresses and one bishop would produce a tiny bishop. This was "the weaker-sex birth rule," and it was accompanied by "the sexual frustration death rule," which made death the punishment for not touching somebody of the opposite sex!
However, the weaker-sex birth rule lived up to its name, by being weaker than the death rule. Remember we weren't interested in rules that led to disappointingly swift collapses, as the actress said to the bishop. Therefore, we strengthened the birth rule by allowing same-sex conception, but again by applying the weaker-sex rule — so that three actresses would produce a bishop or three bishops an actress. However this strengthened the birth rule too much, causing us to apply the death penalty more often.
We decided to apply the death penalty to those who weren't touching at least two other people, whatever their sex. At first sight it was not obvious that this was stronger than the sexual frustration rule, but in fact it was, because the weaker-sex rule ensured that the sexes were fairly evenly mixed, so if you were touching at least two other people, there was a good chance that one of them would be of the opposite sex.
According to our new set of rules, the sex of parents played no role except to determine the sex of the children, so we abolished sex. After all, according to the bishop, Life without sex is much cleaner.
This is now called the Game of Life and these rules, at last, turned out to be clean and well-balanced.
The article Daring to Discuss Women in Science by John Tierney in the New York Times on June 7, 2010 purports to present a dispassionate scientific defense of Larry Summers's claims, in particular by reviewing and expanding his argument that observed differences in the length of the extreme right tail of the bell curves of men's and women's test scores indicate real differences in their innate ability. But in fact any argument like this has to acknowledge a serious difficulty: it is problematic to assume without comment that the abilities of a group can be inferred from the tail of a bell curve. We are so used to invoking bell curves to talk about group abilities, we don't notice that such arguments usually use only the mean of the curve. Using the tail is a totally different story.
Think about it: it is reasonable to question whether a single data point — the test score of an individual person — is a true indication of his/her ability. It might not be. Maybe a single test score represents a dunce with hyper-overachieving parents who push him to study all the time. So does that single false reading destroy the validity of the curve? No of course not: because some other kid might have been a super-genius who was drunk last night and can barely keep his eyes open during the test. One is testing above his "true ability" and the other is testing below his "true ability," and the effect cancels out. Thus the means of curves are a good way to measure the ability of large groups, because all the random false readings average out.
But tails are not. On the tail this "canceling out" effect doesn't work. Look at the extreme right tail. The relatively slow but hyper-motivated kids are not canceled out by the hoard of far-above-the-mean super geniuses who had drunken revels the night before. There just aren't that many super-geniuses and they just don't party that much.
Or let's look at it another way: imagine that you had a large group which you divided in half totally at random. At this point their bell curve of test scores looks exactly the same. Lets call one of the group "boys" and the other group "girls". But they are two utterly randomly selected groups. Now lets inject the "boys" with a chemical that gives the ones who are very good already a burning desire to dominate any contest they enter into. And let us inject the "girls" with a chemical that makes the ones who are already good nonetheless unwilling to make anyone feel bad by making themselves look too good. What will happen to the two bell curves? Of course the upper tail of the "boys'" curve will stretch out, while the "girls'" tail will shrink in. It will look like the "boys" whipped the "girls" on the right tail of ability hands down, no contest. But the tail has nothing to do with ability. Remember they started out with the same distribution of abilities, before they got their injections. It is only the effect of the chemicals on motivation that makes it look like the "boys" beat the "girls" at the tail.
So, when you see different tails, you can't automatically conclude that this is caused by difference in underlying innate ability. It is possible that other factors are at play — especially since if we were looking to identify these hypothetical chemicals we might find obvious candidates like "testosterone" and "estrogen".
The possibility of alternative explanations for these findings calls into question Tierney and Summers' claims to superior dispassionate scientific objectivity. Moving from the mean to the tail of a bell curve makes systematic effects on averages irrelevant, true, but it is instead susceptible to systematic effects on deviations, which are irrelevant at the mean. An argument that uses this trick to dodge gender differences in averages cannot claim the mantle of scientific responsibility without accounting for gender differences in deviations. I am deeply disappointed that Tierney and Summers did not accompany their assertions with a suitable reminder of this fact.
I recently published a puzzle about wizards, hats of different colors and rooms. Unfortunately, I was too succinct in my description and didn't explicitly mention several assumptions. Although such assumptions are usual in this type of puzzle, I realize now, from your responses, that I should have listed them and I apologize.
The Sultan decided to test the wisdom of his wizards. He collected them together and gave them a task. Tomorrow at noon he will put hats of different colors on each of the wizard's heads.
The wizards have a list of the available colors. There are enough hats of each color for every wizard. The wizards also have a list of rooms. There are enough rooms to assign a different room for every color.
Tomorrow as the Sultan puts hats on the wizards, they will be able to see the colors of the hats of the other wizards, but not the color of their own. Without communicating with each other, each wizard has to choose a room. The challenge comes when two wizards have the same hat color, for they must choose the same room. On the other hand, if they have different hat colors, they must choose different rooms. Wizards have one day to decide on their strategy. If they do not all complete their task, then all of their heads will be chopped off. What strategy would you suggest for the wizards?
In his comment on the first blog about this problem, JBL beautifully described the intended solution for the finite number of wizards, and any potentially-infinite number of colors. I do not want to repeat his full solution here. I would rather describe his solution for two wizards and two colors.
Suppose the colors are red and blue. The wizards will designate one of the rooms as red and another as blue. As soon as each wizard sees the other wizard's hat color, he chooses the room of the color he sees. The beauty of this solution is that if the colors of hats are different, the color of the rooms will not match the color of the corresponding hats: the blue-hatted wizard will go to the red room and vice versa. But the Sultan's condition would still be fulfilled.
JBL's solution doesn't work if the number of wizards is infinite. I know the solution in that case, but I do not like it because it gives more power to the axiom of choice than I am comfortable with. If you are interested, you can extrapolate the solution from my essay on Countable Wise Men with Hats which offers a similar solution to a slightly different problem.
The International Math Olympiad started in Eastern Europe in 1959. Romania was the first host country. The Olympiad grew and only in 1976 did it move outside the Eastern bloc. The competition was held in Austria.
I was on the Soviet team in 1975 and 1976, so I was able to compare competitions held in Eastern vs. Western countries. Of course, the Austrian Olympiad was much better supported financially, but today I want to write about the differences in how our team was prepped.
Before our travel to Austria the Soviet team members were gathered in a room with strangers in suits for a chat. I assumed that we were talking to the KGB. They gave us a series of instructions. For example, they told us not to leave the campus during the competition, to always walk in groups, and to avoid talking to kids from countries that are enemies of the USSR. They warned us that they would be watching, and I was scared to death.
Now that I am older and wiser, I understand that their goal was to frighten us. Our team traveled with adult supervisors, who were trusted by the KGB. But for several days during the grading period of the competition, our supervisors were not allowed to see us. So the KGB wanted us to be too afraid to be very adventurous when we were left on our own.
In addition, the KGB had a Jewish problem. In general, Jews were not allowed to go abroad. I had many Jewish friends who qualified for the pre-IMO math camp where the team was chosen, but who were not able to get on the IMO because of delays with their travel documents. Some local bureaucrats were eager to impress the KGB and therefore held up visas for Jewish students, preventing them from being on the team. But the team selection process itself wasn't yet corrupt in 1976. So every year despite the efforts of the system, some young Jewish mathematicians would end up on the team.
Before 1976, the Olympiad was in the Eastern bloc, so the KGB wasn't quite so concerned about having Jewish members on the team. But Austria was not only a Western country, it was also the transition point for Jewish refugees from the Soviet Union. The speed with which the IMO moved their competition to a Western country was much faster than the Soviet bureaucratic machine could build a mechanism for completely preventing Jews from joining the team.
One very strong candidate, Yura Pass, didn't get his documents, but two other Jewish boys made it on to the team that was going to Austria. They were joking that they would be the only Soviet Jews who would go to Austria and actually come back. They did come back, only to go forward later: both are now math professors working in the US.
Because we had Jewish members on our team, it gave the KGB a special extra reason to scare us. But the biggest pressure was to win. We were told that 1976 was the most important year for the Soviet team to be the best. We were told that capitalist countries spread rumors that the judges in Eastern bloc countries favored the Soviet team and that the relative success of the Soviet team throughout the years had not been fully deserved. Now that the competition was in Austria, the suits told us, the enemies of the USSR were hoping for the downfall of the Soviet team. Our task was to prove once and for all that the Soviet students were the best at math, and that the rumors were unfounded. We had to win the team competition not only to prove ourselves, but also to clear the name of the Soviet team for all the previous years.
We did have a very strong team. The USSR came out first with 250 points, followed by the UK with 214 points and the USA with 188 points. Out of nine gold medals, we took four.
We could have gotten one more gold medal if Yura Pass had been allowed on the team. Yura was crushed by the machine's treatment of Jews and soon afterwards quit mathematics.
I just received a mass email on how to live longer and it made these points:
Tip 1. Delay your retirement. Studies show that people who retire at 65 live longer than people who retire at 60.
Tip 2. Sex makes you younger. Studies show that older people who have sex twice a week look ten years younger than their peers who do not have sex at all.
People who draw conclusions from such studies usually do not understand statistics. Correlation doesn't mean causality. Let me use the above-mentioned studies to reach different conclusions by reversing the causality assumption of the unknown writer of the mass email. You can compare results and make your own decisions.
Case 1. Studies show that people who retire at 65 live longer than people who retire at 60. Reversed causality: People who live longer are healthier, so they are able to keep working and to retire later in life.
Case 2. Studies show that older people who have sex twice a week look ten years younger than their peers who do not have sex at all. Reversed causality: Older people who look ten years younger than their peers can get laid easier, so they have sex more often.
Sergei just came back from MOP — Mathematical Olympiad Summer Program, where he was a grader. The first question I asked him was, "What was your favorite math problem there?" Here it is:
There are wisemen, hats and rooms. Hats are of different color and there are enough hats of each color for every wisemen. There are enough rooms, so that you can assign a different room for every color. At some moment in time the sultan puts hats on the wisemen's heads, so as usual they see all other hats, but do not see their own hat color. At the same time, each wiseman has to choose a room to go to. If two wisemen have the same hat color, they should go to the same room. If they have different hat colors, they should go to different rooms. What strategy should the wisemen decide upon before this event takes place?
Oh, I forgot to mention the most interesting part of this problem is that you shouldn't assume that the number of wisemen or hats or rooms is finite. You should just assume that they have the power of choice.
My son Alexey Radul and I were discussing the Tuesday's child puzzle:
You run into an old friend. He has two children, but you do not know their genders. He says, "I have a son born on a Tuesday." What is the probability that his second child is also a son?
Here is a letter he wrote me on the subject. I liked it because unlike many other discussions, Alexey not only asserts that different interpretations of the conditions in the puzzle form different mathematical problems, but also measures how different they are.
If you assume that boys and girls are symmetric, and that days of the week are symmetric (and if you have no information to the contrary, assuming anything else would be sheer presumption on your part), then you can be in one of at least two states.
1) You say that "at least one son born on a Tuesday" is all the information you have, in which case your distribution including this information is uniform over consistent cases, in which case your answer is 13/27 boy and your information entropy is
− ∑27 (1/27) log(1/27) = − log(1/27) = 3.2958.
2) You say that the information you have is "The guy might have said any true thing of the form 'I have at least one {boy/girl} born on a {day of the week}', and he said 'boy', 'Tuesday'." This is a different mathematical problem with a different solution. The solution: By a symmetry argument (see below [*]) we must assign uniform probability of him making any true statement in any particular situation. Then we proceed by Bayes' Rule: the statement we heard is d, and for each possible collection of children h, the posterior is given by p(h|d) = p(h)p(d|h)/p(d). Here, p(h) = 1/142 = 1/196; p(d) = 1/14; and p(d|h) is either 1 or 1/2 according as whether his other child is or is not another boy also born on a Tuesday (or p(d|h) = 0 if neither child is a boy born on a Tuesday). There are 1 and 26 of these situations, respectively. The answer they lead to is of course 1/2; but the entropy is
− ∑ p log p = − 1/14 log 1/14 − 26/28 log 1/28 = 3.2827
Therefore that assumed additional structure really is more information, which is only present at best implicitly in the original problem. How much more information? The difference in entropies is 3.2958 - 3.2827 = 0.0131 nats (a nat is to a bit what the natural log is to the binary log). How much information is that? Well, the best I can do is to reproduce an argument of E.T. Jaynes', which may or may not really apply to this situation. Suppose you have some repeatable experiment with some discrete set of possible outcomes, and suppose you assign probabilities to those outcomes. Then the number of ways those probabilities can be realized as frequencies counted over N trials is proportional to eNH, where H is the entropy of the distribution in nats. Which means that the ratio by which one distribution is easier to realize is approximately eN(H1-H2). In the case of N = 1000 and H1 - H2 = 0.0131, that's circa 5x105. For each way to get a 1000-trial experiment to agree with version 2, there are half a million ways to get a 1000-trial experiment to agree with version 1. So that's a nontrivial assumption.
[*] The symmetry argument: We are faced with the following probability assignment problem
Suppose our subject's first child is a boy born on a Tuesday, and his second child is a girl born on a Friday. What probability must we assign to him asserting that he has at least one boy born on a Tuesday?
Good question. Let's transform our coordinates: Let Tuesday' be Friday, Friday' be Tuesday, boy' be girl, girl' be boy, first' be second and second' be first. Then our problem becomes
Suppose our subject's second' child is a girl' born on a Friday', and his first' child is a boy' born on a Tuesday'. What probability must we assign to him asserting that he has at least one girl' born on a Friday'?
Our transformation necessitates p(boy Tuesday) = p(girl' Friday'), and likewise p(girl Friday) = p(boy' Tuesday'). But our state of complete ignorance about what's going on with respect to the man's attitudes about boys, girls, Tuesdays, Fridays, and first and second children has the symmetry that question and question' are the same question, and must, by the desideratum of consistency, have the same answer. Therefore p(boy Tuesday) = p(boy' Tuesday') = p(girl Friday) = 1/2.
My classmate Misha gave me a math problem. Although I liked the math part, I hated the setup. Here is the problem using the new setup:
You are hoping to get very rich one day and you base your hopes on your new invention: a diet pill. The pill works beautifully and doesn't have side effects. Patients simply take a pill when they get hungry. Within one hour they will fall asleep and will be unable to awake for exactly two hours, at which time they will awake by themselves feeling completely sated.
You have just arrived at your lab, when you realize that one of your interns has misplaced your bottle of wonder pills. After some investigation, you come to the conclusion that your bottle is on the shelf with 239 other bottles that contain a placebo. Unfortunately, those placebo bottles were custom-designed for your statistical tests to exactly match your medicine bottle.
You need to bring the medicine bottle to your boss in two hours. While you panic, all your five interns volunteer for experiments, hoping to be mentioned in your paper. Can you find your bottle in two hours?
The problem Misha gave me had 240 barrels of wine, one of which contained deadly poison and five slaves who could be spared.
I do not like killing people even when they are imaginary. But while I was slow in inventing my own setup, the original version of the puzzle started making the rounds on the Internet. So I decided to kill the problem by writing the solution.
The strategy is to give out some pills immediately, wait for one hour and see who falls asleep. The next step is to give some other pills at the beginning of the next hour to some of the interns who are awake.
Let's count the information you can get out of this. Each intern will experience one of three different situations: falling asleep in the first hour, in the second hour, or not falling asleep at all. Thus, you can have a total of 35 = 243 different outcomes.
If you had more bottles than 243, there would be no way to distinguish between them. The fact that you have 240 bottles might mean that 243 will work too, but apparently the designer of the puzzle didn't want to hint into powers of three and picked the largest round number below 243. These considerations should increase your willingness to look into this problem base 3.
Let us label the bottles with different 5-character strings containing three characters 0, 1, and 2. Now we can use the label as instructions. The first character will be associated with the first intern and so on. Suppose the fourth character on the bottle's label is 0, then the fourth intern doesn't need to struggle with digesting a pill from this particular bottle. If the fourth character is 1, then the fourth intern gets the pill in the first hour. If the fourth character is 2, the fourth intern gets the pill in the second hour.
Note this minor detail: Suppose the fourth character on a bottle is 2, but the fourth intern is asleep by the second hour. That means, the bottle doesn't contain the medicine, and we can put it aside.
At the end of two hours you know who fell asleep and when. This data will exactly match the label on the bottle with the medicine.
Once I read a book in Russian that mentioned a study of the children of Soviet military personnel who had to move often. The conclusion was that frequent relocation is very damaging for children's psyche. The children had to build new friendships, which they would lose the next time they had to move. After several moves they would stop making friends; later, as adults, they would be afraid of getting close to anyone.
In September 1996, my husband, my two children and I came to Princeton from Israel for my husband's month-long visit to the Institute for Advanced Study. After the visit we were supposed to go back to Israel, but that didn't happen. My husband returned alone and I stayed in Princeton with my children. That's a long and sentimental story for another time.
Meanwhile, my older son Alexey started going to Princeton High School. By this time he had attended seven schools in three different countries. In light of the evidence presented in that book about the impact on children of moving, I felt very guilty. Alexey was entering 10th grade. Moving him again not only would further damage his ability to make friends, but would also screw up his college chances. He needed a stable environment leading up to college. For example, recommendation letters are better written by people who are involved with kids for several years. I was afraid to mess up his future. I promised myself not to move him again during high school, especially as Princeton High School was one of the best public schools in New Jersey.
At the same time, I got a Visiting Scholar position at Princeton University. Although it didn't pay me any salary, through that position I received university housing, library privileges and an office. I was living on my personal savings and the monthly check my husband was sending me from Israel. My money was running out and I felt completely lost, like so many immigrants. I was new to Princeton; I didn't have friends there; and I was struggling with English. On top of that, I had medical problems, not the least very low energy.
Ingrid Daubechies noticed me at the Princeton math department and approached me. After our conversation, she found some money for me to work on the Math Alive course she was designing. That work was a breath of fresh air. I enjoyed it tremendously, but the part-time salary was not enough. Then I received more help from Ingrid. She appreciated my work on Math Alive a lot, but realized that I needed a different solution. She sacrificed her own interests and started recommending me around. She arranged an interview for me at Telcordia, who offered me a job as a systems engineer.
The decision to accept this job was very painful, because I did not want to leave academia. However, considering that my priority was to keep Alexey in Princeton High School, I didn't feel I had other options. I knew that I couldn't stay much longer at Princeton University and I was aware that getting a University job often requires relocation.
Looking back, I think the reasons behind this decision were more complex than sacrificing my career for my child. If I had known more about social supports for poor families and about other possible research jobs, or if I had been more confident in my research abilities, I might not have left academics.
Alexey triumphed at Princeton High School. The school allowed him to take math courses at Princeton University. He took several, including the course in logic by John Conway and two courses in graph theory by Paul Seymour. Alexey's multi-variable calculus professor complained to me that she couldn't fit her grades into the required curve. If she gave Alexey 100%, the others would have to get less than 20. Luckily, it turned out that because her class was small, she didn't need to bother about making a curve. After three years in Princeton High School, Alexey secured an impressive resume and great recommendation letters and went to MIT to pursue a double major in mathematics and computer science.
Alexey translated from a Russian joke site:
American scientists finally developed a car that runs on water. Unfortunately, at the moment it only runs on water from the Gulf of Mexico.
I've heard about many mathematicians running polymath projects through their blogs. I wasn't planning to do that. It just happened. In this essay, I describe the collaborative effort that was made to solve the following problem that appeared in my blog on July 2009:
Baron Münchhausen has n identical-looking coins weighing 1, 2, …, n grams. The Baron's guests know that he has this set of coins, but do not know which one is which. The Baron knows which coin is which and wants to demonstrate to his guests that he is right. He plans to conduct weighings on a balance scale, so that the guests will be convinced about the weight of every of coin. What is the smallest number of weighings that the Baron must do in order to reveal the weights?
The sequence a(n) of the minimal number of weighings is called the Baron Münchhausen's omni-sequence to distinguish it from the Existential Baron's sequence where he needs the smallest amount of weighings to prove the weight of one coin of his choosing.
In this essay I will describe efforts to calculate a(n). The contributors are: Max Alekseyev, Ilya Bogdanov, Maxim Kalenkov, Konstantin Knop, Joel Lewis and Alexey Radul.
The sequence starts as a(1) = 0, because there is nothing to demonstrate. Next, a(2) = 1, since with only one weighing you can find which coin is lighter.
Next, a(3) = 2. Indeed you can't prove all the coins in one weighing, but in the first weighing you can show that the 1-gram coin is lighter than the 2-gram coin. In the second weighing you can show that the 2-gram coin is lighter than the 3-gram coin. Thus, in two weighings you can establish an order of weights and prove the weight of all three coins.
As you can see in the case of n = 3, you can compare coins in order and prove the weight of all the coins in n − 1 weighings. But this is not at all the optimal number. Let us see why a(4) = 2. In his first weighing the Baron can put the 1- and the 2-gram coins on the left pan of the balance and the 4-gram coin on the right pan. In the future, I will just describe that weighing as 1 + 2 < 4. This way everyone agrees that the coin on the right pan is 4 grams, and the coin that is left out is 3 grams. The only thing that is left to do is to compare the 1-gram and the 2-gram coins in the second weighing.
Later Konstantin Knop sent me a different solution for n=4. His solution provides an interesting example. While looking for solutions, people usually try to have an unbalanced weighing to be "tight". That is, they make it so that the heavier cup is exactly 1 gram heavier than the lighter cup. If you are trying to prove one coin in one weighing, "tightness" is a requirement. But it is not necessary when you have several weighings. Here is the first weighing in Konstantin's solution: 1 + 3 = 4; and his second second weighing is: 1 + 2 < 3 + 4. We see that the second weighing has a weight difference of four between pans.
Next, a(5) = 2. We can have the first weighing the same as before: 1 + 2 < 4, and the second weighing: 1 + 4 = 5. The second weighing confirms that the heavy coin on the right pan in the first weighing can't be the heaviest one, thus it has to be the 4-gram coin. After that you can see that every coin is identified.
Next, a(6) = 2. The first weighing, 1 + 2 + 3 = 6, divides all coins into three groups: {1,2,3}, {4,5} and {6}. We know to which group each coin belongs, but we do not know which coin in the group is which. The second weighing: 1 + 6 < 3 + 5, identifies every coin. Indeed, the only possibility for the left side to weigh less than the right side is when the smallest weighing coin from the first group and 6 are on the left, and the two largest weighing coins from the first two groups are on the right.
When I was writing my essay I suspected that n = 6 is the largest number for which a solution can be established in two weighings, but I didn't have any proof. So I was embarrassed to show my solutions of three weighings n equals 7, 8 and 9.
On the other hand I published the solutions suggested by my son, Alexey Radul, for n = 10 and n = 11. In these cases the theoretical lower bound of log3(n) for a(n) is equal to 3, and finding solutions in three weighings was enough to establish the value of the sequence a(n) for n = 10 and n = 11.
So, a(10) = 3, and here are the weighings. The first weighing is 1 + 2 + 3 + 4 = 10. After this weighing, we can divide the coins into three groups {1,2,3,4}, {5,6,7,8,9} and {10}. The second weighing is 1 + 5 + 10 < 8 + 9. After the second weighing we can divide all coins into groups we know they belong to: {1}, {2,3,4}, {5}, {6,7}, {8,9} and {10}. The last weighing contains the lowest weighing coin from each non-single-coin group on the left and the largest weighing coin on the right, plus, in order to balance them, the coins whose weights we know. The last weighing is 2 + 6 + 8 + 5 = 4 + 7 + 9 + 1.
Similarly, a(11) = 3, and the weighings are: 1 + 2 + 3 + 4 < 11; 1 + 2 + 5 + 11 = 9 + 10; 6 + 9 + 1 + 3 = 8 + 4 + 2 + 5.
After publishing my blog I wrote a letter to the Sequence Fans mailing list asking them to expand the sequence. Max Alekseyev replied with the results of an exhaustive search program he wrote. First of all, he found a counter-intuitive solution for n=6. Namely, the following two weighings: 1 + 3 < 5 and 1 + 2+ 5 < 3 + 6. He also confirmed that it is not possible to identify the coins in two weighings for n=7, n=8 and n=9.
So now I can stop being embarrassed and proudly present my solution for n=7 in three weighings. That is, a(7) = 3 and the first weighing is: 1+2+3 < 7, and it divides all the coins into three groups {1,2,3}, {4,5,6} and 7. The second weighing, 1 + 4 < 6, divides them even further. Now we know the identity of every coin except the group {2,3}, which we can disambiguate with the third weighing: 2 < 3.
In many solutions that I've seen, one of the weighings was very special: every coin on one cup was lighter than every coin on the other cup. I wondered if that was always the case. Konstantin Knop send me a counterexample for n=7. The first weighing is: 1 + 2 + 3 + 5 = 4 + 7. The second is: 1 + 2 + 4 < 3 + 5. The third is: 1 + 3 + 4 = 2 + 6.
Later Max Alekseyev sent me two more special solutions for n=7. The first one contains only equalities: 2 + 5 = 7; 1 + 2 + 4 = 7; 1 + 2 + 3 + 5 = 4 + 7. The second one contains only inequalities: 1 + 3 < 5; 1 + 2 + 5 < 3 + 6; 5 + 6 < 2 + 3 + 7.
Moving to the next index, a(8) = 3 and the first weighing is: 1 + 2 + 3 + 4 + 5 < 7 + 8. The second weighing is: 1 + 2 + 5 < 4 + 6. After that we have identified all coins but two groups {1,2} and {3,4} that can be resolved by 2 + 4 = 6.
Meanwhile my blog received a comment from Konstantin Knop who claimed that he found solutions in three weighings for n in the range between 12 and 17 inclusive and four weighings for n = 53. I had already corresponded with Konstantin and knew that his claims are always well-founded, so I didn't doubt that he had found the solutions.
Later I began to write a paper with Joel Lewis on the upper bound of the omni-sequence, where we prove that a(n) ≤ 2 ⌈log2n⌉. For this paper, we wanted a comprehensive set of examples, so I emailed Konstantin asking him to write up his solutions. He promptly sent me the results and mentioned that he had found the weighings together with Ilya Bogdanov. They used several different ideas in the solutions. First I'll describe their solutions based on ideas we've already seen, namely to compare the lightest coins in the range to the heaviest coins.
Here is the proof that a(13) = 3. The first weighing is: 1 + … + 8 = 11 + 12 + 13, and it identifies the groups {1, 2, 3, 4, 5, 6, 7, 8}, {9, 10} and {11, 12, 13}. The second weighing is: (1 + 2 + 3) + 9 + (11 + 12) = (7 + 8) + 10 + 13, and it divides them further into groups {1, 2, 3}, {4, 5, 6}, {7, 8}, {9}, {10}, {11, 12}, {13}. And the last weighing identifies all the coins: 1 + 4 + 7 + 11 + 9 + 10 = 3 + 6 + 8 + 12 + 13.
Similarly, let us show that a(15) = 3. The first weighing is: 1 + … + 7 < 14 + 15, and it divides the coins into three groups {1, 2, 3, 4, 5, 6, 7}, {8, 9, 10, 11, 12, 13}, and {14, 15}. The second weighing is: (1 + 2 + 3) + 8 + (14 + 15) = (5 + 6 + 7) + (12 + 13), and this divides them further into groups {1, 2, 3}, {4}, {5, 6, 7}, {8}, {9, 10, 11}, {12, 13} and {14, 15}. The third weighing identifies every coin: 1 + 5 + 8 + 9 + 12 + 14 = 3 + 7 + 11 + 13 + 15.
As I mentioned earlier it is not always possible to find the first weighing which will nicely divide the coins into groups. We already discussed an example, n = 5, in which neither of the two weighings divided the coins into groups. Likewise, the same thing happened in the second mysterious solution for n = 6. What these solutions have in common is that the first weighing nearly divides everything nicely. The left pan is almost the set of the lightest coins and the right pan is almost the set of the heaviest coins. But not quite.
That is not our only situation in which the first weighing does not quite divide the coins into groups. For example, here is Konstantin's solution for a(9) = 3. For the first weighing, we put five coins on the left pan and two coins on the right pan. The left pan is lighter. This could happen in three different ways:
The second weighing, 1 + 2 + 3 = 6, in which we took three coins from the left pan and balanced them against one coin – again from the left pan – could only happen in case "C." After the two weighings, the following groups were identified: {1, 2, 3}, {4}, {5, 7}, {6}, {8, 9}. The third weighing, 1 + 4 + 5 + 8 < 3 + 7 + 9, identifies all the coins.
A similar technique is used in the solution that Konstantin sent to us to demonstrate that a(12) = 3. The first weighing is: 1 + 2 + 3 + 4 + 5 + 6 < 10 + 12. The audience which sees the results of the weighings understands that there are three possibilities for the distribution of coins:
The second weighing, (1 + 2 + 3) + (7 + 8) + 10 < (9 + 11 ) + 12, convinces the audience that the left pan must weigh at least 31 if the first weighing was case "A" above (31 = 1 + 2 + 3 + 7 + 8 + 10) or "C" (31 = 1 + 2 + 3 + 6 + 8 + 11), and at least 32 (32 = 1 + 2 + 3 + 7 + 8 + 11) if the first weighing was case "B." At the same time the right pan is not more than 12 + 9 + 11 = 32 for case "A" above, not more than 12 + 9 + 10 = 31 for case "B" and not more than 12 + 9 + 10 = 31 for case "C."
Hence the inequality in the second weighing is only possible when the first weighing was indeed as described by case "A" above. Consequently, the first two weighings together identify groups: {1, 2, 3}, {4, 5, 6}, {7, 8}, {9}, {10}, {11} and {12}. The third weighing, 1 + 4 + 7 + 11 + 12 < 3 + 6 + 8 + 9 + 10, identifies all the coins.
Other cases that Konstantin Knop sent me used a completely different technique. I would like to explain this technique using the mysterious solution for n = 6 found by Max Alekseyev. Suppose we have six coins labeled c1, … c6. The first weighing is: c1 + c3 < c5. The second weighing is: c1 + c2 + c5 < c3 + c6.
Let us prove that these two weighings identify all the coins. Let us replace the two inequalities above with the following: c1 + c3 − c5 ≤ −1, and c1 + c2 + c5 − c3 − c6 ≤ −1. Now we multiply the first inequality by 3 and the second by 2 and sum the results. We get: 5c1 + 2c2 + c3 + 0c4 − c5 − 2c6 ≤ −5. Note that the coefficients for labels are in a decreasing order. By the rearrangement inequality the smallest value the expression 5c1 + 2c2 + c3 + 0c4 − c5 − 2c6 reaches is when the labels on the coins match the indices. This smallest value is −5. Hence, the labels have to match the coins.
The technique that Konstantin and his collaborators are using is to search for appropriate coefficients to multiply the weighings by, rather than searching for the weighings themselves. In lieu of lengthy explanations, I will just list the weighings that he uses together with coefficients to multiply them by for their proof that the weighings differentiate coins.
We will start with showing that a(14) = 3. The weighings are: 1 + 2 + 3 + 4 + 5 + 6 + 7 + 9 < 11 + 13 + 14, and: 1 + 2 + 3 + 8 + 11 + 13 = 7 + 9 + 10 + 12, followed by 1 + 4 + 7 + 10 = 3 + 6 + 13. The coefficients to multiply by are {9, 5, 2}.
Next we will show that a(16) = 3. The weighings are: 1 + 2 + 3 + 4 + 5 + 6 + 8 < 14 + 16, and 1 + 2 + 3 + 7 + 9 + 14 = 8 + 13 + 15, followed by 1 + 4 + 7 + 10 + 13 < 3 + 6 + 12 + 15. The coefficients to multiply by are {11, 5, 2}.
Next we will show that a(17) = 3. The weighings are: 1 + 2 + 3 + 4 + 5 + 6 + 7 + 9 + 10 < 15 + 16 + 17, and 1 + 2 + 3 + 8 + 11 + 15 + 16 < 7 + 9 + 10 + 14 + 17, and 1 + 4 + 7 + 8 + 12 + 14 = 3 + 6 + 10 + 11 + 16. The coefficients to multiply by are {11, 5, 2}.
Next we will show that a(53) = 4. The weighings are: (1 + 2 + … + 23) + 25 < 47 + (49 + … + 53), and (1 + … + 9) + 24 + (26+ … + 31) + 47 + (49 + … + 52) < (16 + … + 23) + 25 + (41 + … + 46) + 48 + (51 + 52), and (1 + 2 + 3) + (10 + 11) + (16 + 17 + 18) + 24 + (26 + 27) + (32 + 33 + 34) + (41 + 42 + 43) + 47 + 49 + 53 =(7 + 8 + 9) + 15 + (22 + 23) + 25 + (30 + 31) + (38 + 39) + 40 + (45 + 46) + 48 + (51 + 52), and the last one 1 + 4 + 7 + 10 + 12 + 16 + 19 + 22 + 24 + 28 + 30 + 32 + 35 + 38 + 41 + 45 + 47 + 51 + 53 < 3 + 6 + 9 + 11 + 14 + 18 + 21 + 25 + 27 + 29 + 34 + 37 + 40 + 43 + 48 + 49 + 50 + 52. The coefficients to multiply by are {43, 15, 5, 2}.
When I was working on the paper with Joel Lewis I re-established my email discussions about the Baron's onmi-sequence with Konstantin Knop. At that time Konstantin's colleague, Maxim Kalenkov, got interested in the subject and wrote a computer search program to find other solutions that can be proven with the rearrangement inequality. Thus, we know two more terms of this sequence.
The next known term is a(18) = 3. The weighings are: 1 + 2 + 4 + 5 + 7 + 10 + 12 = 9 + 15 + 17, and 1 + 3 + 4 + 6 + 9 + 11 + 17 = 7 + 12 + 14 + 18, and 2 + 3 + 7 + 8 + 9 + 14 + 15 = 4 + 10 + 11 + 16 + 17. The corresponding coefficients are: {8, 7, 5}.
Similarly, a(19) = 3. The weighings are: 1 + 2 + 3 + 4 + 5 + 7 + 8 + 10 + 13 = 16 + 18 + 19, and 1 + 2 + 3 + 6 + 9 + 11 + 16 = 8 + 10 + 13 + 17, and 1 + 4 + 6 + 8 + 12 + 18 = 3 + 7 + 11 + 13 + 15. The coefficients are {12, 7, 3}.
Maxim Kalenkov continued his search. He didn't find any new solutions in three weighings, but he found a lot of solutions in four weighings, namely for numbers from 20 to 58. Below are his solutions, with multiplier coefficients in front of every weighing:
a(20) ≤ 4
18: 1+2+3+4+5+10+14+16+18 = 6+7+11+12+17+20
19: 1+2+4+5+12+15+17+19 < 6+8+10+14+18+20
21: 2+6+11+17+18 = 4+9+10+15+16
26: 1+6+7+8+9+10+20 = 2+5+17+18+19
a(21) ≤ 4
18: 3+5+6+11+15+17+19 = 7+8+9+13+18+21
19: 4+6+9+13+16+18+20 = 1+7+11+12+15+19+21
21: 1+4+5+7+12+18+19 = 3+9+10+11+16+17
26: 1+2+3+7+8+9+10+11+21 = 4+5+6+18+19+20
a(22) ≤ 4
18: 3+5+6+12+15+17+20 = 7+8+10+13+18+22
19: 1+2+4+10+13+16+18+21 = 7+9+12+15+20+22
21: 1+6+7+18+19+20 = 2+3+10+11+12+16+17
26: 2+3+7+8+9+10+11+12+22 = 6+18+19+20+21
a(22) ≤ 4
18: 1+2+5+6+12+16+18+22 < 3+7+8+10+13+19+23
19: 1+3+4+6+10+17+19+21 = 7+9+12+14+16+23
21: 3+7+13+14+19+20 = 2+6+10+11+12+17+18
26: 2+7+8+9+10+11+12+23 = 19+20+21+22
a(24) ≤ 4
18: 1+3+6+12+17+19+21+23 < 2+4+7+8+10+13+15+20+24
19: 1+2+4+5+6+10+15+18+20+22 < 7+9+12+14+17+21+24
21: 4+7+13+14+20+21 = 3+6+10+11+12+18+19
26: 2+3+7+8+9+10+11+12+24 = 20+21+22+23
a(25) ≤ 4
18: 1+2+3+5+6+8+9+14+17+19+22 < 10+12+16+20+24+25
19: 2+6+7+9+12+16+18+20+23 = 10+11+14+15+17+22+24
21: 1+2+4+7+8+10+15+20+21+22 = 3+6+12+13+14+18+19+25
26: 3+10+11+12+13+14+24+25 = 2+7+8+9+20+21+22+23
a(26) ≤ 4
18: 1+2+3+5+6+8+9+14+18+20+23 = 10+12+15+21+25+26
19: 2+3+4+6+7+9+12+19+21+24 = 11+14+16+18+23+25
21: 7+8+15+16+21+22+23 = 2+6+12+13+14+19+20+26
26: 1+2+10+11+12+13+14+25+26 = 7+8+9+21+22+23+24
a(27) ≤ 4
18: 1+3+4+6+7+8+9+14+19+21+23+25 < 10+11+13+15+17+22+26+27
19: 1+2+3+5+7+9+13+17+20+22+24 < 4+10+12+14+16+19+23+26
21: 2+3+4+8+10+15+16+22+23 = 1+7+13+14+20+21+27
26: 1+10+11+12+13+14+26+27 = 3+8+9+22+23+24+25
a(28) = 4
18: 3+6+8+9+10+15+19+21+24+26 = 1+5+11+13+16+18+22+27+28
19: 1+4+5+7+9+10+13+18+20+22+25 = 3+6+11+12+15+17+19+24+27
21: 5+6+11+16+17+22+23+24 = 4+9+13+14+15+20+21+28
26: 1+2+3+4+11+12+13+14+15+27+28 = 10+22+23+24+25+26
a(29) = 4
18: 1+3+5+6+7+9+10+16+20+22+25+27 < 11+12+14+17+18+23+28+29
19: 4+8+10+14+18+21+23+26 = 2+3+6+11+13+16+20+25+28
21: 1+2+6+8+9+11+17+23+24+25 = 4+5+14+15+16+21+22+29
26: 2+3+4+5+11+12+13+14+15+16+28+29 = 8+9+10+23+24+25+26+27
a(30) = 4
18: 2+8+10+16+21+23+26+27+28 = 5+11+12+14+17+19+24+29+30
19: 2+4+5+7+9+14+19+22+24+28 = 11+13+16+18+21+26+29
21: 1+5+6+9+10+11+17+18+24+25+26 = 4+14+15+16+22+23+28+30
26: 1+3+4+11+12+13+14+15+16+29+30 < 9+10+24+25+26+27+28
a(31) = 4
18: 1+2+6+9+10+16+21+23+26+28+29 < 3+4+7+11+12+14+17+19+24+30+31
19: 1+2+4+7+14+19+22+24+27+29 < 6+9+11+13+16+18+21+26+30
21: 2+3+7+8+9+11+17+18+24+25+26 = 14+15+16+22+23+29+31
26: 1+3+4+5+6+11+12+13+14+15+16+30+31 = 2+24+25+26+27+28+29
a(32) = 4
18: 1+5+8+9+10+12+13+22+24+27+29 = 6+14+16+18+20+25+30+31
19: 4+6+10+11+13+16+20+23+25+28 = 1+2+8+15+19+22+27+30+32
21: 1+2+6+7+8+11+12+18+19+25+26+27 = 4+5+10+16+17+23+24+31+32
26: 1+2+3+4+5+14+15+16+17+30+31+32 < 11+12+13+25+26+27+28+29
a(33) = 4
18: 1+2+6+7+8+9+10+12+13+23+27+29+30 = 3+14+15+17+19+21+25+31+32
19: 1+2+10+11+13+17+21+24+25+28+30 = 4+6+8+14+16+20+23+27+31+33
21: 1+3+4+8+11+12+14+19+20+25+26+27 < 7+10+17+18+24+30+32+33
26: 3+4+5+6+7+14+15+16+17+18+31+32+33 = 11+12+13+25+26+27+28+29+30
a(34) = 4
18: 2+3+4+8+10+12+13+19+24+28+30+31 < 6+14+15+17+20+22+26+32+33
19: 1+2+3+5+6+9+11+13+17+22+25+26+29+31 = 4+8+14+16+19+21+24+28+32+34
21: 1+3+6+7+8+11+12+14+20+21+26+27+28 = 2+5+17+18+19+25+31+33+34
26: 1+2+4+5+14+15+16+17+18+19+32+33+34 = 3+11+12+13+26+27+28+29+30+31
a(35) = 4
18: 1+3+4+6+8+10+11+13+19+24+26+29+31+32 = 14+15+17+20+22+27+33+34+35
19: 1+4+7+9+11+12+17+22+25+27+30+32 = 6+14+16+19+21+24+29+33+35
21: 2+12+13+14+20+21+27+28+29+35 = 4+7+8+11+17+18+19+25+26+32+34
26: 1+2+3+4+5+6+7+8+14+15+16+17+18+19+33+34 = 12+13+27+28+29+30+31+32
a(36) = 4
18: 1+2+3+4+5+9+11+12+14+15+20+25+29+31+32 < 6+16+18+21+23+27+33+34+36
19: 1+2+4+5+6+8+10+12+13+15+18+23+26+27+30+32 < 16+17+20+22+25+29+33+35+36
21: 1+3+5+13+14+16+21+22+27+28+29+36 = 2+8+9+12+18+19+20+26+32+34+35
26: 2+6+7+8+9+16+17+18+19+20+33+34+35 = 5+13+14+15+27+28+29+30+31+32
a(37) = 4
18: 1+2+3+6+8+10+12+13+15+16+21+27+30+32+33 = 4+9+17+19+22+24+28+34+35+37
19: 1+2+3+7+9+11+13+14+16+19+24+26+28+31+33 = 5+6+10+17+18+21+23+30+34+36+37
21: 3+4+5+9+10+14+15+17+22+23+28+29+30+37 = 1+7+8+13+19+20+21+26+27+33+35+36
26: 1+4+5+6+7+8+17+18+19+20+21+34+35+36 = 3+14+15+16+28+29+30+31+32+33
a(38) = 4
18: 2+3+4+7+9+11+13+15+16+21+26+28+31+33+34 = 5+10+17+18+19+22+24+29+35+36+38
19: 1+3+4+8+10+12+13+14+16+19+24+27+29+32+34 = 7+11+17+21+23+26+31+35+37+38
21: 1+2+4+5+10+11+14+15+17+22+23+29+30+31+38 = 8+9+13+19+20+21+27+28+34+36+37
26: 5+6+7+8+9+17+18+19+20+21+35+36+37 = 4+14+15+16+29+30+31+32+33+34
a(39) = 4
18: 1+2+4+7+9+11+13+14+16+22+27+29+32+34+35 = 10+17+18+20+23+25+30+36+38+39
19: 2+3+4+8+10+12+14+15+20+25+28+30+33+35 = 5+7+11+17+19+22+24+27+32+37+38
21: 1+2+3+5+10+11+15+16+17+23+24+30+31+32+38 < 8+9+14+20+21+22+28+29+35+36+37
26: 1+5+6+7+8+9+17+18+19+20+21+22+36+37 = 15+16+30+31+32+33+34+35
a(40) = 4
18: 1+2+3+4+5+8+9+12+14+15+17+18+23+27+29+32+34+35 < 7+10+19+21+24+26+30+36+37+39+40
19: 1+3+4+5+7+10+13+15+16+18+21+26+28+30+33+35 < 6+8+12+20+23+25+27+32+36+38+39
21: 1+5+6+10+11+12+16+17+24+25+30+31+32+39 < 3+9+15+21+22+23+28+29+35+37+38
26: 2+3+6+7+8+9+19+20+21+22+23+36+37+38 = 5+16+17+18+30+31+32+33+34+35
a(41) = 4
18: 1+3+5+6+8+10+12+14+15+17+18+23+28+30+33+35+36 < 7+11+19+21+24+26+31+37+38+40+41
19: 1+2+4+5+6+7+9+11+13+15+16+18+21+26+29+31+34+36 = 8+12+19+20+23+25+28+33+37+39+40
21: 1+4+6+11+12+16+17+19+24+25+31+32+33+40 < 9+10+15+21+22+23+29+30+36+38+39
26: 2+3+7+8+9+10+19+20+21+22+23+37+38+39 = 6+16+17+18+31+32+33+34+35+36
a(42) = 4
18: 1+3+5+6+7+11+13+15+16+18+24+29+31+34+36+37 = 2+8+12+19+20+22+25+27+32+38+40+41
19: 1+2+4+6+7+10+12+14+16+17+18+22+27+30+32+35+37 = 3+13+19+21+24+26+29+34+39+40+42
21: 1+2+3+4+5+7+8+12+13+17+19+25+26+32+33+34+40 = 10+11+16+22+23+24+30+31+37+38+39
26: 2+3+8+9+10+11+19+20+21+22+23+24+38+39 = 7+17+18+32+33+34+35+36+37
a(43) = 4
18: 1+2+5+6+7+10+12+14+16+17+19+20+29+31+34+36+37 = 8+21+23+25+27+32+38+39+41+42
19: 2+4+5+6+7+8+11+15+17+18+20+23+27+30+32+35+37 = 10+14+22+26+29+34+38+40+41+43
21: 1+2+3+7+13+14+18+19+25+26+32+33+34+41 < 5+11+12+17+23+24+30+31+37+39+40
26: 1+3+4+5+8+9+10+11+12+21+22+23+24+38+39+40 < 7+18+19+20+32+33+34+35+36+37
a(44) = 4
18: 1+2+5+6+7+8+10+11+14+16+17+19+20+25+30+32+35+37+38 = 3+12+21+22+23+26+28+33+39+40+42+44
19: 1+2+3+7+8+12+15+17+18+20+23+28+31+33+36+38+44 = 9+10+14+21+25+27+30+35+39+41+42+43
21: 2+3+4+6+8+9+12+13+14+18+19+21+26+27+33+34+35+42 = 11+17+23+24+25+31+32+38+40+41+44
26: 1+3+4+5+9+10+11+21+22+23+24+25+39+40+41 = 8+18+19+20+33+34+35+36+37+38
a(45) = 4
18: 2+4+5+6+11+13+16+17+18+20+21+26+31+33+36+38+39 = 7+9+14+22+24+27+29+34+40+42+43+45
19: 1+2+4+6+9+12+14+18+19+21+24+29+32+34+37+39+45 = 8+11+16+23+26+28+31+36+40+41+42+44
21: 1+2+3+5+7+8+14+15+16+19+20+27+28+34+35+36+42 = 4+12+13+18+24+25+26+32+33+39+41+45
26: 1+3+4+7+8+9+10+11+12+13+22+23+24+25+26+40+41 = 19+20+21+34+35+36+37+38+39
a(46) = 4
18: 1+2+3+5+6+8+9+14+16+17+19+21+22+26+31+33+36+38+39 = 10+12+23+27+29+34+40+41+42+43+45
19: 2+4+6+7+8+9+12+15+18+20+22+29+32+34+37+39+45 = 3+11+14+17+23+24+26+28+31+36+40+42+44
21: 1+3+7+9+10+11+17+20+21+23+27+28+34+35+36+42 = 6+15+16+25+26+32+33+39+41+45+46
26: 1+2+3+4+5+6+10+11+12+13+14+15+16+23+24+25+26+40+41 = 9+20+21+22+34+35+36+37+38+39
a(47) = 4
18: 2+3+5+7+8+9+13+14+16+18+19+21+22+27+32+34+37+39+40 < 11+23+24+28+30+35+41+42+43+44+46
19: 1+3+6+7+8+9+11+17+19+20+22+30+33+35+38+40+46 < 5+10+13+16+23+25+27+29+32+37+41+43+45
21: 1+2+4+5+9+10+15+16+20+21+23+28+29+35+36+37+43 < 7+14+19+26+27+33+34+40+42+46+47
26: 1+2+3+4+5+6+7+10+11+12+13+14+23+24+25+26+27+41+42 < 9+20+21+22+35+36+37+38+39+40
a(48) = 4
18: 3+5+6+7+8+13+17+19+20+22+23+28+33+35+38+40+41 < 9+11+15+24+26+29+31+36+42+44+45+47
19: 1+4+6+8+11+14+15+18+20+21+23+26+31+34+36+39+41+47 < 3+10+13+17+24+25+28+30+33+38+42+43+44+46
21: 1+2+3+7+8+9+10+15+16+17+21+22+24+29+30+36+37+38+44 = 6+14+20+26+27+28+34+35+41+43+47+48
26: 1+2+3+4+5+6+9+10+11+12+13+14+24+25+26+27+28+42+43 = 8+21+22+23+36+37+38+39+40+41
a(49) = 4
18: 2+3+6+7+8+9+10+15+18+20+21+23+24+29+34+38+40+41+49 < 12+16+25+26+30+32+36+42+43+44+45+47
19: 1+3+5+7+9+10+12+14+16+19+21+22+24+32+35+36+39+41+47 < 11+18+25+27+29+31+34+38+42+44+46+49
21: 1+2+3+4+8+10+11+16+17+18+22+23+25+30+31+36+37+38+44 < 7+14+15+21+28+29+35+41+43+47+48+49
26: 1+2+4+5+6+7+11+12+13+14+15+25+26+27+28+29+42+43 = 10+22+23+24+36+37+38+39+40+41
a(50) = 4
18: 1+2+3+4+6+7+9+10+11+15+16+19+20+21+23+24+34+36+39+41+42+50 = 12+17+25+26+28+30+32+37+43+44+45+46+48
19: 2+3+5+7+8+10+11+17+21+22+24+28+32+35+37+40+42+48 = 4+13+15+19+25+27+31+34+39+43+45+47+50
21: 1+3+4+8+9+11+12+13+17+18+19+22+23+25+30+31+37+38+39+45 = 7+16+21+28+29+35+36+42+44+48+49+50
26: 1+2+4+5+6+7+12+13+14+15+16+25+26+27+28+29+43+44 = 11+22+23+24+37+38+39+40+41+42
a(51) = 4
18: 2+3+4+6+8+10+11+15+17+19+20+21+23+24+30+35+37+40+42+43+50 < 12+13+18+25+26+28+31+33+38+44+46+47+49+51
19: 1+3+4+7+9+11+13+16+18+21+22+24+28+33+36+38+41+43+49 < 6+15+19+25+27+30+32+35+40+45+46+48+50
21: 1+2+4+5+6+9+10+11+12+18+19+22+23+25+31+32+38+39+40+46+51 < 16+17+21+28+29+30+36+37+43+44+45+49+50
26: 1+2+3+5+6+7+8+12+13+14+15+16+17+25+26+27+28+29+30+44+45 < 11+22+23+24+38+39+40+41+42+43+51
a(52) = 4
18: 2+5+7+8+10+11+12+17+19+22+25+26+31+35+37+40+42+43+51 = 3+13+15+20+27+28+29+32+38+44+46+47+49+52
19: 1+2+3+6+8+9+11+12+15+18+20+23+24+26+29+36+38+41+43+49 = 5+14+17+22+27+31+33+35+40+45+46+48+51
21: 1+3+4+5+9+10+12+13+14+20+21+22+24+25+27+32+33+38+39+40+46+52 = 8+18+19+29+30+31+36+37+43+44+45+49+50+51
26: 1+2+3+4+5+6+7+8+13+14+15+16+17+18+19+27+28+29+30+31+44+45 = 12+24+25+26+38+39+40+41+42+43+52
a(53) = 4
18: 2+3+4+7+8+9+10+11+12+17+19+21+23+25+26+31+36+38+41+43+44+52 < 5+13+15+27+29+32+34+39+45+46+47+48+50+53
19: 1+3+4+5+9+11+12+15+18+22+23+24+26+29+34+37+39+42+44+50 = 7+14+17+21+27+28+31+33+36+41+45+47+49+52
21: 1+2+4+5+6+7+10+12+13+14+20+21+24+25+27+32+33+39+40+41+47+53 < 9+18+19+23+29+30+31+37+38+44+46+50+51+52
26: 1+2+3+5+6+7+8+9+13+14+15+16+17+18+19+27+28+29+30+31+45+46 = 12+24+25+26+39+40+41+42+43+44+53
a(54) = 4
18: 2+3+4+6+8+9+11+12+13+18+20+23+25+26+28+29+33+37+39+41+42+43+51 = 5+14+16+21+30+31+32+35+44+45+47+48+49+52+54
19: 1+3+4+5+7+9+10+12+13+16+19+21+24+26+27+29+32+35+38+43+49+54 < 6+15+18+23+30+33+34+37+41+44+46+47+51+53
21: 1+2+4+5+6+10+11+13+14+15+21+22+23+27+28+30+34+40+41+47+52+53 < 9+19+20+26+32+33+38+39+43+45+46+49+50+51
26: 1+2+3+5+6+7+8+9+14+15+16+17+18+19+20+30+31+32+33+44+45+46 < 13+27+28+29+40+41+42+43+52+53+54
a(55) = 4
18: 2+3+6+8+9+11+12+13+18+19+22+24+25+27+28+32+37+39+42+44+45+54 < 4+14+16+20+29+31+33+35+40+46+47+49+50+52+55
19: 1+2+3+4+7+9+10+12+13+16+20+23+25+26+28+31+35+38+40+43+45+52 < 6+15+18+22+30+32+34+37+42+46+48+49+51+54
21: 1+3+4+5+6+10+11+13+14+15+20+21+22+26+27+33+34+40+41+42+49+55 = 9+19+25+31+32+38+39+45+47+48+52+53+54
26: 1+2+4+5+6+7+8+9+14+15+16+17+18+19+29+30+31+32+46+47+48 = 13+26+27+28+40+41+42+43+44+45+55
a(56) = 4
18: 2+3+4+7+9+10+12+13+14+18+20+23+25+26+28+34+39+41+44+46+47+55 < 5+15+16+21+29+30+32+35+37+42+48+50+52+53+56
19: 1+3+4+5+8+10+11+13+14+16+19+21+24+26+27+28+32+37+40+42+45+47+52 < 7+18+23+29+31+34+36+39+44+49+51+54+55+56
21: 1+2+4+5+6+7+11+12+14+15+21+22+23+27+29+35+36+42+43+44+53+54 < 10+19+20+26+32+33+34+40+41+47+48+49+52+56
26: 1+2+3+5+6+7+8+9+10+15+16+17+18+19+20+29+30+31+32+33+34+48+49+56 = 14+27+28+42+43+44+45+46+47+53+54+55
a(57) = 4
18: 2+3+4+7+9+10+12+14+18+19+22+24+27+32+35+36+39+43+45+49+51 < 5+13+16+21+26+28+31+34+38+41+42+48+50+53+56
21: 1+3+4+5+8+10+11+14+16+18+20+21+25+29+31+35+38+40+41+46+51+53+57 < 7+15+19+24+26+30+36+37+39+42+45+47+48+52+55+56
25: 1+2+4+5+6+7+11+12+13+15+18+21+23+24+26+29+32+34+37+41+44+45+48+55 = 10+20+22+31+33+36+40+43+47+51+53+54+56+57
33: 1+2+3+5+6+7+8+9+10+13+15+16+17+19+20+22+26+28+30+31+33+36+42+47+56 = 18+29+32+35+41+44+45+46+49+51+55+57
a(58) = 4
17: 2+3+4+8+9+10+12+13+14+21+22+25+26+27+29+30+37+42+43+45+46+47+56 < 5+15+16+20+31+32+33+35+36+41+48+49+51+52+53+55
20: 1+3+4+5+7+10+11+13+14+16+19+20+24+27+28+30+33+36+40+41+44+47+53 = 8+17+21+25+31+37+38+42+45+48+50+51+56+57
21: 1+2+4+5+6+8+11+12+14+15+17+20+23+25+28+29+31+35+38+41+45+51+55+57 < 10+19+22+27+33+34+37+40+43+47+49+50+53+54+56
26: 1+2+3+5+6+7+8+9+10+15+16+17+18+19+21+22+31+32+33+34+37+48+49+50 < 14+28+29+30+41+44+45+46+47+55+57+58

You might ask why this piece is titled George Hart, when the only man in the photo on the left is John Conway. George Hart is related to this picture in three different ways.
First, this picture is of the math department common room at Princeton University. It was taken during a joint event of the WaM and SWIM programs in June, 2009. It shows the Zometool workshop conducted by George Hart that resulted in the construction of the expanded 120-cell, which appears in the photo's foreground.
The second connection to George Hart is that beautiful shiny object under the lights on the far left. The object is the propello-octahedron sculpture that George Hart created out of 150 CDs. The sculpture has been in the common room for many years, and I have always loved it.
Unfortunately, the sculpture was slowly degrading, even losing some of its parts. I visited Princeton in August 2008 and realized that the sculpture was facing a short life expectancy, so I took the picture of it that is below. I couldn't find any angle to shoot the photo that hid the lost pieces. The sculpture survived until my visit in June 2009, as evidenced by the first picture. But unfortunately it wasn't there any more during my last visit in May 2010.

Oops, I almost forgot. I promised you a third way in which George Hart relates to the first picture. He is the one who took it.
My coauthor Konstantin Knop publishes cute math problems in his blog (in Russian). Recently he posted a coin weighing problem that was given at the 2010 Euler math Olympiad in Russia to eighth graders. The author of the problem is Alexander Shapovalov.
Among 100 coins exactly 4 are fake. All genuine coins weigh the same; all fake coins, too. A fake coin is lighter than a genuine coin. How would we find at least one genuine coin using two weighings on a balance scale?
It is conceivable that your two weighings may find more than one genuine coin. The more difficult question that Konstantin and his commentators discuss is the maximum number of genuine coins you can guarantee to identify in two weighings. Konstantin and the others propose 14 as the answer, but do not have a proof yet.
I wonder if one of you can find a bigger number than Konstantin or alternatively a proof that indeed 14 is the largest possible.
You might ask, considering the title of this piece, why I think that coins are scary. No, I am not afraid of coins. It scares me that this problem was given to eighth graders in Russia, because I cannot imagine that it would be given to kids that age in the USA.
By the way, ten eighth grade students in Russia solved this problem during the competition.
I recently wrote two pieces about the puzzle relating to sons born on a Tuesday: A Son born on Tuesday and Sons and Tuesdays. I also posted a beautiful essay on the subject by Peter Winkler: Conditional Probability and "He Said, She Said". Here is the problem:
You run into an old friend. He has two children, but you do not know what their gender is. He says, "I have a son born on a Tuesday." What is the probability that his second child is also a son?
A side note. My son Alexey explained to me that I made an English mistake in the problem in those previous posts. It is better to say "born on a Tuesday" than "born on Tuesday." I apologize.
Despite this error, I was gratified to hear from a number of people who told me that I had converted them from their solution to my solution. To ensure that the conversion is substantial, I've created a new version of the puzzle on which my readers can test out their new-found understanding. Here it is:
You run into an old friend. He has two children, but you do not know what their gender is. He says, "I have a son born on a Tuesday." What is the probability that his second child is born on a Wednesday?
I was terribly shy when I was a teenager. I worked on this problem and overcame it. But when I moved to the US my shyness returned in a strange form. I was fine around Russians but shy around Americans. At first I assumed that it was a language problem.
I became friends with a Russian sexologist and psychotherapist. He pointed out that I never initiated a conversation with Americans and so I realized that my shyness had returned. He prescribed an exercise for me: I had to invite a new American guy to lunch once a week.
Why guys? Maybe because he was a sexologist or maybe because my problems with self-esteem were more pronounced when I was around men. In any case, I decided to do the exercise.
To paint the full picture I need to add some relevant details. At that time I was married, although I didn't wear a ring, and wasn't especially interested in other men. The reason I didn't wear a ring was that Joseph, my husband at the time, did not himself want to wear a ring. As I love symmetry in relationships more than I love rings, I didn't wear one either.
The men I was about to invite to lunch were mere acquaintances, because I had not yet made any American friends. So although I didn't intend to hide it, they may not have realized that I was married.
Two things surprised me in this exercise. First, it was very easy. Most people agreed to do lunch with me.
Second, every man I invited mentioned his girlfriend. This was unexpected. From my experience with Russians, I anticipated that every man would hide his involvement with someone else, even with a wife, at least for some time. At the very least, many Russian men would try to flirt.
The Americans were different. Unclear why I had invited them out, they wanted to be upfront with me from the start, just in case I was interested in them. Since that experience, I admire the way that American men come clean.
I never invited any of these guys out twice: I just needed a supply of new men for my exercise in overcoming my shyness. I wonder if they thought I was put off by their confessions. Perhaps my loss of interest in them after the first lunch confirmed their suspicions that I was attracted to them.
The sexologist's exercise was a success. Today I have no trouble inviting someone to lunch.

John Conway has a T-shirt with his theorem on it. I couldn't miss this picture opportunity and persuaded John to pose for pictures with his back to me. Here is the theorem:
If you continue the sides of a triangle beyond every vertex at the distances equaling to the length of the opposite side, the resulting six points lie on a circle, which is called Conway's circle.
Poor John Conway had to stand with his back to me until I figured out the proof of the theorem and realized which point must be the center of Conway's circle.
Heard somewhere:
Teacher: What's bigger: 22/7 or 3.14?
Student: They are equal.
Teacher: Why do you say that?!
Student: They are both equal to π.

For the last three years I've been coming to the Institute for Advanced Study in Princeton every spring for the Women and Mathematics program. Every year I am assigned to an office in the main building: Fuld Hall.
The problem is that there is a different office that I crave. Every year I go and check on it over in Simonyi Hall, where the Mathematics Department is located. This year I took this photo of the empty name-tag, hoping that one day it will say Tanya Khovanova.
Credit cards often keep your mother's maiden name in their database for security purposes. This so called "security" is based on two assumptions:
Were these assumptions true, only your close relatives would know your mother's maiden name. In reality, if your mother was never married, then your last name is the same as your mother's last name. So, crooks who are trying to steal identities can try to use your last name as your mother's presumed maiden name. Very often they will succeed. Besides, many women do not change their last names. If you have a different last name from your mother, but your mother uses her maiden name, then the bank's security question is not very secure at all.
If you want your identity to be secure you might need to invent a maiden name for your mother. Alternatively, perhaps your parents can tell you a family secret that will help you choose a name that is related to you, but not transparent to the public.
My relative Martin took his wife's last name after their marriage. Before his children apply for credits cards and bank accounts, he needs to explain to them that it is better for them to use his maiden name as their mother's maiden name for banking purposes.
I was driving on MassPike when, for no apparent reason, a car driving in the opposite direction started flashing its headlights. I remembered the Russian tradition of informing the oncoming traffic that the police are nearby. So I adjusted my speed and very soon I saw a police car. I got this warm feeling in my heart because I didn't need to panic or check my speedometer. I mentally thanked that anonymous Russian driver and started wondering why the tradition had not been adopted in the USA. Is it because we are so responsible that we want to punish speeders, or do we think that the police are on our side?
The following problem was sent to me by Joel Lewis.
You have 12 mice, one of which eats faster than all the others. You need to find it. You have a supply of standard cupcakes that you value very much and want to minimize how many of them you have to use. The only way you can find the mouse is to give cupcakes to several groups of mice and see which group is the fastest.
We assume that mice chew at a constant speed and all the mice in one group can attack the cake at the same time. I love this puzzle because I love coin problems. Let me restate the puzzle as a coin problem:
You have 12 coins, one of which is fake and weighs less than all the others. You have a balance scale with multiple pans, that is you can weigh several things at once and order them by weight. You do not care about the total number of weighings as in most classical coin puzzles, instead, this time using a pan is expensive and you want to find the fake coin with as few pan-uses as possible.
Spoiler warning: below I will discuss the solution for n mice.
You can, of course, give a cake to every mouse and see which one finishes first. You can save one cake by giving cakes at the same time to all but one of the mice. If everyone finishes simultaneously, the faster mouse is the unfed one.
It wastes cakes to give them to unequally-sized groups of mice. We can do better by copying the classical way to find a fake coin with the minimum number of weighings. That is, for each test, divide the mice into three groups as evenly as possible and give a cake to each of two equally-sized groups. The number of cakes you use is about 2log3n.
I wouldn't have written this essay if that was the solution. Sometimes you can do even better. For example, you can find the faster mouse out of 12 using only 5 cakes.
First, if you give out k cakes in one test, the test tells you which of k+1 groups the mouse is in. In the worst case, the faster mouse will be in the biggest group, so you should minimize the biggest group. Hence, your groups that get cakes should have ⌈n/(k+1)⌉ mice.
A test with one cake gives no information. I argue that giving out more than three cakes doesn't gain anything. Indeed, suppose we use four cakes in a test. That is, we divide the mice into five groups A, B, C, D and E, of which the first four are the same size. We can simulate the test by two tests in each of which we give out two cakes. In the first test we give cakes to A+B and C+D. If one of the groups is faster, say A+B, then in the second test give cakes to A and B; if not, E has the faster mouse. I leave it as an exercise to simulate a test with more than four cakes.
Thus, in an optimal strategy we can use two or three cakes per test. Also, if you give one test with k − 1 cakes and the next one with m − 1 cakes, you can switch them with the same effect. The largest group after either order of tests will have at most ⌈n/km⌉ mice.
I don't need two tests of three cakes each, which would give me a group of size at least ⌈n/16⌉. I can achieve the same result with three tests of two cakes each, with the faster mouse restricted to a group of size at most ⌈n/27⌉.
That means all my tests use two cakes, except I might use three cakes once. It doesn't matter in what order I conduct the tests, so I can wait until the end to use three cakes. I leave it as an exercise to the reader that the only small number of mice for which we would prefer three cakes is four. From this it follows quickly that for numbers of mice between 3 * 3i + 1 and 4 * 3i, the number of cakes is 2i + 1. For numbers between 4 * 3i + 1 and 3i+2 the answer is 2i + 2.
A week ago I chatted with my son Sergei about memorable math problems. He mentioned problem 5 from USAMO 2007. The problem can be reduced to the following:
Prove that (x7 + 1)/(x + 1) is composite for x = 77n, where n is a non-negative integer.
Perhaps Sergei remembered this problem because as far as he knew, he was the only one in that competition to solve it. That made me curious as to how he solved it. His solution is available as solution 2 at the Art of Problem Solving website. His solution seemed mysterious and impossible to invent on the spot. I became even more curious to understand the thought process underlying his solution.
Here is his recollection:
We need to factor x6 − x5 + x4 − x3 + x2 − x + 1. If such factoring existed it would have been known. Therefore, we need to somehow use the fact that x = 77n. What is the simplest way to factor? We should try to represent the polynomial in question as the difference of squares. Luckily, x is an odd power of 7. We can make it a square if we multiply or divide it by 7 or another odd power of 7. So with a supply of squares on one side, we need to find a match for one of them to build the difference.
Let us simplify the problem and see what happens for (y3 + 1)/(y + 1) for y = 33n, when n = 1. In other words we want to represent 703 as a difference of squares. This can be done: 703 = 282 − 92. Now let us see how we can express 282 and 92 through y which in this case is equal to 27. The first term is (y + 1)2, and the second is 3y.
Now let's go back to 7 and x, and check whether (x + 1)6 − (x6 − x5 + x4 − x3 + x2 − x + 1) is 7x. Oops, no. The difference is 7x5 + 14x4 + 21x3 + 14x2 +7x. On the plus side, it is divisible by 7x which we know is a square. The leftover factor is x4 + 2x3 + 3x2 +2x + 1, which is a square of x2 +x + 1.
The problem is solved, but the mystery remains. The problem can't be generalized to numbers other than 3 and 7.
I decided to take a closer look at the Putnam Competition. I analyzed the results of the three top contenders for the best Putnam teams: Harvard, MIT, Princeton. I looked at the annual number of Putnam Fellows from each of these three schools starting from 1994.
| Year | Harvard | MIT | Princeton |
|---|---|---|---|
| 1994 | 2 | 0 | 1 |
| 1995 | 3 | 0 | 0 |
| 1996 | 2 | 0 | 0 |
| 1997 | 4 | 0 | 0 |
| 1998 | 2 | 0 | 1 |
| 1999 | 2 | 1 | 0 |
| 2000 | 2 | 2 | 0 |
| 2001 | 2 | 1 | 0 |
| 2002 | 2 | 2 | 0 |
| 2003 | 1 | 2 | 1 |
| 2004 | 0 | 3 | 2 |
| 2005 | 2 | 3 | 1 |
| 2006 | 1 | 3 | 0 |
| 2007 | 1 | 2 | 1 |
| 2008 | 1 | 3 | 0 |
| 2009 | 1 | 2 | 0 |
As you may notice MIT couldn't even generate a Putnam Fellow until 2000, but starting from 2003 MIT consistently had more Putnam Fellows than Harvard or Princeton.
Richard Stanley, the coach of the MIT team, kindly sent me the statistics for the most recent competition, held in 2009.
| Category | Overall | MIT |
|---|---|---|
| Number of participants | 4036 | 116 |
| Mean score | 9.5 | 34.7 |
| Median score | 2 | 31 |
| Geometric mean | 0 | 0 |
| Percent of 0 score | 43.7 | 4.3 |
Furthermore, MIT had 40% in the top 5, 33% in the top 15, 32% in the top 25, and 35% in the top 81. For comparison, in the top 81, MIT had 28 winners — more than the next three schools together: Caltech 11, Harvard 9, Princeton 7.
No comment.
OnlineDegree.net selected the 50 Best Blogs for Math Majors, and I am pleased that Tanya Khovanova's Math Blog is number two. Since they did not explain their criteria, I suspected that it might be according to the number of Google hits. To double check, I Googled "math blog" and once again my blog was number two.
This might be the right moment to acknowledge the others involved with my blog. First, Sue Katz, my writing teacher and editor, corrected the English in most of my posts. Now I do not "do" mistakes in English any more, I make them.
My sons, Alexey and Sergei, are a huge support. Sometimes my poor kids have to listen endlessly to my latest idea, until I am ready to write about it. And then they will even read the final piece, and continue to encourage me.
But the most important motivators are you, my readers. Your comments, your personal emails and your feedback keep me writing.

I am usually disappointed with American math text books. I have had an underwhelming experience with them. Often I open a book and in the next 15 minutes, I find a mistake, a typo, a misguided explanation, sloppiness, a misconception or some other annoyance.
I was pleasantly surprised when I opened the book Introduction to Algebra by Richard Rusczyk. I didn't find any flaws in it — not in the first 15 minutes, and not even in the first hour. In fact, having used the book many times I have never found any mistakes. Not even a typo. This was disturbing. Is Richard Rusczyk human? It was such an unusual experience with an American math book, that I decided to deliberately look for a typo or a mistake. After half a year of light usage, I finally found something.
Look at problem 7.3.1.
Five chickens can lay 10 eggs in 20 days. How long does it take 18 chickens to lay 100 eggs?
There is nothing wrong with this problem. But the book is accompanied by the Introduction to Algebra Solutions Manual in which I found the following solution, that I've shortened for you:
The number of eggs is jointly proportional to the number of chickens and the amount of time. One chicken lays one egg in 10 days. Hence, 18 chickens will lay 100 eggs in 1000/18 days, which is slightly more than 55 and a half days.
What is wrong with this solution? Richard Rusczyk is human after all.
I like this book for its amazing accuracy and clean explanations. There are also a lot of diverse problems in terms of difficulty and ideas. Richard Rusczyk has good taste. Many of the problems are from different competitions and require inventiveness. I like that there are a lot of challenge problems that go beyond the boring parts of algebra. Also, I like that important points of algebra are chosen wisely and are emphasized.
This book might not be for everyone. It doesn't have pretty pictures. It doesn't have color at all. This is not a flaw for a math book. The book concentrates on ideas and problems, not entertainment. So if you're looking for math entertainment, you'll find it on my blog. For solid study, try Richard Rusczyk's books.

I love Raymond Smullyan's books , especially the trick puzzles he includes. The first time I met him in person, he played a trick on me.
This happened at the Gathering for Gardner 8. We were introduced and then later that day, the conference participants were treated to a dinner event that included a magic show. In one evening I saw more close-up magic tricks than I had in my whole life. This left me lightheaded, doubting physics and my whole scientific outlook on life.
Afterwards, Raymond Smullyan joined me in the elevator. "Do you want to see a magic trick?" he asked. "I bet I can kiss you without touching you." I was caught off guard. At that moment I believed anything was possible. I agreed to the bet.
He asked me to close my eyes, kissed me on the cheek and laughed, "I lost."
As a writer of books on mathematical puzzles I am often faced with delicate issues of phrasing, none more so than when it comes to questions about conditional probability. Consider the classic "X has two children and at least one is a boy. What is the probability that the other is a boy?"
It is reasonable to interpret this puzzle as asking you "What is the probability that X has two boys, given that at least one of the children is a boy" in which case the answer is unambiguously 1/3—given the usual assumptions about no twins and equal gender frequency.
This puzzle confounds people *legitimately*, however, because most of the ways in which you are likely to find out that X has at least one boy contain an implicit bias which changes the answer. For example, if you happen to meet one of X's children and it's a boy, the answer changes to 1/2.
Suppose the puzzle is phrased this way: X says "I have two children and at least one is a boy." What is the probability that the other is a boy?
Put this way, the puzzle is highly ambiguous. Computer scientists, cryptologists and others who must deal carefully with message-passing know that what counts is not what a person says (even if she is known never to lie) but *under what circumstances would she have said it.*
Here, there is no context and thus no way to know what prompted X to make this statement. Could he instead have said "At least one is a girl"? Could he have said "Both are boys"? Could he have said nothing? If you, the one faced with solving the puzzle, are desperate to disambiguate it, you'd probably have to assume that what really happened was: X (for some reason unconnected with X's identity) was asked whether it was the case that he had at least one son, and, after being warned—by a judge?—that he had to give a yes-or-no answer, said "yes." An unlikely scenario, to say the least, but necessary if you want to claim that the solution to the puzzle is 1/3.
Consider the puzzle presented (according to Alex Bellos) by Gary Foshee at the recent 9th Gathering for Gardner:
I have two children. One is a boy born on a Tuesday. What is the probability I have two boys?
If the puzzle was indeed put exactly this way, and your life depended on defending any particular answer, God help you. You cannot answer without knowing, for example, what the speaker would have said if he had one boy and one girl, and the boy was born on Wednesday. Or if he had two boys, one born on Tuesday and one on Wednesday. Or two girls, both born on Tuesday. Et cetera.
Now, there is nothing mathematically wrong (given the usual assumptions, including X being random) about saying that "The probability that X has two sons, given that at least one of X's two children is a boy born on Tuesday, is 13/27." But if that is to be turned into an unambiguous puzzle attached to a presumed situation, some serious hypothesizing is necessary. For instance: you get on the phone and start calling random people. Each is asked if he or she has two children. If so, is it the case that at least one is a boy born on a Tuesday? And if the answer is again yes, are the children both boys? Theoretically, of the times you reach the third question, the fraction of pollees who say "yes" should tend to 13/27.
Kind of takes the fun out of the puzzle, though, doesn't it? Kudos to Gary for stirring up controversy with a quickie.
I recently discussed the following problem:
You run into an old friend. He has two children, but you do not know their genders. He says, "I have a son born on Tuesday." What is the probability that his second child is also a son?
I had heard this problem at the Gathering for Gardner 9 in a private conversation. My adversary had been convinced that the answer to the problem is 13/27. I came back to Boston from the gathering and wrote my aforementioned essay in which I disagreed with his conclusion.
I will tell you my little secret: when I started writing I substituted Wednesday for Tuesday. Then I checked my sons' birthdays and they were born on Saturday and Tuesday. So I changed my essay back to Tuesday.
After I published it people sent me several links to other articles discussing the same problem, such as those of Keith Devlin and Alex Bellos, both of whom think the answer is 13/27. So I invented a fictional opponent — Jack, and here is my imaginary conversation with him.
Jack: The probability that a father with two sons has a son born on Tuesday is 13/49. The probability that a father with a son and a daughter has a son born on Tuesday is 1/7. A dad with a son and a daughter is encountered twice as often as a dad with just two sons. Hence, we compare 13/49 with 14/49, and the probability of the father having a second son is 13/27.
Me: What if the problem is about Wednesday?
Jack: It doesn't matter. The particular day in question was random. The answer should be the same: 13/27.
Me: Suppose the father says, "I have a son born on *day." He mumbles the day, so you do not hear it exactly.
Jack: Well, as the answer is the same for any day, it shouldn't matter. The probability that his second child will also be a son is still 13/27.
Me: Suppose he says, "I have a son born …". So he might have continued and mentioned the day, he might not have. What is the probability?
Jack: We already decided that it doesn't depend on the day, so it shouldn't matter. The probability is still 13/27.
Me: Suppose he says, "I have a son and I do not remember when he was born." Isn't that the same as just saying, "I have a son." And by your arguments the probability that his second child is also a son is 13/27.
Jack: Hmm.
Me: Do you remember your calculation? If we denote the number of days in a week as d, then the probability of him having a second son is (2d−1)/(4d−1). My point is that this probability depends on the number of days of the week. So, if tomorrow we change a week length to another number his probability of having a son changes. Right?
At this point my imaginary conversation stops and I do not know whether I have convinced Jack or not.
Now let me give you another probability problem, where the answer is 13/27:
You pick a random father of two children and ask him, "Yes or no, do you have a son born on Tuesday?" Let's make a leap and assume that all fathers know the day of the births of their children and that they answer truthfully. If the answer is yes, what is the probability of the father having two sons?
Jack's argument works perfectly in this case.
My homework for the readers is: Explain the difference between these two problems. Why is the second problem well-defined, while the first one is not?

On March 5, 2010 I visited Princeton and had dinner with John Conway at Tiger Noodles. He gave me the second Doomsday lesson right there on a napkin. I described the first Doomsday lesson earlier, in which John taught me to calculate the days of the week for 2009. Now was the time to expand that lesson to any year.
As you can see on the photo of the napkin, John uses his fingers to make calculations. The thumb represents the DoomsDay Difference, the number of days your birthday is ahead of DoomsDay for a given year. To calculate this number you have to go back to my previous post.
The index finger represents the century adjustment. For example, the Doomsday for the year 1900 is Wednesday. Conway remembers Wednesday as We-are-in-this-day. He invented his algorithm in the twentieth century, not to mention that most people who use his algorithm were born in that century. Conway remembers the Doomsday for the year 2000 as Twosday.
The next three fingers help you to calculate the adjustment for a particular year. Every non-leap year has 52 weeks and one day. So the Doomsday moves one day of the week forward in one year. A leap year has one extra day, so the Doomsday moves forward two days. Thus, every four years the Doomsday moves five days forward, and, consequently, every twelve years it moves forward to the next day of the week. This fact helps us to simplify our year adjustment by replacing every dozen of years with one day in the week.
The middle finger counts the number of dozens in the last two digits of your year. It is important to use "dozen" instead of "12" as later we will sum up all the numerals, and the word "dozen" will remind us that we do not need to include it in the sum.
The ring finger represents the remainder of the last two digits of the year modulo 12, and the pinkie finger represents the number of leap years in that remainder.
John made two sample calculations on the napkin. The first one was for his own birthday — December 26, 1937. John was born exactly on Doomsday. I suspect that that is the real reason he called his algorithm the Doomsday Algorithm. The century adjustment is Wednesday. There are 3 dozens in 37, with the remainder 1 and 0 leap years in the remainder. When we add four more days to Wednesday, we get Sunday. So John Conway was born on Sunday.
The second napkin example was the day we had dinner: March 5, 2010. March 5 is 5 days ahead of the Doomsday. The century adjustment is Twosday, plus 0 dozens, 10 years in the remainder and 2 leap years in the remainder. 5 + 0 + 10 + 2 equals 3 modulo 7. Hence, we add three days to Tuesday, demonstrating that we dined out together on Friday. But then, we already knew that.
Do you know that some Russian letters are shaped exactly as some letters in the English alphabet? The shapes are the same, but the sounds of the letters are not. My Russian last name can be completely spelled using English letters: XOBAHOBA.
The adequate translation of my last name into English is Hovanova. You might ask where the first "K" came from. For many years French was considered the language of diplomacy and the USSR used French as an official language for traveling documents.
But "H" in French is silent and "Hovanova" would have been pronounced as "Ovanova." To prevent that, Russians used "kh" for the "h" sound.
Now to my first name. I was born Tatyana, for which Tanya is a nickname. Back in Russia, Tanya is used for children and students and Tatyana for adults and teachers. As I was a student throughout my 30 years of life in Russia, I was always Tanya. When I moved to the US, I decided to keep using Tanya, which I much preferred to Tatyana.
A psychiatrist might think that I wanted to be a student forever or refused to grow up. Or I could be accused of being lazy, as Tanya is shorter. In reality, I was just trying to be considerate. Tanya is easier to write and to spell for Americans. Anyway, I already had enough problems spelling out my last name in this country.
Now that more information is getting translated from Russian into English, I keep stumbling on references to me as to Hovanova or Tatyana. For example, the IMO official website used Russian sources to come up with the names of the Russian participants. They then translated the names directly into English, instead of going through French. As a result, on their website I am Tatyana Hovanova. This is not unique to me: many Russian names on the IMO website differ from those peoples' passport names.
By the way, if you Google my last name you will encounter other Khovanovas. Khovanova is not a particularly unusual name. Only one of the Khovanovas that came up in my search results is a close relative. Elizabeth Khovanova is my father's second wife and a dear friend. She is also an accomplished geneticist.
Khovanova is used only for females in Russia. The male equivalent is Khovanov. Surely you have heard of my half-brother Mikhail Khovanov and his homologies.
I gave you the Wise Men Without Hats puzzle in one of my previous posts:
A sultan decides to check how wise his two wise men are. The sultan chooses a cell on a chessboard and shows it to the first wise man. In addition, each cell on the chessboard either contains a pebble or is empty. The first wise man has to decide whether to remove one pebble or to add one pebble to an empty cell. Next, the second wise man must look at the board and guess which cell was chosen by the sultan. The two wise men are permitted to agree on their strategy beforehand. What strategy can they find to ensure that the second wise man will always guess the chosen cell?
My readers solved it. The solution is the following. Let us assign a number between 0 and 63 to every cell of the board. The second wise man takes numbers corresponding to cells with pebbles, converts them to binary and XORs the result. The answer is the cell number that he is seeking. The first wise man can always add or remove a pebble to make the XORing operation of the remaining pebbles produce any given number from 0 to 63.
This solution only works for boards that have a power of two as the number of cells.
Let's look at the solution more closely. Let us create a graph corresponding to this problem. The vertices of the graph will correspond to the positions of pebbles. That means vertices are in one-to-one correspondence with the subsets of the set of 64 elements. Let us connect two vertices if we can get from one position to another by removing or adding a pebble. That means vertices are connected if two corresponding sets differ by exactly one element. We can see that the resulting graph is regular and each vertex is connected to exactly 64 other vertices.
Let us assign one out of 64 colors to each cell of the chessboard. The second wise man can guess the cell by looking at the chessboard. From this we can conclude that there is a bijection from the vertices of the graph to chessboard cells. In other words, we can color the graph in 64 colors. The existence of the strategy for wise men means that we can color the graph in such a way that each vertex is connected to the vertices of all colors.
As each vertex in our graph has exactly 64 neighbors, the graph has the following property: It can be colored in 64 colors in such a way that every vertex is connected to exactly one vertex of every color.
As soon as I realized that there is such a graph-theoretical object, I started to run around MIT asking everyone if such objects were studied or have a name.
It appears that indeed such an object has a name. A graph that can be colored into k colors in such a way that every vertex has exactly one neighbor of every color is called a rainbow graph.
Andrew Woldar discusses properties of such graphs in his paper. In particular, rainbow graphs are matching graphs. Indeed, every vertex is connected to exactly one vertex of the same color. Hence there is a natural pairing on vertices. From here, we can conclude that the smallest size of a rainbow graph is 2k.
Several MIT students liked the wise men problem and the associated graph object so much that they decided to study them. Hwanchul Yoo, SuHo Oh, and Taedong Yun enumerated all rainbow graphs of size 2k. The number of non-isomorphic rainbow graphs of size 2k equals mitthe number of switching classes of graphs with k vertices. The corresponding sequence A002854 starts as: 1, 1, 2, 3, 7, 16, 54. The paper is soon to appear. It is titled "Rainbow Graphs and Switching Classes."
Just received from Victor Gutenmacher:
Fibonacci salad: For today's salad, mix yesterday's leftover salad with that of the day before.
New additions to my trick problems collection:
* * *
It takes 12 minutes to saw a log into 3 parts. How much time will it take to saw it into 4 parts?
* * *
The Davidsons have five sons. Each son has one sister. How many children are there in the family?
* * *
A caterpillar wants to see the world and decides to climb a 12-meter pole. It starts every morning and climbs 4 meters in half a day. Then it falls asleep for the second half of the day during which it slips 3 meters down. How much time will it take the caterpillar to reach the top?
First Name: David
Last Name: (hidden for privacy protection)
Year of Birth: (hidden for privacy protection)
email: buchanan1985@gmail.com
I remember a math problem from my childhood: divide an L-shaped triomino into four congruent parts. The answer is in the picture on the left. Such division is quite appropriately called a reptile (repetitive tiling). Solomon Golomb invented the name many years ago. He wasn't aware that his definition would end up creating Googling problems, for when you search for such a mathematical object you will stumble upon a lot of amphibians.
Similarly, you can divide the same shape into 9 congruent pieces (see the figure on the left).
Suppose you want to divide a shape into pieces that are similar, but not necessarily of the same size. Such tiling is called an irreptile (irregular reptile).

At the Gathering for Gardner 9 I listened to Carolyn Yackel's talk about the L-reptiles and L-irreptiles. One of the ways to create an irreptile is to start with a reptile, then to make a sub-tiling of one of the existing tiles. This procedure can be repeated many times.
Carolyn brought a ceramic table to the Gathering for Gardner. This table is made of two L-shapes. Both shapes are irreptiles, created by this procedure. In one part of the table she started with a 9-reptile, and in the other with a 4-reptile. She sent me this picture of her table to use in this essay.
After her talk I started wondering how many tiles can an L-irreptile be comprised of. We start with one piece: the L-shape itself. If we divide a tile into four smaller tiles we add three more pieces. If we divide it into nine tiles we add eight more pieces. We can mix sub-dividing into four and nine tiles. The total number of tiles that an L-shape can be comprised of by this procedure is all the numbers you can get from 1 by adding three or eight. The sequence is 1, 4, 7, 9, 10, 12, 13, 15, 16, 17 and so on. Starting from 15 we get all the consecutive numbers.
The numbers that are not represented in the above sequence are 2, 3, 5, 6, 8, 11 and 14. Can we divide an L-shape into such numbers of tiles? Benoît Jubin reminded me that there is an L-reptile with six pieces.
Consequently, we can add 5 more pieces to any L-irreptile. Thus, there exists an L-irreptile made out of 11 (1+5+5) and out of 14 (1+8+5) pieces. The numbers that are left are 2, 3, 5 and 8.
While I was discussing L-irreptiles with fans of sequences, David Wilson suggested a conjecture.
David Wilson's conjecture. If there is an L-irreptile, there is a corresponding square-irreptile with similarly-sized pieces.
If this conjecture is true, then we can see that L-irreptiles with 2, 3 or 5 pieces can't exist as corresponding square-irreptiles do not exist.
For example, to prove that 2 or 3 square-irreptiles can't exist, you need to notice that each corner of the square we are trying to tile should belong to a different small tile.
The question of the existence of an 8-irreptile of the L-shape is more interesting and challenging. The square 8-irreptile exists. If you can prove that the L-shape 8-irreptile doesn't exist, then you will automatically prove that the converse to Wilson's conjecture is not true.

Only at MIT. Room 4-231.
Let n coins weighing 1, 2, … n be given. Baron Münchhausen knows which coin weighs how much, but his audience does not. Define a(n) to be the minimum number of weighings the Baron must conduct on a balance scale, so as to unequivocally demonstrate the weight of at least one of the coins.
In the paper Baron Münchhausen's Sequence, three of us completely described the Baron's sequence. In particular, we proved that a(n) ≤ 2. Here we would like to outline another proof idea, which is interesting in part because it touches the Riemann hypothesis.
We denote the total weight of coins in some set A as |A|.
Lemma. Numbers n that can be represented as Ti + Tj + Tk = 3n, where i ≤ j < k, such that there is a subset A of coins from j + 1 to k such that n = Tj + |A|, can be done in two weighings.
Proof. Suppose Ti + Tj + Tk = 3n and there is a subset A of coins from j + 1 to k such that n = Tj + |A|. We propose the two weighings
[1…j] + A = n
and
[1…i] + B = n + A,
where B is the complement of A in {j + 1, j + 2, … , k}.
If we sum up twice the first weighing with the second weighing we get
3[1…i] + 2[(i + 1)…j] + 2A + B = 3n + A.
In other words, three times the weight of the coins that were on the left side in both weighings, plus twice the weight of the coins that were on the left side in only the first weighing, plus the weight of the coins that were moved from the left cup to the right cup plus the weight of the coins on the left cup in only the second weighing equals three times the weight of the coin on the right cup in both weighings. Hence three times the weight of the coin on the right cup in both weighings can't be less than the weight of the k other coins that participated plus the weight of the j coins that were on the left cup in the first weighing and weren't moved to the right cup, plus the weight of the i coins that were one the left cup in both the first and the second weighing. But because Ti + Tj + Tk = 3n, then 3n is the smallest possible weight of any set of i plus j plus k coins, the coin on the right cup in both weighings has to be the n-coin.
We checked that any number up to 600,000 except 20 can be represented so as to satisfy the Lemma. To show how to solve 20 coins in two weighings is easy, and, as usual, is left as an exercise for the reader. Next, we want to look at the following lemma.
Lemma. Given a set of consecutive numbers {(j + 1), … , k}, if k > 2j + 2, then it is possible to find a subset in the set that sums up to any number in the range from j + 1 to (j + k + 1)(k – j)/2 – j – 1.
We won't prove the lemma, but it means that if k is about twice larger than j, then we have a lot of flexibility for building our set A in the weighing above. For moderately large n (where 600000 >> "moderately large"), it is not hard to prove that this flexibility is sufficient.
Now the question becomes: can we find such a decomposition into triangular numbers? It is enough to find a representation Ti + Tj + Tk = 3n, where Tk is at least 81% of 3n.
We know that decompositions into triangular numbers are associated with decompositions into squares. Namely, if Ti + Tj + Tk = 3n, then (2i + 1)2 + (2j + 1)2 + (2k + 1)2 = 24n + 3. If the largest square is at least 81% of 24n + 3, then the largest triangular number in the decomposition of 3n is at least 81%.
There is a theorem (W. Duke, Hyperbolic distribution problems and half-integral weight Maass forms, in Inventiones Math 92 (1988) p.73-90) that states that in the limit the decompositions of numbers into three squares are equidistributed. That is, if we take some region on the unit sphere x2 + y2 + z2 = 1 (for example, the region |z| > 0.8) and view decompositions of 24n + 3 into squares as points on the sphere x2 + y2 + z2 = 24n + 3, then, as n grows, decompositions whose projections fall into our chosen region are guaranteed to appear.
This theorem is great, because it tells us that for large enough n we will always be able to find a decomposition of 24n + 3 into triangle numbers where one of the triangle numbers will be much bigger than the others, and it will be possible to prove the weight of the n coin in two weighings. Unfortunately, this summary, as stated, does not tell us how large that n needs to be. So we need some exact estimates.
The number of decompositions of m into sums of three squares is about the square root of m. More precisely, it is possible to compute a number N, such that for any number m > N, with at most one exception, the number of decompositions is at least Cm1/2−1/30, where C is a known constant.
The more specific statement of Duke's theorem is that if the number of solutions to the quadratic x2 + y2 + z2 = 24n + 3 is large, for a computable value of "large", then the solutions are equidistributed. More precisely, let us denote 3n by m and fix an area Ω on the unit sphere. Then the number of solutions (x, y, z) such that the unit vector (x, y, z)/|(x, y, z)| belongs to Ω is
1/(4π) Ωh(8m+3) + E(m),
where h(8m+3) is the total number of solutions of x2 + y2 + z2 = 24n + 3, and E(m) is an error term, which starting from some number satisfies the inequality: E(m) ≤ 1000m1/2-1/7.
That's pretty good, because combining these two lets us, at least in principle, actually calculate an N such that for all n > N except maybe one a(n) = 2. After that we hoped to write a program to exhaustively search smaller numbers by computer.
This situation is still somewhat annoying, because that possible exception must then be propagated into the proof, and if we are not careful, possibly into the final theorem. ("No matter how many coins the Baron has, he can prove the weight of one in at most two weighings, except maybe one number of coins, and we don't know which...") This is where the Riemann Hypothesis comes in. If the Riemann Hypothesis is true, then that exception isn't there, and all is sunlight and flowers.
The beauty of the Baron's puzzle is such that we actually do not need the Riemann hypothesis. As we can use unbalanced weighings, it is enough to find a good decomposition for one out of the four numbers 3n, 3n-1, 3n-2, or 3n-3.
Instead of finding all these exact estimates we found a different elementary proof of our theorem. But we are excited that methods that are used in very advanced number theory can be used to solve a simple math problem that can be described to middle school children.
It would be great if someone decided to finish this proof.

I am used to thinking that a "woman in numbers" means a female number theorist. But not anymore. I just discovered drawings by Svetlana Bogatyr. From now on the expression a "woman in numbers" will convey an additional meaning to me.
I am grateful to Svetlana for permitting me to post several of her drawings. The "Mature Woman" is on the left. "Eurydice", "Girl in Scarf" and "Holland Woman " are below.
Enjoy.



I just invented a two-player game. To start, you have an empty n by n board. When it's your turn you must write an integer between 1 and n into an empty cell on the board. Your integer has to differ from the integers that are already present in the same row or column. If you finish filling up the board, you will get a Latin square and the game will be a tie. The person who doesn't have a move loses. What is the best strategy?
Let's see what happens if n is 2. The first player puts any number in one of the four corners of the 2 by 2 board. The second player wins by placing a different number in the opposite corner.
I played this game with my son Sergei Bernstein on a 3 by 3 board. We discovered that the first player can always win. Since this game is so much fun, I'll leave it to the reader to play it and to find the winning strategy for the first player.
Can you analyze bigger boards? Remember that this game has many symmetries. You can permute rows and columns. Also, you can permute numbers.
While we were playing Sergei invented two theorems.
Sergei's theorem 1. If n is odd the first player can guarantee a tie.
Proof. In the first move the first player writes (n+1)/2 in the center cell. If the second player puts number x in any cell the first player puts number n+1−x into the cell that is rotationally symmetric to the second player's cell with respect to the center. With this strategy the first player will always have a legal move.
Sergei's theorem 2. If n is even the second player can guarantee a tie.
Proof. If the first player puts number x in any cell the second player puts number n+1−x into the cell that is vertically symmetric to the first player's cell with respect to the vertical line of symmetry of the board. With this strategy the second player will always have a legal move.
As you play the game, let me know if you develop any theorems of your own.
Suppose you meet a friend who you know for sure has two children, and he says: "I have a son born on Tuesday." What is the probability that the second child of this man is also a son?
People argue about this problem a lot. Although I've discussed similar problems in the past, this particular problem has several interesting twists. See if you can identify them.
First, let us agree on some basic assumptions:
Now let us consider the first scenario. A father of two children is picked at random. He is instructed to choose a child by flipping a coin. Then he has to provide information about the chosen child in the following format: "I have a son/daughter born on Mon/Tues/Wed/Thurs/Fri/Sat/Sun." If his statement is, "I have a son born on Tuesday," what is the probability that the second child is also a son?
The probability that a father of two daughters will make such a statement is zero. The probability that a father of differently-gendered children will produce such a statement is 1/14. Indeed, with a probability of 1/2 the son is chosen over the daughter and with a probability of 1/7 Tuesday is the birthday.
The probability that a father of two sons will make this statement is 1/7. Among the fathers with two children, there are twice as many who have a son and a daughter than fathers who have two sons. Plugging these numbers into the formula for calculating the conditional probability will give us a probability of 1/2 for the second child to also be a son.
Now let us consider the second scenario. A father of two children is picked at random. If he has two daughters he is sent home and another one picked at random until a father is found who has at least one son. If he has one son, he is instructed to provide information on his son's day of birth. If he has two sons, he has to choose one at random. His statement will be, "I have a son born on Mon/Tues/Wed/Thurs/Fri/Sat/Sun." If his statement is, "I have a son born on Tuesday," what is the probability that the second child is also a son?
The probability that a father of differently-gendered children will produce such a statement is 1/7. If he has two sons, the probability will likewise be 1/7. Among the fathers with two children, twice as many have a son and a daughter as have two sons. Plugging these numbers into the formula for calculating the conditional probability gives us a probability of 1/3 for the second child to also be a son.
Now let us consider the third scenario. A father of two children is picked at random. If he doesn't have a son who is born on Tuesday, he is sent home and another is picked at random until one who has a son that was born on Tuesday is found. He is instructed to tell you, "I have a son born on Tuesday." What is the probability that the second child is also a son?
The probability that a father of two daughters will have a son born on Tuesday is zero. The probability that a father of differently-gendered children will have a son who is born on Tuesday is 1/7. The probability that a father of two sons will have a son born on Tuesday is 13/49. Among the fathers with two children, twice as many have a son and a daughter than two sons. Plugging these numbers into the formula for calculating the conditional probability will give us a probability of 13/27 for the second child to also be a son.
Now let's go back to the original problem. Suppose you meet your friend who you know has two children and he tells you, "I have a son born on Tuesday." What is the probability that the second child is also a son?
What puzzles me is that I've never run into a similar problem about daughters or mothers. I've discussed this math problem about these probabilities with many people many times. But I keep stumbling upon men who passionately defend their wrong solution. When I dig into why their solution is wrong, it appears that they implicitly assume that if a man has a daughter and a son, he won't bother talking about his daughter's birthday at all.
I've seen this so often that I wonder if this is a mathematical mistake or a reflection of their bias.
How to solve the original problem? The problem is under-defined. The solution depends on the reason the father only mentions one child, or the Tuesday.
The funny part of this story is that I, Tanya Khovanova, have two children. And the following statement is true: "I have a son born on Tuesday." What is the probability that my second child is a son?
How many different months' lengths are possible?
For "simplicity" let's stick to the Gregorian calendar.
Lennart Green is an amazing magician who performs card tricks. He is so good that the judges at the competition of the International Federation of Magic Societies didn't believe his tricks. They assumed that he used the help of stooges, and unfairly disqualified him. At the next competition he used a judge to assist him and won first place in the cards category.
I saw his performance twice. Both times he brought a woman to the stage, but each time it was a different woman. It was clear that he talked to each woman before the performance, presumably asking her permission. Furthermore, during his performances, both of the women looked slightly bored, implying that it might be not their first time. My first impression was that the women were a part of the act. I was fooled just as the judges had been fooled.
What can I say? Lennart Green isn't skilled at picking up the right women. Watch his performance at TED, and remember that he proved that the assistants were clueless.
When the Abel Prize was announced in 2001, I got very excited and started wondering who would be the first person to get it. I asked my friends and colleagues who they thought was the greatest mathematician alive. I got the same answer from every person I asked: Alexander Grothendieck. Well, Alexander Grothendieck is not the easiest kind of person to give a prize to, since he rejected the mathematical community and lives in seclusion.
Years later I told this story to my friend Ingrid Daubechies. She pointed out to me that my spontaneous poll was extremely biased. Indeed, I was asking only Russian mathematicians living abroad who belonged to "Gelfand's school." Even so, the unanimity of those responses continues to amaze me.
Now several years have passed and it does not seem that Alexander Grothendieck will be awarded the Prize. Sadly, my advisor Israel Gelfand died without getting the Prize either. I am sure I am biased with respect to Gelfand. He was extremely famous in Soviet Russia, although less well-known outside, which may have affected the decision of the Abel's committee.
I decided to assign some non-subjective numbers to the fame of Gelfand and Grothendieck. On Pi Day, March 14, 2010, I checked the number of Google hits for these two men. All the Google hits in the rest of this essay were obtained on the same day, using only the full names inside quotation marks.
Google hits do not give us a scientific measurement. If the name is very common, the results will be inflated because they will include hits on other people. On the other hand, if a person has different spellings of their name, the results may be diminished. Also, people who worked in countries with a different alphabet are at a big disadvantage. I tried the Google hits for the complete Russian spelling of Gelfand: "Израиль Моисеевич Гельфанд" and got an impressive 137,000.
Now I want to compare these numbers to the Abel Prize winners' hits. Here we have another problem. As soon as a person gets a prize, s/he becomes more famous and the number of hits increases. It would be interesting to collect the hits before the prize winner is announced and then to compare that number to the results after the prize announcement and see how much it increases. For this endeavor, the researcher needs to know who the winner is in advance or to collect the data for all the likely candidates.
John Thompson is way beyond everyone else's range because he shares his name with a famous basketball coach. But my point is that Gelfand and Grothendieck could have been perfect additions to this list.

I have this fun book at home written by Clifford Pickover and titled Wonders of Numbers: Adventures in Mathematics, Mind, and Meaning. It was published before the first Abel Prize was awarded. Chapter 38 of this book is called "A Ranking of the 10 Most Influential Mathematicians Alive Today." The chapter is based on surveys and interviews with mathematicians.
The most puzzling thing about this list is that there is no overlap with the Abel Prize winners. Here is the list with the corresponding Google hits.
Since there are other great mathematicians with a lot of hits, I started trying random names. In the list below, I didn't include mathematicians who had someone else appear on the first results page of my search. For example, there exists a film director named Richard Stanley. So here are my relatively "clean" results.
If prizes were awarded by hits, even when the search is polluted by other people with the same name, then the first five to receive them would have been:
If we had included other languages, then Gelfand might have made the top five with his 48,000 English-language hits plus 137,000 Russian hits.
This may not be the most scientific way to select the greatest living mathematician. That's why I'm asking you to tell me, in the comments section, who you would vote for.
I got this problem from my friend, a middle-school math teacher, Tatyana Finkelstein.
We have N coins that look identical, but we know that exactly one of them is fake. The genuine coins all weight the same. The fake coin is either lighter or heavier than a real coin. We also have a balance scale.
Unlike in classical math problems where you need to find the fake coin, in this problem your task is to figure out whether the fake coin is heavier or lighter than a real coin. Your challenge is that you are only permitted to use the scale twice. Find all numbers N for which this can be done.
I would like to add an extra twist to the problem above. It is conceivable that there might be several different strategies for finding the direction in which the weight of the fake coin deviates from the real coins. In this case it is better to choose a strategy that can redeem as many coins as possible — that is, to identify the maximum number of coins as real.
The number of coins you identify as real depends on the outcomes of your weighings. Then what is the precise definition of the best strategy?
Let us call a strategy k-redeem if after the weighings you are guaranteed to demonstrate that k coins are real, but you are not guaranteed to demonstrate that k+1 coins are real. Your task is to analyze two-weighing strategies and choose the most profitable one — the strategy that guarantees to redeem the largest possible number of coins, that is, a k-redeem strategy for the largest k.
Sara was born in Boston on February 29, 2008 at 11:00 am. Her parents were quite upset that their calendar-challenged daughter would only be able to celebrate her birthday once in four years. Luckily, science can help Sara's parents. How? Sara can celebrate her birthday every year at the moment when the Earth passes the same point on its orbit around the Sun as when Sara was born.
Assuming that Sara lives her entire life in Boston and that the daylight savings time is not moved earlier into February, your task is to calculate the schedule of Sara's birthday celebrations for 100 years starting from her birth. To simplify your homework, you can approximate one year as 365 days and 6 hours.
Joseph DeVincentis heard my prayers and created an index for MIT mystery hunt puzzles. He created it not because I requested it, but rather because he was on the writing team this year and they needed it. Anyway, finally there is an index.
I have to warn you, though, that this index was created for people who have already solved the puzzles, so the index contains hints for many of the problems and, on rare occasions, solutions.
Now I will do the math index for this year, and I promise that I will avoid big hints.
One fine day in January 2010, John H. Conway shared with me his recipe for success.
1. Work at several problems at a time. If you only work on one problem and get stuck, you might get depressed. It is nice to have an easier back-up problem. The back-up problem will work as an anti-depressant and will allow you to go back to your difficult problem in a better mood. John told me that for him the best approach is to juggle six problems at a time.
2. Pick your problems with specific goals in mind. The problems you work on shouldn't be picked at random. They should balance each other. Here is the list of projects he suggests you have:
3. Enjoy your life. Important problems should never interfere with having fun. When John Conway referred to having fun, I thought that he was only talking about mathematics. On second thought, I'm not so sure.
* * *
Birthdays are beneficial for your health. A new breakthrough statistical study unequivocally proved that the more birthdays one has the longer one lives.
* * *
We know through Erdös that "a mathematician is a device for turning coffee into theorems". It thus follows by duality that a comathematician is a device for turning cotheorems into ffee.
* * *
- What do you do when you see a beautiful girl?
- I download her.
* * *
Programmers wear red T-shirts to match the color of their eyes.
* * *
We invented the decimal system, because humans have ten fingers on their hands; and 32-bit computers, because humans have 32 teeth in their mouths.
* * *
A general shows off a new tank and boasts:
- You see a tank supplied with the most modern computer technology.
- What is the speed of its computer?
- The same as the speed of the tank, of course.
A sultan decides to check how wise his two wise men are. The sultan chooses a cell on a chessboard and shows it to the first wise man. In addition, each cell on the chessboard either contains a rock or is empty. The first wise man has to decide whether to remove one rock or to add one rock to an empty cell. Next, the second wise man must look at the board and guess which cell was chosen by the sultan. The two wise men are permitted to agree on the strategy beforehand. What strategy can they find to ensure that the second wise man will always guess the chosen cell?
If you are stuck, there are many approaches to try. You can attempt to solve the puzzle for a board of size 1 by 2, or for a board of size 1 by 3. Some might find it easier to solve a version in which you are allowed to have a multiple number of rocks on a cell, and the first wise man is permitted to add a rock to a cell that already contains rocks.

This year I am again on the organizing committee of the Women and Mathematics program at Princeton's Institute for Advanced Study. Our subject is "p-adic Langlands Program." It is a fashionable, advanced and very influential program connecting number theory and representation theory.
We invite undergraduate students, graduate students and post-docs to apply. In 2009-2010 the Institute has been running a special year in Analytic Number Theory. That has brought many number theorists to the institute already, so there will be a lot of people to talk to.

Last year I promised to hold a math party during the program. But I had to cancel it due to a scheduling conflict with George Hart's ZomeTool Workshop. I am planning a party this year. Either way, we'll have fun.
If you want to learn about the Langlands program, to spent time on the beautiful grounds of the Institute, to eat in one of the best cafeterias around, and to make new friends with other women interested in number theory, then please apply. The application deadline is February 20.
Suppose you want to increase your chances of winning the lottery jackpot by pooling money with a group of coworkers. There are several issues you should keep in mind.
When you pool the money and you hit the jackpot, the money has to be split. If you bought 10,000 tickets and the jackpot that you win is $100 million, then each ticket is entitled to a mere $10,000. Your chances of hitting the jackpot in the first place are 1 in 17,500 and you're not going to get rich off what you win.
Perhaps you'd be satisfied with a small profit. However, as I calculated in my previous piece on the subject, even if you include the jackpot in the calculation of the expected return, the Mega Millions game never had, and probably never will have a positive return.
Despite this fact, people continue to pool money in the hopes of winning big. However, there are more problems in doing this than just its non-profitability.
Consider a scenario. Your coworkers collected $1,000 to buy 1,000 lottery tickets. You give the money to Jerry who buys the tickets. Jerry can go to a store and buy 1,005 tickets. After the lottery he checks the tickets, takes the best five for himself and comes back to work with 1,000 disappointing tickets.
It is more likely that Jerry is cheating or that he will lose the tickets than it is that your group will win the jackpot. But there is a probabilistic way to check Jerry's integrity. According to the odds, every 40th ticket in Mega Millions wins something. Out of 1,000 tickets that Jerry bought, you should have about 25 that win something. If Jerry systematically brings back tickets that win less often than expected, you should replace Jerry with someone else.
There are methods to protect your group against cheating. For example, you can ask another person to join Jerry in purchasing the tickets, which they then seal in an envelope that they both sign.
Alternatively, you yourself could be the person responsible for buying 1,000 tickets. How would you protect yourself from suspicion of cheating? The same way as I mentioned above: bring along some witnesses and have everyone sign the sealed envelope.
The most reliable way to prevent Jerry from cheating is to have him write down all the ticket numbers and send this information to everyone before the drawing. This way he can't replace one ticket with another. But this is a lot of work for tickets that are usually worth less than the money you collected to buy them.
But there are other kinds of dangers if you use this supposedly reliable method. If you bought a lot of tickets the probability of winning a big payoff increases. Suppose Jerry publicly locks the envelope in a desk drawer in his office. If one ticket wins $10,000, and everyone knows all the ticket combinations, suddenly Jerry's desk drawer becomes a very unsafe place to keep the tickets.
Scams are not your only worry. You shouldn't buy the same combination twice — whether picking randomly or not. You really do not want to waste a ticket and end up sharing the jackpot with yourself.
You cannot change the odds of hitting the jackpot, but you can change the odds of sharing it with others. Indeed, there are people who do not buy random combinations, but rather pick their favorite numbers, like birthdays. You can reduce the probability of sharing the jackpot if you choose the combinations for your tickets wisely, by picking numbers that other people are unlikely to pick.
Still want to try the lottery? If you feel a need to throw your money away, instead of buying lottery tickets, feel free to donate to this blog.
In one of my previous pieces, I discussed returns on the Mega Millions lottery game, assuming that you buy a small number of tickets. In such a case winning the jackpot has zero probability. So I argued that if you want to estimate the profitability of the lottery as an investment, you have to remove the jackpot money from the calculation.
Today I will discuss what the formal expected return is. That is, I will include the jackpot money in the calculation. Since I argued against including the jackpot in my last article, you might wonder why I've then turned around to look into this.
I think this mathematical exercise will be fun. Besides, on a practical note, it is useful to know when the formal expected return is more than 100%, because then it might make sense to pool money with other people. Keep in mind though that if you want a chance to hit the jackpot, the total number of tickets you buy must be really big. For example, even if you manage to pool $10,000 for tickets, your probability of winning the jackpot in Mega Millions is only one in 17,500 — still minuscule.
If you buy only one ticket, you'll lose. If you manage to pool a lot of money and the probability of the jackpot becomes noticeable, that is, non-zero, could the jackpot be large enough that the lottery becomes a good investment?
For this calculation, I'm still assuming that you buy a relatively small number of tickets. If you buy millions of tickets the calculation is slightly different, and I will write about that later.
You might think that when the jackpot is bigger than the odds, it makes sense to play. I am discussing the Mega Millions game, where the odds of winning the jackpot are one in 175 million. So if the jackpot is more than $175 million, then it is profitable to play. Right?
Wrong. As I mentioned in my previous piece, after reducing for taxes, you get about 16% of your money back through smaller payouts. Hence, you need to recover the other 84% through the jackpot. So the jackpot should be more than 175*.84 = 147 million dollars. This sounds even better. Right?
Wrong. No one receives the jackpot. Winners can chose to immediately receive the lump sum, which equals the money lottery organizers have actually set aside for it. Alternatively, the lottery organizers can invest the lump sum and give winners a yearly distribution over many years, the total of which will equal the jackpot.
Suppose for simplicity the lump sum is half of the jackpot. That means we need the jackpot to be $294 million ($147 x 2). Right?
Oops. As usual, we forgot about taxes. To exacerbate your pain, I have to add that the winnings are taxable. Suppose you have to pay 30% from the jackpot. That means the jackpot needs to be $424 ($294/0.7) million in order to justify pooling money. OK?
We haven't seen jackpots that big yet. But neither have we finished the calculation. There is a probability that you might have to share the jackpot with other winners. To calculate this probability, we need to calculate the number of tickets sold. That means, your expected return depends not only on the size of the jackpot, but also on the number of these tickets.
But even if you know the number of tickets sold, we cannot calculate the expected returns precisely because people don't always buy tickets with random combinations, but often pick their own numbers.
When the jackpot is large people start buying tons of tickets, so we can expect that many of them buy quick-picks. Let us assume for now that the vast majority of people do not choose their own numbers, but buy tickets at random. Suppose 200 million tickets were sold. That is a very big number. Last time that many tickets were sold was when the jackpot was $390 million in March 2007. By the way, that was the largest jackpot ever.
In order to finish the calculation, we need to establish the probability of several winners, given that 200 million random tickets were sold:
| Number of winners | Probability |
|---|---|
| No winner | 0.3204 |
| One winner | 0.3647 |
| Two winners | 0.2075 |
| Three winners | 0.0787 |
| Four winners | 0.0224 |
| Five winners | 0.0051 |
| Six winners | 0.0010 |
From here we can calculate the adjustment coefficient, that is, the proportion of money you are expected to get from the jackpot given that there are 200 million players in the game. The coefficient is calculated from the table above as (0.3647 + 1/2*0.2075 + 1/3*0.0787 +1/4*0.0224 + 1/5*0.0051 + 1/6*0.0010)/(1 - 0.3204), and is equal to 0.7379. We need to divide our previous figure of $424 million by the adjustment coefficient. The result is $575 million.
Given that a $390 million jackpot attracted more than $200 million in tickets, we can expect that the $575 million jackpot will make people completely crazy and attract even more money. So I do not anticipate that the Mega Millions game will ever have a positive formal expected gain. My conclusion is that not only is there no financial sense in buying a single lottery ticket, but also none in pooling money.
Of course, you can buy tickets for non-financial reasons, like pumping up your adrenaline. In any case, I showed you the method to calculate your expected return, or, more appropriately, your expected loss.
Here is a fun math activity I use with my students, after I teach them to play the game of set. To other teachers — feel free to clone this idea.
First, I ask the students if they know what a magic square is. They usually do know that a magic square is a three-by-three square of distinct digits, so that every row, column and diagonal has the same sum. Then I ask them what a magic set square might be. Often they guess correctly that it is a three-by-three square made of set cards, so that every row, column and diagonal form a set. Once that's established, I have them build magic set squares.

While they're building them, I ask a lot of questions, from how many cards there should be in the deck to how many different sets there are.
Once the squares are built, I ask them what a magic set cube might be. Their next task is to use their magic set squares as the bottom layer in building magic set cubes. In order to see all the cards in the cube, I instruct them to arrange the layers (bottom, middle and top) side-by-side.

As they're working on their cubes, I continue quizzing them. How many main diagonals does a cube have? Once they confirm that the answer is four, I ask them to show me those diagonals in their magic set cubes and check that they are sets. I might also ask them how many different magic set squares should be inside a magic cube. This is a theoretical math question they need to answer before finding them in their own model. Next they need to identify the different sets that form lines inside their cubes.
At this point, some students guess my next request: to construct a magic set hypercube.

After students build their hypercubes, they never want to destroy them. They like comparing the different hypercubes and often take photos of them. If there's still time left, I can continue in several directions. For example, they can count the main diagonals of the hypercube and find them in their models. Alternatively, they can find a "no set" — the largest possible set of cards inside a magic set hypercube that doesn't contain a set.
Math is usually about thinking, but this is one activity the students can do with their hands. And that adds another layer of magic.
I promised to discuss how to improve the accuracy of your guessing at AMC 10/12, or other tests for that matter. There are two types of guessing. First, meta-guessing is when you do not look at the problem, but rather guess from just looking at the choices. Second, in the one I refer to as an educated-guess you do look at the problem. Instead of completely solving it, you try to deduce some information from the problem that will help you eliminate some of the choices. In this essay, I discuss both methods.
But first let me emphasize that solving problems is a more important skill than meta-guessing from a list of choices. Solving problems not only teaches you to think mathematically, but also increases your brain power. Spending time improving your meta-guessing skills can help you at multiple-choice tests and may give you insight into how test designers think, but this will not increase your math knowledge in the long run.
On the other hand, educated-guessing is a very useful skill to obtain. Not only can it improve your score during a test, the same methods can be applied to speed up the process of re-checking your answers before handing in the test. This skill will also come in handy when you start your research. Some problems in research are so difficult that even minor progress in estimating or describing your answer is beneficial.
Before discussing particular methods, let me remind you that AMC 10/12 is a multiple-choice competition with five choices for each question. The correct answer brings you 6 points. A wrong answer brings you 0 points, and not answering brings you 1.5 points. So if you randomly guess one of the five choices, your expected average score is 1.2 points, which is 0.3 less than your score for an unanswered question. Thus guessing is unprofitable on average.
However, if you can eliminate one choice, your expected average score becomes 1.5 points. In this case guessing doesn't bring you points on average, but it does create some randomness in your results. For strategic reasons, you might prefer guessing, as I discussed in my earlier piece.
If you can eliminate two wrong choices, then guessing becomes profitable. A random guess out of three possibilities brings you 2 points, a better result than 1.5 points for an unanswered question. Even more, if you can eliminate three choices, then guessing will increase your score by 3 points on average.
Now that we've covered the benefits of excluding choices before guessing, I would like to discuss how to exclude choices by just looking at them. Let us take one of the problems from the 2002 AMC10B. Here are the choices: (-2,1), (-1,2), (1,-2), (2,-1), (4,4). The pair (4,4) is a clear outlier. I suggest that an outlier can't be a correct choice. If (4,4) were the correct answer, then it would have been enough, instead of solving the problem, to use some intermediate arguments to choose it. For example, if you can argue that both numbers in the answer must be at least 2, or must be positive or be even, then you can get the correct answer without solving the problem. Any problem for which you can easily pick the correct answer without solving it is an unacceptably poor problem design. Thus, (4,4) can't be the correct answer, and should be eliminated during guessing.
Let us look at a 2002 AMC10A problem with the following choices: 4/9, 2/3, 5/6, 3/2, 9/4. Test designers want to create choices that are plausible. They try to anticipate possible mistakes. In this set of choices, we can deduce that one of the mistakes that they anticipate is that students will confuse a number with its inverse. In this case 5/6 can't be the correct answer. Otherwise, 6/5 would have been included as a choice. In another similar example from the 2000 AMC10 with choices -2, -1/2, 1/3, 1/2, 2, the designers probably hope that students will confuse numbers with their inverses and negations. Hence, we can exclude 1/3.
Sometimes the outlier might hint at the correct answer. Suppose you have the following list of choices: 2, 1/2π, π, 2π, 4π. The number 2 is an outlier here. Probably, the problem designers were contemplating that students might forget to multiply by π. In this case the likely correct answer would be 2π, because only from this answer can you get 2 by forgetting to multiply by π.
As an exercise, try to eliminate the wrong choices from the following set from a problem given at 2000 AMC10: 1/(2m+1), m, 1-m, 1/4m, 1/8m2.
AMC designers know all of these guessing tricks, so they attempt to confuse the competitors from time to time by going against common sense. For example, in a 2002 AMC10A problem the choices were: -5, -10/3, -7/3, 5/3, 5. I would argue that -7/3 is a clear outlier because all the others are divisible by 5. Furthermore, there is no point in including so many answers with 3 in the denominator unless there is a 3 in the denominator of the correct answer. So I would suggest that one of -10/3 and 5/3 must be the answer. My choice would be 5/3, as there is a choice of 5 which I would assume is there for students who forgot to divide by 3. As I said the designers are smart and the actual answer is -10/3. They would have tricked me on this problem.
One of the best ways to design a multiple choice question is to have an arithmetic progression as a list of choices. There is no good way to eliminate some choices from 112, 113, 114, 115, 116. Unfortunately for people who want to get an advantage by guessing, many of the problems at AMC have an arithmetic progression as their choices.
Now that we've seen the methods of meta-guessing, let's look at how to make an educated guess. Let us look at problem 1 in 2003 AMC10A.
What is the difference between the sum of the first 2003 even counting numbers and the sum of the first 2003 odd counting numbers?
Without calculations we know that the answer must be odd. Thus, we can immediately exclude three out of five choices from the given choices of 0, 1, 2, 2003, 4006. Parity consideration is a powerful tool in eliminating wrong answers. Almost always you can decide the parity of the answer much faster than you can calculate the answer. Similar to using parity, you can use divisibility by other numbers to have a fast elimination. Here is a problem from 2000 AMC10:
Mrs. Walter gave an exam in a mathematics class of five students. She entered the scores in random order into a spreadsheet, which recalculated the class average after each score was entered. Mrs. Walter noticed that after each score was entered, the average was always an integer. The scores (listed in ascending order) were 71, 76, 80, 82, and 91. What was the last score Mrs. Walter entered?
The first four numbers entered must be divisible by 4. The total of the given numbers is divisible by 4. Hence, the last number must also be divisible by 4. This reasoning eliminates three out of five choices.
Another powerful method is a rough estimate. Let us look at the next problem in 2003 AMC10A.
Members of the Rockham Soccer League buy socks and T-shirts. Socks cost $4 per pair and each T-shirt costs $5 more than a pair of socks. Each member needs one pair of socks and a shirt for home games and another pair of socks and a shirt for away games. If the total cost is $2366, how many members are in the League?
If we notice that the cost per person is more than $25, we can conclude that there are less than a hundred members in the League. Given the choices of 77, 91, 143, 182, and 286, we immediately can eliminate three of them.
Another method is to use any partial knowledge that you may have. Consider this problem from 2003 AMC10A:
Pat is to select six cookies from a tray containing only chocolate chip, oatmeal, and peanut butter cookies. There are at least six of each of these three kinds of cookies on the tray. How many different assortments of six cookies can be selected?
You might remember that there is a formula for this. Even if you do not remember the exact formula, you might still have a vague memory that the answer must be a binomial coefficient that somehow uses the number of cookies and the number of flavors. Looking at the choices — 22, 25, 27, 28, 29 — you can see that the only choice that appears in the first 10 rows of the Pascal's triangle is 28. So you should go with 28.
It is easy to talk about easy problems; let us see what we can do about difficult ones. Consider the last problem on 2003 AMC10A:
Let n be a 5-digit number, and let q and r be the quotient and the remainder, respectively, when n is divided by 100. For how many values of n is q+r divisible by 11?
The choices are 8180, 8181, 8182, 9000, 9090. They can be naturally split into two groups: three choices below 9000 and the rest. By my rules of removing outliers the group of numbers below 9000 seems the more promising group. But I would like to discuss how to approximate the answer. There is no reason to believe that there is much correlation between remainders by 100 and divisibility by 11. There is a total of 90,000 5-digit numbers; among those numbers, approximately 90,000/11 = 8182 is divisible by 11, so we should go with the group of answers close to 8182.
Another way of thinking about this problem is the following. There are 900 different quotients by 100 to which we add numbers between 0 and 99. Thus for every quotient our sums are a set of 100 consecutive numbers. Out of 100 consecutive numbers usually 9, and rarely 10, are divisible by 11. Hence, the answer has to be less than 9000.
Sometimes methods you use for guessing can bring you the answer. Here is a problem from 2001 AMC12:
What is the product of all odd positive integers less than 10000? (A) 10000!/5000!2, (B) 10000!/25000, (C) 9999!/25000, (D) 10000!/(250005000!), (E) 5000!/25000.
For a rough estimate, I would take a prime number and see in what power it belongs to the answer. It's simplest to consider a prime number p that is slightly below 5000. Then p should appear as a factor in the product of all odd positive integers below 10000 exactly once. Now let us look at the choices. Number p appears in 5000! once and in 10000! twice (as p and 2p). Hence, it appears in (A) zero times, and twice each in (B) and (C). We also can rule out (E) as the product of odd numbers below 10000 must be divisible by primes between 5000 and 10000, but 5000! doesn't contain such primes. Thus the answer must be (D).
The method I just described won't produce the formula. But the ideas in this method allow you to eliminate all the choices except the right one. Moreover, this method provides you with a sanity check after you derive the formula. It also helps to build your mathematical intuition.
I hope that you will find my essays about AMC useful. And good luck on February 9!
I teach students to solve math problems by appreciating the big picture, or by noticing the problem's inner symmetries, or through a deep understanding of the problem. In the long run, one thing leads to another: such training structures their minds so that they are better at understanding mathematics and, as a consequence, they perform well at math competitions.
That is why, when AMC is still far away, I do not give my students a lot of AMC problems; rather, I pick problems that contain useful ideas. When I do give AMC problems, I remove the multiple choices, so they understand the problems completely, instead of looking for shortcuts. For example, this problem from AHSME 1999 is a useful problem with or without choices.
What is the largest number of acute angles that a hexagon can have?
As AMC approaches, we start discussing how to solve problems given multiple choices. Training students for AMC is noticeably different from teaching mathematics. For example, some problems are very specific to AMC. They might not even exist without choices. Consider this problem from the 2001 AMC12:
A polynomial of degree four with leading coefficient 1 and integer coefficients has two zeros, both of which are integers. Which of the following can also be a zero of the polynomial?
Here we really need the choices in order to pick one complex number, such that its real part is an integer or a half integer and, in addition, the product of the number with its conjugate produces an integer.
Sometimes the choices distract from solving the problem. For example, in the following problem from the 2005 AMC12, having choices might tempt students to try to eliminate them one by one:
The sum of four two-digit numbers is 221. None of the eight digits is 0 and no two of them are same. Which of the following is not included among the eight digits?
Without the choices, students might start considering divisibility by 9 right away.
On some occasions, the choices given for the problems at AMC make the problem more interesting. Here is an example from the 2000 AMC10:
Two different prime numbers between 4 and 18 are chosen. When their sum is subtracted from their product, which of the following numbers could be obtained?
The choices are 21, 60, 119, 180 and 231. We can immediately see that the answer must be odd. Because the span of the three remaining choices is so wide, we suspect that we can eliminate the smallest and the largest. Trying for 5 and 7 — the two smallest primes in the range — we can eliminate 21. Similarly, checking the two largest primes in the range, we can eliminate 231. This leaves us with the answer: 119. If the choices were different, we might have lost the interplay between the solution and the list of choices. Then, solving the problem would have been slower and more boring. There are ten pairs of prime numbers to check. And we would need on average to check five of them until we stumbled on the correct choice.
In other cases having multiple choices makes the problem more boring and less educational. Here is another problem from the same competition.
Two non-zero real numbers, a and b, satisfy ab = a – b. Find a possible value of a/b + b/a – ab.
Solving this problem without choices can teach students some clever tricks that people use when playing with expressions. Indeed, when we collect a/b + b/a into one fraction (a2 + b2)/ab, we might remember that a2 + b2 is very close to (a – b)2, and see from here that a/b + b/a – 2 is (a – b)2/ab, which, given the initial condition, equals ab. Thus, we can get the answer: 2.
On the other hand, if you look at the multiple choices first: -2, -1/2, 1/3, 1/2, 2, you might correctly assume that the answer is a number. Thus, the fastest way to solve it is to find an example. If a = 1, then b must be 1/2, and the answer must be 2. This solution doesn't teach us anything new or interesting.
My next example from the 2002 AMC10 is similar to the previous one. The difference is that the solution with multiple choices is even more boring, while the solution without these choices is more interesting and beautiful.
Let a, b, and c be real numbers such that a – 7b + 8c = 4 and 8a + 4b – c = 7. Then a2 – b2 + c2 is: 0, 1, 4, 7, or 8.
Given the choices, we see that the answer is a number. Hence we need to find any solution for the system or equations: a – 7b + 8c = 4 and 8a + 4b – c = 7. For example, if we let c = 0, we have two linear equations and two variables a and b that can be solved by a straightforward computation. Then we plug the solution into a2 – b2 + c2.
Without knowing that the result is a number, we need to look at the symmetries of our two initial equations. We might discover a new rule:
If we have two expressions ax + by and bx – ay, where a and b are switched between variables and there is a change in sign, it is a good idea to square each of them and sum them up, because the result is very simple: (a2 + b2)(x2 + y2).
Hence, in our initial problem we need to move the term with b in our two linear equations to the right; then square them and sum up the results. This way we may get a very simple expression. And indeed, this trick leads to a solution and this solution provides insight into working with algebraic expressions.
This is the perfect problem to linger over, assuming you're not in the middle of a timed competition. It might make you wonder for which parameters this problem works. You might discover a new theorem that allows you to create a very similar problem from any number that can be represented as a sum of two non-trivial squares in two different ways.
To prepare my students for AMC I need to teach them tricks that are not useful at USAMO, or in mathematics in general for that matter. Many tricks distract from new ideas or from understanding the problem. All they give us is speed.
This bothers me, but to pacify myself, I keep in mind that most of my students will not become mathematicians and it might be useful in their lives to be able to make split-second decisions among a small number of choices.
However, it seems like Americans have the opposite problem: we make quick decisions without thinking. I'm concerned that training for multiple choice tests and AMC competitions aggravates this problem.
What object is missing?
Should you try to guess an answer to a multiple-choice problem during a test? How many problems should you try to guess? I will talk about the art of boosting your guessing accuracy in a later essay. Now I would like to discuss whether it makes sense to pick a random answer for a problem at AMC 10.
Let me remind you that each of the 25 problems on the AMC 10 test provides five choices. A correct answer brings you 6 points, a wrong answer 0 points and not answering at all gives you 1.5 points. So guessing makes the expected average per problem to be 1.2 points. That is, on average you lose 0.3 points when guessing. However, if you are lucky, guessing will gain you 4.5 points per problem, and if you are unlucky, it will lose you 1.5 points per problem.
So we see that on average guessing is unprofitable. But there are situations in which you have nothing to lose if you get a smaller score and a lot to gain if you get a better score. Usually the goal of a competitor at AMC 10 is to get to AIME. For that to happen, you need to get 120 points or be in the highest one percentile of all competitors. This rule complicates my calculations. So I decided to simplify it and say that your goal is to get 120 points and then see what mathematical results I can get out of that simplification.
First, suppose you are so accurate that you never make mistakes. If you have solved 20 problems, then your score without guessing is 127.5. If you start guessing and guess wrongly for all of the last five questions, you still have your desired 120 points. In this instance it doesn't matter whether you guess or not.
Suppose on the other hand that you are still accurate, but less powerful. You have only solved 15 problems, so your score without guessing is 105. Now you must be strategic. Your only chance to get to your goal of 120 points is to guess. Suppose you randomly guess the answers for the 10 problems you didn't solve. To make it to 120, you need to guess correctly at least five out of the ten remaining problems. The probability of doing so is 3%. Here is a table of your probability of making 120 points if you solve correctly n problems and guess the other problems.
| n | Probability |
|---|---|
| 20 | 1.0 |
| 19 | 0.74 |
| 18 | 0.42 |
| 17 | 0.20 |
| 16 | 0.09 |
| 15 | 0.03 |
| 14 | 0.01 |
| 13 | 0.004 |
| 12 | 0.001 |
We can see that if you solved a small number of problems, then the probability of getting 120 points is minuscule; but as the number of problems you solved increases, so does the probability of getting 120 points by guessing.
The interesting part is that if you have solved 19 problems, you are guaranteed to get to AIME without guessing. On the other hand, if you start guessing and all your guesses are wrong, you will not pass the 120 mark. The probability of having all six problems wrong is a not insignificant 26%. In conclusion, if you are an accurate solver and want to have 120 points, it is beneficial to guess the remaining problems if you solved fewer than 19 problems. It doesn't matter much if you solved fewer than 10 problems or more than 19. But you shouldn't guess if you solved exactly 19.
If you are not 100% accurate things get more complicated and more interesting. To decide about guessing, it is crucial to have a good estimate of how many mistakes you usually make. Let's say that you usually have two problems wrong per AMC test. Suppose you gave answers to 20 problems at AMC. What's next? Let us estimate your score. Out of your 20 answers you are expected to get 18*6 points for them plus 5*1.5 points for the problems you didn't answer. Your expected score is 115.5. You are almost there. You definitely should guess. But does it matter how many questions you are trying to guess?
The correct answer to one question increases your score by 4.5 with probability 0.2, and the wrong answer decreases your score by 1.5 with probability 0.8. One increase by 4.5 is enough for you goal of 120 points. So if you guess one question, with probability 0.2, you get 120 points. If you guess two questions, then your outcome is as follows: you increase your score by 9 points with probability 0.04; you increase your score by 3 points with probability 0.32; and you decrease your score by 3 points with probability 0.64. As you need at least a 4.5 increase in points, it is not enough to guess one question out of two. You actually need to guess correctly on both of them. The probability of this happening is 0.04. It is interesting, but you have a much greater chance to get to your goal if you guess just one question than if you guess two. Overall, here is the table of probabilities to get to 120 points where m is the number of questions you are guessing.
| m | Probability |
|---|---|
| 0 | 0 |
| 1 | 0.20 |
| 2 | 0.04 |
| 3 | 0.10 |
| 4 | 0.18 |
| 5 | 0.26 |
Your best chances are to guess all the remaining questions.
By the end of the test you know how many questions you answered, but you don't know how many errors you made. The table below tells you what you need in order to get 120 points. Here is how you read the table: The number of problems you solved is in the first column. If you are sure that the number of mistakes is not more than the number in the second column, you can relax as you made at least 120 points. The last column gives the score.
| Answered problems | Mistakes you can afford | Score |
|---|---|---|
| 19 | 0 | 123.0 |
| 20 | 1 | 121.5 |
| 21 | 2 | 120.0 |
| 22 | 2 | 124.5 |
| 23 | 3 | 123.0 |
| 24 | 4 | 121.5 |
| 25 | 5 | 120.0 |
If the number of mistakes you made is one more than in the corresponding row of the table, you should start guessing in order to try to get 120 points. Keep in mind that there is a risk: if you are not sure how many problems you solved already and start guessing, you might ruin your achievement of 120 points.
In the next table I show how many questions you can guess without the risk of going below 120 points. The word "all" means that it is safe to guess all the remaining questions.
| Answered problems | Mistakes you can afford | Score | Non-risky guesses |
|---|---|---|---|
| 19 | 0 | 123.0 | 2 |
| 20 | 1 | 121.5 | 1 |
| 21 | 2 | 120.0 | 0 |
| 22 | 2 | 124.5 | all |
| 23 | 3 | 123.0 | all |
| 24 | 4 | 121.5 | all |
You can see that if your goal is to get 120 points, your dividing line is answering 22 questions. If you solved 22 questions or more, there is no risk in guessing. Namely, if you have already achieved more than 120 points, guessing will not take you below that. But if you made more errors than are in the table, then guessing might be beneficial. Hence, you should always guess in this case — you have nothing to lose.
Now I would like to show you my calculations for a situation in which you are close to 120 points and need to determine the optimum number of questions to guess. The first column is the number of answered questions. The second column is the number of mistakes. The third column is your expected score without guessing. The fourth column is the optimum number of questions you should guess. And the last column lists your chances to get 120 points if you guess the number of questions in the fourth column.
| Answered problems | Mistakes | Score | Questions to guess | Probability of success |
|---|---|---|---|---|
| 17 | 0 | 114.0 | 8 | 0.20 |
| 18 | 0 | 118.5 | 7 | 0.42 |
| 18 | 1 | 112.5 | 7 | 0.15 |
| 19 | 1 | 117.0 | 2 | 0.36 |
| 19 | 2 | 111.0 | 6 | 0.10 |
| 20 | 2 | 115.5 | 5 | 0.26 |
| 21 | 3 | 114.0 | 4 | 0.18 |
| 22 | 3 | 118.5 | 3 | 0.49 |
| 22 | 4 | 112.5 | 3 | 0.10 |
| 23 | 4 | 117.0 | 2 | 0.36 |
| 23 | 5 | 111.0 | 2 | 0.04 |
| 24 | 5 | 115.5 | 1 | 0.20 |
You can see that almost always if you are behind your goal, you should try to guess all of the remaining questions, with one exception: if you answered 19 questions and one of them is wrong. In this case you should guess exactly two questions — not all that remain.
Keep in mind that all these calculations are very interesting, but don't necessarily apply directly to AMC 10, because I simplified assumptions about your goals. It may not be directly applicable, but I hope I have expanded your perspective about how you can use math to help you understand how better to succeed at math tests and how to design your strategy.
I plan to teach you how to guess more profitably, and this skill will also advance your perspective.
Last revised October 2013