This blog has a modern version at http://blog.tanyakhovanova.com/, where you can leave comments. This page contains the copies of 134 blog entries for 2011 and 2012. The latest essays are at http://www.tanyakhovanova.com/MathBlog.html
One of the 2012 PRIMES projects, suggested by Professor Jacob Fox, was about bounds on the number of halving lines. I worked on this project with Dai Yang.
Suppose there are n points in a general position on a plane, where n is an even number. A line through two given points is called a halving line if it divides the rest of n−2 points in half. The big question is to estimate the maximum number of halving lines.
Let us first resolve the small question: estimating the minimum number of halving lines. Let's take one point from the set and start rotating a line through it. By a continuity argument you can immediately see that there should be a halving line through any point. Hence, the number of halving lines is at least n/2. If the point is on the convex hull of the set of points, then it is easy to see that it has exactly one halving line through it. Consequently, if the points are the vertices of a convex n-gon, then there are exactly n/2 halving lines. Thus, the minimum number of halving lines is n/2.
Finding the maximum number of halving lines is much more difficult. Previous works estimated the upper bound by O(n4/3) and the lower bound by O(ne√log n). I think that Professor Fox was attracted to this project because the bounds are very far from each other, and some recent progress was made by elementary methods.
Improving a long-standing bound is not a good starting point for a high school project. So after looking at the project we decided to change it in order to produce a simpler task. We decided to study the underlying graph of the configuration of points.
Suppose there is a configuration of n points on a plane, and we are interested in its halving lines. We associate a graph to this set of points. A vertex in the configuration corresponds to a vertex in the graph. The graph vertices are connected, if the corresponding vertices in the set have a halving line passing through them. So we decided to answer as many questions about the underlying graph as possible.
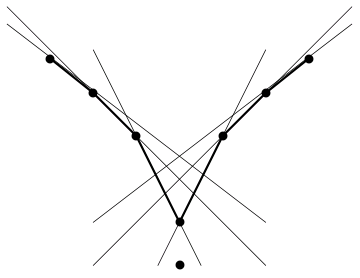
For example, how long can the longest path in the underlying graph be? As I mentioned, the points on the convex hull have exactly one halving line through them. Hence, we have at least three points of degree 1, making it impossible for a path to have length n. The picture below shows a configuration of eight points with a path of length seven. We generalized this construction to prove that there exists a configuration with a path of length n−1 for any n.

We also proved that:
After we proved all these theorems, we came back to the upper bound and improved it by a constant factor. Our paper is available at arXiv:1210.4959.
Samuel Hansen has an unusual profession: he is a mathematics podcaster. He interviewed me for his Relatively Prime podcast titled 0,1,2,3,…, where we discussed my Number Gossip project. The podcast also includes interviews with Neil Sloane, Michael Shamos, and Alex Bellos.
My previous interview with Samuel is at acmescience.com. There I discuss both math education and gender in math issues.
When I listened to myself, I found it strange that I seemed to have a British accent on top of my Russian accent. Did you notice that too?
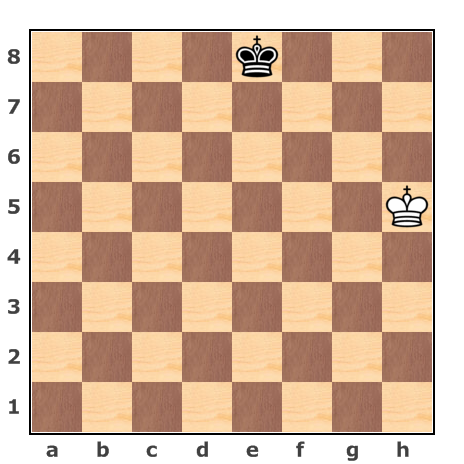
I discovered the following chess puzzle on a Russian blog for puzzle lovers. It is a helpmate-type puzzle. Black cooperates with White in checkmating himself. In this particular puzzle Black starts and helps White to win in one move.
Oops. Something is not quite right. There are not enough pieces on the board. To recover the missing pieces in order to solve the puzzle, you need to retrace your steps. If Black and White go back one move each, they will be able to cooperatively checkmate Black in one move. Find the position one move back and the cooperative checkmate.
I am Russian; I know how to play chess. My father taught me when I was three or four. We played a lot and he would always win. I got frustrated with that and one day, when I was five, I didn't announce my check. On the next move, I grabbed his king and claimed my victory.
He was so angry that he turned red and almost hit me. This frightened me so much that I lost my drive for chess that very moment.
I still understand its beauty and solve a chess problem about once a decade. Look for a cute chess puzzle in my next post.
For my every class I try to prepare a challenge problem to stretch the minds of my students. Here is a problem I took from Adam A. Castello's website:
There is a ceiling a hundred feet above you that extends for- ever, and hanging from it side-by-side are two golden ropes, each a hundred feet long. You have a knife, and would like to steal as much of the golden ropes as you can. You are able to climb ropes, but not survive falls. How much golden rope can you get away with, and how? Assume you have as many hands as you like.
The next problem I heard from my son Sergei:
You are sitting at the equator and you have three planes. You would like to fly around the equator. Each plane is full of gas and each has enough gas to take you half way around. Planes can transfer gas between themselves mid-air. You have friends, so that you can fly more than one plane at once. How do you fly around the equator?
* * *
Right clicking a file with a mouse will allow you to change it, check it for viruses, or revert to the previous version. I wonder where I can buy a mouse that can do the same thing with my husband.
* * *
— Let's have sex.
— Sure, but today I want to be the numerator.
* * *
Attention! We want to check that you are not a robot. Please, undress and turn on a web-camera.
* * *
In a drug store:
— I would like input and output cleaners.
— ???
— Toothpaste and toilet paper.
* * *
I used to recount the multiplication tables to delay my ejaculation. Now, each time I see the multiplication tables I get a hard on.
* * *
— Tonight my parents are away. Let's finally try a forbidden thing.
— Dividing by zero?
* * *
My friend put his mistress in his phone's contact list as 'low battery'.
In what base does 2012! have more trailing zeros: base 15 or 16?
Explain why the result shouldn't be too surprising.
I would like to report on my weight loss progress. Last time I added two new habits, walking my toy dog every day, and drinking more water from the enticing cute bottles I bought.
I named my stuffed dog Liza and I walk with her every day. I didn't expect immediate weight loss due to this new regime, because my first goal was to get out of the house every day, even if only for two seconds. The next step will be to increase walking time to ten minutes.
Drinking a lot of water doesn't work well. I spend too much time looking for bathrooms and panicking that I will not make it. I like the idea of drinking a lot of water, but I am not sure I can hold to it, if you understand what I mean.
Since taking on this challenge, I've gained two habits, but I haven't lost a pound.
Now I'm upping my game. Below is my analysis of why I eat. When I eat, I believe that I am hungry. But looking at this more objectively I think this is not always the case: sometimes there are other reasons. I am listing these other reasons so I can fight them face-to-face. Here we go:
Hmm. That was painful to write. My psychoanalyst taught me that pain means I am on the right track.
Davidson Institute for Talent Development announced their 2012 Winners. Out of 22 students, three were recognized for their math research. All three of them are ours: that is, they participated in our PRIMES and RSI programs:
I already wrote about Xiaoyu's project. Today I want to write about Sitan's project and what I do as the math coordinator for RSI.
RSI students meet with their mentors every day and I meet with students once a week. On the surface I just listen as they describe their projects. In reality, I do many different things. I cheer the students up when they are overwhelmed by the difficulty of their projects. I help them decide whether they need to switch projects. I correct their mistakes. Most projects involve computer help, so I teach them Mathematica. I teach them the intricacies of Latex and Beamer. I explain general mathematical ideas and how their projects are connected to other fields of mathematics. I never do their calculations for them, but sometimes I suggest general ideas. In short, I do whatever needs to be done to help them.
I had a lot of fun working with Sitan. His project was about the rank number of grid graphs. A vertex k-ranking is a labeling of the vertices of a graph with integers from 1 to k so that any path connecting two vertices with the same label passes through a vertex with a greater label. The rank number of a graph is the minimum possible k for which a k-ranking exists for that graph. When Sitan got the project, the ranking numbers were known for grid graphs of sizes 1 by n, 2 by n, and 3 by n. So Sitan started working on the ranking number of the 4 by n graph.
His project was moving unusually fast and my job was to push him to see the big picture. I taught him that the next step, once he finishes 4 by n graphs is not to do 5 by n graphs, as one might think. After the first step, the second step should be bigger. He should use his insight and understanding of 4 by n graphs to try to see what he can do for any grid graphs.
This is exactly what he did. After he finished the calculation of the rank number of the 4 by n graphs, he found a way to improve the known bounds for the ranking number of any grid graph. His paper is available at the arXiv.
I just looked at my notes for my work with Sitan. The last sentence: "Publishable results, a potential winner."
PRIMES-USA: A new MIT program for talented math students from across the country.
I've been working as a math coordinator for RSI, the most competitive summer program for high school juniors. RSI arranges for these select students to do scientific research. I only work with kids who do math, and usually we have a dozen of them. Every student has an individual mentor, usually a graduate student, with whom they meet daily. I supervise all the projects and meet with each high school student about once a week. My job was described as "going for the biggest impact": when the project is in trouble, I jump in to sort it out; when the project is doing well, I push it to further limits.
RSI is a great program: kids enjoy it and we produce interesting research. My biggest concern is that the program is too short. The kids do math for five weeks and they usually approach a good result, but at the end of RSI we generally see just a hint of what they could truly achieve. Kids who continue to work on their own after the program ends are more successful. Unfortunately most of the students stop working at the end of the program just as they are approaching a big theorem.
I discussed this dissatisfying trend with Pavel Etingof and Slava Gerovitch and we decided to do something about it. Pavel and Slava conceived and found funding for a new program called PRIMES that is similar to RSI, but runs for a year. From February through May, PRIMES students meet with their mentors weekly. In fact, we require on the application that the students commit to coming to MIT once a week, thereby limiting us to local students. Theoretically, someone from Detroit with a private jet who can fly to MIT weekly would be welcomed.
Before the first year, we wondered whether the smaller pool of local students would be weaker than national and international RSI students. To our delight, that wasn't the case. In the first year we got fantastic students. One explanation is that PRIMES is much more flexible. We do not mind when our students go to IMO in the summer or to math camps or when they go away on vacation with their parents. As a result, we get students who would never apply to RSI because of their summer schedules. Our PRIMES students have won so many prizes that I do not remember them all. We post our successes on the website.
Our success in PRIMES suggests that there are likely many talented kids in other states who never even apply to RSI because of a scheduling conflict. This led us to try to adapt PRIMES to national needs. So we created a new program called PRIMES-USA that will accept students from across the country. We will work with them through Skype. These students must commit to travel to MIT for a PRIMES conference in May. Because this is our pilot program, we will only accept five students.
Thank you to everyone who helped me to find a host for my Number Gossip website. Some readers and friends even offered me free hosting on their servers. I decided to pay for hosting because I have many specific requirements and that might be a burden on my friends.
On the basis of my readers' recommendations, I chose Dreamhost as my new webhosting provider. I apologize for the interruption in the flow of the gossip. I know that many people use Number Gossip for birthday gift ideas. I can tell you that on my previous birthday, you could have congratulated me on becoming prime and evil.
I visited Raymond Smullyan on my way home from Penn State. We went for lunch at Selena's Diner. What do two mathematicians do during lunch? Exchange magic tricks and jokes, of course. Here is a story Raymond told me:
Raymond: What is the date?
Stranger: I do not know.
Raymond: But you have a newspaper in your pocket!
Stranger: It's no use. It's yesterday's.
Consider central symmetry: squares and circles are centrally symmetric, while trapezoids and triangles are not. But if you have two trapezoids, which of them is more centrally symmetric? Can we assign a number to describe how symmetric a shape is?
Here is what I suggest. Given a shape A, find a centrally symmetric shape B of the largest area that fits inside. Then the measure of central symmetry is the ratio of volumes: B/A. For centrally symmetric figures the ratio is 1, and otherwise it is a positive number less than 1.

The measure of symmetry is positive. But how close to 0 can it be? The picture on the left is a shape that consists of five small disks located at the vertices of a regular pentagon. If the disks are small enough than the largest symmetric subshape consists of two disks. Thus the measure of symmetry for this shape is 2/5. If we replace a pentagon with a regular polygon with a large odd number of sides, we can get very close to 0.
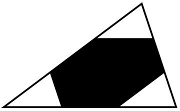
What about convex figures? Kovner's theorem states that every convex shape of area 1 contains a centrally symmetric shape of area at least 2/3. It is equal to 2/3 only if the original shape is a triangle. That means every convex shape is at least 2/3 centrally symmetric. It also means that the triangle is the least centrally symmetric convex figure. By the way, a convex shape can have only one center of symmetry.
After I started writing this I discovered that there are many ways in which people define measures of symmetry. The one I have defined here is called Kovner-Besicovitch measure. The good news is that the triangle is the least symmetric planar convex shape with respect to all of these different measures.
I'm trying to lose weight. Many books explain that dieting doesn't work, that people need to make permanent changes in their lives. This is what I have been doing for several years: changing my habits towards a healthier lifestyle.
This isn't easy. I am a bad cook; I hate shopping; and I never have time. Those are strong limitations on developing new habits. But I've been a good girl and have made some real changes. Unfortunately, my aging metabolism is changing faster than I can adopt new habits. Despite my new and improved lifestyle, I am still gaining weight.
But I believe in my system. I believe that one day I will be over the tipping point and will start losing weight, and it will be permanent. Meanwhile I would like to share with you the great ideas that will work someday.

I have many other ideas that for different reasons haven't yet become habits. So I am thinking about tricks to turn them into habits.
I have many more ideas, but I gotta run now. I need to walk my dog.

I received the book Taking Sudoku Seriously by by Jason Rosenhouse and Laura Taalman for review and put it aside to collect some dust. You see, I have solved too many Sudokus in my life. The idea of solving another one made me barf. Besides, I thought I knew all there is to know about the mathematics of Sudoku.
One day out of politeness or guilt I opened the book — and couldn't stop reading.
The book is written for people who like Sudoku, but hate math. This is so strange. Sudoku is math. People who are good at Sudoku are good at math, or at least they are supposed to be. It seems that math education in the United States is so bad that people who were born to be good at math and to like math, hate it instead. So the goal of the book is to establish a bridge from Sudoku to math. And the book does a superb job of it.
This well-written book moves from puzzles to discussions in such a natural way that math becomes a continuation of puzzles.
Taking Sudoku Seriously covers a lot of fun material: methods to solve Sudoku, how to count the number of different Sudoku puzzles, and how to find the smallest number of clues that are needed for a unique puzzle. The book travels into the neighboring area of Latin and Greco-Latin squares. While discussing all those fun things it covers groups, symmetries, number theory, graph theory (including book thickness) and more.
I am not the target audience for this book, because I do not need convincing that math is fun. The best part for me was the hundred puzzles. Only a portion of them were standard Sudoku puzzles — and I skipped those. The others were either Sudoku with a twist or plain math puzzles.
The puzzles are all very different and I was so excited by them, that I went ahead and solved them, and caught up with reading the text later. And I enjoyed both: reading and solving.
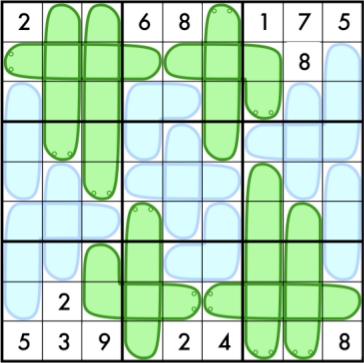
Here is puzzle 91 from the book. Fill in the grid so that every row, column, and block contains 1-9 exactly once. In addition, each worm must contain entries that increase from tail to head. For blue worms you must figure out yourself which end is the head.
It's easy to judge who is the fastest runner or swimmer. Judges do not need to be runners and swimmers themselves. They simply need a stopwatch and a camera.
Other competitions are more difficult to judge. Take for example the Fields medal. The judges need to be mathematicians. Since they can't be experts in all the different areas of mathematics, they have to rely on recommendation letters. The mathematicians who write recommendation letters are biased, because they are interested in promoting their own field. The committee's job is not simple, not the least because it involves a lot of politics. It is easy to award the medal to Grigory Perelman. He solved a high-profile long-standing conjecture. But other cases are not that straightforward.
Imagine a genius mathematician with a new vision. He or she might be so far ahead of everyone else, that the Fields committee would fail to appreciate the new concept. I wish the math community would create a list of mathematicians who deserved the Fields medal, but were passed over. As time goes by, perhaps a new Einstein will emerge on this list.
The reason the Fields committee more or less works is that the judges do not need to be as talented mathematicians as the awardees. They do not need to create mathematics, they need to understand it. And the latter is easier than the former.
A completely different story happens with IQ tests. Someone has to write those tests. There is no reason to think that writers of the IQ tests are anywhere close to the end tail of the IQ distribution. Hence, the IQ tests are not qualified to find the IQ geniuses.
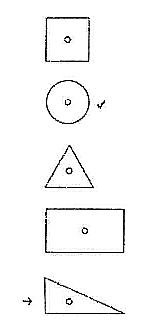
Now might be a good time to complain about the IQ test I took myself. Many years ago I tried an IQ test online through tickle.com. I was so disappointed with my non-perfect score that I never looked at my answers. Recently, while cleaning my apartment, I discovered the printout of the test. I made one mistake in the following question.
Which one of the designs is least like the other four?
The checkmark is the expected answer. They think that the circle is the odd one out because all the other shapes are polygons. The arrow points to my answer. I chose the right triangle because it is the only shape without symmetries. Who says that polygonality is more important than symmetry?
I recently received an invoice from Jumpline, Inc. requesting a payment for hosting www.tanya-khovanova-temp.com. I had never heard of Jumpline before and I didn't have a webpage with that address. So I thought that it was spam.
Because the invoice had my name and address, I decided to call them and check what was going on. It appeared that Jumpline had swallowed Hosting Rails, the company that was hosting my Number Gossip page. Still, I didn't have a clue what the invoice was about.
I asked the representative whether the web address was related to Number Gossip, and he said no. So I canceled the hosting. My work schedule is the busiest in July, so I forgot about the invoice and didn't check my website.
Then I received a letter from Christian, a Number Gossip fan, who told me that the website was down. I called Jumpline again.
It appears that the representative didn't know what he was doing and misled me. The web address www.tanya-khovanova-temp.com was an internal name for my Number Gossip site. They had deleted all the files and were unable to restore my website.
Now I have to decide what to do. I do not want to go back to Jumpline as they are very unprofessional in these ways:
Can anyone suggest a company that can host a website that is written in Ruby on Rails?
The Fibonacci sequence is all about addition, right? Indeed, every element Fn of the Fibonacci sequence is the sum of the two previous elements: Fn = Fn-1 + Fn-2. Looking closer we see that the Fibonacci sequence grows like a geometric progression φn, where φ is the golden ratio. In addition, the Fibonacci sequence is a divisibility sequence. Namely, if m divides n, then Fm divides Fn.
My point: we define the sequence through addition, and then multiplication magically appears by itself. What would happen if we tweak the rule and combine addition and multiplication there?
John Conway did just that: namely, he invented a new sequence, or more precisely a series of sequences depending on the pair of the starting numbers. The sequences are called Conway's subprime Fibonacci sequences. The rule is: the next term is the sum of the two previous terms, and, if the sum is composite, it is divided by its least prime factor.
Let me illustrate what is going on. First we start with two integers. Let's take 1 and 1 as in the Fibonacci sequence. Then the next term is 2, and because it is prime and we do not divide by anything. The next two terms are 3 and 5. After that the sum of two terms is 8, which is now composite and it is divided by 2. So the sequence goes: 1, 1, 2, 3, 5, 4, 3, 7, 5, 6, 11 and so on.
The subprime Fibonacci sequences excite me very much. Not only does adding some multiplication to the rule make sense to me, but also, the sequences are fun to play with. I got so excited that I even coauthored a paper about these sequences titled, not surprisingly, Conway's Subprime Fibonacci Sequences. The paper is written jointly with Richard K. Guy and Julian Salazar, and is available at the arXiv:1207.5099.
We can start a subprime Fibonacci sequence with any two positive numbers. You can see that such a sequence doesn't grow fast, because we divide the terms too often. We present a heuristic argument in the paper that allows us to conjecture that no subprime Fibonacci sequence grows indefinitely, but they all start cycling. The conjecture is not proven and I dare you to try.
Meanwhile, the sequences are a lot of fun and I suggest a couple of exercises for you:
By the way, a trivial cycle is the boring thing that happens if we start a sequence with two identical numbers n bigger than one: n, n, n, n, ….
Have fun.
Kvant is a very popular Russian math and physics journal for high school-children. My favorite page is the one with puzzles directed to younger readers. Here are two puzzles from the latest online issue: 2012 number 3.
The first one, by N. Netrusova, is optimistic about the next year.
An astrologist believes that a year is happy if its digit representation contains four consecutive digits. For example, the next year, 2013, will be happy. When was the previous happy year?
The second problem is by L. Mednikov and A. Shapovalov. It confused me at first. For a moment I thought that the best answer is 241 rubles:
A big candle lasts one hour and costs 60 rubles. A small candle lasts 11 minutes and costs 11 rubles. Can you measure a minute by spending not more than a) 200 rubles, b) 150 rubles?
My American friends often ask me for insights into why Grigory Perelman refused the one million dollar Clay prize for his proof of the Poincaré conjecture. They are right to ask me: my life experience was very similar to Perelman's.
I went to a high school for children gifted in math. I was extremely successful in competitions. I got my gold medal at IMO and went to college without entrance exams. I received my undergraduate and graduate degrees in one of the best math academic centers in Soviet Russia. Perelman traveled a similar path.
Without ever having met Perelman, I can suggest two explanations of why he might reject the money.
First explanation. To have it publicly known that you have suddenly come into money is very dangerous in Russia. Perelman's life expectancy would have dropped immediately after accepting the million dollars. Russians that have tons of money either hide their wealth or build steel doors way before they make their first million. In addition to being a life hazard, money attracts a lot of bother. He would have been chased by all types of acquaintances asking for help or suggesting marriage proposals.
Second explanation. We grew up in a communist culture where money was scorned and math was idolized. The goal of research was research. Proving the conjecture was the prize itself. In his mind, receiving the award money might diminish the value of what he did. I understand this way of thinking, but I am personally too practical to follow such feelings and would accept the prize.
My first explanation has a flaw. Though valid, it doesn't explain why he rejected the Fields medal. So I reached for the book abour Perelman, Perfect Rigor: A Genius and the Mathematical Breakthrough of the Century by Masha Gessen. I like Gessen's explanation of why he rejected the Fields medal:
His objection to the Fields Medal, though never stated as clearly, seemed to have been twofold: first: he no longer considered himself a mathematician and hence could not accept a price intended for the encouragement of midcareer researchers; and second, he wanted no part of ICM, with all the attendant publicity, speeches, ceremony, and king of Spain.
The reasons are specifically related to the medal, so the Clay prize rejection might not be connected to the medal rejection. This argument slightly rehabilitates my first explanation.

I liked the book. It is a tremendous undertaking — writing about a person who doesn't want to talk to anyone. After reading it, I have one more possible explanation of his refusal of the prize.
Perelman is a loner. One of the closest people to him was his math Olympiad coach. The coaches tend to understand the solutions on the spot, mostly because they already know them. If in his mind Perelman expected all mathematicians to be like his coach, then he might have expected a parade in his honor the day after he solved the conjecture. Instead, he got silence and attempts to steal the prize from him.
Can you imagine doing the century's best math work without receiving congratulations for many years? The majority of mathematicians waited for the judgment of the experts, as did Perelman. The experts were busy and much slower than Perelman expected. The conjecture was extremely difficult, and it was a high-profile situation — after all, $1 million was attached to its solution. So the experts were very cautious in their pronouncements.
Finally, instead of congratulating Grigory, they said that the proof seemed to be correct and that they had not yet found any mistakes. If like Perelman, I was certain of my proof, I would have found this a painfully under-whelming conclusion.
Perelman expected to feel proud, but instead he probably felt unappreciated and attacked. Instead of the parade he may have hoped for, he had to wait for a long time, only to face disappointment and frustration. This reminds me of an old joke:
A genie is trapped in a lantern at the bottom of the sea. He vows, "I will give one million dollars to the person who frees me." One thousand years pass. He changes his vow, "I will give any amount of money to the one who frees me." Another thousand years pass. He ups the ante, "I will give any amount of money and two more wishes to the person who frees me." Another thousand years pass. He promises, "I will kill the one who frees me."
Third explanation. Perelman was profoundly disappointed in the math community. Unlike the genie, Perelman didn't want to kill anyone, but he did want to express his disillusionment. Perhaps that is why he rejected a million dollars.

Do you like challenging puzzles? Are you tired of sudoku? Here's your chance to try your hand at puzzles that are designed for world puzzle championships.
I've already done the homework for you — and it turned out to be more complicated than I anticipated. The world puzzle federation has a website, but unfortunately they are lazy or secretive. It is difficult to find puzzles there. A few puzzles are available in the World Puzzle Federation Newsletters.
Since I am stubborn, I spent a lot of time looking for championship puzzles. I found them in books. Here is the list I compiled so far. If you too are interested in high-level puzzles, this ought to make your search a lot easier. The book titles are confusing, so I added a description of what's in them.
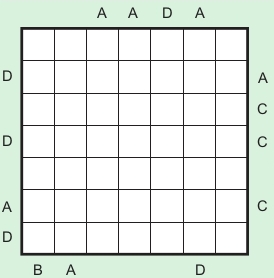
One of my favorite puzzle types is Easy as ABC. You have to fill one of A, B, C, and D in each row and column. The letters outside the grid indicate which letter you see first from that direction. Here is one from the 2011 newsletter:
* * *
Engraved on a mathematician's tombstone: "Q.E.D."
* * *
—You act very brave on the Internet. But could you repeat this looking into my eyes?
—Sure. Send me your picture.
* * *
—Your birthday?
—December 26th.
—What year?
—Every year.
* * *
Teacher: "How much do we get if we cut eight into two halves?"
Student: "Two threes, if we cut vertically; and two zeros, if we cut horizontally."
Two girls. One is older and more experienced. The other is younger and more naive. Which of these two girls will the unnamed male narrator choose? What a great plot for a math book.
I am talking about Hiroshi Yuki's book Math Girls. The plot allows the author to discuss math on different levels. Miruka's math is more advanced and mysterious. Tetra's math is simpler and more transparent.
The book starts discussing sequences and patterns. Can you guess the pattern behind the sequence: 1, 2, 3, 4, 6, 9, 8, 12, 18, 27, …? Can you explain how the beginning of this sequence might be very deceptive?
For the answer, you can read the book, which also discusses tons of fun topics: prime numbers, sum of divisors, absolute values, rotations and oscillations, De Moivre's formula, generating functions, arithmetic and geometric means, differential and difference operators, Catalan numbers, infinite series, harmonic numbers, zeta function, Taylor series, partitions, and more.
I usually do not like math fiction, but this is more math than fiction. It's quite superior to most other math books I've read, for it shows the unity of mathematics. It allows the readers to discover connections among different parts of mathematics, and it accomplishes this in a very thrilling way. Frankly, more thrilling than the romantic sections.
The fictional element brings an additional value to the book. The author uses dialogue to discuss points that are usually skipped in regular text books. The two girls give the narrator an opportunity to explore math on different levels: to talk about heavy stuff with Miruka and to provide explanations with Tetra.
I expected to be more interested in the sections dealing with advanced math. But the book is so well-written that the simpler things were a lot of fun, too. For example, I never before noticed that the column notation for n choose k is exactly the same as for a 2d vector with coordinates n and k. And I will never ever shout "zero" because the exclamation makes it "one".

I have a problem with my binocular vision. The muscles that are responsible for moving my eyes outwards are very weak, much weaker than the muscles that move my eyes inwards. When I am very tired, I can't focus on people or things that are far away. I start seeing doubled monsters with extra eyes and noses.
Luckily, instead of looking scary, the monsters look familiar. In fact, they look exactly like Picasso's portraits. I bet Picasso had problems with his eye muscles.
More than ten years ago I went through a process of psychotherapy which, although very painful, was extremely successful. When I tell my friends about this, they are interested in knowing what can be gained through psychotherapy, so here's my story.
I was living in Princeton, NJ, and I was very tired all the time. My primary care doctor told me that I was depressed and needed to do psychotherapy. A friend of mine recommended Dr. Ella Friedman. During my first visit Ella told me that I block my negative emotions. I protested. All my life I truly tried to be honest with myself. She insisted. I had nothing to lose because I had to solve the problem of my constant exhaustion and I had no other potential solutions. Besides, I liked her very much. So I decided to play along and started my search looking for negative emotions.
For some time I tried to convince Ella that if my best friend broke my favorite mug I wouldn't get angry with her. Ella tried to convince me otherwise. She pushed me back in time to the source of my beliefs and feelings. After several months of therapy, I discovered that I had a strong underlying belief that for my mother to love me, I must be a good girl who is always fair. Since my friend who broke the mug didn't do it on purpose, I wasn't allowed to be angry with her. I repressed all my angry feelings.
It took a lot of time for Dr. Friedman to rewire me and persuade me that my negative emotions do not mean that I am a bad girl. My actions define my goodness, not my emotions. I resisted. She had already convinced me that I might have negative emotions, but I didn't want to look at them. The power forcing me to block my emotions was the threat that my mother would withdraw her love if I wasn't a good girl. Dr. Friedman converted me. I started to believe her and continued more vigorously searching for my hidden emotions. Finally one day I collapsed in the shower. I actually felt my blocked emotions flooding me.
Negative emotions protect us. If someone treats you badly you need to be able to recognize it and get away from the danger. Because I didn't see my emotions I stayed in situations, like toxic relationships, that caused me great pain, without realizing it.
My psychotherapy didn't stop then. We started working on how to understand my emotions and how to process them. Now when someone is talking to me, I listen not only with my ears, but also with my gut. Suppose someone tells me, "I am so glad to see you," but I feel a strange tightness in my stomach. I start wondering what the tightness is about, and usually can figure it out. For the first time I was able to hear my gut and it was more illuminating than what I was hearing with my ears. All my life I processed information as text. Now the sentence "I am so glad to see you" has many different meanings.
The therapy changed my life. It feels as if I added a new sense to my palette of senses. I feel as if I was color blind for many years and at last I can see every color. Now that I've learned to recognize my pain, I can do something about it. I am so much happier today than I ever was before. While my friends may not have consciously recognized the big change in me, they have stopped calling me clueless and now often come to me for advice.
Did this solve my problem of tiredness? When Ella Friedman told me that I was no longer depressed, I still felt tired. I started investigating it further. It turns out that the depression was a result of the tiredness, not the other way around. It seems that I have a sleeping disorder and an iron problem.
SEAHOP created a practice puzzle, called "Making Connections," that includes me. It seems I am making connections.
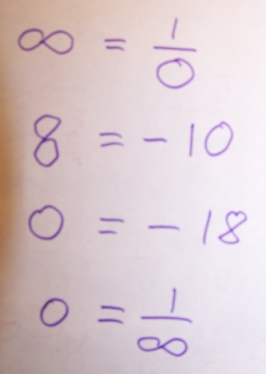
I found a strange piece of paper in an old pile. I believe that it is a visual proof of the following statement:
If ∞ = 1/0, then 0 = 1/∞.
Proof. Assume ∞ = 1/0. Rotate each side of the equation counterclockwise 90 degrees. We get 8 = −10. Subtract 8, getting 0 = −18. Then rotate both parts back: 0 = 1/∞. QED.
I recently posted a short article on plagiarism. Did you notice that not a word of it was mine?
Baron Münchhausen is famous for his tall tales. My co-author Konstantin Knop wants to rehabilitate him and so invents problems where the Baron is proven to be truthful from the start. We already wrote a paper about one such problem. Here is a new problem by Konstantin:
Kostya has a black box, such that if you put in exactly 3 coins of distinct weights, the box will expose the coin of median weight. The Baron gave Kostya 5 coins of distinct weights and told him which coin has the median weight. Can Kostya check that the Baron is right, using the box not more than 3 times?
Actually, Konstantin designed a more complicated problem that was given at the Euler Olympiad, 2012 in Russia.
Let n be a fixed integer. Kostya has a black box, such that if you put in exactly 2n+1 coins of distinct weights, the box will expose the coin of median weight. The Baron gave Kostya 4n+1 coins of distinct weights and told him which coin has the median weight. Can Kostya check that the Baron is right, using the box not more than n+2 times?
Note that Kostya can't just put 4n+1 coins in the box. The box accepts exactly 2n+1 coins. The problem that I started with is for n = 1. Even such a simple variation was a lot of fun for me to solve. So, have fun.
Once upon a time there was a land where the only antidote to a poison was a stronger poison, which needed to be the next drink after the first poison. In this land, a malevolent dragon challenges the country's wise king to a duel. The king has no choice but to accept.
By bribing the judges, the dragon succeeds in establishing the following rules of the duel: Each dueler brings a full cup. First they must drink half of their opponent's cup and then they must drink half of their own cup.
The dragon wanted these rules because he is able to fly to a volcano, where the strongest poison in the country is located. The king doesn't have the dragon's abilities, so there is no way he can get the strongest poison. The dragon is confident of winning because he will bring the stronger poison.
The only advantage the king has is that the dragon is dumb and straightforward. The king correctly predicts what the dragon will do. How can the king kill the dragon and survive?
There is an array containing all the integers from 1 to n in some order, except that one integer is missing. Suggest an efficient algorithm for finding the missing number.
A friend gave me the problem above as I was driving him from the airport. He had just been at a job interview where they gave him two problems. This one can be solved in linear time and constant space.
But my friend was really excited by the next one:
There is an array containing all the integers from 1 to n in some order, except that one integer is missing and another is duplicated. Suggest an efficient algorithm for finding both numbers.
My friend found an algorithm that also works in linear time and constant space. However, the interviewer didn't know that solution. The interviewer expected an algorithm that works in n log n time.
The company claims that they are looking for the smartest people in the world, and my friend had presented them with an impressive solution to the problem. Despite his excitement, I predicted that they would not hire him. Guess who was right?
I reacted like this because of my own story. Many years ago I was interviewing for a company that also wanted the smartest people in the world. At the interview, the guy gave me a list of problems, but said that he didn't expect me to solve all of them — just a few. The problems were so difficult that he wanted to sit with me and read them together to make sure that I understood them.
The problems were Olympiad style, which is my forte. While we were reading them, I solved half of them. During the next hour I solved the rest. The interviewer was stunned. He told me of an additional problem that he and his colleagues had been trying to solve for a long time and couldn't. He asked me to try. I solved that one as well. Guess what? I wasn't hired. Hence, my reaction to my friend's interview.
The good news: I still remember the problem they couldn't solve:
A car is on a circular road that has several gas stations. The gas stations are running low on gas and the total amount of gas available at the stations and in the car is exactly enough for the car to drive around the road once. Is it true that there is a place on the road where the car can start driving, stopping to refuel at each station, so that the car completes a full circle without running out of gas? Assume that the car's tank is large enough not to present a limitation.

Sid Dhawan was one of our RSI 2011 math students. He was studying interlocking polyominoes under the mentorship of Zachary Abel.
A set of polyominoes is interlocked if no subset can be moved far away from the rest. It was known that polyominoes that are built from four or fewer squares do not interlock. The project of Dhawan and his mentor was to investigate the interlockedness of larger polyominoes. And they totally delivered.
They quickly proved that you can interlock polyominoes with eight or more squares. Then they proved that pentominoes can't interlock. This left them with a gray area: what happens with polyominoes with six or seven squares? After drawing many beautiful pictures, they finally found the structure presented in our accompanying image. The system consists of 12 hexominoes and 5 pentominoes, and it is rigid. You cannot move a thing. That means that hexominoes can be interlocked and thus the gray area was resolved.
You can find the proofs and the details in their paper "Complexity of Interlocking Polyominoes". As you can guess by the title, the paper also discusses complexity. The authors proved that determining interlockedness of a a system that includes hexominoes or larger polyominoes is PSPACE hard.
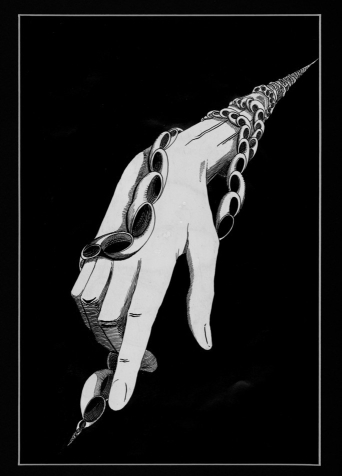
The Fomenko drawing on the left is from the original Russian edition of Homotopic Topology by Fuks, Fomenko and Gutenmacher. Dmitry Fuchs signed this book for me after my success in the USSR Math Olympiad when I was in the 9th grade. For many years I didn't know what the picture meant and was mystified by it. Now the book has been republished with explanations and is available in English at a non-affordable price. You can find this picture and many other Fomenko drawings in his book called Mathematical Impressions, which is affordable, although the comments accompanying the illustrations are confusing. So I have my own explanation for the meaning of this illustration.

The bracelet is made out of shells. Each shell is a hollow cone whose vertex is glued to a point on the rim of the cone's opening, thus giving each hollow cone its own handle. In a part of another drawing (at left), Fomenko shows how the bracelet is built by an army of tiny slaves. First they build the shells and then they connect them together.
How do they connect the shells to each other? The rim of the next shell is glued to the handle of the previous shell. Let me remind you that a straight line connecting a point on the rim to the vertex of a cone is called a generatrix. Imagine a generatrix that connects a vertex of a cone to the point on the rim to which this vertex is glued. This generatrix becomes a circle in a shell, which I call the handle circle. So the rim of the next shell is glued to the handle circle of the previous shell.
Now consider the fundamental group of a shell. The rim can be contracted to the handle circle. Moreover, the cone itself can be contracted to the handle circle. If we glue several shells together, the result is contractible to the handle circle of the last shell.
Now let's go back to the bracelet. The shells become smaller in both directions and end in two points. The front end point is more interesting topologically than the one in back. Every point other than the front end has a contractible neighborhood, while the front end point does not. Or in scientific terms: The bracelet gives an example of a space with a point at which the space is "1-lc" but with no open neighborhoods on which every (Cech) 1-cycle bounds.
My son Sergei invented the following game a couple of years ago. Two people, Alice and Bob, agree on a number, say, four. Alice takes a clean Rubik's cube and secretly makes four moves. Bob gets the resulting cube and has to rotate it to the initial state in not more than four moves. Bob doesn't need to retrace Alice's moves. He just needs to find a short path back, preferably the shortest one. If he is successful, he gets a point and then it is Alice's turn.
If they are experienced at solving Rubik's cube, they can increase the difficulty and play this game with five or six moves.
By the way, how many moves do you need to solve any position on a Rubik's cube if you know the optimal way? The cube is so complicated that people can't always know the optimal way. They think that God can, so they called the diameter of the set of all possible Rubik's cube positions, God's Number. It was recently proven that God's Number is 20. If Alice and Bob can increase the difficulty level to 20, that would mean that they can find the shortest path back to the initial state from any position of the cube, or, in short, that they would master God's algorithm.
One hundred people play the following game. Their names are written on pieces of paper and put into 100 labeled boxes at random. Each box is labeled with a number from 1 to 100 and one name has been placed inside each box. The boxes are placed on a table in a separate room. The players go into the room one by one and each has to open 99 boxes one after another. After each player finishes and leaves the room, the boxes are closed again. The players are not allowed to communicate with each other in any way, although they have been given one day before the event to discuss their strategies. They only win if every one of the one hundred players avoids opening the box with his or her own name. What is the optimal strategy?
Let me first discuss a simpler version of the game. Each player has to open exactly one box and they win if each one of them finds their name. After each player finishes and leaves the room, the boxes are closed again and the room is re-set.
If all of them decide to open box number 42, they are guaranteed to lose. They can try to open random boxes, then they win with probability (1/100)100. Can they use a joint strategy that is better than random?
Yes, they can. Clearly, two people shouldn't open the same box. So on the day before, if each agrees to open a box with a different assigned number, their probability to win is one over 100!. I leave it to my readers to prove that this is the best strategy.
What is the difference between this problem and the original problem? Isn't choosing the last box the same as choosing the first? Aha! When they open 99 boxes they see the names, so they can use this information as part of their strategy.
I hope that this new version is so intriguing that you will start solving this puzzle right away.
* * *
Decimals have a point.
* * *
During the show "Are You Smarter Than a 5th Grader?" the following question was asked:
What is superfluous in the following list: a carrot, an onion, a potato, a Lexus?
A smart 5th grader answered: a carrot, an onion, and a potato.
* * *
If you buy 3 DVDs for the price of 4, you will get one more as a bonus.
* * *
Only yesterday, today was tomorrow.
* * *
By definition, one divided by zero is undefined.
* * *
Finally artificial intelligence has caught up with humans: when filling out electronic forms, many humans need several tries to prove they are not robots.
* * *
Be back in 5 minutes. If I am late, reread this sms.
* * *
— We'll split the money 50-50.
— I want 70.
— Okay, 70-70!
I recently published my new favorite math problem:
A deck of 36 playing cards (four suits of nine cards each) lies in front of a psychic with their faces down. The psychic names the suit of the upper card; after that the card is turned over and shown to him. Then the psychic names the suit of the next card, and so on. The psychic's goal is to guess the suit correctly as many times as possible.
The backs of the cards are asymmetric, so each card can be placed in the deck in two ways, and the psychic can see which way the top card is oriented. The psychic's assistant knows the order of the cards in the deck; he is not allowed to change the order, but he may orient any card in either of the two ways.
Is it possible for the psychic to make arrangements with his assistant in advance, before the latter learns the order of the cards, so as to ensure that the suits of at least (a) 19 cards, (b) 23 cards will be guessed correctly?
If you devise a guessing strategy for another number of cards greater than 19, explain that too.
If the psychic is only allowed to look at the backs of the cards, then the amount of transmitted information is 236, which is the same amount of information as suits for 18 cards. This number of guesses is achievable: the backs of every two cards can clue in the suit of the second card in the pair. This way the psychic can guess the suits of all even-numbered cards in the deck. So the problem is to improve on that. Using the info from the cards that the psychic is permitted to turn over can help too.
The problem is from the book Moscow Mathematical Olympiads, 2000-2005. The book and Russian blog discussions provide many different ideas on how to guess more than half of the deck.
Here is the list of ideas.
Idea 1. Counting cards. If you count cards you will know the suits of the last cards.
Idea 2. Trading. As we discussed before, the psychic can correctly guess the suits of even-numbered cards. By randomly guessing the odd-numbered cards she can correctly guess on average the suits of 4.5 additional cards. Unfortunately, this is not guaranteed. But wait. What if we trade the knowledge of the second card's suit for the majority suit among odd-numbered cards?
Idea 3. Three cards. Suppose we have three cards. Three bits can provide the following knowledge: the majority color, plus the suit of the first and of the second cards in the majority color. Thus, three bits of information will allow the psychic to guess the suits of two cards out of three.
Idea 4. Which card. Suppose the assistant signals the suits of even-numbered cards. With no loss, the psychic can guess the even-numbered card and repeat the same suit for the next card. If this is the plan, the assistant can choose which of the two cards to describe. Which card of the two matches the psychic's guess provides an additional bit of information.
Idea 5. Surprise. Suppose we have a strategy to inform the psychic about some cards. Suppose the assistant deliberately fails on one of the cards. Then the index of this card provides info to the psychic.
I leave it to my readers to use these ideas to find the solution for 19, 23, 24 and maybe even for 26 cards.

Imagine a slice of buttered white bread with a heap of sugar on top. That was my favorite lunch when I was a kid. My mom was working very hard, I was the oldest sister, and this was what I would make for myself almost every day.
Later someone told me that sugar is brain food. I believed that sugar and chocolate helped me do mathematics, so my love for sugar got theoretical support. I finally figured out the source of this love when my first son was born. To teach my son to stop requesting milk at night, my mother pushed me to give him sugar-water instead. At that moment, I realized that I developed my love of sugar with my mother's milk. Or, more precisely, instead of my mother's milk.
Now there is more and more evidence that the love of my life is a mistake. See for example Is Sugar Toxic?. Will I ever be able to break my oldest bad habit, the one I developed before I can remember myself doing it?
This is how my ex-husband Joseph Bernstein used to start his courses in representation theory.
Suppose there is a four-armed dragon on every face of a cube. Each dragon has a bowl of kasha in front of him. Dragons are very greedy, so instead of eating their own kasha they try to steal kasha from their neighbors. Every minute every dragon extends four arms to the neighboring cube's faces and tries to get the kasha from the bowls there. As four arms are fighting for every bowl of kasha, each arm manages to steal one-fourth of what is in the bowl. Thus each dragon steals one-fourth of of the kasha of each of his neighbors, while all of his own kasha is stolen too. Given the initial amounts of kasha in every bowl, what is the asymptotic behavior of the amounts of kasha?
You might ask how this relates to representation theory. First, it relates to linear algebra. We can consider the amounts of kasha as a six-dimensional vector space and the stealing process as a linear operator. As mathematicians, we can easily assume that a negative amount of kasha is allowed.
Now to representation theory. The group of rotations of the cube naturally acts on the 6-dimensional vector space of kashas. And the stealing operator is an intertwining operator of this representation. Now for a spoiler alert: I'm about to finish the solution, so stop here if you want to try it on your own.
The intertwining operator acts as a scalar on irreducible representations of the group. Thus we should decompose our representation into irreducible ones. The group has five irreducible representations with dimensions 1, 1, 2, 3, and 3.
We can decompose the kasha into the following three representations:
We see that asymptotically every dragon will have the same amount of kasha.
Now it is your turn to use this method to solve a similar problem, where there are n dragons sitting on the sides of an n-gon. Each dragon has two arms, and steals half of the kasha from his neighbors. Hey, wait a minute! Why dragons? There are people around the table stealing each other's kasha. But the question is still the same: What is the asymptotic behavior of the amounts of kasha?
Students should use a different strategy for the AIME than for the AMC. So students who are approaching the AIME for the first time need to question the habits they have developed after years of doing multiple choice tests. Here are some suggestions.
Checking. I've noticed that the accuracy level of students who take the AIME for the first time drops significantly. It seems that they are so used to multiple choice questions that they rely on multiple choices as a confirmation that they are right. So when someone solves a problem, they compare their answer to the given choices and if the answer is on the list they assume that the answer must be correct. Their pattern is broken when there are no choices. So they arrive at an answer and since there is no way to check it against choices, they just submit it. Because of this lack of confirmation, checking their answer in other ways becomes more important.
Timing.
At the AMC we have 3 minutes per problem. At the AIME — 12. That means the timing strategies need to be different. Indeed, the AMC is so fast-paced that it is reasonable to save time by not reading a problem twice. If you read it, you either solve it or skip it and go on. The student who is not trying to achieve a perfect score can decide in advance not to read those final, highly-difficult problems.
For the AIME it is not expensive, in relative terms of time, to read all the problems. The student can read the problems and choose the most promising ones to start with, knowing that if there is time they can always come back to other problems.
Guessing. Guessing at the AMC is very profitable if you can exclude three choices out of the given five. Guessing for the AIME is a waste of time because the answers are integers between 000 and 999. So the probability of a random guess is one in a thousand. Actually, this is not quite right, because the problem writers are human and it is much easier to write a problem with an answer of 10 than one with an answer of 731. But the AIME designers are trying very hard to make answers that are randomly distributed. So the probability of a random guess is not one in a thousand, but it is very close. You can improve your chances by an intelligent guess. For example, you might notice that the answer must be divisible by 10. But guessing is still a waste of time. Thinking about a problem for two minutes in order to increase the probability of a correct guess to one in a 100 means that your expected gain is 1/200 points per minute. Which is usually much less than the gain for checking your answers. You can play the guessing game if you have exhausted your other options.
What saddens me is that the students who are not trained in checking use their first guess to make their life choices. But this is a subject for a separate discussion.

I have already written about how American math competition are illogically structured, for the early rounds do not prepare students for the later rounds. The first time mathletes encounter proofs is in the third level, USAMO. How can they prepare for problems with proofs? My suggestion is to look East. All rounds of Russian math Olympiads — from the local to the regional to the national — are structured in the same way: they have a few problems that require proofs. This is similar to the USAMO. At the national All-Russian Olympiad, the difficulty level is the same as USAMO, while the regionals are easier. That makes the problems from the regionals an excellent way to practice for the USAMO. The best regional Olympiad in Russia is the Moscow Olympiad. Here is the problem from the 1995 Moscow Olympiad:
We start with four identical right triangles. In one move we can cut one of the triangles along the altitude perpendicular to the hypotenuse into two triangles. Prove that, after any number of moves, there are two identical triangles among the whole lot.
This style of problems is very different from those you find in the AMC and the AIME. The answer is not a number; rather, the problem requires proofs and inventiveness, and guessing cannot help.
Here is another problem from the 2002 Olympiad. In this particular case, the problem cannot be adapted for multiple choice:
The tangents of a triangle's angles are positive integers. What are possible values for these tangents?

The problems are taken from two books: Moscow Mathematical Olympiads, 1993-1999, and Moscow Mathematical Olympiads, 2000-2005. I love these books and the problems they present from past Moscow Olympiads. The solutions are nicely written and the books often contain alternative solutions, extended discussion, and interesting remarks. In addition, some problems are indexed by topics, which is very useful for teachers like me. But the best thing about these books are the problems themselves. Look at the following gem from 2004, which can be used as a magic trick or an idea for a research paper:
A deck of 36 playing cards (four suits of nine cards each) lies in front of a psychic with their faces down. The psychic names the suit of the upper card; after that the card is turned over and shown to him. Then the psychic names the suit of the next card, and so on. The psychic's goal is to guess the suit correctly as many times as possible.
The backs of the cards are asymmetric, so each card can be placed in the deck in two ways, and the psychic can see which way the top card is oriented. The psychic's assistant knows the order of the cards in the deck; he is not allowed to change the order, but he may orient any card in either of the two ways.
Is it possible for the psychic to make arrangements with his assistant in advance, before the latter learns the order of the cards, so as to ensure that the suits of at least (a) 19 cards, (b) 23 cards will be guessed correctly?
If you devise a guessing strategy for another number of cards greater than 19, explain that too.
Do you remember how to divide three apples among four people? Make apple sauce, of course. In the following two puzzles you are not allowed to cut apples. Here is an old riddle:
There are four apples in a basket. How can you divide them among four people, so that one apple remains in the basket?
Here is a variation from Konstantin Knop's blog:
There are four apples in a basket. How can you divide them among three people, so that no one has more than the others and one apple remains in the basket?
Imagine a magician who comes on stage and performs the following magic trick:
He asks someone in the audience to think of a two-digit number, then subtract the sum of its digits. He waves his wand and guesses that the result is divisible by nine. Ta-Da!
This is not magic. This is a theorem. To make it magical we need to disguise the theorem.

First, there are many ways to hide the fact that we subtract the sum of the digits. For example, we can ask to subtract the digits one by one, while chatting in between. It is better to start with subtracting the first digit. Indeed, if we start with subtracting the second digit, the audience might notice that the result is divisible by 10 and start suspecting that some math is involved here. You can be more elaborate in how you achieve the subtraction of the sum of digits. For example, subtract twice the first digit, then the second, then add back the original number divided by 10.
Second, we need to disguise that the result is divisible by 9. A nice way to do this is implemented in the online version of this trick. The website matches the resulting number to a gift that is described on the page in pale letters. Paleness of letters is important as it is difficult to see that the same gift reappears in a pattern. In my work with students I use the picture on the left. At the end I tell them, "Ta-Da! the resulting number is blue." Here is the full sized version of the same picture that you can download.
My students are too smart. They see through me and guess what is going on. Then I ask them the real question, "Why do I have some cells with question marks and other symbols?" To give you a hint, I can tell you that the symbols are there for the same reason some blue numbers are not divisible by 9.
We got this problem from Rados Radoicic:
A 7 by 7 board is covered with 38 dominoes such that each covers exactly 2 squares of the board. Prove that it is possible to remove one domino so that the remaining 37 still cover the board.
Let us call a domino covering of an n by n board saturated if the removal of any domino leaves an uncovered square. Let d(n) be the number of dominoes in the largest saturated covering of an n by n board. Rados' problem asks us to prove that d(7) < 38.
Let's begin with smaller boards. First we prove that d(2) = 2. Suppose that 3 dominoes are placed on a 2 × 2 board. Let us rotate the board so that at least two of the dominoes are horizontal. If they coincide, then we can remove one of them. If not, they completely cover the board and we can remove the third one. Similarly, you can check all the cases and show that d(3) = 6.
Now consider a saturated domino covering of an n × n board. We can view the dominoes as vertices of a graph, joining two if they share a cell of the board. No domino can share both cells with other dominoes, or we could remove it. Hence, each domino contains at most one shared cell. This means that all the dominoes in a connected component of the graph must overlap on a single shared cell. Hence, the only possible connected components must have the following shapes:
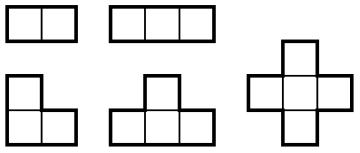
The largest shape in the picture is the X-pentomino. We can describe the other shapes as fragments of an X-pentomino, where the center and at least one more cell is intact. We call these shapes fragments.
A saturated covering by D dominoes corresponds to a decomposition of the n × n board into F fragments. Note that a fragment with k cells is made from k − 1 dominoes. Summing over the dominoes gives: D = n2 − F. Thus, in order to make D as large as possible, we should make F as small as possible. Let f(n) be the minimal number of fragments that are required to cover an n by n board without overlap. Then d(n) = n2 − f(n).
Consider the line graph of the n by n board. The vertices of the line graph correspond to cells in the original board and the edges connect vertices corresponding to neighboring cells. Notice that in the line graph our fragments become all star graphs formed by spokes coming out from a single central node. Thus a decomposition of a rectangular board into fragments corresponds to a covering of its line graph by star graphs. Consider an independent set in the line graph. The smallest independent set has the same number of elements as the smallest number of stars that can cover the graph. This number is called a domination number.
Now let's present a theorem connecting domino coverings with X-pentomino coverings.
Theorem. f(n) equals the smallest number of X-pentominoes that can cover an n by n board allowing overlaps and tiles that poke outside, which is the same as the domination number of the corresponding line graph.
The proof of this theorem and the solution to the original puzzle is available in our paper: "Saturated Domino Coverings." The paper also contains other theorems and discussions of other boards, not to mention a lot of pictures.
The practical applications of star graph coverings are well-known and widely discussed. We predict a similar future for saturated domino coverings and its practical applications, two examples of which follow:
First, imagine a party host arranging a plate of cookies. The cookies must cover the whole plate, but to prevent the kids sneaking a bite before the party, the cookies need to be placed so that removal of just one cookie is bound to expose a chink of plate. This means the cookies must form a saturated covering of the plate. Of course the generous host will want to use a maximal saturated covering.
For the second application, beam yourself to an art museum to consider the guards. Each guard sits on a chair in a doorway, from where it is possible to watch a pair of adjacent rooms. All rooms have to be observed. It would be a mistake to have a redundant guard, that is, one who can be removed without compromising any room. Such a guard might feel demotivated and then who knows what might happen. This means that a placement of guards must be a saturated domino covering of the museum. To keep the guards' Union happy, we need to use a maximal saturated covering.
We would welcome your own ideas for applications of saturated coverings.
Several years ago my son Sergei started a new movement: Sergeism. Followers of this philosophy seek to maximize Sergei's happiness. Since Sergei's happiness involves everyone being happy, becoming happy is a consequential goal of his followers.
Let me explain why this might be a perfect religion for many people, not the least myself. My parents didn't teach me to love myself. They taught me to sacrifice myself and put other peoples' interests ahead of my own. After reading tons of books and spending hours in therapy, I've learned to love myself — well, somewhat. But the truth is, I still feel guilty when I pamper myself. Sergeism eliminates this guilt. I can freely invest in my happiness as a committed member of this movement.
I became a Sergeist when I lost all hope of losing weight. I realized that my own health wasn't a strong enough motivation. But I'm always glad to skip a cookie in tribute to Sergeism. If, like me, you put others ahead of yourself and never find the time to exercise or the will to refuse deserts, join me. Become a Sergeist and lose weight for Sergei.
I recently posted an essay Binary Bulls without Cows with the following puzzle:
The test Victor is taking consists of n "true" or "false" questions. In the beginning, Victor doesn't know any answers, but he is allowed to take the same test several times. After completing the test each time, Victor gets his score — that is, the number of his correct answers. Victor uses the opportunity to re-try the test to figure out all the correct answers. We denote by a(n) the smallest numbers of times Victor needs to take the test to guarantee that he can figure out all the answers. Prove that a(30) ≤ 24, and a(8) ≤ 6.
There are two different types of strategies Victor can use to succeed. First, after each attempt he can use each score as feedback to prepare his answers for the next test. Such strategies are called adaptive. The other type of strategy is one that is called non-adaptive, and it is one in which he prepares answers for all the tests in advance, not knowing the intermediate scores.
Without loss of generality we can assume that in the first test, Victor answers "true" for all the questions. I will call this the base test.
I would like to describe my proof that a(30) ≤ 24. The inequality implies that on average five questions are resolved in four tries. Suppose we have already proven that a(5) = 4. From this, let us map out the 24 tests that guarantee that Victor will figure out the 30 correct answers.
As I mentioned earlier, the first test is the base test and Victor answers every question "true." For the second test, he changes the first five answers to "false," thus figuring out how many "true" answers are among the first five questions. This is equivalent to having a base test for the first five questions. We can resolve the first five questions in three more tests and proceed to the next group of five questions. We do not need the base test for the last five questions, because we can figure out the number of "true" answers among the last five from knowing the total score and knowing the answers for the previous groups of five. Thus we showed that a(mn) ≤ m a(n). In particular, a(5) = 4 implies a(30) ≤ 24.
Now I need to prove that a(5) = 4. I started with a leap of faith. I assumed that there is a non-adaptive strategy, that is, that Victor can arrange all four tests in advance. The first test is TTTTT, where I use T for "true" and F for "false." Suppose for the next test I change one of the answers, say the first one. If after that I can figure out the remaining four answers in two tries, then that would mean that a(4) = 3. This would imply that a(28) ≤ 21 and, therefore, a(30) ≤ 23. If this were the case, the problem wouldn't have asked me to prove that a(30) ≤ 24. By this meta reasoning I can conclude that a(4) ≠ 3, which is easy to check anyway. From this I deduced that all the other tests should differ from the base test in more than one answer. Changing one of the answers is equivalent to changing four answers, and changing two answers is equivalent to changing three answers. Hence, we can assume that all the other tests contain exactly two "false" answers. Without loss of generality, the second test is FFTTT.
Suppose for the third test, I choose both of my "false" answers from among the last three questions, for example, TTFFT. This third test gives us the exactly the same information as the test TTTTF, but I already explained that having only one "false" answer is a bad idea. Therefore, my next tests should overlap with my previous non-base tests by exactly one "false" answer. The third test, we can conclude, will be FTFTT. Also, there shouldn't be any group of questions that Victor answers the same for every test. Indeed, if one of the answers in the group is "false" and another is "true," Victor will not figure out which one is which. This uniquely identifies the last test as FTTFT.
So, if the four tests work they should be like this: TTTTT, FFTTT, FTFTT, FTTFT. Let me prove that these four tests indeed allow Victor to figure out all the answers. Summing up the results of the last three tests modulo 2, Victor will get the parity of the number of correct answers for the first four questions. As he knows the total number of correct answers, he can deduce the correct answer for the last question. After that he will know the number of correct answers for the first four questions and for every pair of them. I will leave it to my readers to finish the proof.
Knop and Mednikov in their paper proved the following lemma:
If there is a non-adaptive way to figure out a test with n questions by k tries, then there is a non-adaptive way to figure out a test with 2n + k − 1 questions by 2k tries.
Their proof goes like this. Let's divide all questions into three non-overlapping groups A, B, and C that contain n, n, and k − 1 questions correspondingly. By our assumptions there is a non-adaptive way to figure out the answers for A or B using k tries. Let us denote subsets from A that we change to "false" for k − 1 non-base tests as A1, …, Ak-1. Similarly, we denote subsets from B as B1, …, Bk-1.
Our first test is the base test that consists of all "true" answers. For the second test we change the answers to A establishing how many "true" answers are in A. In addition we have k − 1 questions of type Sum: we switch answers to questions in Ai ∪ Bi ∪ Ci; and type Diff: we switch answers to (A ∖ Ai) ∪ Bi. The parity of the sum of "false" answers in A − Ai + Bi and Ai + Bi + Ci is the same as in A plus Ci. But we know A's score from the second test. Hence we can derive Ci. After that we have two equations with two unknowns and can derive the scores of Ai and Bi. From knowing the number of "true" answers in A and C, we can derive the same for B. Knowing A and Ai gives all the answers in A. Similarly for B. QED.
This lemma is powerful enough to answer the original puzzle. Indeed, a(2) = 2 implies a(5) ≤ 4, and a(3) = 3 implies a(8) ≤ 6.
The following variation of a Bulls and Cows problem was given at the Fall 2008 Tournament of the Towns:
A test consists of 30 true or false questions. After the test (answering all 30 questions), Victor gets his score: the number of correct answers. Victor doesn't know any answer, but is allowed to take the same test several times. Can Victor work out a strategy that guarantees that he can figure out all the answers after the 29th attempt? after the 24th attempt?
Let's assume that we have a more general problem. There are n questions, and a(n) is the smallest number of times we need to take the test to guarantee that we can figure out the answers. First we can try all combinations of answers. This way we are guaranteed to know all the answers after 2n attempts. The next idea is to start with a baseline test, for example, to say that all the answers are true. Then we change answers one by one to see if the score goes up or down. After changing n − 1 answers we will know the answers to the first n − 1 questions. Plus we know the total number of true answers, so we know the answers to all the questions. We just showed that a(n) ≤ n.
This is not enough to answer the warm-up question in the problem. We need something more subtle.
Let's talk about the second part of the problem. As we know, 24 = 4 ⋅ 6. So to solve the second part, on average, we need to find five correct answers per four tests. Is it true that a(5) ≤ 4? If so, can we use it to show that a(30) ≤ 24?
The following three cases are the most fun to prove: a(5) = 4, a(8) ≤ 6, and a(30) ≤ 24. Try it!
By the way, K. Knop and L. Mednikov wrote a paper (available in Russian) where they proved that a(n) is not more than the smallest number k such that the total number of ones in the binary expansion of numbers from 1 to k is at least n − 1. Which means they proved that a(30) ≤ 16.

On the left is a puzzle from the 2000 Qualifying Test for USA and Canada teams to compete in the world puzzle championship. A set of all 21 dominoes has been placed in a 7 by 6 rectangular tray. The layout is shown with the pips replaced by numbers and domino edges removed. Draw the edges of the dominoes into the diagram to show how they are positioned.
We would like to discuss the mathematical theory behind this puzzle using a toy example below. Only three dominoes: 1-1, 1-2, 2-2 are positioned on the board and the goal is to reconstruct the positioning:
Let's connect adjacent numbers with segments to show potential dominoes and color the segments according to which domino they represent. The 1-1 edge is colored green, the 1-2 — blue, and the 2-2 — red. Now our puzzle has become a graph, where the numbers are vertices, the segments are edges, and the edges are colored. In this new setting, the goal of the puzzle is to find edges of three different colors so that they do not share vertices.
The next picture represents the line graph of the previous graph. Now the colors of the vertices correspond to different potential dominoes. Vertices are connected if the corresponding dominoes share a cell. In the new setting finding dominoes that do not share a cell is equivalent to finding an independent set. The fact that we need to use all possible dominoes means that we want the most colorful independent set.
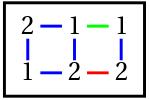
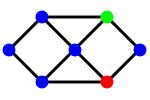
* * *
— If a black cat crosses in front of you and then crosses back, what does it mean? Is your bad luck doubled or canceled?
— Is this a scalar or a vector cat?
— Huh?
— A scalar cat doubles and a vector cat cancels.
* * *
Unbuttered bread, unable to cause the usual harm, tries to fall on the dirtiest spot.
* * *
Chance is a design carefully planned by someone else.
* * *
Wikipedia: I know everything.
Google: I can find anything.
Facebook: I know everyone.
Internet: You are nothing without me.
Electricity: Shut up, jerks.
* * *
Yesterday I bought pills to increase my IQ. Couldn't open the jar.
* * *
Today I opened my desktop's case and finally understood whither my trash is emptied.
I just discovered a Russian Internet Linguistics Olympiad. Even though most linguistics problems are not translatable, this time we are lucky. My favorite problem from this Olympiad is related to chemical elements — their names in Russian have the same logical structure as in English. Keep in mind, the problem doesn't assume any knowledge of chemistry. Here is the problem:
The formulae for chemical elements and their names are given below in mixed order:
C3H8, C4H6, C3H4, C4H8, C7H14, C2H2;
Heptene, Butine, Propane, Butene, Ethine, Propine.
- Match the formulae with their names. Explain your solution.
- Write the names of the elements with the following formulae: C2H4, C2H6, C7H12.
- Write the formulae for the following elements: Propene, Butane.
I have two admirers, Alex and Mike. Alex lives next to my home and Mike lives next to my MIT office. I have a lousy memory, so I invented the following system to guarantee that I see both of my friends and also manage to come to my office from time to time. I have a sign hanging on the inside of my home door that says Office on one side and Alex on the other. When I approach the door, I can see right away where I went last time. So I flip the sign and that tells me where next to go. I have a similar sign inside my office door that tells me to go either to home or to Mike. Every evening I spend with one of my admirers discussing puzzles or having coffee. Late at night I come home to sleep in my own bed. Now let's see what happens if today my home sign shows Office and the office sign shows Mike:
After three days the signs return to their original positions, meaning that the situation is periodic and I will repeat this three-day pattern forever.
Let's get back to reality. I am neither memory-challenged nor addicted to coffee. I invented Alex and Mike to illustrate a rotor-router network. In general my home is called a source: the place where I wake up and start the day. There can only be one source in the network. My admirers are called targets and I can have an infinite number of them. The network needs to be constructed in such a way that I always end up with a friend by the end of the day. There could be many other places that I can visit, other than my office: for example, the library, the gym, opera and so on. These places are other vertices of a network that could be very elaborate. Any place where I go, there is a sign that describes a pattern of where I go from there. The sign is called a rotor.
The patterns at every rotor might be more complicated than a simple sign. Those patterns are called rotor types. My sign is called 12 rotor type as it switches between the first and the second directions at every non-friend place I visit.
The sequence of admirers that I visit is called a hitting sequence and it can be proved that the sequence is eventually periodic. Surprisingly, the stronger result is also true: the hitting sequence is purely periodic.
The simple 12 rotor is universal. That means that given a set of friends and a fancy periodic schedule that designates the order I want to visit them in, I can create a network of my activities where every place has a sign of this type 12 and where I will end up visiting my friends according to my pre-determined periodic schedule.
It is possible to see that not every rotor type is universal. For example, palindromic rotor types generate only palindromic hitting sequences, thus they are not universal. The smallest such example, is rotor type 121. Also, block-repetitive rotor types, like 1122, generate block-repetitive hitting sequences.
It is a difficult and an interesting question to describe universal rotor types. My PRIMES student Xiaoyu He was given a project, suggested by James Propp, to prove or disprove the universality of the 11122 rotor type. This was the smallest rotor type the universality of which was not known. Xiaoyu He proved that 11122 is universal and discovered many other universal rotor types. His calculations support the conjecture that only palindromic or block-repetitive types are not universal. You can find these results and many more in his paper: On the Classification of Universal Rotor-Routers.
My co-author Konstantin Knop wrote a charming book, Weighings and Algorithms: from Puzzles to Problems. The book contains more than one hundred problems. Here are a couple of my favorites that I translated for you:
There is one gold medal, three silver medals and five bronze medals. It is known that one of the medals is fake and weighs less than the corresponding genuine one. Real medals made of the same metal weigh the same and from different metals do not. How can you use a balance scale to find the fake medal in two weighings?
There are 15 coins, out of which not more than seven are fake. All genuine coins weigh the same. Fake coins might not weigh the same, but they differ in weight from genuine coins. Can you find one genuine coin using a balance scale 14 times? Can you do it using fewer weighings?
You might get the impression that the latter problem depends on two parameters. Think about it: It is necessary that the majority of the coins are genuine in order to be able to solve the problem. In fact, the number of weighings depends on just one parameter: the total number of coins. Denote a(n) the optimal number of weighings needed to find a genuine coin out of n coins, where more than half of the coins are genuine. Can you calculate this sequence?
Hint. I can prove that a(n) ≤ A011371(n-1); that is, the optimal number of weighings doesn't exceed n − 1 − (number of ones in the binary expansion of n−1).
We all heard this paradoxical statement:
This statement is false.
Or a variation:
True or False: The correct answer to this question is 'False'.
Recently we received a link to the following puzzle, which is similar to the statement above, but has a cute probabilistic twist:
If you choose an answer to this question at random, what is the chance you will be correct?
- 25%
- 50%
- 60%
- 25%
There are four answers, so you can choose a given answer with probability 25%. But oops, this answer appears twice. Is the correct answer 50%? No, it is not, because there is only one answer 50%. You can see that none of the answers are correct, hence, the answer to the question—the chance to be correct—is 0. Now is the time to introduce our new puzzle:
If you choose an answer to this question at random, what is the chance you will be correct?
- 25%
- 50%
- 0%
- 25%
This fractal was designed by Ross Hilbert and is named "Weathered Steel Weave." You can find many other beautiful pictures in his fractal gallery.
The fractal is based on iterations of the following fractal formula znew = cos(c zold), where the Julia Constant c is equal to −0.364444444444444+0.995555555555556i. To produce the image, you need to start with a complex value of z and iterate it many times using the formula above. The color is chosen based on how close the iteration results are to the border of the unit circle.
I found a new Russian Olympiad for high schools related to universities. I translated my favorite problems from last year's final round. These are the math problems:
8th grade. In a certain family everyone likes their coffee with milk. At breakfast everyone had a full cup of coffee. Given that Alex consumed a quarter of all consumed milk and one sixth of all coffee, how many people are there in the family?
8th grade. How many negative roots does the equation x4 − 5x3 − 4x2 − 7x + 4 = 0 have?
10th grade. Find a real-valued function f(x) that satisfies the following inequalities for any real x and y: f(x) ≤ x and f(x+y) ≤ f(x) + f(y).
I liked the physics problems even more:
8th grade. Winnie-the-Pooh weighs 1 kg. He hangs in the air with density 1.2kg/m3 next to a bee hive. He is holding a rope connected to a balloon. Estimate the smallest possible diameter of the balloon, assuming that this happens on Earth.
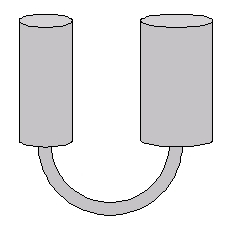
10th grade. Two containers shaped like vertical cylinders are connected by a pipe underneath them. Their heights are the same and they are on the same level. The cross-sectional area of the right container is twice bigger than the left's. The containers are partially filled with water of room temperature. Someone put ice into both containers: three times more ice into the right one than into the left one. After that, the containers are closed hermetically. How will the water level will change after the ice melts completely:
- The levels will not change.
- The level on the left will be higher than on the right.
- The level on the left will be lower than on the right.
- The answer depends on the initial volume of water in the containers.
Once I talked to my friend Michael Plotkin about IQ tests, which we both do not like. Michael suggested that I run an experiment and send a standard IQ question for children to my highly-educated friends. So I sent a mass email asking:
What's common between an apple and an orange?
I believe that the expected answer is that both are fruits.
Less than half of my friends would have passed the IQ test. They gave four types of answer. The largest group chose the expected answer.
The second group related the answer to language. For example, apples and oranges both start with a vowel and they both have the letters A and E in common.
The third group connected the answer to what was on their minds at the time:
And the last group were people who just tried to impress me:
If my friends with high IQs have given so many different answers, I would expect children to do the same. The variety of answers is so big that no particular one should define IQ. By the way, my own well-educated kids' answers are quoted above — and they didn't go with the standard answer. I'm glad they never had IQ tests as children: I'm sure they would never have passed.
I have an idea for a start-up medical insurance company for Massachusetts. My insurance will have an infinite deductible. That means you pay your own bills. The cost of insurance can be very low, say $100 a year, as I do not need to do anything other than to send you a letter confirming that you have medical insurance. People who otherwise will be fined up to $900 for being uninsured will run in droves to buy my insurance.
I have an even better idea. For an extra fee, I will negotiate with doctors so that you will pay the same amount as medical insurance companies pay to them, which is often three times less than you would pay on your own.
Who am I kidding? I am not a business person, I can't build a company. But I am looking to buy the insurance I just described.
I am just wondering:
What is the largest integer consisting of distinct digits such that, in its English pronunciation, all the words start with the same letter?
I continue to wonder:
What is the largest integer consisting of the same digit such that, in its English pronunciation, all the words start with distinct letters?
When you name your child there are many considerations to take into account. For example, you should always check that your kids' initials don't embarrass them. For example, if the Goldsteins want to name their son Paz, because it means golden in Biblical Hebrew, the middle name shouldn't be Isaak, or anything starting with I.
Contemporary culture adds another consideration: how easy would it be to find your child on the Internet? I personally find it extremely convenient to have a rare name, because my fans can find my webpage and blog just by googling me. Parents need to decide whether they want their children to be on the first page of the search engine or hidden very far away when someone googles them.
When I named my son Sergei, I knew that there was another mathematician named Sergei Bernstein. But I didn't think about the Internet. As a result, I confused the world: is my son more than a hundred years old or did Sergei Natanovich Bernstein compete at Putnam?

I decided to see the film The Oxford Murders because I loved the idea of "Frodo" being a graduate student in logic. By Frodo, I mean the actor Elijah Wood, who is very believable as a math student.
At the core of the movie are sequences of numbers and symbols. When the characters started a discussion about how to continue a sequence, I immediately tensed up. Why? Because when people ask what the next element in the sequence is, I get ready to confront them, by explaining that there are many ways to continue a sequence. For example, the sequence — 1, 2, 4 — could be powers of two, or could be Tribonacci numbers, or any of 10,000 sequences that the Online Encyclopedia of Integer Sequences spills out if you plug in 1, 2, 4. That is, if we do not count the infinity of sequences that are not in the Encyclopedia.
To my surprise and relief, the logic Professor, one of the main characters in the movie, explained that there is no unique way to continue a sequence. From that moment on, I relaxed and fell in love with the movie.
The movie is a detective story with a lot of twists and turns. The crimes are related to symbols. The first two symbols are in the picture below. Can you guess the next symbol?
I cannot. There is an irony in the film at this point, because the Professor and the student need to guess the sequence in order to solve the crimes. But the Professor has already explained that there is no unique way to continue. So illogical for a movie about logic.
And what's worse, the sequence of symbols they finally discover doesn't make sense. I guess I fell in love with this movie too quickly.
* * *
— I've noticed that fools are always sure of themselves, while clever people are doubtful.
— No doubt.
* * *
— What happened to your girlfriend, that really cute math student?
— She's no longer my girlfriend. I caught her cheating on me.
— I don't believe that she cheated on you!
— Well, a couple of nights ago I called her, and she told me that she was in bed wrestling with three unknowns.
* * *
A programmer calls the library:
— Can I talk to Kate please?
— She's in the archive.
— Can you unzip her?
* * *
To protect the population from airplane disasters, Congress has ratified an addendum to the law of gravity.
* * * (invented by David Bernstein)
Energy conservation: it's not just a good idea; it's the law.
* * *
— Your computer is such a mess.
— It got a nasty virus.
— And it poured coffee on your keyboard?
* * *
After little Tom learned to count, his father had to start dividing dumplings evenly.
* * *
In spite of the crisis, inflation, and erratic fluctuations of the market, Russian mathematicians promised the president to keep number Pi between 3 and 4 until at least the end of the year.
* * *
A logician rides an elevator. The door opens and someone asks:
— Are you going up or down?
— Yes.
My webpage and my blog generate a lot of emails. I love receiving most of the emails, but if I reply to them, I won't have time to work on my blog. My favorite type of message is one that is full of compliments, with a note that the writer doesn't expect a reply.
I am grateful to people who send me things I requested, like pictures of Russian plates, or some interesting number properties. I apologize that it takes me so long to reply.
The emails that I don't enjoy reading contain amazing elementary proofs of Fermat's last theorem, or any other theorem on the Millennium list, for that matter. I also do not like when my readers ask me for help with their homework.
Like most people, I'm already dealing with spammers who want to enlarge the body parts I do not have or to slim the ones I do have. However, if you do need to send me millions of dollars that I won in your lottery, there is no reason to waste time on email exchanges: you can process them through my "donate" button.
You are welcome to contact me, but ….
I already gave an example of the kinds of problems that were given to Jewish people at the oral entrance exam to the math department of Moscow State University. In fact, I have a whole page with a collection of such problems, called Jewish problems or Coffins. That page was one of the first pages I created when I started my website more than ten years ago.
When my son Alexey was in high school, I asked him to help me type these problems into a file and to recover their solutions from my more than laconic notes, and solve the problems that I didn't have notes for. He did the job, but the file was lying dormant on my computer. Recently I resurrected the file and we prepared some of the solutions for a publication.
The problems that were given during these exams were very different in flavor: some were intentionally ambiguous questions, some were just plain hard, some had impossible premises. In our joint paper "Jewish Problems" we presented problems with a special flavor. These are problems that have a short and "simple" solution, that is nonetheless very difficult to find. This way the math department of MSU was better protected from appeals and complaints.
Try the following problem from our paper:
Find all real functions of real variable F(x) such that for any x and y the following inequality holds: F(x) − F(y) ≤ (x − y)2.
I will give a talk on the subject for UMA at MIT on October 18, at 5pm.
What's "plagiarism"? It's when you take someone else's work and claim it's your own. It's basically STEALING.
Ideas improve. The meaning of words participates in the improvement. Plagiarism is necessary. Progress implies it. It embraces an author's phrase, makes use of his expressions, erases a false idea, and replaces it with the right idea.
Perhaps the Russians have done the right thing, after all, in abolishing copyright. It is well known that conscious and unconscious appropriation, borrowing, adapting, plagiarizing, and plain stealing are variously, and always have been, part and parcel of the process of artistic creation. The attempt to make sense out of copyright reaches its limit in folk song. For here is the illustration par excellence of the law of Plagiarism. The folk song is, by definition and, as far as we can tell, by reality, entirely a product of plagiarism.
If you copy from one author, it's plagiarism. If you copy from two, it's research.
In my essays The Oral Exam and A Math Exam's Hidden Agenda, I gave some examples of math problems that were used during the entrance exams to Moscow State University. The problems were designed to prevent Jewish and other "undesirable" students from studying at the University. My readers might have supposed that an occasional bright student could, by solving all the problems, get in. Here is the story of my dear friend Mikhail (Misha) Lyubich; it shows that being extremely bright was not enough.
Misha passed the first three exams and was facing his last exam: oral physics. He answered all the questions. None of his answers were accepted: all of them were declared wrong. Misha insisted that he was right and requested that the examiners explain themselves. Every time their reply was the same:
This is not a consultation, it's an exam.
Misha failed the exam. The solution to the last problem was a simple picture: a document that seemed to be impossible to deny, so Misha decided that he had grounds for an appeal. The person in charge denied the appeal. When Misha requested an explanation, can you guess the answer?
This is not a consultation, it's an appeal.
Misha ended up studying at Kharkov State University. Now he is a professor at Stony Brook and the director of the Institute for Mathematical Sciences at Stony Brook.
You know that the negation of a true statement is a false statement, and the negation of a false statement is a true statement. You also know that you can negate a sentence by preceding it with "It is not true that …."
Now look at the following statement and its negation, invented by David Bernstein. Which one is true?
How about this pair?
My son Alexey taught me to always plug unused power strips into themselves, so that we can call them "The Rings of Power." These are my Borromean Rings of Power:

Let's call a projection of a body L onto a hyperplane a shadow. Here is a mathematical way to hide behind. An object K can hide behind an object L if in any direction the shadow of K can be moved by a translation to be inside the corresponding shadow of L. If K can hide inside L, then obviously K can hide behind L. Dan Klain drew my interest to the following questions. Is the converse true? If K can hide behind L can it hide inside L? If not, then if K can hide behind L, does it follow that the volume of K is smaller than that of L?
We can answer both questions for 2D bodies by using objects with constant width. Objects with constant width are ones that have the same segment as their shadow in every direction. The two most famous examples are a circle and a Reuleaux triangle:
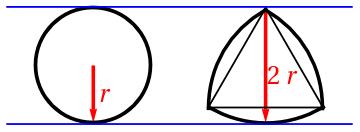
Let's consider a circle and a Reuleaux triangle of the same width. They can hide behind each other. Barbier's Theorem states that all objects of the same constant width have the same perimeter. We all know that given a fixed perimeter, the circle has the largest area. Thus, the circle can hide behind the Reuleaux triangle which has smaller area and, consequently, the circle can't hide inside the Reuleaux triangle. By the way, the Reuleaux triangle has the smallest area of all the objects with the given constant width.
To digress. You might have heard the most famous Microsoft interview question: Why are manhole covers round? Presumably because round manhole covers can't fall into slightly smaller round holes. The same property is true for manhole covers of any shape of constant width. On the picture below (Flickr original) you can see Reuleaux-triangle-shaped covers.

Let's move the dimensions up. Dan's questions become both more difficult and more interesting, because the shadows are not as simple as segments any more.
Before continuing, I need to introduce the concept of "Minkowski sums." Suppose we have two convex bodies in space. Let's designate the origin. Then a body can be represented as a set of vectors from the origin to the points in the body. The Minkowski sum of two bodies are all possible sums of two vectors corresponding to the first body and the second body.
Another way to picture the Minkowski sum is like this: Choose a point in the second body. Then move the second body around by translations so that the chosen point covers the first body. Then the area swept by the second body is the Minkowski sum of both of them.
Suppose we have two convex bodies K and L. Their Minkowski interpolation is the body tK + (1-t)L, where 0 ≤ t ≤ 1 is a scaling coefficient. The picture below made by Christina Chen illustrates the Minkowski interpolation of a triangle and an inverted triangle.
If two bodies can hide behind L, then their Minkowski interpolation can hide behind L for any value of parameter t. In particular if K can hide behind L, then the Minkowski interpolation tK + (1-t)L can hide behind L, for any t.
In my paper co-authored with Christina Chen and Daniel Klain "Volume bounds for shadow covering", we found the following connection between hiding inside and volumes. If L is a simplex, and K can hide behind it, but can't hide inside L, then there exists t such that the Minkowski interpolation tK + (1-t)L has a larger volume than the volume of L.
In the paper we conjecture that the largest volume ratio V(K)/V(L) for a body K that can hide behind another body L is achieved if L is a simplex and K is a Minkowski interpolation of L and an inverted simplex. The 3D object that can hide behind a tetrahedron and has 16% more volume than the tetrahedron was found by Christina Chen. See her picture below.
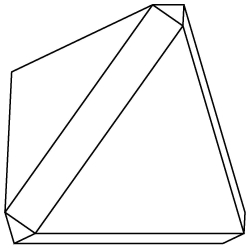
The main result of the paper is a universal constant bound: if K can hide behind L, then V(K) ≤ 2.942 V(L), independent of the dimension of the ambient space.
Question 1. Holodeck. After a long and difficult assignment on an uninhabited planet, Commander Riker went to Holodeck III to unwind. While there he ate three cheeseburgers generated by the holodeck program. Is Commander Riker hungry after he ends the program?
Question 2. Relativity. We know that speed in space is relative, there is no absolute speed. What does Captain Picard mean when he orders a "full stop"?
Question 3. The Replicator. Captain Picard approached a replicator and requested: "Tea, Earl Grey. Hot." The replicator immediately created a glass with hot Earl Grey tea. How much energy would the Enterprise have saved in seven years if they used a dish-washing machine, rather than creating glasses from atoms each time and dissolving them afterwards?
Question 4. Contractions. Commander Data hasn't mastered contractions in English speech. In what year do you think the first program was written to convert formal English into English with contractions?
Question 5. Data. Commander Data is fully functional and absolutely superior to a vibrator. Given that there are more than a thousand people on board the Enterprise, estimate how many times a year on average Data will receive sexual requests.
The next two questions are related to particular episodes.
Question 6. "Up The Long Ladder". Mariposans reproduce by cloning. Why do all the identical sets of clones appear to be the same age? Does it mean that upon the reproduction the clone is the age of the host? If so, they all should be 300 years old.
Mariposans steal sample DNA from Commander Riker and Dr. Pulaski. If Riker and Pulaski didn't destroy their maturing clones what age would those clones be? Would they know how much two plus two is when they awaken? If clones awaken as adults, what is their life span?
Question 7. "Force of Nature". Serova sacrifices herself to save her world from the effects of warp drive, but in doing so, she herself creates the rift that will destroy her world. Explain the logic.
* * *
Logic: if an empty yogurt container is in the sink, a spoon is in the garbage can.
* * *
Logically, a wireless mouse should be called a hamster.
* * *
— I started a new life today.
— You quit smoking and drinking?
— No, I changed my email and Facebook accounts.
* * *
— The reviewer has rejected your paper submitted to our math journal because it doesn't contain any theorems or fomulae or even numbers.
— Wait a minute. Your reviewer is mistaken. There are page numbers on every page.
* * *
A kyboard for sal: only on ky dosn't work.
* * *
My computer always beats me in chess. In revenge, I always beat it in a boxing match.
* * *
— Were your parents married when you were born?
— 50%.
— 50%?
— Yes, my father was married and my mother was not.
* * *
Two programmers are talking:
— I can't turn on my oven.
— What's the error message?
Have you ever been punished for being too good at spider solitaire? I mean, have you ever been stuck because you collected too many suits? Many versions of the game don't allow you to deal from the deck if you have empty columns, nor do they allow you to get back a completed suit. If the number of cards left on the table in the middle of the game is less than ten — the number of columns — you are stuck. I always wondered what the probability is of being stuck. This probability is difficult to calculate because it depends on your strategy. So I invented a boring version of spider solitaire for the sake of creating a math problem. Here it goes:
You start with two full decks of 104 cards. Initially you take 54 cards. At each turn you take all full suits out of your hand. If you have less than ten cards left in your hand, you are stuck. If not, take ten more cards from the leftover deck and continue. What is the probability that you can be stuck during this game?
Let us simplify the game even more by playing the easy level of the boring spider solitaire in which you have only spades. So you have a total of eight full suits of spades. I leave it to my readers to calculate the total probability of being stuck. Here I would like to estimate the easiest case: the probability of being stuck before the last deal.
There are ten cards left in the deck. For you to be stuck, they all should have a different value. The total number of ways to choose ten cards is 104 choose 10. To calculate the number of ways in which these ten cards have different values we need to choose these ten values in 13 choose 10 ways, then multiply by the number of ways each card of a given value can be taken from the deck: 810. The probability is about 0.0117655.
I will leave it to my readers to calculate the probability of being stuck before the last deal at the medium level: when you play two suits, hearts and spades.
No, I will not tell you how many times I played spider solitaire.
Is there a way to put a sequence of numbers to music? The system that comes immediately to mind is to match a number to a particular pitch. The difference between any two neighboring integers is the same, so it is logical to assume that the same tone interval should correspond to the same difference in integers. After we decide which tone interval corresponds to the difference of 1, we need to find our starting point. That is, we need to choose the pitch that corresponds to the number 1. After that, all numbers can be automatically matched to pitches.
After we know the pitches for our numbers, to make it into music we need to decide on the time interval between the notes. The music should be uniquely defined by the sequence, hence the only logical way would be to have a fixed time interval between two consecutive notes.
We see that there are several parameters here: the starting point, the pitch difference corresponding to 1, and the time interval between notes. The Online Encyclopedia of Integer Sequences offers the conversion to music for any sequence. It gives you freedom to set the parameters yourself. The sequences do not sound melodic because mathematical sequences will not necessarily follow rules that comply with a nice melody. Moreover, there are no interesting rhythms because the time interval between the notes is always the same.
One day I received an email from a stranger named Michael Blake. He sent me a link to his video on YouTube called "What Pi Sounds Like." He converted the digits of Pi to music. My stomach hurt while I was listening to his music. My stomach hurts now while I am writing this. He just numbered white keys on the piano from 1 to 9 starting from C. Then he played the digits of Pi. Clearly, Michael is not a mathematician, as he does not seem to know what to do with 0. Luckily for him the first 32 digits of Pi do not contain zero, so Michael played the first several digits over and over. My stomach hurts because he lost the basic math property of digits: the difference between the neighboring digits is the same. In his interpretation the digits that differ by one can have a tone interval of minor or major second in a random order corresponding to his random starting point.
I am not writing this to trash Michael. He is a free man in a free country and can do whatever he wants with the digits of Pi. Oops, I am sorry, he can't do whatever he wants. Michael's video was removed from YouTube due to an odd copyright infringement claim by Lars Erickson, who wrote a symphony using the digits of Pi.
Luckily for my readers Michael's video appears in some other places, for example at the New Scientist channel. As Michael didn't follow the symmetry of numbers and instead replaced the math rules with some music rules, his interpretation of Pi is one of the most melodic I've heard. The more randomly and non-mathematically you interpret digits, the more freedom you have to make a nice piece of music. I will say, however, that Michael's video is nicely done, and I am glad that musicians are promoting Pi.
Other musicians do other strange things. For example, Steven Rochen composed a violin solo based on the digits of Pi. Unlike Michael, he used the same tone interval for progressing from one number to the next, like a mathematician would do. He started with A representing 1 and each subsequent number corresponded to an increase of half a tone. That is, A# is 2 and so on. Like Michael Blake he didn't know what to do with 0 and used it for rest. In addition, when he encountered 10, 11, and 12 as part of the decimal expansion he didn't use them as two digits, but combined them, and used them for F#, G, G# respectively. To him this was the way to cover all possible notes within one octave, but for me, it unfortunately caused another twinge in my stomach.

In August I visited my son Alexey Radul, who currently works at the Hamilton Institute in Maynooth, Ireland. One of the greatest Irish attractions, Broom Bridge, is located there. It's a bridge over the railroad that connects Maynooth and Dublin. One day in 1843, while walking over the bridge, Sir William Rowan Hamilton had a revelation. He understood how the formulae for quaternions should be written. He scratched them into a stone of the bridge. Now the bridge has a plaque commemorating this event. The plaque contains his formulae. I don't remember ever seeing a plaque with math, so naturally I rushed off to make my pilgrimage to Broom Bridge.
Quaternions have very pronounced sentimental value for me, since my first research was related to them. Let's consider a simple graph. We can construct an algebra associated with this graph in the following way. For each vertex we have a generator of the algebra. In addition we have some relations. Each generator squared is equal to −1. If two vertices are connected the corresponding generators anti-commute, and they commute otherwise. The simplest non-commutative algebra associated with a graph corresponds to a graph with two vertices and one edge. If we call the generators i and j, then the we get the relations: i2 = j2 = −1, and ij = −ji. I we denote ij as k, the algebra as a vector space has dimension 4 and a basis: 1, i, j, k. These are exactly the quaternions. In my undergraduate research I studied such algebras related to Dynkin diagrams. Thirty years later I came back to them in my paper Clifford Algebras and Graphs. But I digress.
I was walking on the bridge hoping that like Hamilton I would come up with a new formula. Instead, I was looking around wondering why the Broombridge Station didn't have a ticket office. I already had my ticket, but I was curious how other people would get theirs. I asked a girl standing on the platform where to buy tickets. She said that there is no way to buy tickets there, so she sometimes rides without a ticket. The fine for not having tickets is very high in Ireland, so I expressed my surprised. She told me that she just says that she is from the town of Broombridge if she is asked to present her ticket.
Being a Russian I started scheming: obviously people can save money by buying tickets to Broombridge and continuing without a ticket wherever they need to go. If the tickets are checked, they can claim that they are traveling from Broombridge. Clearly Ireland hasn't been blessed with very many Russians visitors.
Sleeping Beauty participates in the following experiment. On Sunday she is put to sleep, and a fair coin is flipped. Regardless of the result of the coin flip, she is awakened on Monday and is offered a bet. She may pay $550 in which case she will get $1000 if the coin was tails. If the coin was tails, she is put back to sleep with her memory erased, and awakened on Tuesday and given the same bet again. She knows the protocol. Should she take the bet?
As we discussed in our first essay about Sleeping Beauty, she should take the bet. Indeed, if the coin was heads her loss is $550. But if the coin was tails her gain is $900.
To tell you the truth, when Beauty is offered the bet, she dreams: "It would be nice to know the day of the week. If it were Tuesday, then the coin must have been tails and I would gladly take the winning bet."
In our next variation of the riddle her dream comes true.
Every time she is awakened she is offered to buy the knowledge of the day of the week. How much should she be willing to pay to know the day of the week?
Sleeping Beauty participates in the following experiment. On Sunday she is put to sleep, and a fair coin is flipped. Regardless of the result of the coin flip, she is awakened on Monday and asked whether she thinks the coin was heads or not. If the coin was tails, however, then she is put back to sleep with her memory erased, and awakened on Tuesday and asked the same question again. She knows the protocol. She is awakened one morning and instead of the expected questions she is offered a bet. She may pay $600 in which case she will get $1000 if the coin was tails. Should she take the bet?
We know that tripling the triangular number 1 yields the triangular number 3. The figure shows how we can use this fact to conclude that tripling the triangular number 15 yields the triangular number 45.
Using this new fact, can you modify the figure to find even larger examples of tripling triangles?
This post is inspired by the following problem:
Sleeping Beauty participates in the following experiment. On Sunday she is put to sleep, and a fair coin is flipped. Regardless of the result of the coin flip, she is awakened on Monday and asked whether she thinks the coin was heads or not. If the coin was tails, however, then she is put back to sleep with her memory erased, and awakened on Tuesday and asked the same question again. She knows the protocol. She is awakened one morning: What is her probability that the coin was heads?
Some people argue: asleep or awake, the probability of a fair coin being heads is one half, so her probability should be one half.
Other people, including us, argue that those people didn't study conditional probability. On the information of the setup to the problem and the information of having awakened, the three situations "Coin was heads and it is Monday", "Coin was tails and it is Monday", and "Coin was tails and it is Tuesday" are symmetric and therefore equiprobable; thus the probability that the coin was tails is, on this information, two thirds.
So who is right? We are, of course. A good way to visualize probability judgements is to turn them into bets. Suppose each time Beauty wakes up she is offered the following bet: She pays $600 and gets $1000 if the coin was tails. Should she take it? If her probability of the coin being tails were one half, then obviously not; if her probability of the coin being tails were two thirds, obviously yes. So which is it? Consider the situation from her perspective as of Sunday. She can either always take this bet or always refuse it. If she always refuses, she gets nothing. If she always accepts: If the coin turns up heads, she will be asked the question once and will lose $600. If the coin turns up tails, she will be asked the question twice and will gain $800. So on average she will win, so she should take the bet. By this thought experiment, her probability of tails is clearly not one half.
To make matters more interesting, let's try another bet. Suppose she is given the above bet just once, in advance, on Sunday. She pays $600, and she gets paid $1000 on Wednesday if the coin was tails. This has nothing to do with sleeping and awakening. If she takes the bet she loses $600 with probability one half and gains $400 otherwise. So she shouldn't take the bet. Her probability on Sunday that the coin will come up heads is, of course, one half. The point is that just as these two bets are different bets, the sets of information Beauty has on Sunday vs at awakening are different, and lead to different conclusions. On Sunday she knows that the next time she wakes up it will be Monday, but when she then wakes up, she doesn't know that it's Monday.
Parting thought: The phenomenon of predictably losing information leads to the phenomenon of predictably changing one's assessments. Suppose for some reason she decided to take that unprofitable bet on Sunday. When she wakes up during the experiment, should she feel happy or sad? From her perspective during the experiment, the odds of gaining $400 vs losing $600 are two to one, so she should be happy. Given that she knows on Sunday how she will (with complete certainty!) feel about this bet on Monday, should she take it, even given her Sunday self's assessment that it's a bad bet?
If you buy one Mega Millions ticket, your probability of hitting the jackpot is one in 175,000,000. For all practical purposes it is zero. When I give my talk on lotteries, there is always someone in the audience who would argue that "but someone is winning and so can I." The fact that someone is winning depends on the number of people buying tickets. It is difficult to visualize the large number of people buying tickets and the miniscule odds of winning. For example, the probability of you dying from an impact with a meteorite is larger than the odds of winning the jackpot.
I receive a lot of emails from strangers asking me to advertise their websites on my blog. I always check out their websites and I often find them either unrelated to math or boring. That is why I was pleasantly surprised when I was asked to write about a useful website: Understanding Big Numbers. In each post Liam Gray takes a big number and puts it into some perspective. For example, he estimates Mark Zuckerberg's Hourly Wage by dividing Mark's estimated wealth in 2011 by the number of hours Mark might have worked on Facebook. Facebook has existed for 7 years and, assuming 10 hours of work a day every day, we get 25,000 work hours. That is more than half a million dollars an hour.
Imagine someone calls Mark Zuckerberg and asks to talk to him for a minute. Mark wouldn't be out of line to request nine thousand dollars for that. Lucky am I, that I do not need to talk to Mark Zuckerberg.
Here is a game that John Conway popularizes. It is called "Finchley Central," which is a station of the London Underground. The game goes as follows. Alice and Bob take turns naming London Underground stations, in any order. The first person to say "Finchley Central" wins.
Alice, who starts, can just name the station. But then Bob will give her a look. It is not fun to win a game on the first turn. To avoid appearing rude, Alice will not start with "Finchley Central." It would be impolite of Bob to take advantage of Alice's generosity, so he also won't say "Finchley Central." The game might continue like this for a while.
The game has a hidden agenda: winning it after 10 turns will supply many more bragging rights than winning it right away would. We can make this hidden agenda explicit by assigning a value to the honor of continuing the game. For example, suppose every time Alice (or Bob) says a station, she puts one dollar into the pile. The person who says "Finchley Central" first takes all the money from the pile. The implicit goal of the game becomes explicit: you want to say "Finchley Central" right before your opponent says it.
By the way, Finchley Central is not actually a particularly central station — it is the station between Finchley East and Finchley West, serving the relatively small place called Finchley; and is not even under ground. It has the distinction of being one of the oldest still-standing pieces of London Underground physical plant, because plans to rebuild it were interrupted on account of World War II and never resumed. It also has the distinction of having served the home of the guy (an employee of the Underground system) who had the brilliant idea that since the Underground was, indeed, mostly under ground, the right way to map it was topologically, rather than geographically.
Here is another way to model the game. Alice writes an odd number on a piece of paper, and Bob writes an even number. When they compare, the person who wrote a smaller number wins that number of dollars. This version loses the psychological aspect. When you take turns, it is to your advantage to read the non-verbal signs of your opponent to see when s/he is getting ready to drop the bomb.
People play this game in real life. Here are Alice and Bob looking at the last piece of a mouth-watering Tiramisu:
At this point Alice wins with some extra brownie points for being polite.
We can model the honor points differently. We can say you will be the most proud of the game if you name the station write before you opponent is about to do so. Then the model is: everyone writes down their next move; if your move is Finchley Central when your opponent's next move was going to be Finchley Central, then you win.
Here we suggest another game that we call "Reverse Finchley Central." Alice and Bob name London Underground stations in turns and the person who names "Finchley Central" first loses. This game can continue until all the stations are exhausted, if the players are forbidden to repeat them, or it can continue indefinitely otherwise. But this is quite tiresome. The hidden agenda would be to not waste too much time. Clearly the person who values time less will win.
But let us model this game. We want to fix the value of winning. Let us set aside ten dollars for the winner. On their turn, each player puts one dollar into the pile, and as soon as one of the players says "Finchley Central," the other one wins and takes the ten dollars. The pile goes to charity. Alternatively, Alice and Bob can each write a number. The person with the larger number wins the prize, while both have to pay the smaller number to charity.
We play this game with our parents. They nag us to do the dishes. We resist. Then they give up and do the dishes themselves. They lose, but we all pay with our nerves for nagging or being nagged at. Later our parents get their revenge when we have children of our own.
At the 2011 IMO, Lisa Sauermann received yet another gold medal. Now she tops the Hall of Fame of the IMO with four gold medals and one silver medal.
In addition, in 2011 she achieved the absolute best individual result and was the only person with a perfect score. In previous years, there were several girls who tied for first place, but she is the first girl ever to have an absolute rank of 1.
I told you so. In my 2009 essay Is There Hope for a Female Fields Medalist?, I predicted that a girl will soon become an absolute champion of the IMO.
In that essay I draw a parallel between the absolute champion of IMO and a Fields medalist. Indeed, we get one of each per year. Lisa Sauermann is the best math problem solver in her year. Will she grow up to receive a Fields medal? I am not so sure: the medal is still unfriendly to women. Lisa Sauermann is the best math problem solver ever. Will she grow up to be the best mathematician of our century? I wonder.
My e-friend and coauthor, Konstantin Knop, designed the following problem for the 2011 All-Russia Olympiad:
Some cells of a 100 by 100 board have one chip placed on them. We call a cell pretty if it has an even number of neighboring cells with chips. Neighbors are the cells that share a side. Is it possible for exactly one cell to be pretty?
The problem is not easy. Only one person at the Olympiad received full credit for it.
From time to time my female colleagues share stories with me of great unfairness or horrible sexual harassment in the world of mathematics. I can't reciprocate — certainly not on that level.
I do not have any horror stories to tell. Generally I am treated with great respect, at least to my face. In fact, some men have told me that I am the smartest person they ever met.
The stories I want to share are not about harassment. No single incident is a big deal. But when these things happened time after time after time, I realized: this is gender bias.
First story. A guy told me, "Your proof is unbelievably amazing."
What can I say? It is just a compliment. Though I am not sure why the word "unbelievable" was included. Is it difficult to believe that I can produce an amazing proof? I encounter surprise too often to my taste.
Second story. Another guy tells me after I explain a solution to a math problem, "I didn't realize it was so simple."
Actually it wasn't simple. When I explained the solution, it may have seemed simple, but that was because I was able to explain it to him with such clarity. People tend to downgrade their opinion of the problem, rather than upgrade their opinion of my ability. It actually affects my reputation as a mathematician.
Third story. Another guy said to me (and I quote!), "I am so dumb. I tried for a week to write the program that computes these numbers and you did it in one hour. I feel so dumb. I didn't expect myself to be so dumb. Why am I so dumb?"
After the fourth "dumb", I started wondering what it was all about. Many guys try to compete with me. And they hate losing to a woman. It creates a strong motivation for them to discard my brilliance and to explain away my speed, even if they have to claim temporary dumbness.
Fourth story. Someone asked me, "What is the source of the solutions and math ideas in your blog? Can you refer me to the literature?"
I do invest extra effort in citing the sources of the math puzzles I discuss. Everything else — the solutions, the ideas, new definitions, new sequences — I invent myself. I have even started inventing math puzzles. This is my blog. I thought of it myself, I wrote it myself. Has anyone ever asked Terence Tao where he takes the solutions for his blog from?
Unfortunately, this attitude damages my career. When people think that my ideas come from someone else, they do not cite me.
But all these stories however minor happen all the time, not only to me but to all my female colleagues. Gender bias is real. Next time someone tells me how unbelievably amazing my proof is, I will explode.
Recently I stumbled on a cute xkcd comic with the hidden message:
Wikipedia trivia: if you take any article, click on the first link in the article text not in parentheses or italics, and then repeat, you will eventually end up at "Philosophy".
Naturally, I started to experiment. The first thing I tried was mathematics. Here is the path: Mathematics — Quantity — Property — Modern philosophy — Philosophy.
Then I tried physics, which led me to mathematics: Physics — Natural science — Science — Knowledge — Fact — Information — Sequence — Mathematics.
Then I tried Pierre de Fermat, who for some strange reason led to physics first: Pierre de Fermat — French — France — Unitary state — Sovereign state — State — Social sciences — List of academic disciplines — Academia — Community — Living — Life — Objects — Physics.
The natural question is: what about philosophy? Yes, philosophy goes in a cycle: Philosophy — Reason — Rationality — philosophy.
The original comic talks about spark plugs. So I tried that and arrived at physics: Spark plug — Cylinder head — Internal combustion engine — Engine — Machine — Machine (mechanical) — Mechanical system — Power — Physics.
Then I tried to get far away from philosophy and attempted sex, unsuccessfully: Sex — Biology — Natural science. Then I tried dance: Dance — Art — Sense — Physiology — Science.
It is interesting to see how many steps it takes to get to philosophy. Here is the table for the words I tried:
| Word | # Steps |
|---|---|
| Mathematics | 4 |
| Physics | 11 |
| Pierre de Fermat | 24 |
| Spark plug | 19 |
| Sex | 12 |
| Dance | 13 |
Mathematics wins. It thoroughly beats all the other words I tried. For now. Fans of sex might be disappointed by these results and tomorrow they might change the wiki essay about sex to start as:
Modern philosophy considers sex …
Not personally. Someone hacked into my website.
I would like to thank my readers Qiaochu Yuan, Mark Rudkin, "ano" and Paul who alerted me to the problem. Viewers who were using the Google Chrome browser and who tried to visit my website got this message: "This site contains content from howmanyoffers.com, a site known to distribute malware."
It took me some time to figure out what was going on. It appears that on June 19 someone from 89-76-135-50.dynamic.chello.pl hacked into my hosting account and added a script to all my html files and to my blog header. It seems that the script was dormant and wasn't yet doing bad things.
As soon as I grasped what was going on, I replaced all the affected files.
I have had my website for many years without changing my hosting password. Unfortunately, passwords, not dissimilar to humans, have this annoying tendency to become weaker with age. I wasn't paying attention to the declining strength of my password and so I was punished.
Now I have fixed the website and my new password is: qwP35q2054uWiedfj052!@#$%.
Just kidding.
I recently had the following chat with a particular calculator:
It seems odd to me that putting a few more e's down the bottom should result in it thinking there were the same number of extra 10s at the bottom. In fact, I've never seen a calculator answer in this form at all. I'm especially intrigued that the final power of ten seems to be the same in all three cases, so it can't even just be estimating. Do you have any thoughts on what screwy counting could be behind these particular answers?
May the Mass times the Acceleration be with you!
John Conway taught me how to tell time at night. But first I need to explain the notions of the "time in the sky" and the "time in the year."
The clock in the sky. Look at Polaris and treat it as the center of a clock. The up direction corresponds to 12:00. Now we need to find a hand. If you find Polaris the way I do, first you locate the Big Dipper. Then you draw a line through the two stars that are furthest away from the Big Dipper's handle. The line passes through Polaris and is your "hour" hand. Now you can read the time in the sky.
The hand of the clock in the sky makes a full rotation in approximately 24 hours. So if you stare at the sky for a long time, you can calculate the time you spent staring. Keep in mind that the hand in the sky clock is twice as slow as the hour hand, and it turns counter-clockwise. So to figure out how long you're looking into the sky, take the sky-time when you start staring, subtract the sky-time when you stop staring and multiply the result by 2.
To calculate the absolute time, we need to adjust for the day in the year.
The clock in the year. A year has twelve months and a clock has twelve hours. How convenient. You can treat each month as one hour. In addition as a month has about 30 days and an hour has exactly 60 minutes, we should count a day as two minutes. Thus, January 25 is 1:50.
Fact: on March 7th at midnight the clock in the sky shows 12:00. March 7th corresponds to 3:15. So to calculate the solar time you need to add up the time in the sky and the time in the year and multiply it by 2. Then subtracting the result from 6:30, which is twice 3:15, you get the solar time.
You are almost ready. You might need to adjust for daylight savings time or for peculiarities of your time zone.
This time formula is not very precise. But if you are looking into the sky and you do not have your watch or cell phone with you, you probably do not need to know the time precisely.
In my life as a female mathematician I have quite often encountered a mathematician's wife who, despite not knowing me, already hated me. It was clear that it had nothing to do with me personally, so being clueless and naive, I assumed that most men were cheaters and that their wives were extremely insecure and jealous.
Then one day one of the wives decided to be frank about her feelings. It wasn't about cheating, she told me. It was that she felt distant from her husband. He lived in a world of mathematics from which she was excluded. I on the other hand shared this world with him.
It was very sad. It meant that I incurred their jealousy, not because of my sins, but because I am a female mathematician.
Let me tell you another story that helped me realize how all-encompassing this world of mathematics can be for some people. Once I had a very close friend who we will call Jack. I do not want to name him as he is a famous mathematician. Jack told me that the strongest emotions he feels are related to mathematics. He can only feel close to someone if he can share a mathematical discussion with them.
Now I understand the wives better. Husbands like Jack invest so much more in their math world and their colleagues than they do in their home life, that it is not surprising the wives are jealous. Because women mathematicians are scarce, when I appear in their husbands' world, it adds another layer of worry.
Another thing that Jack told me is that he gets such a euphoric feeling when he discovers a new math idea that it is better than any orgasm. Of course, this statement made me question the quality of Jack's orgasms, but in any case, for some mathematicians math is an aphrodisiac.
If math is an aphrodisiac, then tattooing a formula on the lover's body may well enhance the orgasm. I just remembered the movie by Ed Frenkel. But I digress.
If math is an aphrodisiac, then I understand jealous wives even better. Without sex I can give their husbands pleasure they can't.
* * *
I am taking my dog to tweet. He'll check other dog's posts at every pole and will leave his comments.
* * *
Not many people know that 1000 chameleons is a chabillion.
* * *
The Internet paradox: it connects people who are far apart, and disconnects those who are close.
* * *
We bought a cell phone for our TV set. We attached it to the remote control, so that we can call our TV when the remote is lost.
* * *
Mary's mom failed arithmetic. Actually, that is why Mary was born.
* * *
Your call is very important to us. Please, hold. And in the meantime, to protect your health, our customer care team encourages you to drink a glass of water at least every two hours.
* * *
Who is your favorite computer game character?
The stick from Tetris.
* * *
Our new boss invited everyone to bring their keyboards to his office. He kept the employees who had worn letters and laid off the ones with worn arrows.
* * *
My son will be a hacker. He started his career before he was born: he found a flaw in the condom.
I recently stumbled upon some notes (in Russian) of a public lecture given by Vladimir Arnold in 2006. In this lecture Arnold defines a notion of complexity for finite binary strings.
Consider a set of binary strings of length n. Let us first define the Ducci map acting on this set. The result of this operator acting on a string a1a2…an is a string of length n such that its i-th character is |ai − a(i+1)| for i < n, and the n-th character is |an − a1|. We can view this as a difference operator in the field F2, and we consider strings wrapped around. Or we can say that strings are periodic and infinite in both directions.
Let's consider as an example the action of the Ducci map on strings of length 6. Since the Ducci map respects cyclic permutation as well as reflection, I will only check strings up to cyclic permutation and reflection. If I denote the Ducci map as D, then the Ducci operator is determined by its action on the following 13 strings, which represent all 64 strings up to cyclic permutation and reflection: D(000000) = 000000, D(000001) = 000011, D(000011) = 000101, D(000101) = 001111, D(000111) = 001001, D(001001) = 011011, D(001011) = 011101, D(001111) = 010001, D(010101) = 111111, D(010111) = 111101, D(011011) = 101101, D(011111) = 100001, D(111111) = 000000.
Now suppose we take a string and apply the Ducci map several times. Because of the pigeonhole principle, this procedure is eventually periodic. On strings of length 6, there are 4 cycles. One cycle of length 1 consists of the string 000000. One cycle of length 3 consists of the strings 011011, 101101 and 110110. Finally, there are two cycles of length 6: the first one is 000101, 001111, 010001, 110011, 010100, 111100, and the second one is shifted by one character.
We can represent the strings as vertices and the Ducci map as a collection of directed edges between vertices. All 64 vertices corresponding to strings of length 6 generate a graph with 4 connected components, each of which contains a unique cycle.
The Ducci map is similar to a differential operator. Hence, sequences that end up at the point 000000 are similar to polynomials. Arnold decided that polynomials should have lower complexity than other functions. I do not completely agree with that decision; I don't have a good explanation for it. In any case, he proposes the following notion of complexity for such strings.
Strings that end up at cycles of longer length should be considered more complex than strings that end up at cycles with shorter length. Within the connected component, the strings that are further away from the cycle should have greater complexity. Thus the string 000000 has the lowest complexity, followed by the string 111111, as D(111111) = 000000. Next in increasing complexity are the strings 010101 and 101010. At this point the strings that represent polynomials are exhausted and the next more complex strings would be the three strings that form a cycle of length three: 011011, 101101 and 110110. If we assign 000000 a complexity of 1, then we can assign a number representing complexity to any other string. For example, the string 111111 would have complexity 2, and strings 010101 and 101010 would have complexity 3.
I am not completely satisfied with Arnold's notion of complexity. First, as I mentioned before, I think that some high-degree polynomials are so much uglier than other functions that there is no reason to consider them having lower complexity. Second, I want to give a definition of complexity for periodic strings. There is a slight difference between periodic strings and finite strings that are wrapped around. Indeed, the string 110 of length 3 and the string 110110 of length 6 correspond to the same periodic string, but as finite strings it might make sense to think of string 110110 as more complex than string 110. As I want to define complexity for periodic strings, I want the complexity of the periodic strings corresponding to 110 and 110110 to be the same. So this is my definition of complexity for periodic strings: let's call the complexity of the string the number of edges we need to traverse in the Ducci graph until we get to a string we saw before. For example, let us start with string 011010. Arrows represent the Ducci map: 011010 → 101110 → 110011 → 010100 → 111100 → 000101 → 001111 → 010001 → 110011. We saw 110011 before, so the number of edges, and thus the complexity, is 8.
The table below describes the complexity of the binary strings of length 6. The first column shows one string in a class up to a rotation or reflections. The second column shows the number of strings in a class. The next column provides the Ducci map of the given string, followed by the length of the cycle. The last two columns show Arnold's complexity and my complexity.
| String s | # of Strings | D(s) | Length of the end cycle | Arnold's complexity | My complexity |
|---|---|---|---|---|---|
| 000000 | 1 | 000000 | 1 | 1 | 1 |
| 000001 | 6 | 000011 | 6 | 9 | 8 |
| 000011 | 6 | 000101 | 6 | 8 | 7 |
| 000101 | 6 | 001111 | 6 | 7 | 6 |
| 000111 | 6 | 001001 | 3 | 6 | 5 |
| 001001 | 3 | 011011 | 3 | 5 | 4 |
| 001011 | 12 | 011101 | 6 | 9 | 8 |
| 001111 | 6 | 010001 | 6 | 7 | 6 |
| 010101 | 2 | 111111 | 1 | 3 | 3 |
| 010111 | 6 | 111001 | 6 | 8 | 7 |
| 011011 | 3 | 101101 | 3 | 4 | 3 |
| 011111 | 6 | 100001 | 6 | 9 | 8 |
| 111111 | 1 | 000000 | 1 | 2 | 2 |
As you can see, for examples of length six my complexity doesn't differ much from Arnold's complexity, but for longer strings the difference will be more significant. Also, I am pleased to see that the sequence 011010, the one that I called The Random Sequence in one of my previous essays, has the highest complexity.
I know that my definition of complexity is only for periodic sequences. For example, the binary expansion of pi will have a very high complexity, though it can be represented by one Greek letter. But for periodic strings it always gives a number that can be used as a measure of complexity.
I met Leon Vaserstein at a party. What do you think I do at parties? I bug people for their favorite problems, of course. The first riddle Leon gave me is a variation on a famous problem I had already written about. Here's his version:
The hypotenuse of a right triangle is 10 inches, and one of the altitudes is 6 inches. What is the area?
When Leon told me that he had designed some problems for the Soviet Olympiads, naturally I wanted to hear his favorite:
A closed polygonal chain has its vertices on the vertices of a square grid and all the segments are the same length. Prove that the number of segments is even.
* * * A Generic Limerick (submitted by Michael Chepovetsky)
There once was an X from place B,
Who satisfied predicate P,
The X did thing A,
In a specified way,
Resulting in circumstance C.
* * *
I just learned that 4,416,237 people got married in the US in 2010. Not to nitpick, but shouldn't it be an even number?
* * *
We are happy to announce that 100% of Russian citizens are computer-savvy and use the Internet on a regular basis (according to a recent Internet survey).
* * *
Two math teachers had a fight. It seems they couldn't divide something.
* * *
Do you know that if you start counting seconds, once you reach 31,556,926 you discover that you have wasted a whole year?
* * *
What I need after a visit to the hairdresser is a "Save" button.
* * *
— Hello! Is this a fax machine?
— Yes.
* * *
— I am not fat at all! My girlfriend tells me that I have a perfect figure.
— Your girlfriend is a mathematician. For her a perfect figure is a sphere.
* * *
A: Hi, how are you?
B: +
A: Will you come to classes today?
B: -
A: You will be kicked out!
B: =
A: Are you using your calculator to chat?
I wonder what the largest number is that can be represented with one character. Probably 9. How about two characters? Is it 99? What about three or four?
I guess I should define a character. Let's have two separate cases. In the first one you can only use keyboard characters. In the second one you can use any Unicode characters.
I'm awaiting your answers to this.
The last time I talked to John H. Conway, he taught me to walk up the stairs. It's not that I didn't know how to do that, but he reminded me that a nerd's goal in climbing the steps is to establish the number of steps at the end of the flight. Since it is boring to just count the stairs, we're lucky to have John's fun system.
His invention is simple. Your steps should be in a cycle: short, long, long. Long in this case means a double step. Thus, you will cover five stairs in one short-long-long cycle. In addition, you should always start the first cycle on the same foot. Suppose you start on the left foot, then after two cycles you are back on the left foot, having covered ten stairs. While you are walking the stairs in this way, it is clear where you are in the cycle. By the end of the staircase, you will know the number of stairs modulo ten. Usually there are not a lot of stairs in a staircase, so you can easily estimate the total if you know the last digit of that number.
I guess I am not a true nerd. I have lived in my apartment for eight years and have never bothered to count the number of steps. That is, until now. Having climbed my staircase using John's method, I now know that the ominous total is 13. Oh dear.
The Moscow Math Olympiad has a different set of problems for every grade. Students need to write a proof for every problem. These are the 8th grade problems from this year's Olympiad:
Problem 1. There were 6 seemingly identical balls lying at the vertices of the hexagon ABCDEF: at A — with a mass of 1 gram, at B — with a mass of 2 grams, …, at F — with a mass of 6 grams. A hacker switched two balls that were at opposite vertices of the hexagon. There is a balance scale that allows you to say in which pan the weight of the balls is greater. How can you decide which pair of balls was switched, using the scale just once?
Problem 2. Peter was born in the 19th century, while his brother Paul was born in the 20th. Once the brothers met at a party celebrating both birthdays. Peter said, "My age is equal to the sum of the digits of my birth year." "Mine too," replied Paul. By how many years is Paul younger than Peter?
Problem 3. Does there exist a hexagon which can be divided into four congruent triangles by a single line?
Problem 4. Every straight segment of a non-self-intersecting path contains an odd number of sides of cells of a 100 by 100 square grid. Any two consecutive segments are perpendicular to each other. Can the path pass through all the grid vertices inside and on the border of the square?
Problem 5. Denote the midpoints of the non-parallel sides AB and CD of the trapezoid ABCD by M and N respectively. The perpendicular from the point M to the diagonal AC and the perpendicular from the point N to the diagonal BD intersect at the point P. Prove that PA = PD.
Problem 6. Each cell in a square table contains a number. The sum of the two greatest numbers in each row is a, and the sum of the two greatest numbers in each column is b. Prove that a = b.
A mathematician is someone who pauses when asked "How much is two and two?"
Indeed, the answer might be:
I already wrote about the research of my friend Olga Amosova who studied the sickle-cell anemia mutation. She and her colleagues needed to store short fragments of hemoglobin genes for their experiments. All the fragments were identical. They noticed that with time the fragments always broke down in the same place. It was a mystery. When good scientists stumble on a mystery, they start digging.
They found that one of the nucleotides rips off the DNA fragment at the site of the Sickle-cell mutation. That place on the DNA becomes fragile and later breaks down. These sites need to be repaired. The repair is very error-prone and often leads to a mutation.
When DNA strands are left unattended, they want to pair up. There are four types of nucleotides: A, C, G and T. So mathematically the fragment of DNA is a string in the alphabet A, C, G, T. These nucleotides are matched to each other. When two DNA strands pair up, A on one strand always matches T and C matches G. So it is logical that if there are two complementary DNA pieces on the same fragment, they will find each other and pair up. They form a hydrogen bond. For example, a piece AACGT matches perfectly another piece TTGCA. Suppose a substring of DNA consists of a piece AACGT and somewhere later the reverse of the match: ACGTT. Such a string is called an inverted repeat. The DNA fragment I mentioned contains a string AACGT****ACGTT. Two pieces AACGT and ACGTT are complementary and not too far from each other in space. So it is easy for them to find each other and to bond to form a so-called stem-loop or a hairpin structure. The site of Sickle-cell mutation falls into the loop.
Olga and her colleagues discovered that for some particular loops the orientation in space becomes awkward and one of the nucleotides rips off. Such a rip off is called depurination. In further investigation, Olga found examples of when depurination happens. The first sequence of the pair that will bond later has to have at least five nucleotides and has to end in T. Correspondingly the second part in the pair has to begin with A. In the middle there needs to be four nucleotides GTGG. The first G flies away. Enzymes rush like a first aid squad to repair it and introduce mistakes that lead to mutation and diseases like cancer.
DNA was thought to be simply a passive information storage system, not capable of any action. Now we see that DNA is capable of action. DNA can damage itself. Damage provokes a mutation. For all practical purposes it is self-mutilation. Olga and her colleagues scanned the human genome for other sequences that are capable of self-mutilation. They found that such sequences are overwhelmingly present. They are present in much higher numbers than would be expected statistically. The pieces that are capable of damaging themselves occur 40 times more often than would occur if the nucleotides were distributed randomly. They are especially overrepresented in genes linked to cancer.
Self-damaging shouldn't happen in normal situations. It can be provoked by the environment, for example, the chemistry of the cell. That means, that our cancers are not only in our genes but also in our life-style. There was, for example, a suggestion in a recent NY Times article, Is Sugar Toxic?, that too much sugar in a diet might provoke cancer. If the rate of mutation depends on the environment, we can influence it and prolong our lives.
It is not clear why the ability to self-mutilate survives in the evolutionary process. It is quite possible that if something very bad happens to our planet, we need our genes to be able to mutate very fast in order to adjust to the environment so that humans can survive.
Though I never tried to donate my sperm to a sperm bank, because of my inability to produce it, I know that sperm banks look for people who have ancestors who lived for a very long time. Such sperm is in bigger demand as everyone wants their children to live longer. I wonder if this tendency is a mistake. Global warming is upon us. People with longevity genes might not be flexible enough for their children to survive the changing of the Earth.
As you might have guessed from the title, this essay is about domino tilings.
Suppose a subset of a square grid has area N, and the number of possible domino tilings is T. Let's imagine that each cell is contributing a factor of x tilings to the total independently of the others. Then we get that xN = T. This mental exercise suggests a definition: we call the nth root of T the degree of freedom per square for a given region.
Let's consider a 1 by 2k rectangle. There is exactly one way to tile it with dominoes. So the degree of freedom per square of such a rectangle is 1. Now consider a 2 by k rectangle. It has the same area as before, and we know that there should be more than one tiling. Hence, we expect the degree of freedom to be larger than the one in the previous example. The number of tilings of a 2 by k rectangle is Fk-2, where Fk is kth Fibonacci number. So the degree of freedom for large k will be approximately the square root of the golden ratio, which is about 1.272.
You might expect that squares should give larger degrees of freedom than rectangles of the same area. The degree of freedom for a large square is about 1.3385. You can find more information in the beautiful paper Tilings by Federico Ardila and Richard P. Stanley.
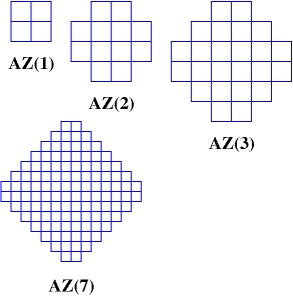
Let's move from rectangles to Aztec diamonds. They are almost like squares but the side of the diamond is aligned with diagonals of the dominoes rather than with their sides. See the sample diamonds in the picture above, which Richard Stanley kindly sent to me for this essay.
It is easier to calculate the degree of freedom for Aztec diamonds than for regular squares. The degree is the fourth root of 2, or 1.1892…. In the picture below created by James Propp's tiling group you can see a random tiling of a large Aztec diamond.
Look at its colors: horizontal dominoes are yellow and blue; vertical ones are red and aquamarine. You might wonder what rule decides which of the horizontal dominoes are yellow and which are blue. I will not tell you the rule; I will just hint that it is simple.

Back to freedom. As you can see from the picture, freedom is highly non-uniform and depends on where you live. Freedom is concentrated inside a circle called the arctic circle, perhaps because the areas outside it are frozen for lack of freedom.
Now I would like to expand the notion of freedom to give each cell its own freedom. For a large Aztec diamond, I will approximate freedom with a function that is one outside the arctic circle and is uniform inside. The Aztec diamond AZ(n) consists of 2n(n+1) squares, shaped like a square with side-length n√2. So the area of the circle is πn2/2. Hence we can calculate the freedom inside the circle as the πth root of 2, which is about 1.247. This number is still much less than the degree of freedom of a cell in a large square.
Jorge Tierno sent me a link to the following puzzle:
There is a certain country where everybody wants to have a son. Therefore, each couple keeps having children until they have a boy, then they stop. What fraction of the children are female?
If we assume that a boy is born with probability 1/2 and children do not die, then every birth will produce a boy with the same probability as a girl, so girls will comprise half of all children.
Now, I wonder why everyone would want a boy? Y-chromosomes are much shorter than X-chromosomes. If a man wants to pass his genes to the next generation, a daughter should be preferable as she keeps more genes from the father. I am a mother of two boys, so my granddaughters will have my X-chromosome while my grandsons will have my ex-husband's Y-chromosome, so to keep my genes in the pool I should be more interested in granddaughters.
But I digress. I started writing this essay because in the original puzzle link the answer was different from mine. Here is how the other argument goes:
Half of all families have zero girls, a quarter have 1/2 girls, 1/8 have 2/3 girls, and so on. If we sum this up the expected ratio of girls to boys is (1/2)0 + (1/4)(1/2) + (1/8)(2/3) + (1/16)(3/4) + ... which adds to 1 − ln 2, which is about 30%.
What's wrong with this solution?
I found this cute problem in the Russian book Sharygin Geometry Olympiad by Zaslavsky, Protasov and Sharygin.
Find numbers p and q that satisfy the equation: x2 + px + q = 0.
The book asks you to find a mistake in the following solution:
By Viète's formulae we get a system of equations p + q = − p, pq = q. Solving the system we get two solutions: p = q = 0 and p = 1, q = −2.
What is wrong with this solution?
I wrote how the written entrance exam was used to keep Jewish students from studying at Moscow State University, but the real brutality happened at the oral exam. Undesirable students were given very difficult problems. Here is a sample "Jewish" problem:
Solve the following equation for real y:
Here is how my compatriots who studied algebra in Soviet high schools would have approached this problem. First, cube it and get a 9th degree equation. Then, try to use the Rational Root Theorem and find that y = 1 is a root. Factoring out y − 1 gives an 8th degree equation too messy to deal with.
The most advanced students would have checked if the polynomial in question had multiple roots by GCDing it with its derivative, but in vain.
We didn't study any other methods. So the students given that problem would have failed it and the exam.
Unfortunately, this problem is impossible to appeal, because it has an elementary solution that any applicant could have understood. It goes like this:
Let us introduce a new variable: x = (y3 + 1)/2. Now we need to solve a system of equations:
This system has a symmetry which we can exploit. The graphs of the functions x = (y3 + 1)/2 and y = (x3 + 1)/2 are reflections of each other across the line x = y. As both functions are increasing, the solution to the system of equations should lie on the line x = y. Hence, we need to solve the cubic y = (y3 + 1)/2, one of whose roots we already know.
Now I offer you another problem without telling you the solution:
Four points on a plane used to belong to four different sides of a square. Reconstruct the square by compass and straightedge.
Recently I asked my readers to look at the 1976 written math exam that was given to applicants wishing to study at the math department of Moscow State University. Now it's time to reveal the hidden agenda. My readers noticed that problems 1, 2, and 3 were relatively simple, problem 4 was very hard, and problem 5 was extremely hard. It seems unfair and strange that problems of such different difficulty were worth the same. It is also suspicious that the difficult problems had no opportunity for partial credit. As a result of these characteristics of the exam, almost every applicant would get 3 points, the lowest passing score. The same situation persisted for many years in a row. Why would the best place to study math in Soviet Russia not differentiate the math abilities of its applicants?
In those years the math department of Moscow State University was infamous for its antisemitism and its efforts to exclude all Jewish students from the University. The strange structure of the exam accomplished three objectives toward that goal.
1. Protect the fast track. There was a fast track for students with a gold medal from their high school who got 5 points on the written exam. The structure of the exam guaranteed that very few students could solve all 5 problems. If by chance a Jewish student solved all 5 problems, it was not much work to find some minor stylistic mistake and not count the solution.
2. Avoid raising suspicion at the next exams. The second math entrance exam was oral. At such an exam different students would talk one-on-one with professors and would have to answer different questions. It was much easier to arrange difficult questions for undesirable students and fail all the Jewish students during the oral exam than during the written exam. But if many students with perfect scores on the written exam had failed the oral exam, it might have raised a lot of questions.
3. Protect appeals. Despite these gigantic efforts, there were cases when Jewish students with a failing score of 2 points were able to appeal and earn the minimum passing score of 3. If undesirable students managed to appeal all the exams, they would only get a half-passing grade at the end and would not be accepted because the department was allowed to choose from the many students that the exams guaranteed would have half-passing scores.
I have only heard about one faculty member who tried to publicly fight the written exam system. It was Vladimir Arnold, and I will tell the story some other time.
The following problem appeared at the Gillis Math Olympiad organized by the Weizmann Institute:
A foreign government consists of 12 ministers. Each minister has 5 friends and 6 enemies amongst the ministers. Each committee needs 3 ministers. A committee is considered legitimate if all of its members are friends or all of its members are enemies. How many legitimate committees can be formed?
Surprisingly, this problem implies that the answer doesn't depend on how exactly enemies and friends are distributed. This meta thought lets us calculate the answer by choosing an example. Imagine that the government is divided into two factions of six people. Within a faction people are friends, but members of two different factions dislike each other. Legitimate committees can only be formed by choosing all three members from the same faction. The answer is 40.
We would like to show that actually the answer to the problem doesn't depend on the particular configuration of friendships and enmities. For this, we will count illegitimate committees. Every illegitimate committee has exactly two people that have one enemy and one friend in the committee. Let's count all the committees from the point of view of these "mixed" people. Each person participates in exactly 5*6 committees as a mixed person. Multiply by 12 (the number of people), divide by 2 (each committee is counted twice) and you get the total 180. This gives an answer of 40 for the number of legitimate committees without using a particular example.
What interests us is the fact that the number of illegitimate, as well as legitimate, committees is completely defined by the degree distribution of friends. For any set of people and who are either friends or enemies with each other, the number of illegitimate committees can be calculated from the degree distribution of friends in the same way as we did above.
Any graph can be thought of as representing friendships of people, where edges connect friends. This cute puzzle tells us that the sum of the number of 3-cliques and 3-anti-cliques depends only on the degree distribution of the graph.
As a non mathematical comment, the above rule for legitimate committees is not a bad idea. In such a committee there is no reason for two people to gang up on the third one. Besides, if at some point in time all pairs of friends switch to enemies and vice versa, the committees will still be legitimate.
In 1976 I was about to become a student in the math department at Moscow State University. As an IMO team member I was accepted without entrance exams, but all of my other classmates had to take the exams. There were four exams: written math, oral math, physics, and an essay.
The written math exam was the first, and here are the problems. I want my non-Russian readers to see if they notice anything peculiar about this exam. Can you explain what is peculiar, and what might be the hidden agenda?
Problem 1. Solve the equation
Problem 2. Solve the inequality
Problem 3. Consider a right triangle ABC with right angle C. Angle B is 30° and leg CA is equal to 1. Let D be the midpoint of the hypotenuse AB, so that CD is a median. Choose F on the segment BC so that the angle between the hypotenuse and the line DF is 15°. Find the area of CDF. Calculate its numeric value with 0.001 precision.
Problem 4. Three balls, two of which are the same size, are tangent to the plane P, as well as to each other. In addition, the base of a circular cone lies on the plane P, and its axis is perpendicular to the plane. All three balls touch the cone from the outside. Find the angle between a generatrix of the cone and the plane P, given that the triangle formed by the points of tangency of the balls and the plane has one angle equal to 150°.
Problem 5. Let r < s < t be real numbers. If you set y equal to any of the numbers r, s or t in the equation x2 − (9 − y)x + y2 − 9y + 15 = 0, then at least one of the other two numbers will be a root of the resulting quadratic equation. Prove that −1 < r < 1.
Let me describe some background to this exam. Applicants who solve fewer than two problems fail the exam and are immediately rejected. People who solve two or three problems are given 3 points. Four problems earn 4 points, and five problems earn 5 points.
If you still do not see the hidden agenda, here is another clue. People who get 5 points on the first exam and, in addition, have a gold medal from their high school (that means all As) are admitted right after the first exam. For the others, if they do not fail any of the exams, points are summed up with their GPAs to compute their scores. The so-called half-passing score is then calculated. Scores strictly higher than the half-passing score qualify applicants for admission. However, there are too many applicants for the available openings with at least the half-passing score. As a result only some people with exactly the half-passing score are accepted, at the discretion of the department.
Now my readers have enough information to figure out the hidden agenda behind that particular exam.
We worked for several years with RSI where we supervised summer math research projects by high school students. Now, we've started an additional program at MIT's math department called PRIMES, where local high school students do math research during the academic year. In this essay we would like to discuss what makes a good math research project for a high school student.
A doable project. The project should not be believed to be extremely difficult to yield at least results. It is very discouraging for an aspiring mathematician not to produce anything during their first project.
An accessible beginning. The student should be able to start doing something original soon after the start of the project. After all, they don't come to us for coursework, but for research.
Flexibility. It is extremely important to offer them a project that is adjustable; it should go in many directions with many different potential kinds of results. Since we do not know the strength of incoming students in advance, it is useful to have in mind both easier and harder versions of the project.
Motivation. It is important for the project to be well motivated, which means related to other things that have been studied and known to be interesting, to research of other people, etc. Students get more excited when they see that other people are excited about their results.
A computer component. This is not a must for a good project. But modern mathematics involves a lot of computation and young students are better at it than many older professors. Such a project gives young students the opportunity to tackle something more senior people are interested in but might not have enough computer skills to solve. In addition, through computer experiments students get exposed to abstract notions (groups, rings, Lie algebras, representations, etc.) in a more "hands-on" way than when taking standard courses, and as a result are less scared of them.
A learning component. It is always good when a project exposes students to more advanced notions.
The student should like their project. This is very difficult to accomplish when projects are chosen in advance before we meet the students. However, we try to match them to great projects by using the descriptions they give of their interests on their applications. It goes without saying that mentors should like their project too.
Having stated the desired properties of a good project, let us move on to giving examples: bad projects and good projects. We start with a bad one:
Prove that the largest power of 2 that doesn't contain 0 is 286.
The project satisfies only one requirement: it contains a computer component. Otherwise, it doesn't have an accessible beginning. It is not very flexible: if the student succeeds, the long-standing conjecture will be proven; if s/he doesn't, there is not much value in intermediate results. The question is not very interesting. The only motivation is that it has been open for a long time. Also, there is not much to learn. Though, almost any theoretical question can be made flexible. We can start with the question above and change its direction to make it more promising and enticing.
Another bad example is a project where the research happens after the programs are written. This is bad because it is difficult to estimate the programming abilities of incoming students. It doesn't have an accessible beginning and there is no flexibility until the programming part is finished. If the student can't finish the programming quickly, s/he will not have time to look at the results and produce conjectures. For example, almost any project in studying social networks may fall into this category:
Study an acquaintance graph for some epic movies or fiction, for example Star Wars or The Lord of the Rings. In this graph people are vertices and two people are connected by an edge if they know each other. The project is to compare properties of such graphs to known properties of other social networks.
Though the networks in movies are much smaller than other networks that people study, the amount of programming might be substantial. This project can be a good project for a person with a flexible time frame or a person who is sure in advance that there will be enough time for him/her to look at the data.
Now on to an example of a good project. Lynnelle Ye and her mentor, Tirasan Khandhawit, chose to analyze the game of Chomp on graphs during RSI 2009.
Given a graph, on each turn a player can remove an edge or a vertex together with all adjacent edges. The player who doesn't have a move loses. This game was previously solved for complete graphs and forest graphs, so the project was to analyze the game for other types of graphs.
It is clear how to analyze the game for any particular new graph. So that could be a starting point providing an accessible beginning. After that the next step could be to analyze other interesting sets of graphs. The flexibility is guaranteed by the fact that there are many sets of graphs that can be used. In addition, the project entails learning some graph theory and game theory. And the project has a computational component.
Lynnelle Ye successfully implemented this project and provided a complete analysis of complete n-partite graphs for arbitrary n and all bipartite graphs. She also gave partial results for odd-cycle pseudotrees. The paper is available at the arxiv. Not surprisingly, Lynelle got fourth place in the Intel Science Talent Search and second place in the Siemens Competition.
Suppose that we choose all families with two children, such that one of them is a son named Luigi. Given that the probability of a boy to be named Luigi is p, what is the probability that the other child is a son?
Here is a potential "solution." Luigi is a younger brother's name in one of the most popular video games: Super Mario Bros. Probably the parents loved the game and decided to name their first son Mario and the second Luigi. Hence, if one of the children is named Luigi, then he must be a younger son. The second child is certainly an older son named Mario. So, the answer is 1.
The solution above is not mathematical, but it reflects the fact that children's names are highly correlated with each other.
Let's try some mathematical models that describe how the parents might name their children and see what happens. It is common to assume that the names of siblings are chosen independently. In this case the first son (as well as the second son) will be named Luigi with probability p. Therefore, the answer to the puzzle above is (2-p)/(4-p).
The problem with this model is that there is a noticeable probability that the family has two sons, both named Luigi.
As parents usually want to give different names to their children, many researchers suggest the following naming model to avoid naming two children in the same family with the same name. A potential family picks a child's name at random from a distribution list. Children are named independently of each other. Families in which two children are named the same are crossed out from the list of families.
There is a problem with this approach. When we cross out families we may disturb the balance in the family gender distributions. If we assume that boys' and girls' names are different then we will only cross out families with children of the same gender. Thus, the ratio of different-gender families to same-gender families will stop being 1/1. Moreover, it could happen that the number of boy-boy families will differ from the number of girl-girl families.
There are several ways to adjust the model. Suppose there is a probability distribution of names that is used for the first son. If another son is born, the name of the first son is crossed out from the distribution and following that we proportionately adjust the probabilities of all other names for this family. In this model the probability of naming the first son by some name and the second son by the same name changes. For example, the most popular name's probability decreases with consecutive sons, while the least popular name's probability increases.
I like this model, because I think that it reflects real life.
Here is another model, suggested by my son Alexey. Parents give names to their children independently of each other from a given distribution list. If they give the same name to both children the family is crossed-out and replaced with another family with children of the same genders. The advantage of this model is that the first child and the second child are named independently from each other with the same probability distribution. The disadvantage is that the probability distribution of names in the resulting set of families will be different from the probability distribution of names in the original preference list.
I would like my readers to comment on the models and how they change the answer to the original problem.

I am reading the book Eat to Live by Joel Fuhrman. It contains a formula that as a math formula doesn't make any sense. But as an idea, it felt like a revelation. Here it is:
HEALTH = NUTRIENTS/CALORIES
The idea is to choose foods that contain more nutrients per calorie. The formula doesn't make sense for many reasons. Taken to its logical conclusion, the best foods would be vitamins and tea. The formula doesn't provide bounds: it just emphasizes that your calories should be nutritious. However, too few calories — nutritious or not — and you will die. And too many calories — even super nutritious — are still too many calories. In addition the formula doesn't explain how to balance different types of nutrients.
Let's see why it was a revelation. I often crave bananas. I assumed that I need bananas for some reason and my body tells me that. Suppose I really need potassium. As a result I eat a banana, which contains 800 milligrams of potassium and adds 200 calories as a bonus. If I ate spinach instead, I would get the same amount of potassium at a price of only 35 calories.
The book suggests that if I start eating foods that are high in nutrients, I will satisfy my need for particular nutrients, and my cravings will subside. As a result I will not want to eat that much. If I start my day eating spinach, that might eliminate my banana desire.
I've been following an intuitive eating diet. I am trying to listen to my body hoping that my body will tell me what is better for it. It seems that my body sends me signals that are not precise enough. It's not that my body isn't communicating with me, but it is telling me "potassium" and all I hear is "bananas." What I need to do is use my brain to help me decipher what my body really, really wants to tell me.
As Dr. Fuhrman puts it, we are a nation of overfed and malnourished people. But Fuhrman's weight loss plan is too complicated and time-consuming for me, so I designed my own plan based on his ideas:
I will start every meal with vegetables, as they are the most nutritious. I hope that vegetables will provide the nutrients I need. That in turn will make me less hungry by the next meal, at which time I'll take in fewer calories. I will report to my readers whether or not my plan works. I'm off to shop for spinach. Will I ever love it as much as bananas?
The Cookie Monster is a peculiar creature that appeared in The Inquisitive Problem Solver (Vaderlind, Guy & Larson, MAA, P34). Presented with a set of cookie jars, the Cookie Monster will try to empty all the jars with the least number of moves, where a move is to select any subset of the jars and eat the same number of cookies from each jar in the subset.
Even an untalented Cookie Monster would be able to empty n jars in n moves: to fulfill this strategy the Monster can devour all the cookies of one jar at a time. If the Monster is lucky and some jars have the same number of cookies, the Monster can apply the same eating process to all these identical jars. For example, if all the jars have the same number of cookies, the Monster can gulp down all of them in one swoop.
Now, let us limit our discussion to only cases of n non-empty jars that contain distinct numbers of cookies. If indeed all the numbers are distinct, can the Monster finish eating faster than in n moves?
The answer depends on the actual number of cookies in each jar. For example, if the number of cookies in jars are different powers of 2, then even the most talented Monsters can't finish faster than in n steps. Indeed, suppose the largest jar contains 2N cookies. That would be more than the total number of cookies in all the other jars together. Therefore, any strategy has to include a step in which the Monster only takes cookies from the largest jar. The Monster will not jeopardize the strategy if it takes all the cookies from the largest jar in the first move. Applying the induction process, we see that we need at least n steps.
On the other hand, sometimes the Monster can finish the jars faster. If 2k−1 jars contain respectively 1, 2, 3, …, 2k−1 cookies, the Cookie Monster can empty them all in k steps. Here is how. For its first move, the Monster eats 2k-1 cookies from each of the jars containing 2k-1 cookies or more. What remains are 2k-1−1 pairs of identical non-empty jars containing respectively 1, 2, 3, …, 2k-1−1 cookies. The Monster can then continue eating cookies in a similar fashion, finishing in k steps. For instance, for k=3 the sequences of non-empty jars are: 1,2,3,4,5,6,7 → 1,1,2,2,3,3 → 1,1,1,1 → all empty.
Now we would like to prove a theorem that shows that the example above is the lowest limit of moves even for the most gifted Cookie Monsters.
Theorem. If n non-empty jars contain distinct numbers of cookies, the Cookie Monster will need at least ⌈log2(n+1)⌉ steps to empty them all.
Proof. Suppose that n jars contain distinct numbers of cookies and let f(n) be the number of distinct non-empty jars after the first move of the Cookie Monster. We claim that n ≤ 2f(n)+1. Indeed, after the first move, there will be at least n − 1 non-empty jars, but there cannot be three identical non-empty jars. That means, the number of jars plus 1 can't decrease faster than twice each time.
Now here is something our readers can play with. Suppose a sequence of numbers represents the number of cookies in the jars. Which sequences are interesting, that is, which can provide interesting solutions for the Cookie Monster problem?
I read an interesting article on the paradoxes involved in allocating seats for the Congress. The problem arises because of two rules: one congressperson has one vote, and the number of congresspeople per state should be proportional to the population of said state.
These two rules contradict each other, because it is unrealistic to expect to be able to equally divide the populations of different states. Therefore, two different congresspeople from two different states may represent different sizes of population.
Let me explain how seats are divided by using as an example a country with three states: New Nevada (NN), Massecticut (MC) and Califivenia (C5). Suppose the total number of congresspeople is ten. Also suppose the population distribution is such that the states should have the following number of congresspeople: NN — 3.33, MC — 3.34 and C5 — 3.33. As you know states generally do not send a third of a congressperson, so the situation is resolved using the Hamilton method. First, each state gets an integer portion of the seats. In my example, each state gets three seats. Next, if there are seats left they are allocated to states with the largest remainders. In my example, the remainders are 0.33, 0.34 and 0.33. As Massecticut has the largest reminder it gets the last seat.
This is not fair, because now each NN seat represents a larger population portion than each MC seat. Not only is this not fair, but it can also create some strange situations. Suppose there have been population changes for the next redistricting: NN — 3.0, MC — 3.4 and C5 — 3.6. In this case, NN and MC each get 3 seats, while C5 gets the extra seat for a total of 4. Even though MC tried very hard and succeeded in raising their portion of the population, they still lost a seat.
Is there any fair way to allocate seats? George Szpiro in his article suggests adding fractional congresspersons to the House of Representatives. So one state might have three representatives, but one of those has only a quarter of a vote. Thus, the state's voting power becomes 2 1/4.
We can take this idea further. We can use the Hamilton method to decide the number of representatives per state, but give each congressperson a fractional voting power, so the voting power of each state exactly matches the population. This way we lose one of the rules that each congressperson has the same vote. But representation will be exact. In my first example, NN got three seats, when they really needed 3.33. So each congressperson from New Nevada will have 1.11 votes. On the other hand MC got four seats, when they needed 3.34. So each MC representative gets 0.835 votes.
Continuing with this idea, we do not need congresspeople from the same state to have the same power. We can give proportional voting power to a congressperson depending on the population in his/her district.
Or we can go all the way with this idea and lose the districts altogether, so that every congressperson's voting power will be exactly proportionate to the number of citizens who voted for him/her. This way the voting power will reflect the popularity — rather than the size of the district — of each congressperson.
Lionel Levine invented a new hat puzzle.
The sultan decides to torture his hundred wise men again. He has an unlimited supply of red and blue hats. Tomorrow he will pile an infinite, randomly-colored sequence of hats on each wise man's head. Each wise man will be able to see the colors of everyone else's hats, but will not be able to see the colors of his own hats. The wise men are not allowed to pass any information to each other.
At the sultan's signal each has to write a natural number. The sultan will then check the color of the hat that corresponds to that number in the pile of hats. For example, if the wise man writes down "four," the sultan will check the color of the fourth hat in that man's pile. If any of the numbers correspond to a red hat, all the wise men will have their heads chopped off along with their hats. The numbers must correspond to blue hats. What should be their strategy to maximize their chance of survival?
Suppose each wise man writes "one." The first hat in each pile is blue with a probability of one-half. Hence, they will survive as a group with a probability of 1 over 2100. Wise men are so wise that they can do much better than that. Can you figure it out?
Inspired by Lionel, I decided to suggest the following variation:
This time the sultan puts two hats randomly on each wise man's head. Each wise man will see the colors of other people's hats, but not the colors of his own. The men are not allowed to pass any info to each other. At the sultan's signal each has to write the number of blue hats on his head. If they are all correct, all of them survive. If at least one of them is wrong, all of them die. What should be their strategy to maximize their chance of survival?
Suppose there is only one wise man. It is clear that he should write that he has exactly one blue hat. He survives with the probability of one-half. Suppose now that there are two wise men. Each of them can write "one." With this strategy, they will survive with a probability of 1/4. Can they do better than that? What can you suggest if, instead of two, there is any number of wise men?
* * *
Today I saw an ad — "A printer for sale" — handwritten. Hmm.
* * *
What do you call a motherboard on your spouse's computer?
The motherboard-in-law.
In a puzzle book by Mari Berrondo (in Russian), I found the following logic problem:
Alfred, Bertran and Charles are asked about their profession. One of them always lies; another one always tells the truth; and the third one [who I will refer to as a "half-liar"] sometimes lies and sometime tells the truth. Here are their answers:
Bertran: I am a painter, Alfred is a piano-tuner, Charles is a decorator.
Alfred: I am a doctor, Charles is an insurance agent. Concerning Bertran, if you ask him, he will tell you that he is a painter.
Charles: Alfred is a piano-tuner. Bertran is a decorator, and I am an insurance agent.
What is the profession of the half-liar?
The solution in the book is the following. As Alfred is right about what Bertran would say, Alfred can't be a liar. If Alfred is a half-liar then the other two people would give the opposite statements, since one will be a truth-teller and the other a liar. But they both say that Alfred is a piano-tuner, therefore Alfred must be a truth-teller. Hence, Alfred's statement about everyone's profession must be the truth. Now we know that Charles is an insurance agent. As Charles confirms that, thus telling the truth in this instance, we recognize that he must be a half-liar. The answer to the problem is that the half-liar is an insurance agent.
But I have a problem with this problem. You see, a liar can say many things. He can say that he is a conductor, a mathematician, a beekeeper or whatever. So there is no way of knowing what a person who decides to lie can say. Let's just analyze the statement by Alfred: "Concerning Bertran, if you ask him, he will tell you that he is a painter."
If Alfred tells the truth about what Bertran would say, he needs to know for sure that Bertran will say that he is a painter. Hence, Bertran must be a truth-teller and a painter. If Alfred lies, he needs to be sure that Bertran won't say that he is a painter. So Bertran must be either a truth-teller and not a painter, or a liar and a painter. Bertran can't be a half-liar, because a half-liar can say that he is a painter as well as he can say something else, no matter what his real profession.
There is one interesting aspect of this that many people overlook. There are different types of people who are half-liars. In some books half-liars are introduced as people who, before making a statement, flip a coin to decide whether to lie or to tell the truth. Such a person needs to know in advance exactly what other people are saying, in order to construct a statement about what those people might say that corresponds to the coin flip. On the other hand, other types of half-liars exist. One half-liar can say something and then see later whether it is true. If Alfred is a half-liar who doesn't care in advance about the truth of his statement, he can say that Bertran will claim that he is a painter.
I leave it to my readers to finish my analysis and see that the problem doesn't have a solution. To end my essay on a positive note, I decided to slightly change the problem, so that there is no contradiction. In the same setting:
Bertran: I am a painter, Alfred is a piano-tuner, Charles is a decorator.
Alfred: I am a doctor, Charles is an insurance agent. Concerning Bertran, if you ask him, he will tell you that he is not a painter.
Charles: Alfred is a piano-tuner. Bertran is a decorator, and I am an insurance agent.
What is the profession of the half-liar?

The data from annual surveys carried out by the American Mathematical Society shows the same picture year after year: the percentage of females in different categories decreases as the category level rises. For example, here is the data for 2006:
| Category | Percentage of Women |
|---|---|
| Graduating Math Majors | 41 |
| PhDs Granted | 32 |
| Fresh PhD hires in academic jobs | 27 |
| Full-time Faculty | 27 |
| Full-time tenured or tenure-track faculty | 12 |
The high percentage of female math majors means that a lot of women do like mathematics. Why aren't women becoming professors of mathematics? In the picture to the left, little Sanya fearlessly took her first integral. I hope, even as an adult, she will never be afraid of integrals.
I am one of the organizers of the Women and Mathematics Program at the Institute for Advanced Study at Princeton In 2009 we had a special seminar devoted to discussing this issue. Here is the report of our discussion based on the notes that Rajaa Al Talli took during the meeting.
Many of us felt, for the following three reasons, that the data doesn't represent the full picture.
First, the different stages correspond to women of different ages; thus, the number of tenured faculty should be compared, not to the number of current math majors, but rather to women who majored in math many years ago. The percentage of female PhDs in mathematics has been increasing steadily for the past several years. As a result, we expect an eventual increase in the number of full-time female faculty.
Second, international women mathematicians might be having a great impact on the numbers. Let's examine a hypothetical situation. If many female professors come to the US after completing their studies in other countries, it would be logical to assume that they would raise the numbers. But since the numbers are falling, we might be losing more females than we think. Or, it could be the opposite: international graduate students complete a PhD in mathematics in the USA and then go back to their own countries. In this case we would be losing fewer females to professorships than the numbers seem to suggest. Unfortunately, we can't really say which case is true as we do not know the data on international students and professors.
Third, many women who major in mathematics also have second majors. For example, the women who have a second major in education probably plan to become teachers instead of pursuing an academic career. It would be interesting to find the data comparing women who never meant to have careers in science with those women who left because they were discouraged. If we are losing women from the sciences because they decide not to pursue scientific careers, then at least that is their choice.
It is also worth studying why so few women are interested in careers in mathematics in the first place. Changing our culture or applying peer pressure in a different direction might change the ambitions of a lot of people.
We discussed why the data in the table doesn't represent the full picture. On the other hand, there are many reasons why women who can do mathematics and want to do mathematics might be discouraged from pursuing an academic career:
Our group proposed many solutions to help retain women in mathematics:
At the end of our meeting, everyone accepted Ingrid Daubechies' proposal that we do the following:
Each woman in mathematics should take as her responsibility the improvement of the mathematical environment in which she works. If every woman helps change what's going on in her university or the school where she teaches, that will help solve the problem on the larger scale.
The book How to Drive Your Man Wild in Bed by Graham Masterton has a chapter on how to choose a lover. It highlights red flags for men who need to be approached with caution. There is a whole list of potentially bad signs, including neglecting to shower in the previous week and talking only about himself.
The list of bad features also includes professions to avoid. Can you guess the first profession on the list? OK, I think you should be able to meta-guess given the fact that I am writing about it. Indeed, the list on page 64 starts:
Avoid, on the whole, mathematicians…
I am an expert on NOT avoiding mathematicians: in fact, I've married three of them and dated x number of them. That isn't necessarily because I like mathematicians so much; I just do not meet anyone else.
When I was a student I had a theory that mathematicians are different from physicists. My theory was based on two conferences on mathematical physics I attended in a row. The first one was targeted for mathematicians and the second for physicists. The first one was very quiet, and the second one was all boozing and partying. So I decided that mathematicians are introverts and physicists are extroverts. I was sure then that my second husband chose a wrong field, because he liked booze and parties.
By now, years later, I've met many more mathematicians, and I have to tell you that they are varied. It is impossible and unfair to describe mathematicians as a type. One mathematician even became the star of an erotic movie. I write this essay for girls who are interested in dating mathematicians. I am not talking about math majors here, I am talking about mathematicians who do serious research. Do I have a word of advice?
I do have several words of caution. While they don't apply to all mathematicians, it's worth keeping them in mind.
First, there are many mathematicians who, like my first husband, are very devoted to mathematics. I admire that devotion, but it means that they plan to do mathematics on Saturday nights and prefer to spend vacation at their desks. If they can only fit in one music concert per year, it is not enough for me. Of course, this applies to anyone who is obsessed by his work.
Second, there are mathematicians who believe that they are very smart. Smarter than many other people. They expand their credibility in math to other fields. They start going into biology, politics and relationships with the charisma of an expert, when in fact they do not have a clue what they are talking about.
Third, there are mathematicians who enjoy their math world so much that they do not see much else around them. The jokes are made about this type of mathematician:
What is the difference between an extroverted mathematician and an introverted one? The extroverted one looks at your shoes, rather than at his own shoes.
Yes, I have met a lot of mathematicians like that. Do you think that their wives complain that their husbands do not notice their new haircuts? No. Such triviality is not worth mentioning. Their wives complain that their husbands didn't notice that the furniture was repossessed or that their old cat died and was replaced by a dog. My third husband was like that. At some point in my marriage I discovered that he didn't know the color of my eyes. He didn't know the color of his eyes either. He wasn't color-blind: he was just indifferent. I asked him as a personal favor to learn the color of my eyes by heart and he did. My friend Irene even suggested creating a support group for the wives of such mathematicians.
While you need to watch out for those traits, there are also things I like about mathematicians. Many mathematicians are indeed very smart. That means it is interesting to talk to them. Also, I like when people are driven by something, for it shows a capacity for passion.
Mathematicians are often open and direct. Many mathematicians, like me, have trouble making false statements. I stopped playing —Mafia— because of that. I prefer people who say what they think and do not hold back.
There is a certain innocence among some mathematicians, and that reminds me of the words of the Mozart character in Pushkin's poetic drama, Mozart and Salieri: —And genius and villainy are two things incompatible, aren't they?— I feel this relates to mathematicians as well. Many mathematicians are so busy understanding mathematics, they are not interested in plotting and playing games.
Would I ever date a mathematician again? Yes, I would.
33 horsemen are riding in the same direction along a circular road. Their speeds are constant and pairwise distinct. There is a single point on the road where the horsemen can pass one another. Can they ride in this fashion for an arbitrarily long time?
The puzzle appeared at the International Tournament of the Towns and at the Moscow Olympiad. Both competitions were held on the same day, which incidentally fell on Pi Day 2010. Just saying: at the Tournament the puzzle was for senior level competitors; at the Moscow Olympiad it was for 8th graders.
Warning: If you want to solve it yourself first, pause now, because here is the solution I propose.
First, consider two horsemen who meet at that single point. The faster horseman passes the slower one and gallops ahead and the slower one canters along. The next meeting point should be at the same place in the circle. Suppose the slower horseman rides n full circles before the next meeting, then the second horseman could not have passed the first in between, so he has to ride n+1 full circles. That means their speeds should have a ratio of (n+1)/n for an integer n. And vice versa, if their speeds have such a ratio, they will meet at the same location on the circle each time. That means that to solve the problem, we need to find 33 different speeds with such ratios.
As all speed ratios are rational numbers, we can scale speeds so that they are relatively prime integers. The condition that two integers have a ratio (n+1)/n is equivalent to the statement that two integers are divisible by their difference. So the equivalent request to the problem is to find a set of 33 positive integers (or prove non-existence), such that every two integers in the set are divisible by their difference.
Let's look at examples with a small number of horsemen. For two riders we can use speeds 1 and 2. For three riders, speeds 2, 3 and 4.
Now the induction step. Suppose that we found positive integer speeds for k horsemen. We can add one more horseman with zero speed who quietly stays at the special point and everyone else passes him. The difference condition is satisfied. We just need to tweak the set of speeds so that the lazy horseman starts moving.
We can see that if we add the least common multiple to every integer in a set of integers such that every two numbers in a pair are divisible by their difference, then the condition stays satisfied. So by induction we can find 33 horsemen. Thus, the answer to the problem is: Yes they can.
Now I would like to apply that procedure from the solution to calculate what kind of speeds we get. If we start with one rider with the speed of 1, we add the second rider with speed 0, then we add 1 to both speeds, getting the solution for two riders: 1 and 2. Now that we have a solution for two riders, we add a third rider with speed 0 then add 2 to every speed, getting the solution for three horsemen: 2, 3 and 4. So the procedure gave us the solutions we already knew for two and three horsemen.
If we continue this, we'll get speeds 12, 14, 15 and 16 for four riders. Similarly, 1680, 1692, 1694, 1695, and 1696 for five riders.
We get two interesting new sequences out of this. The sequence of the fastest rider's speed for n horsemen is: 1, 2, 4, 16, 1696. And the sequence of the least common multiples for n−1 riders — which is the same as the lowest speed among n riders — is: 1, 1, 2, 12, 1680, 343319185440.
The solution above provides very large numbers. It is possible to find much smaller solutions. For example for four riders the speeds 6, 8, 9 and 12 will do. For five riders: 40, 45, 48, 50 and 60.
I wonder if my readers can help me calculate the minimal sequences of the fastest and slowest speeds. That is, to find examples where the integer speed for the fastest (slowest) horseman is the smallest possible.
One day we may all face the necessity of hiring a lawyer. If the case is tricky the lawyer must be smart and inventive. I am collecting puzzles to give to a potential lawyer during an interview. The following puzzle is one of them. It was given at the second Euler Olympiad in Russia:
At a local Toyota dealership, you are allowed to exchange brand new cars. You can exchange three Camrys for one Prius and one Avalon, and three Priuses for two Camrys and one Avalon. Assuming an unlimited supply of cars at the dealership, can collector Vasya exchange 700 Camrys for 400 Avalons?
The beauty of this puzzle is that the answer I may find acceptable from a mathematician is not the same as I want from my future lawyer.
Have I intrigued you? Get to work and send me the solutions.
I am sitting in front of my computer and scheming, or, more precisely, scamming. I am inventing scams as a way of raising awareness of how probability theory can be used for deception.
My first scam is my lottery project. Suppose I create and run a private lottery. I will award minor payments to some participants, while promising a grand prize of one hundred million dollars. However, there will be a very small probability that anyone will win the big payout. My plan is to live lavishly on my proceeds, hoping no one ever wins the big ticket.
The beauty of this scheme is that nobody will complain until someone scores the top prize. After all, everyone has been receiving what I promised, and no one realizes my fraud. If nobody wins the big award until I retire, I will have built my life style on deception without having been caught.
Suppose someone wins the hundred million dollars. Oops. I am in big trouble. On the other hand, maybe I can avoid jail time. I could tell the winner that the money is gone and if s/he complains to the police, I will declare bankruptcy and we will all lose. Alternatively, I can suggest a settlement in exchange for silence. For example, we could share future proceeds. Probability theory will help me run this lottery with only a small chance of being exposed.
But even a small chance of failure will cause me too much stress, so I have come up with an idea for another scam. I will write some complicated mathematical formulas with which to persuade everyone that global warming will necessarily produce earthquakes in Boston in the near future. Then I'll open an insurance company and insure everyone against earthquakes. As I really do not expect earthquakes in my lifetime, I can spend the money. I'll just need to keep everyone scared about earthquakes. This time I can be sure that I won't be caught as no one will have a reason to complain. The only danger is that someone will check my formulas and prove that I used mathematics to lie.
Perhaps I need a scam that covers up the lie better. Instead of inventing an impossible catastrophe, I need to insure against a real but rare event. Think Katrina. I collect the money and put aside money for payouts and pocket the rest. But I actually tweak my formulas and put aside less than I should, boosting my bank account. I will be wealthy for many years, until this event happens. I might die rich but if this catastrophe happens while I'm still alive, I'll declare bankruptcy.
Though I was lying to everyone, I might be able to avoid jail time. I might be able to prove that it was an honest mistake. Mathematical models include some subjective parameters; besides, everyone believes that nature is unpredictable. Who would ever know that I rigged my formulas in my favor? I can claim that the theory ended up being more optimistic than reality is. Who could punish me for optimism?
Maybe I can be accused of lying if someone proves that I knew that the optimistic model doesn't quite match the reality. But it is very difficult for the courts to punish a person for a math mistake.
When I started writing this essay, I wanted to write about the financial crisis of 2008. I ended up inventing scams. In a way, I did write about the financial crisis. My scams are simplified versions of what banks and hedge funds did to us. Will we ever see someone punished?
Most movies related to mathematics irritate me because of simplifications. I especially do not like when a movie pretends to be intelligent and then dumbs it down. I recently watched the Spanish movie Fermat's Room, which, as you may guess, annoyed me several times. In spite of that I enjoyed it very much.
The movie opens with people receiving invitations to attend a meeting for geniuses. To qualify for the meeting they need to solve a puzzle. Within ten days, they must guess the order underlying the following sequence: 5, 4, 2, 9, 8, 6, 7, 3, 1. Right away, at the start of the movie, I was already annoyed because of the simplicity of the question. You do not have to be a genius to figure out the order, not to mention how easy it would be to plug this sequence into the Online Encyclopedia of Integer Sequences to find the order in five minutes.
The participants were asked to hide their real names, which felt very strange to me. All famous puzzle solvers compete in puzzle championships and mystery hunts and consequently know each other.
The meeting presumably targets the brightest minds and promises to provide "the greatest enigma." During the meeting they are given seven puzzles to solve. All of them are from children's books and the so-called "greatest enigma" could easily be solved by kids. Though I have to admit that these were among the cutest puzzles I know. For example:
There are three boxes: one with mint sweets, the second with aniseed sweets, and the last with a mixture of the two. The boxes are labeled, but all the labels are wrong. What is the minimum number of sweets you need to taste to correctly re-label all the boxes?
Another of the film's puzzles includes a light bulb in a room and three switches outside, where you have to correctly find the switch that corresponds to the bulb, but you can only enter the room once. In another puzzle you need to get out of prison by deciding which of two doors leads to freedom. You are allowed to ask exactly one question to one of the two guards, one of whom is a truth-teller and the other is a liar.
The other four puzzles are similar to these three I have just described. To mathematicians they are not the greatest enigmas. They are nice material for a children's math club. For non-mathematicians, they may be fascinating. Certainly it's a good thing that such tasteful puzzles are being promoted to a large audience. But they just look ridiculous as "the greatest enigmas."
So what is it about this film that I so enjoyed?
The intensity of the movie comes from the fact that the people are trapped in a room that starts shrinking when they take more than one minute to solve a puzzle.
I well remember another shrinking room from Star Wars: A New Hope. When Princess Leia leads her rescuers to a room, it turns out to be a garbage compactor. The bad guys activate the compactor and two opposite walls start moving in. In contrast, Fermat's room is shrinking in a much more sophisticated way: all four walls are closing in. Each of the walls in the rectangular room is being pressured by an industrial-strength press. The walls in the corners do not crumble, but rather one wall glides along another. I was more puzzled by this shrinking room than I was by the math puzzles. I recommend that you try to figure out how this can be done before seeing the movie or its poster.
However, the best puzzle in the movie is the plot itself. Though I knew all the individual puzzles, what happened in between grabbed me and I couldn't wait to see what would happen next. I saw the movie twice. After the first time, I decided to write this review, so I needed to check it again. I enjoyed it the second time even better than the first time. The second time, I saw how nicely the plot twists were built.
Maybe I shouldn't complain about the simplicity and the familiarity of the puzzles. If they were serious new puzzles I would have started solving them instead of enjoying the movie. The film's weakness might be its strength.
I collect hats puzzles. A puzzle about hats that I hadn't heard before appeared on the Konstantin Knop's blog (in Russian):
The sultan decides to test his hundred wizards. Tomorrow at noon he will randomly put a red or a blue hat — for both of which he has an inexhaustible supply — on every wizard's head. Each wizard will be able to see every hat but his own. The wizards will not be allowed to exchange any kind of information whatsoever. At the sultan's signal, each wizard needs to write down the color of his own hat. Every wizard who guesses wrong will be executed. The wizards have one day to decide on a strategy to maximize the number of survivors. Suggest a strategy for them.
I'll start the discussion with a rather simple idea: Each wizard writes down a color randomly. In this case the expected number of survivors is 50. Actually, if each wizard writes "red", then the expected number of survivors is 50, too. Can you find a better strategy, with a greater expected number of survivors or prove that such a strategy doesn't exist?
As a bonus question, can you suggest a strategy that guarantees 50 survivors?
Now that you've solved that issue, here's my own variation of the problem.
The wizards are all very good friends with each other. They decide that executions are very sad events and they do not wish to witness their friends' deaths. They would rather die themselves. They realize that they will only be happy if all of them survive together. Suggest a strategy that maximizes the probability of them being happy, that is, the probability that all of them will survive.
The following two problems appeared together in Martin Gardner's Scientific American column in 1959.
Mr. Smith has two children. At least one of them is a boy. What is the probability that both children are boys?
Mr. Jones has two children. The older child is a girl. What is the probability that both children are girls?
Many people, including me and Martin Gardner, wrote a lot about Mr. Smith. In his original column Martin Gardner argued that the answer to the first problem is 1/3. Later he wrote a column titled "Probability and Ambiguity," where he corrected himself about Mr. Smith.
… the answer depends on the procedure by which the information "at least one is a boy" is obtained.
This time I would like to ignore Mr. Smith, as I wrote a whole paper about him that is now under consideration for publication at the College Mathematics Journal. I would rather get back to Mr. Jones.
Mr. Jones failed to stir a controversy from the start and was forgotten. Olivier Leguay asked me about Mr. Jones in a private email, reminding me that the answer to the problem about his children also depends on the procedure.
One of the reasons Mr. Jones was forgotten is that for many natural procedures the answer is 1/2. For example, the following procedures will produce an answer of 1/2:
There are many other procedures that lead to the answer 1/2. However, there are many procedures that lead to other answers.
Suppose I know Mr. Jones, and also know that he has two children. I meet Mr. Jones at a mall, and he tells me that he is buying a gift for his older daughter. Most probably I would assume that the other child is a daughter, too. In my experience, people who have a son and a daughter would say that they are buying a gift for "my daughter." Only people with two daughters would bother to specify that they are buying a gift for "my older daughter."
In some sense I didn't forget about Mr. Jones. I wrote about him implicitly in my essay Two Coins Puzzle. His name was Carl and he had two coins instead of two children.
My blog is getting more famous. Now I don't need to look around for nice problems, for my readers often send them to me. In response to my blog about him, Sergey Markelov's Best, Markelov sent me more of his problems. Here is a cute tetrahedron problem that he designed:
Six segments are such that you can make a triangle out of any three of them. Is it true that you can build a tetrahedron out of all six of them?
Another reader, Alexander Shen, sent me a different tetrahedron problem from a competition after reading my post on Problem Design for Multiple Choice Questions:
Imagine the union of a pyramid based on a square whose faces are equilateral triangles and a regular tetrahedron that is glued to one of these faces. How many faces will this figure have?
Shen wrote that the right answer to this problem had been rumored to have a negative correlation with the result of the entire test.
86 is conjectured to be the largest power of 2 not containing a zero. This simply stated conjecture has proven itself to be proof-resistant. Let us see why.
What is the probability that the nth power of two will not have any zeroes? The first and the last digits are non-zeroes; suppose that other digits become zeroes randomly and independently of each other. This supposition allows us to estimate the probability of 2n not having zeroes as (9/10)k-2, where k is the number of digits of 2n. The number of digits can be estimated as n log102. Thus, the probability is about cxn, where c = (10/9)2 ≈ 1.2 and x = (9/10)log102 ≈ 0.97. The expected number of powers of 2 without zeroes starting from the power N is cxN/(1-x) ≈ 40 ⋅ 0.97N.
Let us look at A007377, the sequence of numbers such that their powers of 2 do not contain zeros: 1, 2, 3, 4, 5, 6, 7, 8, 9, 13, 14, 15, 16, 18, 19, 24, 25, 27, 28, 31, 32, 33, 34, 35, 36, 37, 39, 49, 51, 67, 72, 76, 77, 81, 86. Our estimates predicts 32 members of this sequence starting from 6. In fact, the sequence has 30 conjectured members. Similarly, our estimate predicts 2.5 members starting from 86. It is easy to check that the sequence doesn't contain any more numbers below 200 and our estimate predicts 0.07 members after 200. As we continue checking larger numbers and see that they do not belong to the sequence, the probability that the sequence contains more elements vanishes. With time we check more numbers and become more convinced that the conjecture is true. Currently, it has been checked up to the power 4.6 ⋅ 107. The probability of finding something after that is about 1.764342396 ⋅10-633620.
Let us try to approach the conjecture from another angle. Let us check the last K digits of powers of two. As the number of possibilities is finite, these last digits eventually will start cycling. If we can show that all the elements inside the period contain zeroes, then we need to check the finite number of powers of two until this period starts. If we can find such K, we can prove the conjecture.
Let us look at the last two digits of powers of two. The sequence starts as: 01, 02, 04, 08, 16, 32, 64, 28, 56, 12, 24, 48, 96, 92, 84, 68, 36, 72, 44, 88, 76, 52, 04. As we would anticipate, it starts cycling. The cycle length is 20, and 90% of numbers in the cycle don't have zeroes.
Now let's continue to the last three digits. The period length is 100, and 19 of them either start with zero or contain zero. The percentage of elements in the cycle that do not contain zero is 81%.
The cycle length for the last n digits is known. It is 4 ⋅ 5n-1. In particular the cycle length grows by 5 every time. The number of zero-free elements in these cycles form a sequence A181610: 4, 18, 81, 364, 1638, 7371, 33170. If we continue with our supposition that the digits are random, and study the new digits that appear when we move from the cycle of the last n digits to the next cycle of the last n+1 digits, we can expect that 9/10 of those digits will be non-zero. Indeed, if we check the ratio of how many numbers do not contain zero in the next cycle compared to the previous cycle, we get: 4.5, 4.5, 4.49383, 4.5, 4.5, 4.50007. All of these numbers are quite close to our estimation of 4.5. If this trend continues the portion of the numbers in the cycle that don't have zeroes tends to zero; however, the total of such numbers grows exponentially. We can even estimate that the expected growth is 4 ⋅ 4.5n-1. From this estimation, we can derive the conjecture:
Conjecture. For any number N, there exists a power of two such that its last N digits are zero-free.
Indeed, the last N digits of powers of two cycle, and there are an increasing number of members inside that cycle that do not contain zeroes. The corresponding powers of two don't have zeroes among N rightmost digits.
So, how do we combine the two results? First, the expected probability of finding the power of two larger than 86 that doesn't contain zero is minuscule. And second, we most certainly can find a power of two that has as many zeroless digits at the end as we want.
To combine the two results, let us look at the sequences A031140 and A031141. We can deduce from them that for the power 103233492954 the first zero from the right occupies the 250th spot. The total number of digits of that power is 31076377936. So 250 is a tiny portion of the digits.
As time goes by we grow more and more convinced that 86 is the largest power of two without zeroes, but it is not at all clear how we can prove the conjecture or whether it can be proven at all.
My son, Sergei, suggested that I claim that I have a proof of this conjecture, but do not have enough space in the margin to fit my proof in. The probability that I will ever be shamed and disproven is lower than the probability of me winning a billion dollars in the lottery. Though then, if I do win the big bucks, I will still care about being shamed and disproven.
Janet Mertz encouraged me to find IMO girls and compare their careers to that of their teammates. I had always wanted to learn more about the legendary Lida Goncharova — who in 1962 was the first girl to win an IMO gold medal. So I located her, and after an interview, wrote about her. Only 14 years later, in 1976, did the next girl get a gold medal. That was me. I was ranked overall second and had 39 points out of 40.
As I did in the article about Lida, I would like to compare my math career to that of my teammates.
I got my PhD in 1988 and moved to the US in 1990. My postdoc at MIT in 1993 was followed by a postdoc at Bar-Ilan University. In 1996 I got a non-paying visiting position at Princeton University. In 1998 I gave up academia and moved to industry, accepting an offer from Bellcore. There were many reasons for that change: family, financial, geographical, medical and so on.
On the practical level, I had had two children and raising them was my first priority. But there was also a psychological element to this change: my low self-esteem. I believed that I wasn't good enough and wouldn't stand a chance of finding a job in academia. Looking back, I have no regrets about putting my kids first, but I do regret that I wasn't confident enough in my abilities to persist.
I continued working in industry until I resigned in January 2008, due to my feeling that I wasn't doing what I was meant to do: mathematics. Besides, my children were grown, giving me the freedom to leave a job I did not like and return to the work I love. Now I am a struggling freelance mathematician affiliated with MIT. Although my math blog is quite popular and I have been publishing research papers, I am not sure that I will ever be able to find an academic job because of my non-traditional curriculum vitae.
The year 1976 was very successful for the Soviet team. Out of nine gold medals our team took four. My result was the best for our team with 39 points followed by Sergey Finashin and Alexander Goncharov with 37 points and by Nikita Netsvetaev with 34 points.
Alexander Goncharov became a full professor at Brown University in 1999 and now is a full professor at Yale University. His research is in Arithmetic Algebraic Geometry, Teichmuller Theory and Integral Geometry. He has received multiple awards including the 1992 European Math Society prize. Sergey Finashin is very active in the fields of Low Dimensional Topology and Topology of Real Algebraic Varieties. He became a full professor at Middle East Technical University in Ankara, Turkey in 1998. Nikita Netsvetaev is an expert in Differential Topology. He is a professor at Saint Petersburg State University and the Head of the High Geometry Department.
Comparing my story to that of Lida, I already see a pattern emerging. Now I'm curious to hear the stories of other gold-winning women. I believe that the next gold girl, in 1984, was Karin Gröger from the German Democratic Republic. I haven't yet managed to find her, so can my readers help?
I wrote a series of essays about AMC competitions:
This essay is next in the series. Although it is not strictly about AMC, it should be useful during any test when you need to check your answers. There are several important rules which are helpful.
Rule 0. Checking is important. If wrong answers are punished, then correcting a mistake brings more points than solving a new problem. In addition, problems that were solved are often easier than problems yet to be solved, so finding a mistake might be faster than solving a new problem.
Rule 1. Your checking methods must be fast. The tests are generally timed. This means that in order to check your answers, you need to sacrifice your work on the next problem.
Rule 2. Customize how you check according to your strengths and weaknesses. For example, if you tend to jump to conclusions about what the question is going to be, and as a result answer your anticipated question instead of the one that is actually on the test, then when you are checking you should start reading the problem from the question. Or, if you usually make mistakes in geometry problems, you should allocate more time to geometry problems when you are checking. If you never make mistakes in arithmetic problems then you do not need to check those.
Rule 3. Mark problems that might need checking. If you do not have enough time to check all the problems, check only those you are not sure about.
Rule 4. Do not repeat your solution when you check. While solving the problem your brain often creates a pathway from start to finish. If on this pathway your brain decided to believe that two plus two is five, very often during checking, your brain will make the same mistake again. Because of that it is crucial to use other methods for checking than repeating your reasoning. In case you can't find a way to check your answers using a different method and have to repeat your reasoning, you should repeat it in a different order.
This rule is so important, that I am providing some methods to change your brain pathway when you are checking your answers.
Plug in. Plugging in the answer you found is much faster than finding it. Use this method whenever possible. It is perfect for problems like this one below from 2004 AMC10-A:
What is the value of x if |x – 1| = |x – 2|?
Plug in an intermediate result. Sometimes you can't plug in the answer, but you can plug in an intermediate result. In the following problem from 2004 AMC10-B you can plug in the number of nickels and dimes:
Patty has 20 coins consisting of nickels and dimes. If her nickels were dimes and her dimes were nickels, she would have 70 cents more. How much are her coins worth?
Calculate something else related to your answer. For example a negation. Here is a problem from 2004 AMC10-B:
How many two-digit positive integers have at least one 7 as a digit?
If you calculated the answer directly, to check it you may want to calculate the number of two-digit positive integers that do not contain 7.
Create an example. Sometimes you solve a problem by reasoning, but to check it you might create a particular example. Here is a problem from 2001 AMC10:
Let P(n) and S(n) denote the product and the sum, respectively, of the digits of the integer n. For example, P(23) = 6 and S(23) = 5. Suppose N is a two-digit number such that N = P(N) + S(N). What is the units digit of N?
If we denote the tens digit by a and the units digit by b, then N = 10a + b, P(N) = a*b, and S(N) = a + b. We get an equation a(b+1) = 10a, from which the answer is 9. To check the answer we do not need to repeat the reasoning. It is enough to check that 19 is the sum of the product of its digits plus the digits.
Here is another problem from 2001 AMC10:
Suppose that n is the product of three consecutive integers and that n is divisible by 7. Which of the following is not necessarily a divisor of n?
The list of choices is: 6, 14, 21, 28, 42. Your solution might go like this: the product of three consecutive numbers is divisible by 6. Hence, n is divisible by 42. So, the answer must be 28. To check you might consider a product of three consecutive numbers: 5*6*7=210 and see that it is not divisible by 4, hence it is not divisible by 28.
Rule 5. Embrace the partial check. It is very important to check your answers fast. Sometimes you can gain speed if you do not check the problem completely, but check it partially. For example, you can check that your answer is one of the two correct answers. There are many methods for partial checking.
Try an example. Sometimes an example doesn't guarantee that your choice is correct, but it increases your confidence in your answer. Here is another problem from 2001 AMC10:
The sum of two numbers is S. Suppose 3 is added to each number and then each of the resulting numbers is doubled. What is the sum of the final two numbers?
The choices are: 2S + 3, 3S + 2, 3S + 6, 2S + 6, 2S + 12. You can reason that increasing each summand by 3, increases the sum by 6. After that doubling each summand increases the resulting sum twice, so the answer is 2S + 12. To check the answer you can use an example. Usually an example doesn't guarantee the confirmation of your answer, but it might help you eliminate some of the wrong answers. For example, if you choose zero and zero as your initial two numbers, then S = 0, and your transformation brings the result to 12, which confirms your answer 2S + 12. In this particular case, a very easy specific example excluded all the wrong answers.
Divisibility. Sometimes it is faster to calculate the remainder of the answer by some number.
For example, look at the following problem from 2003 AMC10:
What is the units digit of 132003?
The choices are 1, 3, 7, 8, 9. We can immediately say that the answer must be an odd number.
Approximation check. One important example of a partial check is an approximation check. By estimating an approximate answer you might exclude most of the wrong answers. Consider this problem from 2001 AMC12:
How many positive integers not exceeding 2001 are multiples of 3 or 4 but not 5?
The divisibilities by 3, 4 or 5 shouldn't correlate with each other. Approximately one third of those number are multiples of 3 and one quarter are multiples of 4. Let's say that one twelfth are multiples of both 3 and 4. Hence, we estimate the portion of numbers that are multiples of 3 or 4 as 1/3 + 1/4 – 1/12 = 1/2. We have about 1,000 such numbers. The number of numbers that are, in addition, not divisible by 5, are less than that. So out of the given choice of (A) 768, (B) 801, (C) 934, (D) 1067, (E) 1167, we can immediately confirm that the answer is among the first three.
The methods above can be useful even if you do not have multiple choices. But if you do…
Rule 6. Use given choices as extra information. In the previous examples you saw how to use a partial check to exclude some of the choices. Here is a specific example from 2006 AMC10-A of how to exclude choices:
What non-zero real value for x satisfies (7x)14 = (14x)7?
The choices are: 1/7, 2/7, 1, 7, 14. If you solved the problem directly, to check it you can reason why other choices do not work. In this particular case it can be done very fast. 1/7 doesn't work because the left part of the equation becomes 1 when the right is clearly not. 1 and 7 do not work because the left part is odd and the right is even; 14 doesn't work because the left is clearly bigger than the right.
Rule 7. Use meta considerations. If you get into the mind of the designers you can better anticipate when you should check more thoroughly. Consider this problem from 2006 AMC10-A:
A digital watch displays hours and minutes with AM and PM. What is the largest possible sum of the digits in the display?
The most common mistake would be to assume that 12:59 supplies the largest sum, which is 17. But look at the choices: 17, 19, 21, 22, 23. When the designers are asking to find the largest number with some property, they assume that some students will make a mistake and chose a smaller number over a larger one. That means the designers would include this potential mistake among the choices. So the answer is extremely unlikely to be the smallest number on the list of choices. Thus, if you think the answer is 17, understanding how these problems are constructed should alert you to thoroughly check your answer. Indeed, the correct answer is 23 which corresponds to 9:59. Not surprisingly, it is the largest on the list of choices.
AMC 10/12 is coming on February 8 and HMMT on February 12. Happy checking.
I've been celebrating my 29th birthday for many years. Once, when I was actually 45 and wanted to have a big party, I invited everyone to the 5th anniversary of my 29th birthday.
Last week my son turned 29 and I realized that it is time to drop this beautiful, prime, evil, deficient, lazy-caterer number, that in addition is the largest power of two to have all different digits. No more celebrating 29.
For my next age, I picked 42. Not because it is the smallest abundant odious number, but rather because it is the answer to life, the universe and everything.
Thank you everyone who congratulated me on my birthday two days ago. For your information, from now on I am 42.
As I did for 2010 and for previous years, here are math-related puzzles from the MIT Mystery Hunt 2011.
Two more puzzles deserve a special mention for their nerdiness. My teammates loved them.

Tired of the same old sudoku? Here's an opportunity to try many variations of it. Thomas Snyder and Wei-Hwa Huang wrote a book called Mutant Sudoku. The authors are both Sudoku champions. I like the book because the authors are trying to bring everyone up to their level, rather than dumbing down their puzzles. So the book is not at all boring as are most Sudoku books.
The book contains about 180 fun puzzles. Look at the variety:
Wei-Hwa Huang kindly sent me this sample Thermo Sudoku puzzle from the book to use on my blog. The grey areas represent thermometers. Every particular thermometer has to have numbers in increasing order (not necessarily consecutive) starting from the bulb.

The second book by the same authors Sudoku Masterpieces: Elegant Challenges for Sudoku Lovers, is itself a masterpiece. With about 100 puzzles, there are fewer than in the first book, but there are more types of puzzles. As a consequence, you'll have less practice for each particular type, but more variety. In addition, as you can see from the cover, the second book is elegantly designed.
I bought both books and immediately started scribbling in the first one. My bad handwriting would seem so out of place in the beautiful second book that I have not even started working in it yet. Maybe I will give it as a gift to someone with better penmanship.
Two days ago I threw at my readers the following problem:
A plane takes off and goes east at a rate of 350 mph. At the same time, a second plane takes off from the same place and goes west at a rate of 400 mph. When will they be 2000 miles apart?
The purpose of throwing this problem was to discuss the nature of the implicit assumptions that we are asked to make when solving math problems, and the implicit assumptions we teach our children to make when we teach them to solve math problems. This is especially important for problems like this, that are phrased in terms of a situation in the real world. The real world is too complex to model all of; the great power of mathematics is that sufficiently idealized situations are predictable. But which idealizations are appropriate? How does one choose? How does one teach youngsters what to choose?
Before I get to the actual discussion, however, I want to re-throw this problem at my readers, in an effort to highlight what originally jumped out at me as being wrong with it.
Neglecting the effects of altitude, differential wind, acceleration, relativity, measurement error, finite size and non-superimposability of the planes, and the Earth's deviations from perfect sphericity,
- Find how much time it takes them to become 2000 miles apart, assuming that the planes are starting from Boston and the distance is measured as
- a straight line in 3-space.
- the shortest surface distance.
- How far from the closest pole may the starting point be located, so that the answer to the problem is "never"? Solve separately for
- the 3D distance.
- the shortest surface distance.
- What portion of the Earth's surface do the "never"-locations of the previous question occupy?
- under the 3D distance?
- under the shortest surface distance?
Hint: The easiest question is 2b.
My Jewish ex-father-in-law, Naum Bernstein, is 96 years old and is full of life. He has a joke for every situation. In the last decade he wrote several volumes of memoirs in Russian. One of the books was a collection of his favorite jokes and his explanations of them. I decided to retell some of the jokes from his selection.
An arithmetic teacher calls the student Rabinovich to the blackboard. "It is known that from 1 kilogram of sour cream you can make 200 grams of butter. Imagine, Rabinovich, that your father bought 2 kilograms of sour cream. How much butter can he make?"
"Five hundred grams," Rabinovich replies.
The teacher frowns, "Rabinovich, you do not know arithmetic!"
Rabinovich answers, "Sir, you do not know my father."
An astronomy teacher explains that in the future the Earth will lose its heat energy, continents will collide, and solar radiation will increase. In six billion years life will be extinct. A student looking really scared raises his hand and asks, "In how many years will life become extinct?"
"In about six billion years," the teacher repeats.
"Whew," says the student, "you got me so scared. I thought you said six million."
Two professors are chatting while watching a soccer game. The first one says, "They say that soccer players have their brains in their legs. So their heads are really empty."
"Not quite," the second professor replies. "The player on the right passed my exam yesterday."
The first professor expresses interest, so the second one elaborates. "As a rule, I ask two questions. If the student gives a correct answer to one of them, he passes."
"So, what did you ask that guy?"
"My first question was 'What color are red blood cells?' He answered 'Yellow.' That was an incorrect answer. The second question was 'How is sulfuric acid produced?' To this he replied, 'I do not know,' which was absolutely true, so he passed."
A Russian literature teacher asks a pupil, "Who wrote Eugene Onegin?" The pupil gets scared that he is being blamed for something and replies, "No, not me! I swear I didn't write it!" Everyone laughs. The teacher decides that the pupil disrupted the class on purpose and asks for his father to come by.
The father arrives and after the teacher explains what happened, the father says, "Maybe he is not guilty; maybe he really didn't write it. I doubt that he is capable of writing anything."
The teacher is stunned and later tells the whole story in the teachers' lounge to her colleagues. An astronomy teacher comes home and retells the story to her husband who works for the KGB. The husband comments, "Do not worry, we are on it. Three people already confessed to writing it."
A hardcore anti-Semite was dying. As he got weaker he made a last request. He wanted to convert to Judaism. Everyone was extremely surprised, but decided not to interfere. After the conversion, his wife summoned the courage to ask him what was going on. "Do you think you were mistaken, hating Jews all your life?"
"No," he replied happily, "But now with my death, the world will get rid of one more Jew."
An old Jew comes to a Rabbi and asks if he can shave his beard off, because his children think that he is old-fashioned. The Rabbi tells him that by Jewish law he is not allowed to shave. The old man turns to go home when he realizes that the Rabbi himself doesn't have a beard. He stops and asks, "Dear Rabbi, you just forbade me to shave my beard, but how come you are clean-shaven yourself?"
The Rabbi replies, "I didn't ask anyone's permission."
When Rabinovich came to a bureaucrat with a request, the bureaucrat replied, "Come back tomorrow." Rabinovich returned the next day and received the same reply. Rabinovich was very persistent and returned day after day.
Finally, the bureaucrat lost his patience and attacked Rabinovich, "This is outrageous! Don't you understand simple language? I keep telling you to come tomorrow and you keep coming today."
The communist committee of a supermarket in the USSR received a lot of complaints about the rudeness of their salespeople. The committee decided to improve the quality of service and provided special training in which salespeople were taught politeness. The training emphasized what to do in case a particular item was unavailable. The salespeople were supposed to politely explain that the item is temporarily unavailable and to offer a substitute.
The next thing one of their salespeople said to a customer was "I am very sorry, we are temporarily out of toilet paper. May I offer some sandpaper?"
There is panic in an apartment on the 13th floor. The wife recognizes the sound of her husband's approach, even though he was supposed to be on a business trip. The lover asks, "What should I do, honey?"
"What do people do in such cases? Jump out the window!"
"But we are on the 13th floor!"
"This is no time for superstition!"
A young man had smelly feet, plus he always forgot to change his socks. His girlfriend got tired of it and asked him to promise that he would always change his socks before coming to see her.
Next visit the young man smelled as bad as ever. Outraged, the girl said, "But you promised to change your socks!"
The young man answered, "I did as I promised."
"I don't believe you, you smell awful."
"I was sure you wouldn't believe me. Good thing I brought my dirty socks with me as proof."
At the 50th anniversary of a very happy couple, someone asked the husband for their secret. He said that right before the wedding they agreed that the husband would decide all the crucial and very important things, and the wife would be responsible for all minor decisions. "For example," he continued, "yesterday I decided that the US should withdraw their troops from Iraq, and my wife decided where to buy our vacation house."
Two long-time girlfriends meet after several years without being in touch. "How are your children?" asks one of them.
The other replies, "My daughter is fine, she married a nice young man, who is providing for her. He also helps her with chores and even brings her coffee in bed every morning."
"What about your son?"
"It's a disaster. I don't know what to do. He married a really lazy woman. Even though she's not working, she wants him to help her with the chores. Can you imagine that? She even dared to ask him to bring her coffee in bed every morning."
Two friends are walking along a street very late at night. Robbers attack them with guns, demanding their wallets. One of the friends asks the robbers, "Can you give me 30 seconds?" The robbers agree. He takes out $100 from his wallet and gives it to his friend, "Remember I owed you $100? I am paying back my debt in front of witnesses."
Life is a struggle. Before lunch with hunger, after lunch with sleepiness.
A mother says to her son, "Please, close the window — it's cold outside."
The son replies, "Do you think it will get warmer outside if I close the window?"
How are pessimists and optimists different from normal people?
A pessimist uses both a belt and suspenders, an optimist uses neither.
In a cemetery there is a beautiful monument with a picture of a bald, wrinkled old man. He is smiling, showing his perfect white teeth. His epitaph says:
Here lies Mr. X, who lived more than 100 years, lost his hair, became all wrinkled, but kept his perfect teeth. That is because he always used our company's toothpaste.
A nearby monument has a picture of an old toothless woman with beautiful, voluminous hair. The inscription explains which brand of shampoo she used.
Many other tombstones with ads are scattered throughout the cemetery. But in the middle there is a huge mausoleum with an inscription reading:
No one is buried here and no one ever will be, because his or her parents used condoms made by our company.
A Russian man marries an American woman. After a while he writes a letter home.
My wife must be very dirty. She showers every day.
Rabinovich was asked why he didn't attend the last committee meeting. He replied, "If I knew it was the last, I would certainly have come."
I stumbled upon the following problem in Mathematics Teacher v.73 (September 1980):
A plane takes off and goes east at a rate of 350 mph. At the same time, a second plane takes off from the same place and goes west at a rate of 400 mph. When will they be 2000 miles apart?
Ooh, boy!
Question for my readers: explain my reaction.
I have a leased Toyota Corolla, and I am happily enrolled in AutoCheck payments with Toyota's Financial Services. So I do not even look at my bills. Once I opened my bill and noticed that the requested payment was twice as high as I expected. I looked closer and the bill had a car tax included in it. I looked even closer and read that:
Your Current Payment Due will be automatically withdrawn from your checking or savings account on the above Payment Due Date or the next banking day.
I decided that everything was taken care of and continued my relaxed life. After several months I checked my bill again, and the car tax was still there. After more careful study of my bill I discovered that Toyota's "Current Payment Due" doesn't include my car tax. Obviously they assume that their definition of "Current Payment Due" is crystal clear to everyone.
I got worried about this delayed car tax payment and went online to pay it. I tried to make this payment, but Toyota's website rejected it. The website informed me that because I am enrolled in AutoCheck, I am not allowed to make separate online payments. I couldn't believe it: to do so, I would have to de-enroll first!
So I just wrote a check.
In one day my feelings for my Toyota Corolla were turned around. If their financial system is designed so stupidly, what can we say about their car designs? Suddenly the sound of my brakes and the squeak in my steering wheel worry me.
A year ago I posted a chessboard puzzle. Recently I stumbled on a September 2008 issue of "Math Horizons" where it was presented as a magic trick.
When the magician leaves the room, the trickees lay out eight coins in a row deciding which side is turned up according to their whim. They also think of a number between 1 and 8 inclusive. The magician's assistant then flips exactly one of the coins, before inviting the magician back in. The magician looks at the coins and guesses the number that the trickees thought of.
The magician's strategy can be derived from the solution to the chessboard puzzle. The assistant numbers the coins from zero to seven from left to right. Then s/he flips the coin so that the parity addition (XORing) of all the numbers corresponding to heads is the number that the magician needs to guess. For this trick to work, the number of coins needs to be a power of 2.
Andrey Zelevinsky posted (in Russian) a cool variation of this trick with two decks of cards.
The magician has two identical card decks and he is out of the room for now. A random person from the audience thinks of a card. Next, the audience chooses several cards from the first deck. Then the assistant adds one card from the second deck to the set of chosen cards, lays them on a table, and then invites the magician back. The magician looks at the cards on the table and guesses the card that was thought of.
Unlike in the coin trick above, the number of cards in the deck doesn't need to be a power of 2. This flexibility is due to the fact that the magician has two decks of cards, as opposed to one set of coins. Having the second deck is equivalent to the assistant in the coin trick being allowed to flip one or ZERO coins.
Nikolay Konstantinov, the creator and the organizer of the Tournament of the Towns, discussed some of his favorite tournament problems in a recent Russian interview. He mentioned two beautiful geometry problems by Sergey Markelov that I particularly loved. The first one is from the 2003 tournament.
An ant is sitting on the corner of a brick. A brick means a solid rectangular parallelepiped. The ant has a math degree and knows the shortest way to crawl to any point on the surface of the brick. Is it true that the farthest point from the ant is the opposite corner?
The other one is from 1995.
There are six pine trees on the shore of a circular lake. A treasure is submerged on the bottom of the lake. The directions to the treasure say that you need to divide the pine trees into two groups of three. Each group forms a triangle, and the treasure is at the midpoint between the two triangles' orthocenters. Unfortunately, the directions do not explain how exactly to divide the trees into the groups. How many times do you need to dive in order to guarantee finding the treasure?
Perfidy is to parity as odious is to odd and evil is to even. As a reminder, odious numbers are numbers with an odd number of ones in their binary expansions. From here you can extrapolate what the evil numbers are and the fact that the perfidy of an integer is the parity of the number of ones in its binary expansion. We live in a terrible world: all numbers are perfidious.
So why are we writing about the perfidy of negative numbers? One would expect it to be a natural extension of the perfidy of positive numbers, but it turns out that the naive way of defining it doesn't work at all. Is there hope? Could negative numbers be innocent of evil and free of odiousness? Is zero an impenetrable bulwark against perfidy? Not quite, but something interesting does happen to evil as it tries to cross zero. Read on.
To define perfidy for negative numbers, let us study how perfidy behaves for positive numbers. It is easiest to think about the perfidies of power-of-two-sized chunks of non-negative integers at a time. Let us denote by Tn the string of perfidies of the integers from 0 to 2n−1, with evil being zero and odious being 1. So T0 = 0, T1 = 01, T2 = 0110, T3 = 01101001, …. The recurrence relation governing the Tn is Tn+1 = TnTn, where T is the bitwise negation of the string T, and juxtaposition is concatenation. The limit of this as n tends to infinity is the (infinite) sequence of perfidies of non-negative integers. This sequence is called the Thue-Morse sequence: 0,1,1,0,1,0,0,1,1,0,0,1,0,1,1,0,1,0,0,….
So defining the perfidy of negative numbers is equivalent to extending the Thue-Morse sequence to the left. If we are to define "the" perfidy of negative numbers, that definition should preserve most of the properties of the Thue-Morse sequence after extension.
So, let's see. We asked around, and most people said that the binary expansion of a negative integer should be the binary expansion of its absolute value, but with a minus sign. Defining perfidy as parity of number of ones in this binary expansion corresponds to the following extended Thue-Morse sequence in which we mark values corresponding to negative indices with bold font: … 0, 1, 1, 0, 1, 1, 0, ….
One of the major properties of the Thue-Morse sequence is its fractal property: if you replace every zero of the Thue-Morse sequence by 0,1 and every one by 1,0, you will get the Thue-Morse sequence back. Clearly, our new extended sequence doesn't have this property.
Another set of properties for the Thue-Morse sequence, called avoidance properties, is a long list of patterns that the sequence avoids. For example, the Thue-Morse sequence doesn't contain any overlapping squares — patterns axaxa, where a is a character and x is a word. But you can see above, our first extension contains it. So this definition is wrong, not just once but twice (and two wrongs only make a right under very unusual circumstances). Perfidy is stymied by the cross-over from zero to minus one. Are negative numbers protected from the ravages of evil? (and odiousness?)
Unfortunately, there are many people, for example John Conway, who inadvertently extend the reach of perfidy by arguing that the binary expansion of a negative integer should be different. Indulge in a flight of fancy and imagine the binary expansion that consists of infinitely many ones to the left: …1111. What happens when you add 1 to it? The carry gets pushed infinitely far away, and you get …000000 — zero. So it is quite reasonable to let …1111 be the binary expansion of −1. Similarly, the string …1110 represents −2, …1101 represents −3, etc. Continuing this we see that the binary expansion of a negative integer −n is the bitwise negation of the binary expansion of n − 1 (including the leading zeros). This is called the Two's complement representation.
Why is two's complement a reasonable representation? Suppose you were trying to invent a binary notation for negative numbers, but you wanted to pursue uniformity by not using a minus sign. The problem is that the standard definition of the binary representation allows you to represent only positive numbers. But you can solve this problem with modular arithmetic: modulo any fixed N, every negative number is equivalent to some positive number (by adding enough multiples of N), so you can just represent it by representing that positive number. If you choose N to be a power of two, modding out by it is just truncation of the binary representation. If you let those powers of two tend to infinity, you get the two's complement representation described above.
Aside: When you are building a computer, uniformity is money, because special cases cost special transistors. The two's complement idea lets one build arithmetic units that just operate on positive numbers with some number of bits (effectively doing arithmetic modulo 2k), and leave the question of negativeness to the choice of representatives of those equivalence classes.
If we take two's complement as the binary expansion of negative numbers, how will we define the perfidy? Is the number of ones in the infinite string …1111 corresponding to −1 even or odd?
We can't answer that question, but we know for every binary expansion of negative numbers the parity of the number of zeroes. Thus we can divide all negative integers in two classes with different perfidy. We just do not know which one is which.
Let us consider two cases. In the first case we consider a negative number odious if the number of zeroes in its binary expansion is odd. The corresponding extended Thue-Morse sequence is: … 0, 1, 1, 0, 0, 1, 1, 0, …. The negative half is the reflection of the classical Thue-Morse sequence. In the second case we consider a negative number odious if the number of zeroes in its binary expansion is even. The corresponding extended Thue-Morse sequence is: … 1, 0, 0, 1, 0, 1, 1, 0, …. The negative half is the bitwise negation of the reflection of the classical Thue-Morse sequence.
Can we say that one of the sequences is better than the other? Both of them respect the fractal property of the classical Thue-Morse sequence. Let us look at the avoidance properties. The avoidance properties are symmetric with respect to switching zeroes with ones and with respect to changing the direction of the sequence. Hence, the negation, the reflection, and the reflection of the negation of the Thue-Morse sequence will continue to respect these properties.
Thus, we only need to check the avoidance properties of the finite subsequences that span both negative and non-negative indices. We claim that for both definitions of perfidy, any finite middle subsequence of the extended Thue-Morse sequence occurs as a subsequence in the classical Thue-Morse sequence. So any avoidance properties that are true for the Thue-Morse sequence will also be true for both extensions.
Indeed, it is easy to show that the strings T2n defined above are palindromes. So for the first definition of perfidy the string in the middle will be a substring of T2nT2n for some large n, and for the second definition a substring of T2nT2n. But the classical Thue-Morse sequence contains the subsequence T2nT2nT2nT2nT2nT2nT2nT2n. So whichever way we extend the Thue-Morse sequence to the left any finite middle part will always be a repetition of a piece in the classical Thue-Morse sequence. Thus, all the avoidance properties will hold.
We see that there are two logical ways to define perfidy for negative integers. There are two clear groups of numbers with the same perfidy, but which is called evil and which odious is interchangeable. So evil doesn't stop at zero after all, but at least it gets an identity crisis.
Last revised October 2013