
This blog has a modern version at http://blog.tanyakhovanova.com/, where you can leave comments. This page contains the copies of 86 blog entries for 2016, 2017, and 2018. The latest essays are at http://www.tanyakhovanova.com/MathBlog.html

Alex Bellos sent me his new book Puzzle Ninja: Pit Your Wits Against The Japanese Puzzle Masters. What has he done to me? I opened the book and couldn't close it until I solved all the puzzles.
This is a fantastic book. There are many varieties of puzzles, including some types that I've never seen before. Also, the beautifully designed puzzles are great. Often puzzles of the same type target different solving ideas or have varied cool themes.
This book is more than a bunch of puzzles; it also contains poetic stories about puzzle histories and Japanese puzzle designers. Fantastic puzzles together with a human touch: this might be my favorite puzzle book.

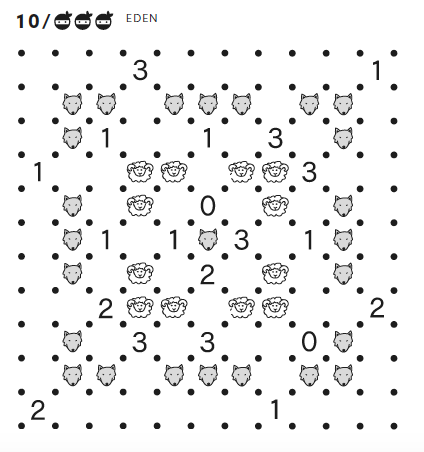
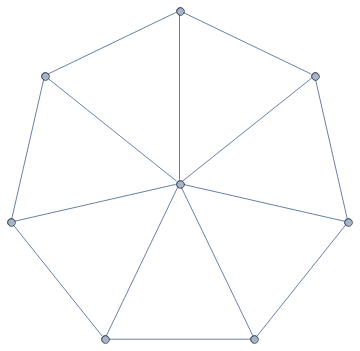
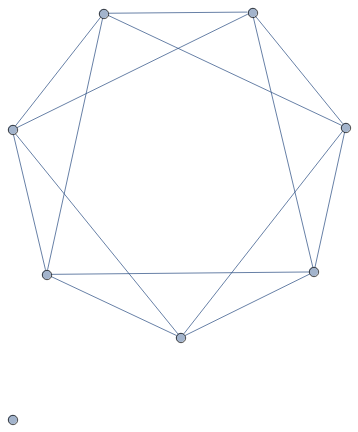
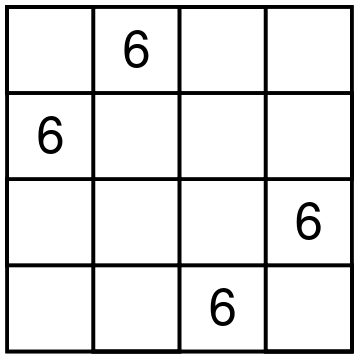
I present two puzzles from the book. The puzzle type is called Wolf and Sheep Slitherlink. The Slitherlink is a famous puzzle type with the goal of connecting some of the neighboring dots into a single non-self-intersecting loop. A number inside a small square cell indicates how many sides of the square are part of the loop. Wolf and Sheep Slitherlink is a variation of Slitherlink in which all sheep should be kept inside the fence (loop) and all the wolves outside.
Ignore the numbers in the title as they just indicate the order number of Wolf and Sheep Slitherlink puzzles in the book. The number of ninja heads shows the level of difficulty. (The hardest puzzles in the book have four heads.) The difficulty is followed by the name of the puzzle master who designed the puzzle.
The first puzzle above is slightly easier than the second. I like the themes of these two puzzles. In the first one, only one cell—lonely wolf—marks the relationship to the fence. In the second one, the wolf in the center—who needs to be outside the fence—is surrounded by a circle of sheep who are in turn surrounded by a circle of wolves.
My friend Alex Ryba uses interesting math questions in the CUNY Math Challenge. For the 2016 challenge they had the following problem.
Problem. Eve owns two six-sided dice. They are not necessarily fair dice and not necessarily weighted in the same manner. Eve promises to give Alice and Bob each a fabulous prize if they each roll the same sum with her dice. Eve wishes to design her two dice to minimize the likelihood that she has to buy two fabulous prizes. Can she weight them so that the probability for Alice and Bob to get prizes is less than 1/10?
The best outcome for Eve would be if she can weight the dice so that the sum is uniform. In this case the probability that Alice and Bob get the prizes is 1/11. Unfortunately for Eve, such a distribution of weight for the dice is impossible. There are many ways to prove it.
I found a beautiful argument by Hagen von Eitzen on the stack exchange: Let ai (correspondingly bi) be the probabilities that die A (correspondingly B) shows i + 1. It would be very useful later that that i ranges over {0,1,2,3,4,5} for both dice. Let f(z) = ∑ aizi and g(z) = ∑ bizi. Then the desired result is that f(z)g(z) = ∑j=010 zj/11. The roots of the right side are the non-real roots of unity. Therefore both f and g have no real roots. So, they must both have even degree. This implies a5=b5=0 and the coefficient of z10 in their product is also 0, contradiction.
Alex himself has a straightforward argument. The probabilities of 2 and 12 have to be equal to 1/11, therefore, a0b0 = a5b5 = 1/11. Then the probability of a total 7 is at least a0b5 + a0b5. The geometric mean of a0b5 and a0b5 is 1/11 (from above), so their arithmetic mean is at least 1/11 and their sum is at least 2/11. Therefore, the uniform distribution for sums is impossible.
So 1/11 is impossible, but how close to it can you get?

I just got this picture from my friend Victor Gutenmacher, which I never saw before. My 1975 IMO team is posing at our training grounds before the Olympiad trip to Bulgaria.
Left to right: Boris Yusin, Yuri Ionin, Zoya Moiseyeva (front), Gregory Galperin (back), me, Ilya Yunus, Valentin Skvortsov, Aleksandr Kornyushkin, Sergei Finashin, Sergei Fomin (front), Alexander Reznikov (back), Yuri Shmelev (front), Yuri Neretin (back), Victor Gutenmacher.
Our coaches are in the shot as well. Surprisingly, or not surprisingly, all of them moved to the USA. Yuri Ionin, now retired, was a professor at Central Michigan University. Gregory Galperin is a professor at Eastern Illinois University. Sergei Fomin is a professor at the University of Michigan. Victor Gutenmacher worked for BBN Technologies and Siemens PLM Software, and is now retired.
There are two more adults in the picture: Valentin Anatolievich Skvortsov, our leader and Zoya Ivanovna Moiseyeva, our deputy leader. Skvortsov was working at the math department of Moscow State University at that time. The University was angry that he didn't block some students with Jewish heritage from the team thus allowing them to be accepted to Moscow State University without exams. I wrote a story of how Zoya persuaded Alexander Reznikov not to go to Moscow University to help Valentin. It ruined Alexander's live, and didn't even help Valentin. 1975 was Valentin's last trip as the leader.
An orchestra of 120 players takes 70 minutes to play Beethoven's 9th Symphony. How long would it take for 60 players to play the symphony?

I do not like making objects with my hands. But I lived in Soviet Russia. So I knew how to crochet, knit, and sew — because in Russia at that time, we didn't have a choice. I was always bad at it. The only thing I was good at was darning socks: I had to do it too often. By the way, I failed to find a video on how to darn socks the same way my mom taught me.
Then I came to the US. I suddenly found myself in a rich society, where it was cheaper to buy new stuff than to spend the time doing things with my hands. So I happily dropped my craftsmanship.
After not working with my hands for 28 years, one day I needed hyperbolic surfaces for my classes and I couldn't find any to buy. Hyperbolic surfaces are famous for providing an example when the Euclid's Fifth axiom doesn't work. These hyperbolic surfaces look flat locally, so you can continue a line in any given direction. If you draw a line on such a surface and pick a point that is not on the line, then you can draw many lines through the point that are parallel to the given line.
My students are more important than my dislike of crochet, so I decided to just do it myself. I asked my friend Debbie, who knows how to crochet, for advice, and she gave me more than advice. She gave me a hook and a piece of yarn and reminded me how to work the hook. She started me with a small circle. After that all I had to do was add two stitches for each stitch on the perimeter of the circle. The finished product is this green ballish thing that looks like a brain, as in the photo.
Outside the starting circle, each small surface segment of this "brain" looks the same, making the "brain" a surface of constant curvature.
I chose a ratio of 2 to 1, adding two new stitches for each previous stitch. With this ratio, my flattish surface started looking like a ball very fast. The length of the perimeter doubled for every row. Thus each new row I crocheted took the same total amount of time that I had already spent on the whole thing. All the hours I worked on this "brain," I kept thinking: darn, it is so unrewarding to do this. Annoying as it was, the thing that kept me going was my initial decision to continue to use up all the yarn Debbie had given me. In the end, with this ratio, half the time I worked was spent making the final row.
We can inflate one permutation with another permutation. Let me define the inflation by examples and pictures. Suppose we have a permutation 132 which we want to inflate using permutation 21. The result is the permutation 216543 that can be divided into three blocks 21|65|43. The blocks are ordered as the first permutation 132, and within each block the order is according to the second permutation. This operation is often called a tensor product of two permutations. The operation is non-commutative: the inflation of 21 with 132 is 465132.
As one might guess this post is related to k-symmetric permutations, that is, permutations that contain all possible patterns of size k with the same frequency. As I mentioned in my recent post 3-Symmetric Permutations, the smallest non-trivial examples of 3-symmetric permutations are 349852167 and 761258943 in size 9.
A permutation is called k-inflatable if its inflation with k-symmetric permutation is k-symmetric. One of my PRIMES projects was about 3-inflatable permutations. The result of this project is the paper On 3-Inflatable Permutations written with Eric Zhang and posted at the arxiv.
The smallest non-trivial examples of 3-inflatable permutations are in size 17: E534BGA9HC2D1687F and B3CE1H76F5A49D2G8, where capital letters denote numbers greater than nine. Another cool property discovered in the paper is that the tensor product of two k-inflatable permutations is k-inflatable.
I am fascinated by 3-symmetric permutations, that is, permutations that contain all possible patterns of of size three with the same frequency. As I mentioned in my recent post 3-Symmetric Permutations, the smallest non-trivial examples are in size 9.
When I presented these examples at a combinatorics pre-seminar, Sasha Postnikov suggested to draw the permutations as a graph or a matrix. Why didn't I think of that?
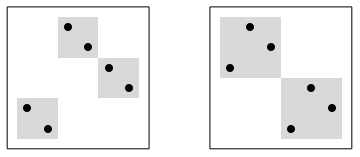
Below are the drawings of the only two 3-symmetric permutations of size 9: 349852167 and 761258943.
As I already mentioned in the aforementioned essay the set of 3-symmetric permutations is invariant under the reversal and subtraction of each number from the size of the permutation plus 1. In geometrical terms it means reflection along the vertical midline and central symmetry. But as you can see the pictures are invariant under 90 degree rotation. Why?
What I forgot to mention was that the set of k-symmetric permutations doesn't change after the inversion. In geometrical terms it means the reflection with respect to the main diagonal. If you combine a reflection with respect to a diagonal with a reflection with respect to a vertical line you get a 90 degree rotation. Overall, the symmetries of the k-symmetric permutations are the same as all the symmetries of a square. Which means we can only look at the shapes of the k-symmetric permutations.
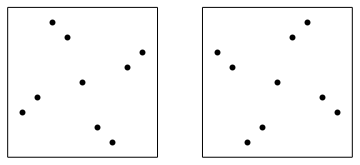
There are six 2-symmetric permutations: 1432, 2341, 2413, 3142, 3214, 4123. As we can see in the picture below they have two different shapes.

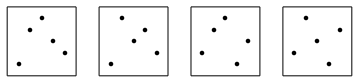
Here is the list of all 22 2-symmetric permutations of size 5: 14532, 15342, 15423, 23541, 24351, 24513, 25143, 25314, 31542, 32451, 32514, 34152, 34215, 35124, 41352, 41523, 42153, 42315, 43125, 51243, 51324, 52134. The list was posted by Drake Thomas in the comments to my essay. Up to symmetries the permutations form four groups. Group 1: 14532, 15423, 23541, 32451, 34215, 43125, 51243, 52134. Group 2: 15342, 24351, 42315, 51324. Group 3: 24513, 25143, 31542, 32514, 34152, 35124, 41523, 42153. Group 4: 25314, 41352. The picture shows the first permutation in each group.
In my previous post I described 3-symmetric permutations. Now I want to define 3-symmetric graphs.
A reminder: a k-symmetric permutation is such that the densities of all permutations of size k in it are the same. In particular a 2-symmetric permutation has the same number of inversions and non-inversions. How do we translate this to graphs? I call a graph 2-symmetric if it has the same number of edges as non-edges. 2-symmetric graphs are easy to construct, but they only exist if the number of vertices, n, is such that n choose 2 is even. The simplest non-trivial examples are graphs with 4 vertices and three edges.
The above definition is difficult to generalize. So I rephrase: a graph G is 2-symmetric, if the density of any subgraph H with 2 vertices in G is the same as the expected density of H in a random graph where the probability of an edge equals 1/2. This definition is easy to generalize. A graph G is k-symmetric, if the density of any subgraph H with k vertices in G is the same as the expected density of H in a random graph where the probability of an edge equals 1/2. In particular, here are the densities of all four possible subgraphs with 3 vertices in a 3-symmetric graph:
For a graph G to be 3-symmetric, the number of vertices, n, in G needs to be such that n choose 3 is divisible by 8. The first non-trivial case is n = 8. Here are the pictures of two 3-symmetric graphs. The first one is a wheel, and the second one is its complement.
I want to study patterns inside permutations. Consider a permutation of size 4: 1432. Today I am excited by ordered subset of size 3 inside this permutation. For example, I can drop the last number and look at 143. The ordering in 143 is the same as in 132, or, as a mathematician would say, 143 is order-isomorphic to 132. In my example of 1432, I have four subsets depending on which number I remove: 432 is order-isomorphic to 321, while 132, 142 and 143 are all order-isomorphic to 132.
The density of a pattern 123 in the permutation 1432 is the ratio of subsets of size 3 that are order-isomorphic to 123 to all subsets of size 3. As I already calculated, the density of 123 in 1432 is zero, while the density of 321 is 1/4, and the density of 132 is 3/4.
A permutation is called 3-symmetric if the densities of all patterns of size 3 (123, 132, 213, 231, 312, 321) are the same. The reason I love this notion, is that 3-symmetric permutations are similar to random permutations with respect to patterns of size 3.
My example permutation, 1432, is not 3-symmetric. Thinking about it, no permutation of size 4 can be 3-symmetric. The number of subsets of size 3 is four, which is not divisible by 6.
I wanted to find 3-symmetric permutations. So the size n of the permutation needs to be such that n choose 3 is divisible by 6. The numbers with this property are easy to find. The sequence starts as 1, 2, 9, 10, 18, 20, 28, 29, 36, 37, 38, 45, 46. The sequence is periodic with period 36.
Any permutation of sizes 1 or 2 is 3-symmetric as all densities are zero. Duh!
The next interesting size is 9. My student, Eric Zhang, wrote a program and found that there are two 3-symmetric permutations of size 9: 349852167 and 761258943. These numbers are so cool!. First, they are reverses of each other. This is not very surprising: if a permutations is 3-symmetric, then its reverse must also be 3-symmetric. There is another property: the permutations are rotational symmetries of each other. That is, the sum of two digits in the same place is 10. You can see that rotating a 3-symmetric permutation produces a 3-symmetric permutation.
I decided to write a program to find 3-symmetric permutations of the next size: 10. There is none. I do not trust my programming skills completely, so adjusted my program to size 9 and got the same result as Eric. I trust Eric's programming skills, so I am pretty sure that there are no 3-symmetric permutations of size 10. Maybe there are some 3-symmetric permutations in size 18.
Let's find 2-symmetric permutations. These are permutations with the same number of ascends and descends inversions and non-inversions. For n to be the size of such permutation n choose 2 needs to be divisible by 2. That means n has to have remainder 0 or 1 modulo 4. The first nontrivial case is n = 4. There are six 2-symmetric permutations: 1432, 2341, 2413, 3142, 3214, 4123. We can also group them into reversible pairs: 1432 and 2341, 2413 and 3142, 3214 and 4123. If we look at rotational symmetry we get different pairs: 1432 and 4123, 2341 and 3214, 2413 and 3142.
You can try to find non-trivial 4-symmetric permutations. Good luck! The smallest nontrivial size is 33. Finding 5-symmetric permutations is way easier: the smallest nontrivial size is 28. The sequence of nontrivial sizes as a function of n is: 1, 4, 9, 33, 28, 165, 54, 1029, 40832, 31752, 28680, 2588680, 2162700, and so on. My computer crashed while calculating it.
I found this puzzle on the Russian QWERTY channel.
Five people sit around a table playing Mafia. Among them are two innocent people, two Mafiosos, and one detective. The Mafia people know each other; the detective knows who each of them is; and the innocent people have no information whatsoever about anyone at the table.
During this particular game, the innocents and the detective always tell the truth, while mafia people always lie. They start by going around the circle making the following statements:
- A: I know who B is.
- B: I know who the detective is.
- C: I know who B is.
- D: I know who E is.
Who is who?
Once John Conway showed me a cute way to enumerate Latin squares of size 4, up to the movements of the plane. It was a joint result with Alex Ryba, which is now written in a paper Kenning KenKen.
For starters, I want to remind you that a Latin square of size n is an n by n table filled with integers 1 through n, so that every row and column doesn't have repeated integers. KenKen is a game that John Conway likes, where you need to recover a Latin square given some information about it.
Let me start by describing a particular shape of four cells that one digit can occupy in a Latin square of size 4. There are only seven different shapes. To get to the beautiful result, we need to number these seven shapes in a particular order starting from zero. The shapes are shown below.
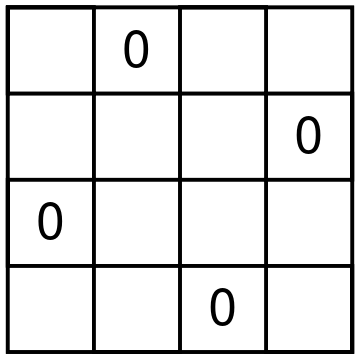
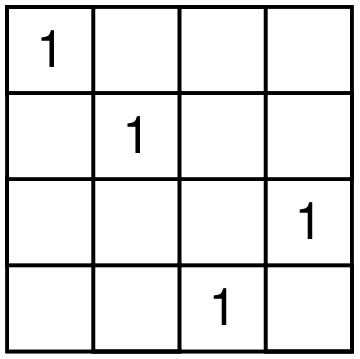
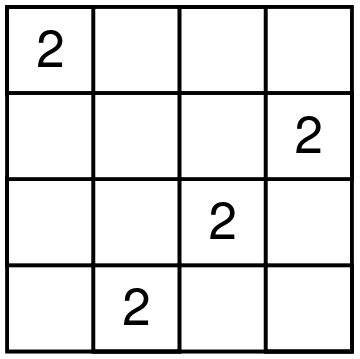
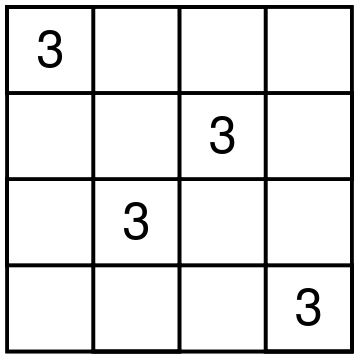
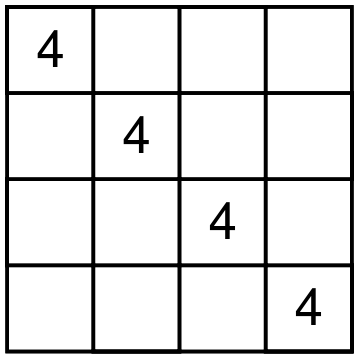
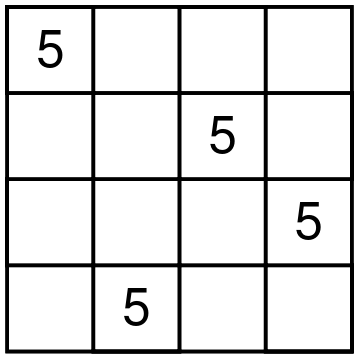
There are 12 different Latin squares up to movements of the square and relabeling the digits. Here is how Conway and Ryba matches shapes and squares. For each Latin square, take the shapes of all four digits, remove the duplicate shape numbers and sum the leftover shape numbers. You will get a unique number from 1 to 12 that represents a particular Latin square. For example, consider the square on the picture below.
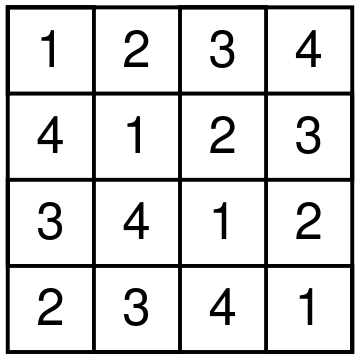
Digit 1 is shape 4, digits 2 and 4 form shape 2, and digit 3 forms shape 6. Shape 2 is used twice, and we ignore multiplicities. So we have shapes 2, 4, and 6 used. The resulting Latin square is number 2 + 4 + 6, that is 12. It is a fun exercise to try to find all the squares. For example, square 1 can only use shapes 0 and 1. But shape 1 uses exactly one corner. So the first square should use each of the digits in shape 1.
John likes finding interesting ways to remember which shape is which. You can find his and Alex's suggestions in the paper which Alex submitted to the arxiv.
Oops! While I was writing this essay, arxiv rejected the paper.
My coauthor, Konstantin Knop, sent me a coin-weighing problem that is really good. Surprisingly, it is old: it first appeared in a Russian math journal, Kvant, in 1973.
Puzzle. At a trial, 14 coins were presented as material evidence. The expert tested the coins and discovered that seven of them were fake, the rest were real, and he knew exactly which coins were fake and which were real. The court only knows that counterfeit coins weigh the same, real coins weigh the same, and fake ones are lighter than real ones. The expert wants to use not more than three weighings on a balance scales without weights to prove to the court that all the counterfeit coins he found are really fake, and the rest are real. Could he do it?
A cartoon based on my script is posted on TEDEd: Can you solve the Leonardo da Vinci riddle?.
There is only one correct answer to this puzzle. Choices:

My mom died in April of 2017. I didn't even consider flying to Russia for her funeral. April-May is my most demanding work period. We were preparing for the annual PRIMES conference. Four of the projects that I personally mentor were presented at the conference. As a head mentor, I was also helping on all the other projects. During these months, I do not have time to breath.
I felt intensely guilty missing the funeral, but I blocked my emotions and worked. I didn't shed a tear. Come June-July, I have another busy work period running Mathroots and RSI. August is often a slow month, which I usually use to finish papers that I am writing with my students. But in August, 2017, I needed to put the papers aside and give myself time to grieve. My mood was getting darker and darker. At some point I realized that I was depressed. Surprisingly, I still didn't shed a tear.
I had been depressed before, and I do not ever want to be in that place again. I ordered myself to stop mourning, and with some positive self-talk, I was able to get myself out of the depression. In the process I didn't work much in August, leaving me with a huge backlog of papers: I had about 20 papers that needed my immediate attention.
When the academic year began in September, my work was more stressful than ever. On one hand I had a pile of unfinished papers, and on the other hand our programs were growing bigger and more taxing. I limped along and did my best until April of this year. Because I had more stress than ever before. Because April-May is my most intense work time, I had to cancel my social life, stop watching TV, and drop my exercise regime to be able to prepare for our annual PRIMES conference. I was so busy I completely missed the first anniversary of my mom's death. In the year since her death I had been mourning, but I was still unable to cry. When I realized that I had forgotten this date, I felt more severe guilt than ever. I called my sister in Moscow. She told me that she had ignored the death anniversary too. She had done it on purpose. It is better to celebrate life than death, she told me, and it made me feel better.
When the PRIMES conference was over, it was clear that my work was overtaking my life. I decided to go away for a day to rethink my priorities.
I googled Googled around for a place to go, and found the Innisfree garden. The website claimed that the garden is recognized as one of the world's ten best gardens. Sounded fitting for rethinking a life.
The Innisfree Garden is different from other gardens that I have seen. With my untrained eye, I couldn't distinguish what was man-made and what was nature. Slowly it became clear that things that look like nature are in reality a work of genius. The human touch amplified the natural beauty of the land and transformed it into something out of this world: beautiful, peaceful, and serene.
I spent hours in the garden. When I was about to leave, my floodgates were open. I started crying. Mom, I love you; please forgive me.
Puzzle. A boy fell off of a 30 meter ladder, but didn't get hurt. Why not?

I was very happy to hang out with my oldest coauthor, Richard Guy, at the Gathering for Gardner conference in Atlanta in April 2018. By the way, Richard Guy is 101 years old.
John Conway came to the 2017 MOVES conference and told me that he wanted to talk to me about subprime fibs. The subprime Fibonacci sequence was invented by John Conway, and I wrote a paper about it. The paper, Conway's Subprime Fibonacci Sequences, wasn't written with John, but rather with Richard Guy and Julian Salazar, and is published in Mathematics Magazine.
I wanted to visit my friend Julia, who lives in Princeton, and this was a good opportunity to discuss the mysteries of subprime fibs with John. On my second day in Princeton, I came to the math department around 3:00 pm carrying some apples. John never goes out for lunch, as he has trouble walking, so he is always hungry by the end of his work day. Thus, each time I go visit him, I come with food. We have very different tastes in apples: unlike me, he likes his apples unwashed.
Anyway, by the time I arrived to the department, John had already left. This was somewhat unusual, so I called him. He sounded weird and not very coherent, as if he wasn't feeling well. Considering also that he had left early, I started to worry. Unfortunately, there was a lot of background noise during our conversation and I only understood that he was at a pizza place. John walks very slowly, so he couldn't have gone too far away from campus. I found him in the second pizza place I checked. It was Tiger's Pizza. He told me that he felt very sleepy and tired. However, I was gratified to see how much having an interested listener gave him energy. He started telling me stories of his trip to Germany a long time ago. He had already eaten, but decided to have some more fries. As a perfect gentleman he offered me some, but I didn't want any.
At some point he dropped a couple of fries on the floor. He tried to reach them and I jumped to help. That was a mistake. I actually know that he likes proving to me and to himself that he can do stuff independently. He accepts my help when I am subtle about it, or when it is unavoidable. Anyway, he looked at me angrily and I backed off. He picked up his fries from the floor and ate them.

I liked his T-shirt and tried to take a picture of it. As you can see, I am no photographer. The T-shirt shows a test question: Name the triangles. Then it features three triangles: an equilateral, isosceles, and right. It also provides someone's answers to this naming test: Geoffrey, Frederick, Eugene.
John asked me if I am more scared of Donald Trump or Kim Jong Un. We agreed that Trump is scarier. At this time he seemed his usual self.
I offered John a ride home, as I do whenever I visit him. He was very glad as he felt very tired. He started to get up. This time, I remembered not to try to help. He couldn't get up, I waited. He tried to push his weight off the table top, but the table was wobbly. I leaned on the table, as if to rest. We often play this sort of game in which he welcomes my help as long as we both pretend that I'm not helping.
My car was a block away and he wanted to walk the block. But after making two steps out of the pizzeria he changed his mind and asked me to bring the car to him. This was the first time ever. This visit he was so much worse than ever before.
On the drive to his place, he gave me a puzzle:
John's puzzle. Given a Mebius strip with a hole, how do you embed it in 3-D so that the two circular borders of the surface are equivalent?
I dropped him off at his house and offered to walk him to the door. He refused. I sat in my car and watched him walking very slowly along his path. I had this sinking feeling in my gut that I was seeing John for the last time. I drove away, once he disappeared behind his door.
On my way back to Boston I visited my friend Vitaly in East Brunswick, and the next day my high school friend Olga in Edison. In Edison, my car started beeping and I panicked. I was far away from home, and didn't want to be stuck in NJ. I started to look for the source of the sound. It was John's phone. As always, my gut feeling deceived me: I had to go back to Princeton.
I drove back to John's apartment. His door was unlocked and I entered. He was resting in bed. He was greatly annoyed at being disturbed. I explained the reason, and gave him his phone. He took the phone and said, "Off you go." I had this sinking feeling in my gut that these words would be the last words that I would hear from John.
Here is the crypto word search I designed as a gift exchange for G4G13 (Gathering for Gardner). The submitted file is here: Crypto Word Search.
A B C D E F G H C I F B B C D I J K L A J C I F M A C K N O O N F B I F J O P P Q G H F A R K J B
The words are: ART IDEA MAGIC MATH NOTE PI PROBLEM PUZZLE RIDDLE TRICK.
This is a math blog, but from time to time, I write about other things. Today I have something to say about puns, which I adore.
I also like gym, but rarely go there: it doesn't work out. I stopped using stairs, because they are up to something. I wanted to learn how to juggle, but I don't have the balls to do it.
I work at MIT, the work place with the best dam mascot: Tim the Beaver. My salary is not big, and I stopped saving money after I lost interest. I'm no photographer, but I have pictured myself outside of MIT too. I am a mathematician, which is the most spiritual profession: I am very comfortable with higher powers. I praise myself on great ability to think outside the box: it is mostly due to my claustrophobia. I am also a bit of a philosopher: I can go on talking about infinity forever.
I would love to tell you a joke. I recently heard a good one about amnesia, but I forgot how it goes.
My biggest problem is with English. So what if I don't know what apocalypse means? It's not the end of the world!
I never get tired of puns and here is my list of pun puzzles from the MIT Mystery Hunt:
* * *
Business plan:
* * *
* * *
A cafe patron ordered a pastry, then changed his mind and replaced it with a cup of coffee. When he finished his coffee, he started leaving without paying. The waiter approached him:
—You didn't pay for coffee!
—But I had it instead of the pastry.
—You didn't pay for the pastry either!
—But I didn't have the pastry.
* * *
At a farmers market stand there is a sign: 1 melon—3 dollars, 3 melons—10 dollars. A client requests one melon and pays 3 dollars, then repeats the procedure two more times. Then he says: "I bought three melons for 9 dollars, while you are trying to sell them for 10 dollars. This is really stupid." The farmer talks to himself: This happens all the time: they buy three melons instead of one, and try to teach me how to make money.
* * *
If the government listens in on my phone conversations, should they be paying half of my phone bill?
* * *
To get to free downloads, please, enter your credit card number.
* * *
The biggest lie of the century, "I have read and agree to the terms of ..."
* * * (submitted by Sam Steingold)
Ignorance: If your poker opponent got lucky cards four times in a row, he must get lousy cards now.
Knowledge: Nope, the deals are independent; prior observations have no bearing on the next deal.
Wisdom: The opponent is cheating; get away from the table now!
I recently posted two geometry problems. Now is the time for solutions:
Problem 1. Is it possible to put positive numbers at the vertices of a triangle so that the sum of two numbers at the ends of each side is equal to the length of the side?
One might guess that the following numbers work: (a+b-c)/2, (b+c-a)/2 and (c+a-b)/2, where a, b, and c are the side lengths. But there exists a geometric solution: Construct the incircle. The tangent points divide each side into two segment, so that the lengths of the segments ending at the same vertex are the same. Assigning this length to the vertex solves the problem. Surprisingly, or not surprisingly, this solution gives the same answer as above.
Problem 2. Prove that it is possible to assign a number to every edge of a tetrahedron so that the sum of the three numbers on the edges of every face is equal to the area of the face.
The problem is under-constrained: there are six sides and four faces. There should be many solutions. But the solution for the first problem suggests a similar idea for the second problem: Construct the inscribed sphere. Connect a tangent point on each face to the three vertices on the same face. This way each face is divided into three triangles. Moreover, the lengths of the segments connecting the tangent points to a vertex are the same. Therefore, two triangles sharing the same edge are congruent and thus have the same area. Assigning this area to each edge solves the problem.
There are many solutions to the second problem. I wonder if for each solution we can find a point on each face, so that the segments connecting these points to vertices divide the faces into three triangles in such a way that triangles sharing an edge are congruent. What would be a geometric meaning of these four points?
I was on the writing team for the 2018 MIT Mystery Hunt. I am pleased that the hunt got very positive reviews from the participants. I spent tons of hours working on the hunt and it is good that folks liked it. I edited and tested a lot of puzzles. Here is my review of these year's puzzles that are math-related.
I already posted an essay about the puzzles I wrote myself. Four of my five puzzles are math-related, so I am including them below for completeness. I will mention the topic of each puzzle unless it is a spoiler.
I start with Nikoli-type puzzles. Four elegant Nikoli-type puzzles were written or cowritten by Denis Auroux. In all of them the rules of the logic are stated at the beginning. That means the logic part doesn't contain a mystery and can be solved directly.
There were several puzzles that were very mathematical.
There were also some math-related or computer-sciency puzzles.
There were also several decryption puzzles:
Here is a famous math problem I never before wrote about:
Puzzle. Five pirates discovered a treasure of 100 gold coins. They decide to split the coins using the following scheme. The most senior pirate proposes how to share the coins, and all the pirates vote for or against it. If 50% or more of the pirates vote for it, then the coins will be shared that way. Otherwise, the pirate proposing the scheme will be thrown overboard, and the process is repeated with the next most senior pirate making a proposal.
As pirates tend to be a bloodthirsty bunch, if a pirate would get the same number of coins whether he votes for or against a proposal, he will vote against so that the pirate who proposed the plan will be thrown overboard. Assuming that all five pirates are intelligent, rational, greedy, and do not wish to die, how will the coins be distributed?
You can find the solution in many places including Wikipedia's Pirate game. The answer is surprising: the most senior pirate gets 98 coins, and the third and the fifth pirates by seniority get one coin each. I always hated this puzzle, but never bothered to think through and figure out why. Now I know.
This puzzle emphasizes the flaws of majority voting. The procedure is purely democratic, but it results in extreme inequality.
That means a democracy needs to have a mechanism to prohibit the president from blatantly benefiting himself. With our current president these mechanisms stopped working. Given that Trump does everything to enrich himself, the pirates puzzle tells us what to expect in the near future.
We, Americans, will lose everything: money, clean air and water, national parks, future climate, health, social security, and so on, while Trump will make money.
I was on the writing team of this year's hunt, which was based on the movie "Inside Out." One of our goals was to create an easy first round to allow small teams to have a full hunt experience. Our first round consisted of 34 puzzles related to five basic emotions: joy, sadness, disgust, fear, and anger. Each emotion had its own meta puzzle. And the round had a meta-meta puzzle and a runaround. As I tend to write easy puzzles, I contributed three puzzles to this emotions round. The puzzles had references to corresponding emotions that were not needed for the solve path. They were inserted there for flavor.
I also wrote another easy puzzle called A Tribute: 2010-2017 (jointly with Justin Melvin, Wesley Graybill, and Robin Diets ). Though the puzzle is easy, it is useful in solving it to be familiar with the MIT mystery hunt. This is why the puzzle didn't fit the first emotions round.
I also wrote a very difficult puzzle called Murder at the Asylum. This is a monstrosity about liars and truth-tellers.
In mathematics one of the most important questions is why. Let us consider a problem:
Problem. A number has three hundred ones and three hundred zeroes. Can it be a square?
The solution goes like this. Consider divisibility of this number by 9. The sum of the digits is 300. That means the number is divisible by 3, but not by 9. Therefore, it can't be a square.
Why do we consider divisibility by 9? The divisibility by 9 is a very powerful tool, but why was it the first thing that came to my mind? The divisibility by 9 doesn't depend on the order of the digits. Whenever I see a problem where the question talks about digits that can be in any order, the first tool to use is the divisibility by 9.
The why question, is very important in mathematics. But it is also very important in life. It took me many years to start asking why people did this or that. I remember my mom was visiting me in the US. Every time I came back from work, she complained that she was tired. Why? Because she did the laundry in the bath tub. She wouldn't use my washing machine, because she didn't have such a thing in Russia. I promised her that I'd do the laundry myself when there was a sufficient pile. However, she insisted that the dirty clothes annoyed her. I would point that my water bill went up. And so on.
We argued like this every day. We were both frustrated. Then I asked myself why. Why does she do the laundry? The answer was there. She wanted to be helpful. I calmed down and stopped arguing with her. I sucked it up and paid the water bills. Her time with me turned into the most harmonious visit we ever had. Unfortunately, it was the last.
Puzzle. Alice, Bob, and Charlie are at Alice's house. They are going to Bob's house which is 33 miles away. They have a 2-seat scooter which rides at 25 miles per hour with 1 rider on it; or, at 20 miles per hour with 2 riders. Each of the 3 friends walks at 5 miles per hour. How fast can all three of them make it to Bob's house?
* * * (submitted by Sam Steingold)
I can count to 1023 on my 10 fingers. The rudest number is 132.
* * *
I kept forgetting my password, so I changed it to "incorrect". Now, when I make a mistake during login, my computer reminds me: "Your password is incorrect."
* * *
—You promised me 8% interest, and in reality it is 2%.
—2 is 8—to some degree.
* * * (submitted by Sam Steingold)
Quantum entanglement is simple: when you have a pair of socks and you put one of them on your left foot, the other one becomes the "right sock," no matter where it is located in the universe.
* * *
Teacher:
—I keep telling my students that one half can't be larger or smaller than the other. Still the larger half of my class doesn't get it.
This famous trick puzzle is very old:
Puzzle. The professor is watching across a field how the son of the professor's father is fighting with the father of the professor's son. How is this possible?
This puzzle is tricky only because of gender-bias. Most people assume that the professor is male and miss the obvious intended solution, in which a female professor is watching her brother fighting with her husband.
I just gave this problem on a test. Here are other answers that I received.
Years ago people couldn't figure out this puzzle at all. So there has been progress. I was glad that my students suggested so many ideas that work. Nonetheless, many of them revealed their gender-bias by initially assuming that the professor is a man.
I can't wait until this puzzle stops being tricky.
Puzzle. There are five houses of different colors next to each other equally spaced on the same road. In each house lives a man of a different profession.
Who lives in the white house?
Correction Nov 11, 2017. Replaced "the same distance from" with "halfway between" to eliminate the possibility of the plumber living in the yellow house. Thank you to my readers for catching this mistake and to Smylers for suggesting a correction.
I do not remember where I saw this problem.
Problem. Invent a connected shape made out of squares on the square grid that cannot be cut into dominoes (rectangles with sides 1 and 2), but if you add a domino to the shape then you can cut the new bigger shape.
This problem reminds me of another famous and beautiful domino-covering problem.
Problem. Two opposite corner squares are cut out from the 8 by 8 square board. Can you cover the remaining shape with dominoes?
The solution to the second problem is to color the shape as a chess board and check that the number of black and white squares is not the same.
What is interesting about the first problem is that it passes the color test. It made me wonder: Is there a way to characterize the shapes on a square grid that pass the color test, but still can't be covered in dominoes?
* * *
Don't anthropomorphize computers: They don't like it.
* * *
I do not have dreams any more. What did I do wrong to make them delete my account?
* * *
How to restore justice: Create a folder named Justice. Delete it. Go to the trash bin and click restore.
* * *
An asocial network: When you sign up, you are friends with everyone. Then you send un-friend requests.
I already wrote about two puzzles that Derek Kisman made for the 2013 MIT Mystery Hunt. The first puzzle is now called the Fractal Word Search. It is available on the Hunt website under its name In the Details. I posted one essay about the puzzle and another one describing its solution. The second puzzle, 50/50, is considered one of the most difficult hunt puzzles ever. Unfortunately, the puzzle is not available, but my description of it is.
Today let's look at the third puzzle Derek made for the 2013 Hunt, building on an idea from Tom Yue. This is a non-mathematical crossword puzzle. Derek tends to write multi-layered puzzles: You think you've got the answer, but the answer you've got is actually a hint for the next step.
Often multi-layered puzzles get solvers frustrated, but the previous paragraph is a hint in itself. If you expect the difficulty, you might appreciate the fantastic beauty of this puzzle.
Welcome to Ex Post Facto.
Every time I visit Princeton, or otherwise am in the same city as my friend John Conway, I invite him for lunch or dinner. I have this rule for myself: I invite, I pay. If we are in the same place for several meals we alternate paying. Once John Conway complained that our tradition is not fair to me. From time to time we have an odd number of meals per visit and I end up paying more. I do not trust my memory, so I prefer simplicity. I resisted any change to our tradition. We broke the tradition only once, but that is a story for another day.
Let's discuss the mathematical way of paying for meals. Many people suggest using the Thue-Morse sequence instead of the alternating sequence of taking turns. When you alternate, you use the sequence ABABAB…. If this is the order of paying for things, the sequence gives advantage to the second person. So the suggestion is to take turns taking turns: ABBAABBAABBA…. If you are a nerd like me, you wouldn't stop here. This new rule can also give a potential advantage to one person, so we should take turns taking turns taking turns. Continuing this to infinity we get the Thue-Morse sequence: ABBABAABBAABABBA… The next 2n letters are generated from the first 2n by swapping A and B. Some even call this sequence a fair-share sequence.
Should I go ahead and implement this sequence each time I cross paths with John Conway? Actually, the fairness of this sequence is overrated. I probably have 2 or 3 meals with John per trip. If I pay first every time, this sequence will give me an advantage. It only makes sense to use it if there is a very long stretch of meals. This could happen, for example, if we end up living in the same city. But in this case, the alternating sequence is not so bad either, and is much simpler.
Many people suggest another use for this sequence. Suppose you are divorcing and dividing a huge pile of your possessions. A wrong way to do it is to take turns. First Alice choses a piece she wants, then Bob, then Alice, and so on. Alice has the advantage as the first person to choose. An alternative suggestion I hear in different places, for example from standupmaths, is to use the Thue-Morse sequence. I don't like this suggestion either. If Alice and Bob value their stuff differently, there is a better algorithm, called the Knaster inheritance procedure, that allows each of them to think they are getting more than a half. If both of them have the same value for each piece, then the Thue-Morse sequence might not be good either. Suppose one of the pieces they are dividing is worth more than everything else put together. Then the only reasonable way to take turns is ABBBB….
The beauty of the Thue-Morse sequence is that it works very well if there are a lot of items and their consecutive prices form a power function of a small degree k, such as a square or a cube function. After 2k+1 turns made according to this sequence, Alice and Bob will have a tie. You might think that if the sequence of prices doesn't grow very fast, then using the Thue-Morse sequence is okay.
Not so fast. Here is the sequence of prices that I specifically constructed for this purpose: 5,4,4,4,3,3,3,2,2,2,2,1,1,0,0,0. The rule is: every time a turn in the Thue-Morse sequence switches from A to B, the value goes down by 1. Alice gets an extra 1 every time she is in the odd position. This is exactly half of her turns. That is every four turns, she gets an extra 1.
If the prices grow faster than a power, then the sequence doesn't work either. Suppose your pieces have values that form a Fibonacci sequence. Take a look at what happens after seven turns. Alice will have pieces priced Fn + Fn-3 + Fn-5 + Fn-6. Bob will have Fn-1 + Fn-2 + Fn-4. We see that Alice gets more by Fn-3. This value is bigger than the value of all the leftovers together.
I suggest a different way to divide the Fibonacci-priced possessions. If Alice takes the first piece, then Bob should take two next pieces to tie with Alice. So the sequence might be ABBABBABB…. I can combine this idea with flipping turns. So we start with a triple ABB, then switch to BAA. After that we can continue and flip the whole thing: ABBBAABAAABB. Then we flip the whole thing again. And again and again. At the end we get a sequence that I decided to call the Fibonacci fair-share sequence.
I leave you with an exercise. Describe the Tribonacci fair-share sequence.
A while ago I posted my second favorite problem from the 2015 All-Russian Math Olympiad:
Problem. A coin collector has 100 coins that look identical. He knows that 30 of the coins are genuine and 70 fake. He also knows that all the genuine coins weigh the same and all the fake coins have different weights, and every fake coin is heavier than a genuine coin. He doesn't know the exact weights though. He has a balance scale without weights that he can use to compare the weights of two groups with the same number of coins. What is the smallest number of weighings the collector needs to guarantee finding at least one genuine coin?
Now it's solution time. First we show that we can do this in 70 weighings. The strategy is to compare one coin against one coin. If the scale balances, we are lucky and can stop, because that means we have found two real coins. If the scale is unbalanced, the heavier coin is definitely fake and we can remove it from consideration. In the worst case, we will do 70 unbalanced weighings that allow us to remove all the fake coins, and we will find all the real coins.
The more difficult part is to show that 69 weighings do not guarantee finding the real coin. We do it by contradiction. Suppose the weights are such that the real coin weighs 1 gram and the i-th fake coin weighs 100i grams. That means whatever coins we put on the scale, the heaviest pan is the pan that has the fake coin with the largest index among the fake coins on the scale.
Suppose there is a strategy to find a real coin in 69 weighings. Given this strategy, we produce an example designed for this strategy, so that the weighings are consistent, but the collector cannot find a real coin.
For the first weighing we assign the heaviest weight, 10070 to one of the coins on the scale and claim that the pan with this coin is heavier. We continue recursively. If a weighing has the coins with assigned weights, we pick the heaviest coin on the pans and claim that the corresponding pan is heavier. If there are no coins with assigned weights on pans, we pick any coin on the pans, assigned the largest available weight to it and claim that the corresponding pan is heavier.
After 69 weighings, not more than 69 coins have assigned weights, while all the weighings are consistent. The rest of the coins can have any of the leftover weights. For example, any of the rest of the coins can weigh 100 grams. That means that there is no coin that is guaranteed to be real.
I stumbled upon a couple of problems that I like while scanning the Russian website of Math Festival in Moscow 2014. The problems are for 7 graders.
Problem. Inside a 5-by-8 rectangle, Bart draws closed paths that follow diagonals of 1-by-2 rectangles. Find the longest possible path.
This problem is really very difficult. The competition organizers offered an extra point for every diagonal on top of 16. The official solution has 24 diagonals, but no proof that it's the longest. I'm not sure anyone knows if it is the longest.
Here is another problem:
Problem. Alice and Bob are playing a game. They start with two numbers: 2014 and 2015. In one move a player can do one of two things:The winner is the person who is the first to get a one-digit number. Assuming that Alice starts, who wins?
- subtract one of the numbers by one of the non-zero digits in any of the two numbers or,
- divide one number by two if the number is even.

The year is 1994. The man on the left is my first husband, Alexander Goncharov. Although we were out of touch for a decade, when I married my third husband, Joseph Bernstein (on the right), Goncharov started visiting us. It wasn't me he was interested in: he wanted to talk mathematics with my husband. I found this situation hilarious, so I took this photo.
But that's not all. My second husband, Andrey Radul, is not in the picture. But all four of us were students of Israel Gelfand. In short, my three ex-husbands and I are mathematical siblings — that is, we are all one big happy mathematical family.

The Best Writing on Mathematics 2016 is out. I am happy that my paper The Pioneering Role of the Sierpinski Gasket is included. The paper is written jointly with my high-school students Eric Nie and Alok Puranik as our PRIMES-2014 project.
At the end of the book there is a short list of notable writings that were considered but didn't make it. The "short" list is actually a dozen pages long. And it includes two more papers of mine:
To continue bragging, I want to mention that my paper A Line of Sages was on the short list for 2015 volume. And my paper Conway's Wizards was included in the 2014 volume.

I like Odd-One-Out puzzles that are ambiguous. That is why I bought the book Which One Doesn't Belong? Look at the cover: which is the odd one out? The book doesn't include answers, but it has nine more examples in each of which there are several possible odd-one-outs.
I married an American citizen and moved to the US in 1990. At the time I was a very patriotic Russian. It took me a year of pain to realize that some of my ideas had been influenced by Soviet propaganda. After I washed away the brainwashing, I fell in love with the US. For 25 years I thought that America was great. Not anymore.
For the last several months I've been worried as never before in my life. I feel paralyzed and sick. To help myself I decided to put my feelings in words.
World War. My mom was 15 when World War II started. The war affected her entire life, as well as the lives of everyone in the USSR. Every now and then my mom would tell me, "You are lucky that you are already 20 and you haven't witnessed a world war." I moved to the US while my mom stayed back in Russia. From time to time I tell myself something like, "I am lucky that halfway through my expected lifetime, I haven't had to live through a world war." It's been more than 70 years since WWII ended. To maintain the peace is a difficult job. Everything needs to be in balance. Trump is disrupting this balance. I am worried sick that my children or grandchildren will have to witness a major war.
The Red Button. I've noticed that, as a true showman, Trump likes misdirecting attention from things that worry him to fantastic plot twists that he invents. What's the best way to make people forget about his tax returns? It's the nuclear button. Dropping a nuclear bomb some place will divert people from thinking about his tax returns. As his plot twists are escalating, is he crazy enough to push the button?
Climate. The year 2014 was the warmest on record. The year 2015 was even warmer. And last year, 2016, was even warmer than that. I remember Vladimir Arnold's class on differential equations. He talked about a painting that had been hanging on a wall for 20 years. Then it unexpectedly fell off. Mathematics can explain how such catastrophic events can happen. I keep thinking about our Earth: melting ice, dead reefs, fish eating plastic, and so much more. My grandchildren might not be able to enjoy beaches and forests the way I did. What if, like the fallen painting, the Earth can spiral out of control and completely deteriorate? But Trump is ignoring the climate issues. Does he care about our grandchildren? I am horrified that Trump's policies will push climate catastrophe beyond the point of no return.
The Truth. Wiretapping is not wiretapping. Phony jobs numbers stopped being phony as soon as Trump decided that he deserved the credit. The news is fake when Trump doesn't like it. Trump is a pathological liar; he assaults the truth. Being a scientist I am in search of truth, and Trump diminishes it. I do not understand why people ignore his lies. Two plus two is four whether you are a democrat, or a republican, or whomever. Facts are facts, alternative facts are lies. I am scared that lies have become acceptable and no one cares about the truth any more.
Russia. I lived in Russia for the first unhappy half of my life, and in the US for the second happy half. I do not want to go back. There is something fishy between Putin and Trump. Whether it is blackmail or money, or both, I do not know the details yet, But Trump is under Putin's influence. Trump didn't win the elections: Putin won. This horrifies me. I do not want to go back to being under Russian rule.
Gender Issues. I grew up in a country where the idea of a good husband was a man who wasn't a drunkard. That wasn't enough for me. I dreamed of a relationship in which there would be an equal division of work, both outside and inside the home. I could not achieve that because in Russian culture both people work full-time and the wife is solely responsible for all the house chores. Moreover, Russia was much poorer than the US: most homes didn't have washing machines; we never heard of disposable diapers; and there were very long lines for milk and other necessities.
The life in USSR was really unfair to women. Most women had a full-time job and several hours of home chores every day. When I moved to the US, I thought I was in paradise. Not only did I have diapers and a washing machine, I was spending a fraction of the time shopping, not to mention that my husband was open to helping me, and didn't mind us paying for the occasional babysitter or cleaner.
For some time I was blind to gender issues in the US because it was so much better. Then I slowly opened my eyes and became aware of the bias. For some years it has felt like gender equity was improving. Now, with a misogynistic president, I feel that the situation might revert to the dark ages. When women are not happy, their children are not happy, and they grow up to be not happy. If the pursuit of happiness is the goal, the life has to be fair to all groups. But Trump insults not only women but also immigrants, Muslims, members of the LGBTQ community, as well as the poor and the sick. The list is so long, that almost everyone is marginalized. This is not a path towards a happy society.
Democracy. Trump attacks the press and attempts to exclude them. Trump has insulted the intelligence community and the courts. He seems to be trying to take more power to the presidency at the expense of the other branches of government. He ignores his conflicts of interest. Trump disregards every rule of democracy and gets away with it. I am horrified that our democracy is dying.
Tax Returns. Trump's tax returns could either exonerate him or prove that he is Putin's puppet. The fact that he is hiding the returns makes me believe that the latter is more probable. Why the Republicans refuse to demand to see his returns is beyond my understanding.
Corruption. Trump does so many unethical things. Most of his decisions as president seem to be governed by Trump trying to get richer. Let us consider his hotel in Azerbaijan—a highly corrupt country. Having lived in a highly corrupt country myself, I know how it works. For example, an Azerbaijani government official who has access to their country's money can make a deal that involves a personal kickback. This means that their government is paying more than necessary for a service or product in order to cover that kickback. This is how national money makes its way into individual pockets. Since all the deals in Azerbaijan are reputed to be like that, I imagine that when Trump built his hotel there, the Trump organization was overpaid in order to cover the bribe to local officials. Will our country become as corrupt as Azerbaijan?
Americans. The biggest shock of the election was that so many people were so gullible and actually voted for Trump. They didn't see that his agenda is focused on his own profit, and that he lies and makes promises he doesn't plan to deliver. It really terrifies me that there are some people who are not gullible but still voted for Trump.
Is there hope?
I recently wrote about my way of playing Nim against a player who doesn't know how to play. If my move starts in an N-position, then I obviously win. If my move starts in a P-position, I would remove one token hoping that more tokens for my opponent means more opportunity for them to make a mistake. But which token to remove? Does it make a difference from which pile I choose?
Consider the position (2,4,6). If I take one token, my opponent has 11 different moves. If I choose one token from the first or the last pile, my opponent needs to get to (1,4,5) not to lose. If I choose one token from the middle pile, my opponent needs to get to (1,3,2) not to lose. But the first possibility is better, because there are more tokens left, which gives me a better chance to have a longer game in case my opponent guesses correctly.
That is the strategy I actually use: I take one token so that the only way for the opponent to win is to take one token too.
This is a good heuristic idea, but to make such a strategy precise we need to know the probability distribution of the moves of my opponent. So let us assume that s/he picks a move uniformly at random. If there are n tokens in a N-position, then there are n − 1 possible moves. At least one of them goes to a P-position. That means my best chance to get on the winning track after the first move is not more than n/(n−1).
If there are 2 or 3 heaps, then the best strategy is to go for the longest game. With this strategy my opponent always has exactly one move to get to a P-position, I win after the first turn with probability n/(n−1). I lose the game with probability 1/(n−1)!!.
Something interesting happens if there are more than three heaps. In this case it is possible to have more than one winning move from a N-position. It is not obvious that I should play the longest game. Consider position (1,3,5,7). If I remove one token, then my opponent has three winning moves to a position with 14 tokens. On the other hand, if I remove 2 tokens from the second or the fourth pile, then my opponent has one good move, though to a position with only 12 tokens. What should I do?
I leave it to my readers to calculate the optimal strategy against a random player starting from position (1,3,5,7).
It is rare when a word equation coincides with a number equation.
Problem. A store sells letter magnets. The same letters cost the same and different letters might not cost the same. The word ONE costs 1 dollar, the word TWO costs 2 dollars, and the word ELEVEN costs 11 dollars. What is the cost of TWELVE?

Alex Bellos wrote a puzzle book Can You Solve My Problems? Ingenious, Perplexing, and Totally Satisfying Math and Logic Puzzles The book contains a mixture of famous puzzles and their solutions. Some of the puzzles are not mathematical in the strictest sense, but still have an appeal for mathematicians. For example, which integer comes up first when you alphabetize all the integers up to a quadrillion?
Recognize the puzzle on that book cover? You're right! That's my Odd One Out puzzle. Doesn't it look great in lights on that billboard in London?
Mine isn't the only terrific puzzle in the book. In fact, one of the puzzles got my special attention as it is related to our current PRIMES polymath project. Here it is:
A Sticky Problem. Dick has a stick. He saws it in two. If the cut is made [uniformly] at random anywhere along the stick, what is the length, on average, of the smaller part?

The beautiful Pascal triangle has been around for many years. Can you say something new about it?
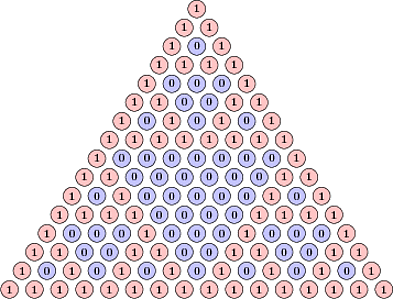
Of course you can. Mathematicians always find new way to look at things. In 2012 RSI student, Kevin Garbe, did some new and cool research related to the triangle. Consider Pascal's triangle modulo 2, see picture which was copied from a stackexchange discussion.
A consecutive block of m digits in one row of the triangle modulo 2 is called an m-block. If you search the triangle you will find that all possible binary strings of length 2 are m-blocks. Will this trend continue? Yes, you can find any possible string of length 3, but it stops there. The blocks you can find are called accessible blocks. So, which blocks of length 4 are not accessible?
There are only two strings that are not accessible: 1101 and 1011. It is not surprising that they are reflections of each other. Pascal's triangle respects mirror symmetry and the answer should be symmetric with respect to reflection.
You can't find these blocks on the picture, but how do we prove that they are not accessible, that is, that you can't ever find them? The following amazing property of the triangle can help. We call a row odd/even, if it corresponds to binomial coefficients of n choose something, where n is an odd/even number. Every odd row has every digit doubled. Moreover, if we take odd rows and replace every double digit with its single self we get back Pascal's triangle. Obviously the two strings 1101 and 1011 can't be parts of odd rows.
What about even rows? The even rows have a similar property: every even-indexed digit is a zero. If you remove these zeros you get back Pascal's triangle. The two strings 1101 and 1011 can't be part of even rows. Therefore, they are not accessible.
The next question is to count the number of inaccessible blocks of a given length: a(n). This and much more was done by Kevin Garbe for his RSI 2012 project. (I was the head mentor of the math projects.) His paper is published on the arxiv. The answer to the question can be found by constructing recurrence relations for odd/even rows. It can be shown that a(2r) = 3a(r) + a(r+1) − 6 and a(2r+1) = 3a(r) + 2a(r+1) − 6. As a result the number of inaccessible blocks of length n is n2 − n + 2. I wonder if there exists a direct proof of this formula without considering odd and even rows separately.
This RSI result was so pretty that it became a question at our entrance PRIMES test for the year 2013. In the test we changed the word accessible to admissible, so that it would be more difficult for applicants to find the research. Besides, Garbe's paper wasn't arxived yet.
The pretty picture above is from the stackexchange, where one of our PRIMES applicants tried to solicit help in solving the test question. What a shame.
I picked four problems that I liked from the Moscow Math Olympiad 2016:
Problem 1. Ten people are sitting around a round table. Some of them are knights who always tell the truth, and some of them are knaves who always lie. Two people said, "Both neighbors of mine are knaves." The other eight people said, "Both neighbors of mine are knights." How many knights might be sitting around the round table?
Problem 2. Today at least three members of the English club came to the club. Following the tradition, each member brought their favorite juice in the amount they plan to drink tonight. By the rules of the club, at any moment any three members of the club can sit at a table and drink from their juice bottles on the condition that they drink the same amount of juice. Prove that all the members can finish their juice bottles tonight if and only if no one brings more than the third of the total juice brought to the club.
Problem 3. Three piles of nuts together contain an even number of nuts. One move consists of moving half of the nuts from a pile with an even number of nuts to one of the other two piles. Prove that no matter what the initial position of nuts, it is possible to collect exactly half of all the nuts in one pile.
Problem 4. N people crossed the river starting from the left bank and using one boat. Each time two people rowed a boat to the right bank and one person returned the boat back to the left bank. Before the crossing each person knew one joke that was different from all the other persons' jokes. While there were two people in the boat, each told the other person all the jokes they knew at the time. For any integer k find the smallest N such that it is possible that after the crossing each person knows at least k more jokes in addition to the one they knew at the start.
Spoiler for Problem 2. I want to mention a beautiful solution to problem 2. Let's divide a circle into n arcs proportionate to the amount of juice members have. Let us inscribe an equilateral triangle into the circle. In a general position the vertices of the triangle point to three distinct people. These are the people who should start drinking juices with the same speed. We rotate the triangle to match the drinking speed, and as soon as the triangle switches the arcs, we switch drinking people correspondingly. After 120 degree rotation all the juices will be finished.
I already posted a funny true story that Smullyan told me when I last visited him. Raymond Smullyan died recently at the age of 97 and my mind keeps coming back to this last visit.
The year was 2012 and I was about to drive back to Boston after my talk at Penn State. Smullyan's place in the Catskills was on the way—sort of. I wanted to call him, but I was apprehensive. Raymond Smullyan had a webpage on which his email was invisible. You could find his email address by looking at the source file or by highlighting empty space at the bottom of the page. Making your contact information invisible sends a mixed message.
While this was a little eccentric, it meant that only people who were smart enough to find it, could access his email address. I already knew his email because he had given it to me along with his witty reply to my blog post about our meeting at the Gathering for Gardner in 2010.
In our personal interactions, he always seemed to like me, so I called Raymond and arranged a visit for the next day around lunch time. When I knocked on his door, no one answered, but the door was open, and since Smullyan was expecting me, I walked right in. "Hello? Anyone there? Hello? Hello?" As I wandered around the house, I saw an open bedroom door and inside Smullyan was sleeping. So I sat down in his library and picked up a book.
When he woke up, he was happy to see me, and he was hungry. He told me that he didn't eat at home, so we should go out together for lunch. I was hungry too, so I happily agreed. Then he said that he wanted to drive. I do not have a poker face, so he saw the fear in me. My only other trip with a nonagenarian driver flashed in front of my eyes. The driver had been Roman Totenberg and it had been the scariest drive I have ever experienced.
I said that I wanted to drive myself. Annoyed, Raymond asked me if I was afraid of him taking the wheel. I told him that I have severe motion sickness and always prefer to drive myself. Raymond could see that I was telling the truth. I got the impression that he was actually relieved when he agreed to go in my car.
We went to Selena's Diner. He took out playing cards with which he showed me magic tricks. I showed him some tricks too. This was probably a bad move as he abandoned me to go to the neighboring table to show his magic tricks to a couple of young girls. They were horrified at first"his unruly hair, his over-the-top energy, his ebullient behavior"but between me and the waitress, we quickly reassured them. The girls enjoyed the tricks, and I enjoyed my visit.
Like many people, I was appalled by Trump's immigration ban. On the Internet I found many essays that explained that he did not include in the ban those majority-Muslim countries in which he has business interests. See for example, an article at Forbes with a nice map, and an article at NPR.
Now the countries that are excluded are motivated to continue to support Trump's businesses, and to offer him bribes and good deals in exchange for staying out of the ban. The countries on the list are also motivated to approach Trump and offer him a sweet business deal.
So even if the courts stopped the ban, he has already succeeded in showing every country in the world that to be on his good side requires that they pay up. And China got the hint and granted Trump a trademark he's been seeking for a decade.
Looks like Trump's vision of a great America is a very rich Mr Trump.
I recently posted the following puzzle:
Puzzle. We have 32n identical-looking coins. One of the coins is fake and lighter than the other coins, which all are real. We also have three scales: two normal and one random. Find the fake coin in the smallest total number of weighings.
Here is my son Sergei's solution. Divide the coins into nine groups of equal size and number the groups in ternary: 00, 01, 02, 10, 11, 12, 20, 21, and 22. On each scale we put three groups versus three groups. On the first scale we compare the three groups that start with 1 with the three groups that start with 2. For the second scale we do the same using the last digit instead of the first one, and for the third scale we use the sum of two digits modulo 3. Any pair of scales, if they are assumed to be normal, would point to one out of nine groups as the group containing the fake coin.
If all three pairs of scales agree on one group, then this is the group containing the fake coin. Thus in three weighings, we reduce the number of groups of coins by a factor of nine. If the pairs of scales do not agree, then the random scale produced a wrong weighing and thus can be found out. How do we do that? We have three out of nine groups of coins each of which might contain the fake coin. We compare two of the groups on all three scales. This way we know exactly which group contains the fake coin and, consequently, which scale generated a wrong weighing. If we know the random scale, we can speed up the rest of the process of finding the fake coin. Thus in the worst case we require 3n+3 weighings.
The big idea here is that as soon as the random scale shows a wrong weighing result it can be found out. So in the worst case, the random scale behaves as a normal scale and messes things up at the very end. Sergei's solution can be improved to 3n+1 weighings. Can you do that?
The improved solution is written in a paper Взвешивания на "хитрых весах" (in Russian) by Konstantin Knop, that is published in Математика в школе 2009-2. The paper contains an even stronger solution that provides a better asymptotics.
The first time I visited the US was in 1990 at the invitation of an old friend, Joseph Bernstein. After my arrival Joseph proposed and I accepted, but my essay is not about that.
Joseph reintroduced me to his daughter, Mira, who was then in her late teens. I was struck by Mira's charm. I had never before met teenagers like her. Of course, Joseph got points for that as I was hoping to have a child with him. When I moved to the US I met some other kids who were also incredibly charming. It was too late to take points away from Joseph, but it made me realize what a huge difference there was between Soviet and American teenagers. American teenagers were happier, more relaxed, better mannered, and less cynical than Soviet ones.
My oldest son, Alexey, was born in the USSR and moved to the US when he was eight. One unremarkable day when he was in middle school (Baker public school in Brookline), the principle invited me for a chat. I came to the school very worried. The principal explained to me that there was a kid who was bugging Alexey and Alexey pushed him back with a pencil. While the principal proceeded to explain the dangers of a pencil, I tuned out. I needed all my energy to conceal my happy smile. This was one of the happiest moments of my life in the US. What a great country I live in where the biggest worry of a principal in a middle school is the waving of a pencil! I remembered Alexey's prestigious school in Moscow. They had fights every day that resulted in bloody noses and lost teeth. When I complained to his Russian teacher, she told me that it was not her job to supervise children during big breaks. Plus the children needed to learn to be tough. No wonder American children are happier.
I was wondering if there were any advantages to a Soviet upbringing. For one thing, Soviet kids grow up earlier and are less naive. They are more prepared for harsh realities than those American kids who are privileged.
Naive children grow up into naive adults. Naive adults become naive presidents. I watched with pain as naive Bush ("I looked the man in the eye. I found him to be very straightforward and trustworthy.") and naive Obama (Russian reset) misunderstood and underestimated Putin.
Putin is (and, according to Forbes Magazine, has been for the last four years) the most powerful person in the world. Even though the US kept its distance from Russia, he was able to manipulate us from afar. Now that Trump wants to be close to Putin, the manipulation will be even easier. Putin is better at this game. He will win and we will lose.
May 5 of 1955 can be written as 5/5/55. How many times during the 20th century the date in the format month day and the last two digits of the year can be written with the same digit?

I had a distant relative Alla, who was brought up by a single mother, who died in a car crash when the girl was in her early teens. Alla was becoming a sweet and pleasant teenager; she was taken in by her aunt after the accident. Very soon the aunt started complaining that Alla was turning into a cheater and a thief. The aunt found a therapist for Alla, who explained that Alla was stealing for a reason. Because the world had unfairly stolen her mother, Alla felt entitled to compensation in the form of jewelry, money, and other luxuries.
I was reminded of Alla's story when I was reading The (Honest) Truth About Dishonesty: How We Lie to Everyone—Especially Ourselves by Dan Ariely. Ariely discusses a wide range of reasons why honest people cheat. But to me he neglects to look at the most prominent reason. Often honest people cheat when they feel justified and entitled to do so.
One of Ariely’s experiments went like this. One group was asked to write a text avoiding letters x and z. The other group was asked to write a text avoiding letters a and n. The second task is way more difficult and requires more energy. After the tasks were completed the participants were given a test in which they had a chance to cheat. For this experiment, the participants were compensated financially according to the number of questions they solved. Not surprisingly, the second group cheated more. The book concludes that when people are tired, their guard goes down and they cheat more. I do not argue with this conclusion, but I think another reason also contributes to cheating. Have you ever tried to write a text without using the letters a and n? I did:
I should try it here. But this is so difficult. I give up.
My son, Alexey, was way better than me:
First, God brought forth the sky with the world. The world existed without form. Gloom covered the deep. The Spirit of God hovered over the fluids. Quoth God: let there be light. Thus light existed.
Fun as it is, this is cruel and unusual punishment. The request is more difficult than most people expect at an experiment. It could be that participants cheated not only because their capacity for honesty was depleted, but because they felt entitled to more money because the challenge was so difficult.
In another experiment, the participants received a high-fashion brand of sunglasses before the test. Some of them were told that the sunglasses were a cheap imitation of the luxury brand (when they really were not). This group cheated more than the group who thought that they got a real thing. The book concludes that wearing fake sunglasses makes people feel that they themselves are fake and so they care less about their honor. Unfortunately, the book doesn't explain in detail what was actually promised. It looks like the participants were promised high-fashion sunglasses. In this case, the fake group would have felt deceived and might have felt more justified to cheat.
Dear Dan Ariely: May I suggest the following experiment. Invite people and promise them some money for a 15-minute task. Pay them the promised minimum and give them a test through which they can earn more. Construct it so that they can earn a lot more if they cheat. Then make the non-control group wait for half an hour. If I were in this group, I would have felt that I am owed for the total of 45 minutes—three times more than what I was promised. I do not know if I would cheat or just leave, but I wouldn't be surprised that in this group people would cheat more than in the control group.
If like me, you fancy Raymond Smullyan and his books, then you've heard about knights and knaves. Knights always tell the truth and knaves always lie. In addition to knights and knaves, there are normal people who sometimes tell the truth and sometimes lie. Here is a puzzle.
Puzzle. How, in one sentence, can a normal person prove that they are normal?
We can draw a parallel between people and coins. We can say that knights correspond to real coins, and knaves to fake coins that are lighter than real ones. Inspired by normal people, my coauthor Konstantin Knop invented chameleon coins. Chameleon coins can change their weight and behave like real or fake coins. I just wrote a post about chameleon coins.
Normal people are too unpredictable: they can consistently pretend to be knights or knaves. So logicians invented a simpler type of person, one who switches from telling the truth in one sentence to a lie in the next and then back to the truth. Such people are called alternators. Here is another puzzle:
Puzzle. You meet a person who is one of the three types: a knight, a knave, or an alternator. In two questions, find out which type they are.
Continuing a parallel between people and coins we can define alternator coins: the coins that switch their weight each time they are on the scale from weighing as much as real ones to weighing as much as fake ones. For the purposes of this essay, we assume that the fake coins are lighter than real ones. Unlike the chameleon coin, which might never reveal itself by always pretending to be real, the alternators can always be found. How do you find a single alternator among many real coins? There is a simple strategy: repeat every weighing twice. This strategy allows us to find an alternator among 9 coins in four weighings. Can we do better?
I used the alternator coins as a research project for my PRIMES STEP program where we do math research with students in seventh and eighth grade. The students started the alternator project and immediately discovered the strategy above. The next step is to describe a better strategy. For example, what is the maximum number of coins containing one alternator such that the alternator can always be found in four weighings?
But first we count possible outcomes. Suppose there is a strategy that finds an alternator. In this strategy we can't have two unbalanced weighings in a row. To prove that, let us suppose there was an unbalanced weighing. Then the alternator switches its weight to a real coin and whether or not the alternator is on the scale, the next weighing must balance. The beauty of it is that given a strategy each outcome has to point to a particular coin as an alternator. That means the number of outcomes bounds the total number of coins that can be processed.
Counting the number of possible outcomes that do not have two unbalances in row is a matter of solving a recurrence, which I leave to the readers to find. The result is Jacobshtal numbers: the most beautiful sequence you might never have heard of. For example, the total number of possible outcomes of four weighings is 11. Since each outcome of a strategy needs to point to a coin, the total number of coins that can be processed in four weighings is not more than 11. But 11 is better than 9 in our previous strategy. Can we process 11 coins in four weighings? Yes, we can. I will describe the first part of the strategy.
So we have 11 coins, one of which is an alternator. In the first weighing we compare 5 coins against 5 coins. If the weighing unbalances, the alternator is on a lighter pan. Our problem is reduced to finding the alternator among five coins when we know that it is in the real state. If the weighing balances, then we know that if the alternator is among the coins on the scale it must now be in the light state. For the second weighting, we pick two sets of three coins out of this ten coins and compare them against each other. Notice that 3 is a Jacobsthal number, and 5, the number of coins outside the scale, is also a Jacobsthal number. If the second weighing balances, the alternator must be among 5 coins outside the scale. All but one of these coins are in the light state, and I leave it to the readers to finish the strategy. If the weighing unbalances, we need to find the alternator among 3 coins that are in the real state now. This can be done in two weighings, and again the readers are to the rescue.
It appears that Jacobsthal numbers provide the exact lower bound of the number of coins that can be processed. This is what my middle-schoolers discovered and proved. We wrote a paper on the subject. The strategy in the paper is adaptive. That means it changes depending on the results of the previous weighings. Can we find an oblivious strategy? I will tell you in later posts.
Suppose we have 3n identical-looking coins. One of the coins is fake and lighter than the other coins which all are real. We also have a random scale. That is a scale that at each weighing behaves randomly. Find the fake coin in the smallest number of weighings. Oops! That won't work! It is impossible to find the fake coin. The scale can consistently misbehave in such a way as to blame a specific real coin for being fake.
Let's try something else. Suppose we have two scales: one normal and one random. Find the fake coin.
What am I thinking? The normal scale can point to one coin and the random scale can point to another coin and we are in a "she said, he said" situation which we can't resolve.
Now, in my final try, I'll make it right. We actually have three scales, one of which is random. So here we go, with thanks to my son Sergei for giving me this puzzle:
Puzzle. We have 3n identical-looking coins. One of the coins is fake and lighter than the other coins, which all are real. We also have three scales: two normal and one random. Find the fake coin in the smallest total number of weighings.
Let's start with this strategy: repeat every weighing on all three scales and have a majority vote. At least two of the scales will agree, thus pointing to the true result. This way we can use a divide-into-three-equal-groups strategy for one scale to find the fake coin. It will require 3n weighings.
Can we do better? Of course, we can. We can repeat every weighing on two scales. If they agree we do not need the third scale. If they do not agree, one of the scales is random and lying, and we can repeat the weighing on the third scale to "out" the random scale. After we identify one normal scale, the process goes faster. In the worst case we will need 2n + 1 weighings.
Can we do even better? Yes, we can. I will leave it to the readers to find a beautiful solution that is asymptotically better than the previous one.
Update on Dec 24, 2016. The total number of coins should be 32n, not 3n. We are looking at the worst case scenario, when the random scale is adversarial.
We all have played with problems in which we had real coins and fake (counterfeit) coins. For this post I assume that the fake coins are always lighter than the real coins. My coauthor Konstantin Knop invented a new type of a coin: a chameleon coin. This coin can mimic a fake or a real coin. It can also choose independently which coin to mimic for each weighing on a balance scale.
You cannot find the chameleon coin in a mix with real coins if it does not want to be found, because it can consistently behave as a real coin. Let's add classic fake coins to the mix, the ones that are lighter. Still the task of identifying the chameleons using a balance scale cannot be achieved: the chameleons can pretend to be fake coins. We can't identify the fake coins either, as the chameleons can mess things us up by consistently pretending to be fake.
What we can do is to find a small number of coins some of which are guaranteed to be fake. Consider the simplest setup, when we have one fake coin and one chameleon in our mix of N coins. That is we have N − 2 real coins. Our task now is to find TWO coins, one of which has to be fake. As usual we want to do it in the smallest number of weighings that guarantees that we'll find the two coins. Let me give you a fun problem to solve:
Puzzle. The total number of coins is four. And as above we have one chameleon and one classic fake. In two weighings find two coins so that one of them is guaranteed to be fake.
If you want to learn more, we just wrote a paper titled Chameleon Coins.
* * *
—Honey, we are like two parallel lines.
—Why do you say that?
—The intersection of our life paths was a mistake.
* * *
—Q: Why did the obtuse angle go to the beach?
—A: Because it was over 90 degrees.
* * *
Ancient Roman in a clothing store: How come XL is larger than L?
* * *
—Which is the odd one out: one, three, six, seven?
—Well, three of them are odd ones.
* * *
When I am with you, I solve integrals in my head, so that blood can come back to my brain.
* * *
There are two kinds of people in this world: Those that can extrapolate from incomplete data.
* * *
Seven has the word even in it, which is odd.
I have always wanted to be an honest person and have followed my honor code. Soviet Russia had two honor codes. One code was for dealing with people and the other for dealing with businesses and the government. I remind you that in Soviet Russia, all businesses were owned by the government. The money paid for work didn't have any relation to the work done. The government paid standard salaries and the businesses did whatever. Generally, that meant that they were doing nothing. Meanwhile, the government got its income from selling oil.
All people were being screwed by the government, so they had no motivation to play fair. Just as American workers do, Soviet Russians might use the work copier to make personal copies. The difference was that we didn't feel guilty at ripping off the government. We wouldn't just make a few necessary copies; we would make copies for our friends, our family, for strangers—as many copies as possible.
I moved to the United States in 1990. Several of my friends took time to explain to me the difference between Soviet Russia and the US. One of the friends, let's call her Sarah, was working as staff at Harvard University. She told me the story of a recent visit by a famous Russian professor. After he left, the department received a bill. It appears that the professor, in a short visit, used several months-worth of the department's budget allocation for copying and phone calls. I was impressed, in a good way, by the professor who I assume spent a good deal of his time making a lot of copies of papers unavailable in Russia, presumably not only for himself but also for students and colleagues. On the other hand, it was clearly wrong.
My new friend Sarah told me that in the US money does not come from nowhere, and I should include Harvard University in my honor code for people. Actually, not only Harvard, but also any place of work and the government too. Sarah also told me that since that budget problem, she was asked to talk to every incoming Russian visitor and explain to them how capitalism works. Most Russian visitors were ready to accept the rules. I too was delighted with that. It is much easier to follow one honor code than two.
I was also very happy for my son, Alexey. He was eight when we moved to Boston. Before our move I had a dilemma. Should I tell him that Lenin and Stalin were bad guys and killed millions of people? If I gave him a truthful explanation, I would also have to teach him to lie. Otherwise, if he mentioned this at school or on the street, we would be at risk of going to prison. If I didn't teach him the truth, he might become brainwashed and grow up believing in communism, which would be very, very bad.
I was so lucky that I moved to the US: I didn't have to teach my son to lie.
Centaurs, manticores, and minotaurs roam their planet. Their society is very democratic: any two animals can become sex partners. When two different species mate, their orgasm is so potent that they merge into one creature of the third species. For example, once one centaur and one manticore make love, they are reborn as one minotaur. At the beginning of the year 2016 there were 2016 centaurs, 2017 manticores, and 2018 minotaurs. They mated non-stop and at the end of the year only one creature was left on the planet. Which one?
This is one of those puzzles that I love-hate. I hate it because it is easy to answer this puzzle by inventing a specific mating pattern that ends with one animal. It is possible to get the correct answer without seeing the beauty. I love it because there is beauty in the explanation of why, if the mating ends with one animal, it has to be a specific animal.
The solution is charming, but being a mathematician this problem makes me wonder if ii is always possible to end with one animal. So I add another puzzle.
Describe the sets of parameters for which it is impossible to end up with one creature.
Today I have two new coin puzzles that were inspired by my son, Alexey Radul:
You have N > 2 identical-looking coins. All but one of them are real and weigh the same. One coin is fake and is lighter than the real ones. You also have a balance scale which might or might not be faulty. A faulty scale differs from a normal one in reversing the sense of unbalanced weighings—it shows a lighter pan as heavier and vice versa (but still shows equal-weight pans as weighing the same). What is the smallest number of weighings you need in order to figure out whether the scale is faulty?
If you think about it, this problem is isomorphic to a known problem I wrote about before:
You have N ≥ 2 identical-looking coins. All but one of them are real and weigh the same. One coin is fake and is either lighter than the real ones or heavier than the real ones. You also have a normal balance scale. What is the smallest number of weighings you need in order to figure out whether the fake coin is lighter or heavier?
To make things more interesting let's mix the problems up.
You have N > 2 identical-looking coins. All but one of them are real and weigh the same. One coin is fake and is lighter than the real ones. You also have M > 1 identical-looking balance scales. All but one of them are normal and one is faulty. The faulty scale differs from a normal one in reversing the sense of unbalanced weighings—it shows a lighter pan as heavier and vice versa (but still shows equal-weight pans as weighing the same). What is the smallest number of total weighings needed to figure out which scale is faulty?
The following problem was at a 2016 entrance test for the MIT PRIMES STEP program.
I drew several triangles on a piece of paper. First I showed the paper to Lev and asked him how many triangles there were. Lev said 5 and he was right. Then I showed the paper to Sasha and asked him how many triangles there were. Sasha said 3 and he was right. How many triangles are there on the paper? Explain.
The intended answer was 8: there were 5 triangles on one side of the paper and 3 on the other.
Most of the students didn't think that the paper might be two-sided, but they came up with other inventive ideas. Below are some of their pictures, and I leave it to you to explain why they work. All the students who submitted these pictures got a full credit for this problem on the test.
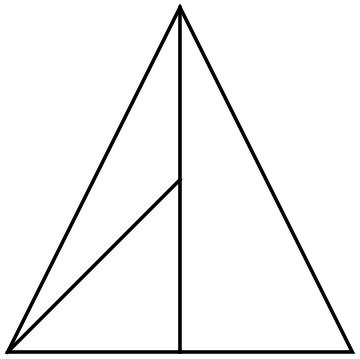



If you are a high-school student who wants to conduct research in mathematics, you should check out the MIT PRIMES program. If you enjoy solving the problems in our entrance test, that's the first indication that you might want to apply. But to determine if the program is right for you, and you are right for the program, please read the following questions and answers which have been prepared for you by Tanya Khovanova, the PRIMES Head Mentor. (This only addresses applications to PRIMES Math, and only to the research track)
Question: I do not like math competitions. Should I apply?
Answer: Math competitions are completely separate from research in mathematics. If you enjoy thinking about mathematics for long periods of time and are fascinated by our test questions, you should apply.
Question: I am good at math, but I really want to be a doctor. Should I apply?
Answer: No. PRIMES requires a huge time commitment, so math should really be your most significant interest.
Question: I want to get into Harvard, and PRIMES looks good on a resume. Should I apply?
Answer: PRIMES does look good on a resume. But if you are more passionate about, say, climate change than math, what would Harvard's admission committee see? Our experience in the program is that if math isn't your top interest, your math student may not be sufficiently impressive to be accepted at Harvard as a math researcher. At the same time, you will not be accepted as the top climate change student as you didn't invest your time in that. Math research is a hard way to earn points for college. See also, the essay, Thoughts on research by Simon Rubinstein-Salzedo.
Question: My parents want me to apply. Should I apply?
Answer: Your parents will not be accepted to the program. Do not apply if you do not really, really want to.
Question: Your website suggests that I should spend ten hours a week on the PRIMES project. I can only spend five. But I am a genius and faster than other people.
Answer: We already assume that you are a genius and faster than anyone else you know. Five hours a week are not enough for a successful project.
Question: I looked at the past PRIMES projects and nothing excites me as much as my current interest in Pascal's triangle. I doubt I should apply.
Answer: When you start working on a project, you will learn a lot about it. You will understand why, for example, Cherednik algebras are cool. The excitement comes with knowledge and invested time. Not yet being excited about Cherednik algebras is not a good reason not to apply. Besides a lot of exciting mathematics is done between several different fields.
Question: I really want to do nothing else than study Pascal's triangle.
Answer: We try to match our projects to students' interests as much as we can. But we almost never can fulfill a specific request as above. You might get a project related to Young diagrams, which are connected to quantum Pascal's triangle. If this connection doesn't excite you, you shouldn't apply.
Question: I think I will be better positioned for research if I spend five more years studying.
Answer: There is nothing wrong with this approach. For many years the standard was to start research in graduate school. Our program is innovative. At PRIMES we are trying a different model. It may sound scary, but you will learn everything you need to know in order to do your project. If the project is in representation theory, for example, you will only learn what you need—not the whole theory. Our hope is that eventually you will take a course in representation theory and expand your grasp of it and see the bigger picture behind your project. We have a reading track for people like you who reside in Boston area.
Question: I love math, but I am not sure that I want to be a mathematician. Should I apply?
Answer: Many people start loving math early in life and then discover that there are many other things that require a similar kind of brain: computer science, cryptography, finance, and so on. We do not require from our students a commitment to become mathematicians. If you want to try research in math, you should apply. If students decide that they do not want to do research in math after finishing our program, we do not consider that a negative result. One way or another, the experience of PRIMES will help you understand better what you want to do with your life.
Question: I want to get to the International Math Olympiad. I am afraid that the time the research project takes prevents me from preparing for competitions. Should I apply?
Answer: People who are good at Olympiads often have fantastic brain power that helps in research. On the other hand, research requires a different mind set and the transition might be painful. It is possible, but not trivial to succeed in both. It is up to you to decide how you want to spend your time.
Question: I like number theory, but I do not see past PRIMES projects in number theory.
Answer: Doable number theory projects are hard to come by and we have fewer number theory projects than students who want to do number theory. There are many high-school programs that teach number theory including PROMYS and Ross programs. Our applicants like number theory because they were exposed to it. During PRIMES you will be exposed to something else and might like it as much.
Question: I found a local professor to work with on a research project. Should I apply to PRIMES?
Answer: PRIMES requires that you devote 10 hours a week to research for a year. It is unrealistic to do two research projects in parallel. Choose one. Working with someone in person may be better than by Skype at PRIMES. Also, usually our mentors are not professors, but rather graduate students. On the other hand, they are MIT grad students and projects are often suggested by professors. Our program is well structured. We guarantee weekly meetings in the Spring, we give extra help with your paper, and we have a conference. It is up to you to decide.
Alexander Shapovalov is a prolific puzzle writer. He has a special webpage of his river-crossing puzzles (in Russian). Here is one of these puzzles.
Three swindlers have two suitcases each. They approach a river they wish to cross. There is one boat that can carry three objects, where a person or a suitcase counts as one object. No swindler can trust his suitcase to his swindler friends when he is away, but each swindler doesn't mind his suitcases left alone at the river shore. Can they cross the river?
In my paper with Joshua Xiong, Nim Fractals, we produced a bijection between P-positions in the three-pile Nim and a three-branch Ulam-Warburton automaton. We also defined a parent-child relationship on games that is induced by this bijection. Namely, two consecutive P-positions in a longest optimal game of Nim are the ones that correspond to a parent-child pair in the automaton. A cell in the Ulam-Warburton automaton has exactly one parent. That means, if (a,b,c) is a Nim P-position, then exactly one of (a − 1,b − 1,c), (a − 1,b,c − 1), and (a,b − 1,c − 1) must be a P-position and a parent of (a,b,c). (See our paper for more details.)
Now I want to explicitly write out the rules of an automaton which will generate the Nim P-positions in 3D.
Let me restrict the evolution of the automaton to the non-negative octant. That is, we consider points (a,b,c) in 3D, where each coordinate is a non-negative integer. We define the neighbors of the point (a,b,c) to be the points that differ from (a,b,c) in two coordinates exactly by 1. So each point strictly inside the octant has 12 neighbors. (There are three ways to choose two coordinates, and after that four ways to choose plus or minus 1 in each of them.
There is a geometric interpretation to this notion of neighborhood. Let us correspond a unit cube to a point with integer coordinates. The center of the cube is located at the given point and the sides are parallel to the axes. Then two points are neighbors if and only if the corresponding cubes share one edge. Now it becomes more visual that a cube has 12 neighbors, as it has 12 edges.
Here is the rule of the automaton. Points never die. We start with the patriarch, (0,0,0), one point being alive. The non-alive point is born inside the non-negative octant if it has exactly 1 alive neighbor that is closer to the patriarch. In other words the point (a,b,c) is born if and only if exactly one out of three points (a − 1,b − 1,c), (a − 1,b,c − 1), and (a,b − 1,c − 1) is alive. It follows that the points that are born at the n-th step has a coordinate sum 2n.
Consider for example the starting growth. At the first step the points (0,1,1), (1,0,1) and (1,1,0) are born. At the next step the points (0,2,2) and (2,0,2) and (2,2,0) are born. while the (1,1,2) will never be born as starting from the second step it has at least two live neighbors: (0,1,1) and (1,0,1) that are closer to the patriarch.
Theorem. In the resulting automaton, the points that are born at step n are exactly the P-positions of Nim with the total of 2n tokens.
Proof. Only the points with an even total can be born. Now we proceed by induction on the total number of tokens. The base case is obvious. Suppose we proved that at step n exactly P-positions with 2n tokens are born. Consider a P-position of Nim: (a,b,c) such that a + b + c = 2n + 2. Remember, that bitwise XOR of a, b, and c is zero. Consider the 2-adic values of a, b, and c (aka the smallest powers of 2 dividing a, b, and c). There should be exactly two out of these three integers that have the smallest 2-adic value. Suppose these are a and b. Then (a − 1,b − 1,c) is a P-position, while (a − 1,b,c − 1) and (a,b − 1,a − 1) are not. That means by the inductive hypothesis (a,b,c) has exactly one alive neighbor. So the position (a,b,c) is born at time n + 1.
Now we need to proof that nothing else is born. For the sake of contradiction suppose that (a,b,c) is the earliest N-position to be born. That means it has a live neighbor that is a P-position closer to the patriarch. WLOG we can assume that this neighbor is (a − 1,b − 1,c).
If a − 1 and b − 1 are both even, then (a,b,c) is a P-position, which is a contradiction. Suppose a − 1 and b − 1 are both odd. Then their binary representations can't have the same number of ones at the end. Otherwise, (a,b,c) is a P-position. That is a and b have different 2-adic values. Suppose a has a smaller 2-adic value, Then, for (a − 1,b − 1,c) to be a P-position a and c has to have the same 2-adic value. That means (a,b − 1,c − 1) is a P-position too. Now suppose a − 1 and b − 1 are of different parities. Without loss of generality suppose a − 1 is odd and b − 1 is even, then c is odd. Then (a − 1,b,c − 1) is a P-position too. Thus we can always find a second neighbor with the same number of tokens. That is, both neighbors are alive at the same time; and the N-position (a,b,c) is never born. □
One might wonder what happens if we relax the automaton rule by removing the constraint on the distance to the patriarch. Suppose a new point is born if it has exactly one neighbor alive. This will be a different automaton. Let us look at the starting growth, up to a permutation of coordinates. At step one, positions (0,1,1) are born. At the next step positions (0,2,2) are born. At the next step positions (0,1,3), (1,2,3) and (0,3,3) are born. We see that (0,1,3) is not a P-positions. What will happen later? Will this N-position mess up the future positions that are born? Actually, this automaton will still contain all the P-positions of Nim.
Theorem. In the new automaton, the points that are born at step n and have total of 2n tokens are exactly the P-positions of Nim with the total of 2n tokens.
Proof. Only the points with an even total can be born. Now we proceed by induction on the total number of tokens. The base case is obvious. The birth of the points that have total of 2n tokens and are born at step n depend only on the points with the total of 2n − 2 tokens that are born at step n − 1. By the inductive hypothesis, those are the P-positions with 2n − 2 tokens. So the points have total of 2n tokens and are born at step n match exactly the first automaton described above. To reiterate, N-positions with 2n tokens are born after P-positions with 2n tokens, so they do not influence the birth of P-positions with 2n + 2 tokens. □
In the game of Nim you have several piles with tokens. Players take turns taking several tokens from one pile. The person who takes the last token wins.
The strategy of this game is well-known. You win if after your move the bitwise XOR of all the tokens in all the piles is 0. Such positions that you want to finish your move with are called P-positions.
I play this game with my students where the initial position has four piles with 1, 3, 5, and 7 tokens each. I invite my students to start the game, and I always win as this is a P-position. Very soon my students start complaining that I go second and want to switch with me. What should I do? My idea is to make the game last long (to have many turns before ending) to increase the chances of my students making a mistake. So what is the longest game of Nim given that it starts in a P-position?
Clearly you can't play slower then taking one token at a time. The beauty of Nim is that such an optimal game starting from a P-position is always possible. I made this claim in several papers of mine, but I can't find where this is proven. One of my papers (with Joshua Xiong) contains an indirect proof by building a bijection to the Ulam-Warburton automaton. But this claim is simple enough, so I want to present a direct proof here. Actually, I will prove a stronger statement.
Theorem. In an optimal game of Nim that starts at a P-position the first player can take one token at each turn so that the second player is forced to take one token too.
Proof. Consider a P-position in a game of Nim. Then find a pile with the lowest 2-adic value. That is the pile such that the power of two in its factorization is the smallest. Suppose this power is k. Notice that there should be at least two piles with this 2-adic value.
The first player should take a token from one of those piles. Then the bitwise heap-sum after the move is 2k+1−1. Then the Nim strategy requires the second player to take tokens from a pile such that its value decreases after bitwise XORing with 2k+1−1. All piles with the 2-adic value more than k will increase after xoring with 2k+1−1. That means the second player has to take tokens from another pile with 2-adic value k. Moreover, the second player is forced to take exactly one token to match the heap-sum. □
In the position (1,3,5,7) all numbers are odd, so I can take one token from any pile for my first move, then the correct move is to take one token from any other pile. My students do not know that; and I usually win even as the first player. Plus, there are four different ways I can start as the first player. This way my students do not get to try several different options with the same move I make. After I win several times as the first player, I convince my students that I win anyway and persuade them to go back to me being the second player. After that I relax and never lose. I am evil.
Replace question marks with letters in the following sequence:
Y, Y, ?, ?, Y, ?, Y, ?, R, R, R, R.
Problem 1. It is true that it is possible to put positive numbers at the vertices of a triangle so that the sum of two numbers at the ends of each side is equal to the length of the side?
This looks like a simple linear algebra question with three variables and three equations. But it has a pretty geometrical solution. What is it?
Problem 2. Prove that it is possible to assign a number to every edge of a tetrahedron so that the sum of the three numbers on the edges of every face is equal to the area of the face.
Again we have six sides and four faces. There should be many solutions. Can you find a geometric one?
Do you know how to cut a cake? I mean, mathematically. There is a whole area of mathematics that studies cake cutting.
Mathematicians usually assume that each person has their own idea of what is the best part of the cake. Suppose three sisters are celebrating the New Year by having a cake. Anna likes only icing, Bella likes only chocolate chips, and Carol likes only pieces of walnuts mixed into the cake. Mathematicians want to cut cakes fairly. But what is fair? Fair is fair, right? Wrong. There are several different notions of fair cake division.
There is a proportionate division. In such a division every sister gets at least one-third of her value of the cake. This seems fair. Let's see an example. Anna gets one third of the icing, Bella gets one third of the chocolate chips, and Carol gets everything else. This is a fair proportionate division. Each of the sisters believes that she got at least one-third of the cake, in their own value. But it doesn't seem quite fair.
There is a stronger notion of fairness. It is called envy-free. In this division each sister gets at least one-third of the cake and, in addition, none of the three sisters would improve their value by swapping pieces. That means, if Anna wants only icing, not only does she get at least one-third of the icing, but also no one else gets more icing than Anna. The previous example of the proportionate division is not envy-free. Carol got two-thirds of the icing, so Anna would want to switch with her.
Let's try a different division. Anna gets one third of the icing, Bella gets the chocolate chips and another third of the icing, and Carol gets all the walnuts and another third of the icing. Formally, this is envy-free cake cutting. But poor Anna. What do you think Anna feels when she sees the smiles of contentment on the faces of her sisters? Whoever invented the name doesn't understand envy. Anna got one-third of the cake by her value, but the other sisters got the whole cake!
Luckily mathematicians understand this conundrum. So they invented another name for a cake division. They call a division equitable if everyone values all the pieces the same. So the division above is envy-free but not equitable. Let's try again. Let's give each sister one-third of all the components of the cake. This division is very good mathematically: it is proportionate, envy free, and equitable. By the way, envy-free division is always proportionate. This division seems fair. But is it a good division?
There is another term here: Pareto-efficient division means that it is impossible to make one person feel better, without making another person feel worse. All divisions above are not Pareto-efficient. Moving some icing from Carol to Anna, doesn't decrease the value for Carol, but increases the value for Anna.
There is an even better way to divide the cake. We can give the icing to Anna, the walnuts to Bella, and the chocolate chips to Carol. This division is proportionate, envy-free, and Pareto-efficient. It is perfect. Mathematicians even have a word for it. They call it a perfect division.
Mathematically this division is perfect. Unfortunately, sisters are not. I know an Anna who would still envy Bella.
Why are manhole covers round? The manhole covers are round because the manholes are round. Duh! But the cute mathematical answer is that the round shapes are better than many other shapes because a round cover can't fall into a round hole. If we assume that the hole is the same shape as the cover but slightly smaller, then it is true that circular covers can't fall into their holes. But there are many other shapes with this property. They are called the shapes of constant width.
Given the width, the shape with the largest area is not surprisingly a circle. The shape with the smallest area and a given constant width is a Reuleaux Triangle. Here is how to draw a Reuleaux triangle. Draw three points that are equidistant from each other at distance d. Then draw three circles of radius d with the centers at given points. The Reuleaux triangle is the intersection of these three circles.
Can we generalize this to 3d? What would be an analogue of a Reuleaux Triangle in 3d? Of course, it is a Reuleaux Tetrahedron: Take four points at the vertices of a regular tetrahedron; take a sphere at each vertex with the radius equal to the edge of the tetrahedron; intersect the four spheres.
Is this a shape of the constant width? Many people mistakenly think that this is the case. Indeed, if you squeeze the Reuleaux tetrahedron between two planes, one of which touches a vertex and another touches the opposite face of the curvy tetrahedron, then the distance between them is equal to d: the radius of the circle. This might give you the impression that this distance is always d. Not so. If you squeeze the Reuleaux tetrahedron between two planes that touch the opposite curvy edges, the distance between these planes will be slightly more than d. To create a shape of constant width you need to shave off the edges a bit.

Theoretically you can shave the same amount off every edge to get to a surface of constant width. But this is not the cool way to do it. The cool way is to shave a bit more but only from one edge of the pair of opposite edges. You can get two different figures this way: one that has three shaved edges forming a triangle, and the other, where three shaved edges share a vertex. These two bodies are called Meissner bodies and they are conjectured to be shapes of the constant width with the smallest volume.
On the picture I have two copies of a pair of Meissner bodies. The two left ones have three edges that share a vertex shaved off. The very left shape gives a top view of this vertex and the solid next to it has its bottom with holes looking forward. The two shapes on the right show the second Meissner body in two different positions.
I recently discovered a TED-Ed video about manhole covers. It falsely claims that the Reuleaux tetrahedron has constant width. I wrote to TED-Ed, to the author, and posted a comment on the discussion page. There was no reaction. They either should remove the video or have an errata page for it. Knowingly keeping a video with an error that is being viewed by thousands of people is irresponsible.
I am running a PRIMES-STEP program for middle school students, where we try to do research in mathematics. In the fall of 2015 we decided to study the following topic in logic.
Suppose there is an island where the following four types of people live:
See if you can solve this simple logic puzzle about people on this island.
It is known that exactly one person stole an expensive painting from an apartment. It is also known that only Alice or Bob could have done it. Here are their statements:
Alice: I am guilty. Bob is a truth-teller.
Bob: I am guilty. Alice stole it. Alice is the same type as me.
Who stole the painting and what types are Alice and Bob?
My students and I discovered a lot of interesting things about these four types of people and wrote a paper: Who Is Guilty?. This paper contains 11 cute logic puzzles designed by each of my 11 students.
I envied my students and decided to create two puzzles of my own. You have already solved the one above, so here is another, more difficult, puzzle:
A bank was robbed and a witness said that there was exactly one person who committed the robbery. Three suspects were apprehended. No one else could have participated in the robbery.
Alice: I am innocent. Bob committed the crime. Bob is a truth-teller.
Bob: I am innocent. Alice is guilty. Carol is a different type than me.
Carol: I am innocent. Alice is guilty.
Who robbed the bank and what types are the suspects?
The following cute puzzle of unknown origins was sent to me by Martina Balagovic and Vincent van der Noort:
A car travels from A to B and back again. When going uphill it goes 56 km an hour, when going downhill it goes 72 km an hour and while driving on flat surface it goes 63 km an hour. Getting from A to B takes 4 hours and getting back (over the same road) takes 4 hours and 40 minutes.
What is the distance between A and B?

I received a book Really Big Numbers by Richard Schwartz for review. I was supposed to write the review a long time ago, but I've been procrastinating. Usually, if I like a book, I write a review very fast. If I hate a book, I do not write a review at all. With this book I developed a love-hate relationship.
Let me start with love. I enjoyed reading the first 80 pages. The pictures are great, and some explanations are very well thought out. Plus, I haven't thought much about really big numbers, so the book helped me understand them. I was impressed with how this book treats very difficult ideas with simple explanations and illuminating images. I was captivated by it.
Now to hate. I had two problems with this book: one pedagogical and the other mathematical.
The pedagogical issue. The beginning of the book is suitable for small children. Most of the book is suitable for advanced middle-schoolers who like mathematics. The last part is very advanced. Is it a good idea to show children a book that looks like a children's book, but which soon becomes totally out of their reach? Richard Schwartz understands it and says many times that pieces of this book might be read several years apart. Several years? What child is ready to wait several years to finish a book? How would children feel about the book and about numbers when no matter how hard they try, they cannot understand the end of the book?
As a reviewer, I can't recommend the full book for kids who are not ready to grasp the notion of the Ackermann function or arrow notation. Even if the child is capable of understanding these ideas, there are mathematical issues that would prevent me from recommending it.
The mathematical issue. Let me start by explaining the notion of plex. We call an n-plex a number that is equal to 10n. For example, 2-plex means 102 which is 100, and 10-plex means 1010. The fun part starts when we plex plexes. The number n-plexplex means 10 to the power n-plex which is 10(1010). We can continue plexing: n-plexplexplex means 10 to the power n-plexplex. When you are hunting for really big numbers, it is easier to write the number of plexes rather than writing plexes after plexes. Richard Schwartz introduces the following notation to help visualize the whole thing. He puts numbers in a square. Number n in a square means 1-plexed n times. For example, 2 inside a square means 1010. Ten inside a square is 1-plexplexplexplexplexplexplexplexplexplex.
We can start nesting squares. For example, 2 inside a square means 1-plex-plex or 1010. Let's add a square around it: 2 inside two squares means 1010 inside a square, which equals 1 plexed 1010 times. To denote 10 nested in n squares Richard Schwartz uses the next symbol: n inside a pentagon. For example, 1 inside a pentagon is 10 inside a square. I wrote this number in the previous paragraph: it is 1-plexplexplexplexplexplexplexplexplexplex. Similarly, n inside a hexagon means 10 inside n nested pentagons. We can continue this forever: n inside a k-gon is 10 inside k nested (k-1)-gons.
What bothers me is why a square? Why not a triangle? If we adopt this scheme, what is the meaning of a number in a triangle? Let's try to unravel this. Following Richard Schwartz's notation we get that n inside a square is the same as 10 inside n nested triangles. What do we do n times with 10 to get to 1 plexed n times? 1-plexed n times is 10 plexed n-1 times. There is a disconnect in notation here. For example, 10 in two nested triangles should mean 2 inside a square that is 1010. 10 inside one triangle should mean 1 inside a square which is 10. This doesn't make any sense.
I started googling around and discovered the Steinhaus–Moser notation. In this notation a number n in a triangle means nn. A number n in a square means the number n inside n nested triangles. A number n in a pentagon means the number n inside n nested squares. And so on. This makes total sense to me. If we move down the number of sides, we can say that the number n inside a 2-gon means n times n and the number n inside a 1-gon means n. This is perfect.
Schwartz changed the existing notation in two places. First he made everything about 10. This might not be such a bad idea except his 10 inside a square doesn't equal 10 inside a square in Steinhaus–Moser notation. In Steinhaus–Moser notation 10 inside a square means 10 plexed 10 times. The author removed one of the plexes. He made 10 inside the square to mean 1 plexed 10 times, and as a result it stopped working.
Even though the first 83 pages are delightful and the pictures are terrific, the notation doesn't work. What a pity.
I have solved too many puzzles in my life. When I see a new one, my solution is always the intended one. But my students invent other ideas from time to time and teach me to think creatively. For example, I gave them this puzzle:
Two boys wish to cross a river, but there is a single boat that can take only one boy at a time. The boat cannot return on its own; there are no ropes or similar tricks; yet both boys manage to cross the river. How?
Here is what my inventive students came up with:
And here is my standard solution: They started on different sides of the river.
I gave a talk about thinking inside and outside the box at the Gathering for Gardner conference. I mentioned this puzzle and the inventiveness of my students. After the conference a guy approached me with another answer which is now my favorite:
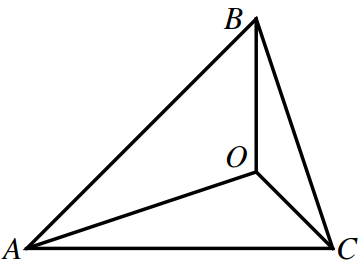
Consider a triangle with vertices A, B, and C. Let O be its orthocenter. Let's connect O to the vertices. We get six lines: three sides of the triangle and three altitudes. These six lines are pair-wise orthogonal: AO ⊥ BC, BO ⊥ AC, and CO ⊥ AB.
It is easy to see that A is the orthocenter of the triangle OBC, and so on: each vertex is the orthocenter of the triangle formed by the other three. We say that these four points form an orthocentric system.
I heard a talk about this structure at the MOVES 2015 conference by Richard Guy. What I loved in his talk was his call to equality and against discrimination. The point O plays the same role as the other three points. It should be counted. Richard Guy suggested calling this system an orthogonal quadrangle. I am all for equality. This is not a triangle, this is a quadrangle!
I want the world to be a better place. My contribution is teaching people to think. People who think make better decisions, whether they want to buy a house or vote for a president.
When I started my blog, I posted a lot of puzzles. I was passionate about not posting solutions. I do want people to think, not just consume puzzles. Regrettably, I feel a great push to post solutions. My readers ask about the answers, because they are accustomed to the other websites providing them.
I remember I once bought a metal brainteaser that needed untangling. The solution wasn't included. Instead, there was a postcard that I needed to sign and send to get a solution. The text that needed my signature was, "I am an idiot. I can't solve this puzzle." I struggled with the puzzle for a while, but there was no way I would have signed such a postcard, so I solved it. In a long run I am glad that the brainteaser didn't provide a solution.
That was a long time ago. Now I can just go on YouTube, where people post solutions to all possible puzzles.
I am not the only one who tries to encourage people to solve puzzles for themselves. Many Internet puzzle pages do not have solutions on the same page as the puzzle. They have a link to a solution. Although it is easy to access the solution, this separation between the puzzle and its solution is an encouragement to think first.
But the times are changing. My biggest newest disappointment is TED-Ed. They have videos with all my favorite puzzles, where you do not need to click to get to the solution. You need to click to STOP the solution from being fed to you. Their video Can you solve the prisoner hat riddle? uses my favorite hat puzzle. (To my knowledge, this puzzle first appeared at the 23-rd All-Russian Mathematical Olympiad in 1997.) Here is the standard version that I like:
A sultan decides to give 100 of his sages a test. He has the sages stand in line, one behind the other, so that the last person in line can see everyone else. The sultan puts either a black or a white hat on each sage. The sages can only see the colors of the hats on all the people in front of them. Then, in any order they want, each sage guesses the color of the hat on his own head. Each hears all previously made guesses, but other than that, the sages cannot speak. Each person who guesses the color wrong will have his head chopped off. The ones who guess correctly go free. The rules of the test are given to them one day before the test, at which point they have a chance to agree on a strategy that will minimize the number of people who die during this test. What should that strategy be?
The video is beautifully done, but sadly the puzzle is dumbed down in two ways. First, they explicitly say that it is possible for all but one person to guess the color and second, that people should start talking from the back of the line. I remember in the past I would give this puzzle to my students and they would initially estimate that half of the people would die. Their eyes would light up when they realized that it's possible to save way more than half the people. They have another aha! moment when they discover that the sages should start talking from the back to the front. This way each person sees or hears everyone else before announcing their own color. Finally, my students would think about parity, and voilà, they would solve the puzzle.
In the simplified adapted video, there are no longer any discoveries. There is no joy. People consume the solution, without realizing why this puzzle is beautiful and counterintuitive.
Nowadays, I come to class and give a puzzle, but everyone has already heard the puzzle with its solution. How can I train my students to think?
I stumbled upon a TED-Ed video with a frog puzzle:
You're stranded in a rainforest, and you've eaten a poisonous mushroom. To save your life, you need an antidote excreted by a certain species of frog. Unfortunately, only the female of the species produces the antidote. The male and female frogs occur in equal numbers and look identical. There is no way to distinguish between them except that the male has a distinctive croak. To your left you spot a frog on a tree stump. You hear a croak from a clearing in the opposite direction, where you see two frogs. You can't tell which one made the sound. You feel yourself starting to lose consciousness, and you realize that you only have time to run in one direction. Which way should you go: to the clearing and lick both frogs or to the tree stump and lick the stump frog?
My first thought was that male frogs croak to attract female frogs. That means the second frog in the clearing is probably an already-attracted female. The fact that the stump frog is not moving means it is male. I was wrong. This puzzle didn't assume any knowledge of biology. The puzzle assumes that each frog's gender is independent from other frogs. Thus this puzzle is similar to two-children puzzles that I wrote so much about. I not only blogged about this, but also wrote a paper: Martin Gardner's Mistake.
As in two-children puzzles, the solution depends on why the frog croaked. It is easy to make a reasonable model here. Suppose the male frog croaks with probability p. Now the puzzle can be solved.
Consider the stump frog before the croaking:
Consider the two frogs in the clearing before the croaking:
The probabilities corresponding to our outcome—a non-croaking frog on the stump and one croaking frog in the clearing—are in bold. Given that the stump frog is silent, the probability that it's a female is 1/(1-p). Given that one clearing frog croaked, the probability that one of them is a female is p/2 divided by p(1-p)/2. The ratio is the same 1/(1-p). It doesn't matter where you go for the antidote.
The TED-Ed's puzzle makes the same mistake that is common in the two-children puzzles. I don't want to repeat their incorrect solution. The TED-Ed's frog puzzle is wrong.
When I receive a bank statement, I review all the transactions. The problem is my failing memory. I do not remember when and where I last took money from an ATM, and how much. So I decided to create a pattern. I used to take cash in multiples of 100. Probably most people do that. A better idea is to always take the amount that has a fixed remainder modulo 100, but not 0. For example, let's say I take one of the following amounts: 40, 140, 240, or 340. Sometimes I need more money, sometimes less. This set of numbers covers all of my potential situations, but my pattern is that all the numbers end in 40. This way if someone else gets access to my account, they will almost surely take a multiple of 100. I will be able to discover a fraud without remembering the details of my last withdrawal.
In addition, when I first started doing this, I was hoping I wouldn't need to wait until I review my own statement to discover problems. My hope was that if a thief tried to take cash from my account, my bank would notice a change in the pattern and notify me immediately. Now I realize that this was wishful thinking. I doubt that banks are as smart as I am.
One day I should try an experiment. I should go to an ATM I never use and withdraw 200 dollars. I wonder if my bank would notice.
One of my jobs is giving linear algebra recitations at MIT. The most unpleasant aspect of it is dealing with late homework. Students attempt to submit their homework late for lots of different reasons: a sick parent needing help, stress, a performance at Carnegie Hall, a broken printer, flu, and so on. How do I decide which excuse is sufficient, and which is not? I do not want to be a judge! Moreover, my assumption is that people tell the truth. In the case of linear algebra homework, this assumption is unwise. As soon as students discover that I trust everyone, there's a sharp increase in the number of sick parents and broken printers. So I have the choice of being either a naive idiot or a suspicious cynic. I do not like either role.
Our linear algebra course often adopts a brilliant approach: We announce that late homework is not allowed for any reason. To compensate for emergencies, we drop everyone's lowest score. That is, we allow the students to skip one homework out of ten. They are free to use this option for oversleeping the 4 pm deadline. If all their printers work properly and they do not get so sick that they have to skip their homework, they can forgo the last homework. Happily, this relieves me from being a judge.
Or does it? Unfortunately, this policy doesn't completely resolve the problem. Some students continue trying to push their late homework on me, despite the rules. In order to be fair to other students and to follow the rules, I reject all late homework. The students who badger me nonetheless waste my time and drain my emotions. This is very unpleasant.
From the point of view of those students, such behavior makes sense. They have nothing to lose and they might get some points. There is no way to punish a person who tries to hand in homework late and from time to time they stumble onto a soft instructor who accepts the homework against the official rules. Because such behavior is occasionally rewarded, they continue doing it. I believe that wrong behavior shouldn't be rewarded. As a responsible adult, I think it is my duty to counteract the rewards of this behavior. But I do not know how.
What should I do? Maybe I should…
Maybe I should just do number 4 right now and explain what I feel. A student who persists in handing in homework late feels to me that s/he is entitled and is better than everyone else, and shows that s/he doesn't care about the rules and honor. Again, this wastes my time, puts me in a disagreeable position, and reduces my respect for that student.
Earlier I suggested that students don't have anything to lose by such behavior, but in fact, they do pay a price, even though they may not understand that.
I found the following puzzle on a facebook page of Konstantin Knop (in Russian):
Seven astronauts landed on a small spherical asteroid. They wanted to explore it and walked in different directions starting from the same location. All used the same walking algorithm: walk x kilometers forward, turn 90 degrees left and walk another x kilometers, turn 90 degree left again and walk the last x kilometers. The value of x was different for different astronauts and was one of 30, 40, 50, 60, 70, 80, and 90.
All but one astronaut finished in the same location. What was the value of x for the astronaut who finished alone? What is the size of the asteroid?
I've been collecting math jokes for many years. I thought I've seen them all. No. Inventive people continue to create them. I was recently sent a link to a math joke website that features many jokes that are new to me. Here are my favorites:
* * *
With massive loss of generality, let $n=5$.
* * *
How do you prove a cotheorem? Using rollaries.
* * *
$0\to A\to B \to C \to 0$. Exactly.
* * *
Let $\varepsilon\to 0$. There goes the neighborhood!
* * *
Take a positive integer $N$. No, wait, $N$ is too big; take a positive integer $k$.
* * *
Calculus has its limits.
* * *
There is a fine line between a numerator and a denominator.
* * *
There's a marked difference between a ruler and a straightedge.
* * *
Suppose there is no empty set. Then consider the set of all empty sets.
* * *
Q: Why is it an insult to call someone "abelian"?
A: It means they only have a 1-dimensional character, and are self-centered.
* * *
Q: What's a polar bear?
A: A rectangular bear after a coordinate transform.
* * *
A logician rides an elevator. The door opens and someone asks:
—"Are you going up or down?"
—"Yes."

Russians cherish the issues of Kvant, a famous Soviet monthly magazine for high-school students devoted to math and physics. At its peak its circulation was about 300,000, which is unparalleled for a children's science journal. I still have my old childhood issues somewhere in my basement. But one issue is very special: it has a prominent place in my office. I didn't receive it by subscription; I received it as a gift from my brother Misha.
Strictly speaking Misha is not my brother, but rather a half-brother. His full name is Mikhail Khovanov and he is a math professor at Columbia. The signed issue he gave me contains his math problem published in the journal. He invented this problem when he was a 10th grader. Here it is:
In a convex n-gon (n > 4), no three diagonals are concurrent (intersect at the same point). What is the maximum number of the diagonals that can be drawn inside this polygon so that all the parts they divide into are triangles?
He designed other problems while he was in high school. All of them are geometrical in nature. The journal is available online, and a separate document with all the math problems is also available (in Russian). His problems are M1038, M1103, M1108 (above), M1119, M1153, M1204. I like his other problems too. M1153 (below) is the shortest problem on his list: as usual I am guided by my laziness.
What's the greatest number of turns that a rook's Hamiltonian cycle through every cell on an 8 by 8 chessboard can contain?
I wanted to accompany this post with a picture of my brother at the age he was when he invented these problems—about 16. Unfortunately, I don't have a quality picture from that period. I do have a picture that is slightly off: by about ten years.
What are the Ford circles? A picture is worth a thousand words, so here is a picture.

We draw a circle for any rational number p/q between 0 and 1 inclusive. We assume that p/q is the representation of the number in the lowest terms. Then the center of the circle is located at (p/q,1/q) and the radius is 1/q. The number inside a circle is q.
Here's the game. We start with any circle on the picture, except for the two largest circles corresponding to integers 0 and 1. In one move we can switch to a larger circle that touches our circle. The person who ends up at the two largest circles corresponding to integers 0 or 1 loses. Equivalently, the person who ends in the central circle marked "2" wins.
There are other ways to describe moves in this game in terms of rational numbers corresponding to circles, that is, the x-coordinates of their centers. Two circles corresponding to numbers p/q and r/s touch each other iff one of the following equivalent statements is true:
Let me explain the last bullet. Given two rational numbers in their lowest terms a/b and c/d, we generate their mediant as: (a+c)/(b+d). We call the two numbers a/b and c/d the parents of the mediant (a+c)/(b+d). The Stern-Brocot tree starts with two parents 0/1 and 1/1. Then their mediant is inserted between them to create a row: 0/1, 1/2, and 1/1. Then all possible mediants of two consecutive numbers are inserted in a given row to get a new row. The process repeats ad infinitum. The famous theorem states that any rational number between 0 and 1 will appear in the process.
What I like about this game is a simple and beautiful description of P-positions (These are the positions you want to end your move at in order to win.) P-positions are numbers with even denominators in their lowest terms.

In the picture above P-positions are blue, while other positions are red. All circles touched by blue are red. And if we look at the larger neighbors of every red circle, one of them is blue and one is red.
Let's prove that the numbers with even denominators satisfy the conditions for P-positions. First, two circles corresponding to numbers with even denominators can't touch each other. Indeed, the cross-determinant of two such fractions is divisible by 2. Second, each red circle has to touch one blue and one red circle with larger radii. Indeed, the circles with larger radii touching a given circle are exactly the parents of the circle. If the mediant has an odd denominator, then one of the parents must have an even denominator and the other an odd denominator.
Let us start with regular (non-weighted) mediants. Suppose we have two fractions a/b and c/d, the mediant of these two numbers is the wrong way a child might sum these two fractions: (a+c)/(b+d). There is nothing wrong with this childish way of summing, it is just not a sum of two numbers, but rather an operation the result of which is called a mediant. One must be careful: the result doesn't depend on the initial numbers chosen, but on their representations. The way to deal with this is to assume that a/b, c/d, and (a+c)/(b+d) are in their lowest terms.
The numerical value of the mediant is always in between given numbers. This is probably why it is called a mediant.
Suppose you start with two rational numbers 0/1 and 1/1, and insert a mediant between them. If you continue doing it recursively, you can reach any rational number between 0 and 1. This is a well-known property of the mediants. For example, after three rounds of inserting mediants into the initial sequence (0/1, 1/1), we get the sequence: 0/1, 1/4, 1/3, 2/5, 1/2, 3/5, 2/3, 3/4, 1/1.
The mediants are easy to generalize if we assign weights to initial fractions. Suppose the first fraction has weight m and the second n, then their weighted mediant is (am+cn)/(bm+dn). The simplest generalization happens when the total weight, m+n is 3. In this case, given two rational numbers a/b and c/d, the left mediant is (2a+c)/(2b+d) and the right one is (a+2c)/(b+2d). Obviously the inequality property still holds. If a/b ≤ c/d, then a/b ≤ (2a+c)/(2b+d) ≤ (a+2c)/(b+2d) ≤ c/d.
James Propp suggested the following question for our PRIMES project. Suppose the starting numbers are 0/1 and 1/1. If we recursively insert two weighted mediants in order between two numbers we will get a lot of numbers. For example, after two rounds of inserting weighted mediants into the initial sequence (0/1, 1/1), we get the sequence: 0/1, 1/5, 2/7, 1/3, 4/9, 5/9, 2/3, 5/7, 4/5, 1/1. It is easy to see that new fractions must have an odd denominator. Thus unlike the standard case, not every fraction will appear. The question is: will every rational number between 0 and 1, which in reduced form has an odd denominator appear?
I started working on this project with Dhroova Aiylam when he was a high-school junior. We didn't finish this project during the PRIMES program. But Dhroova finished another project I already wrote about: he analyzed the case of the standard mediants with any starting points. He showed that any rational number in between the starting points appears.
Dhroova became an undergraduate student at MIT and we decided to come back to the initial PRIMES project of weighted mediants. In our paper Stern-Brocot Trees from Weighted Mediants we prove that indeed every fraction with an odd denominator between 0 and 1 appears during the recursive procedure. We also analyzed what happens if we start with any two rational numbers.

My brother, Mikhail Khovanov, has invented a new game: Ringiana. It is now available for iPhone, and soon should be available for Android.
In the starting position you see four multi-colored quadrants of a ring. For example, the first picture shows the starting position of level 33.
You can either swipe or touch between the quadrants. A swipe expands one quadrant into two quadrants and compresses two other quadrants into one. You can swipe clockwise or counterclockwise. The second figure shows the result of the clockwise swipe of the North opening. The NW quadrant that was half-red and half-yellow has expanded into two quadrants. The red piece now occupies the entire NW quadrant and the yellow piece—the entire NE quadrant. Two East quadrants got contracted into one SE quadrant. The former blue NE quadrant became the top blue half of the SE quadrant. The former SE half-blue half-green quadrant became the bottom half of the SE quadrant. In general the quadrant where the swiping movement starts expands in the direction of the swipe and the quadrant where the swiping movements ends together with the next quadrant compresses.

You can also touch an opening between quadrants. In this case the neighboring quadrants exchange places. The third figure shows the result of touching the East opening.
The goal of the game is to reach the final position: have each quadrant in one color. The next image shows the end of this particular level. As you can see the game was finished in 7 moves. In this particular case this is the smallest number of moves possible. To tell you a secret, it wasn't me who finished the game in the smallest number of moves: it was my brother.

There is also a tutorial for this game on youtube.
I was at the 1976 International Mathematics Olympiad as part of the USSR team. There were eight people on the team and I decided to find out what they have achieved in the last 40 years. Here is the picture of our team. From left to right: Sergey Finashin, Yuri Burov, Nikita Netsvetaev, Boris Solomyak, Alexander Goncharov, Tanya Khovanova, Sergei Mironov, our chaperone Z.I. Moiseeva, our team leader A.P. Savin, no clue who this is (probably a translator), Piotr Grinevich.

The list below is ordered by the number of points received at the Olympiad.
Tanya Khovanova, 39 points: a lecturer at MIT. I am interested in a wide range of topics, mostly recreational mathematics and have written 60 papers.
Sergey Finashin, 37 points: a full professor at Middle East Technical University in Turkey, who is interested in topology. He wrote 40+ papers.
Alexander Goncharov, 37 points: a full professor at Yale University. He is the highest achiever on the team. He won the EMS Prize in 1992 and was an Invited Speaker at the 1994 International Congress of Mathematicians. He is interested in geometry, representation theory, and mathematical physics. He published 75 papers in refereed journals.
Nikita Netsvetaev, 34 points: a full professor at Saint-Petersburg University in Russia. He is interested in topology and algebraic geometry and wrote 20 papers.
Boris Solomyak, 31 points: a full professor at Bar-Ilan University. He is interested in fractal geometry and dynamical systems and wrote 90 papers.
Piotr Grinevich, 26 points: a leading scientific researcher at the Landau Institute for Theoretical Physics. He also teaches at Moscow State University. He is interested in integrable systems and wrote 80 papers.
Sergei Mironov, 24 points. Sergey became very ill while he was an undergrad. He stopped doing mathematics.
Yuri Burov, 22 points. Yuri wrote two papers, but quit mathematics after graduate school. He died several years ago from multiple sclerosis.
Six out of eight people on our team became mathematicians. Or more precisely five an a half. I consider myself a mathematician and am grateful for my position at MIT, where I run innovative programs for young mathematicians. But in the research world, a lecturer is a nobody. This makes me sad. I had to take breaks from research in order to raise my two children. And then I had to work in the private sector in order to support them. I was the best on my team and now I am the only one who is not a full professor. If you are looking for an example of how gender affects a career in academia, this is it.
For many years I tried to lose weight using the idea that most appealed to me: intuitive eating. By that I mean that you eat only when you are hungry. Looking back at frustrating years of trying, I wonder what took me so long to realize that this doesn't work.
I am most hungry at the end of a meal. The only time I want to kill people is when they get between me and my future third helping of cheesecake. I never get the same ravenous feeling if I haven't eaten for some time, or have just started eating.
I am least hungry in the morning. I can work on my computer for hours before I even remember that I need to eat.
When my stomach signals that it needs more food, it is always wrong. Recently, I discovered what is right. I am using myfitnesspal app for my phone that counts my calories. From time to time I know that I haven't eaten enough. At these times, I don't experience my hunger in my gut. I feel it in my head: I feel dizzy.
I decided to drop the idea of intuitive eating and outsource the decision of when and what to eat to a higher power: my smart-phone.

After graduating from MIT, my son Sergei joined Two Sigma, a hedge-fund. Last year he came to MIT representing Two Sigma at a career fair. I visited him in his booth. He was just standing there next to himself on the poster.
I should stop worrying about him. If math does not work out, he has a chance at modelling.
I have written ad nauseam about the ambiguity of problems with children. Usually a problem with two children is formulated as follows:
Mr. Smith has two children and at least one of them is a boy. What is the probability that he has two boys?
I don't want to repeat my arguments for why this problem is ambiguous. Today I want to discuss other problematic assumptions about these problems.
Assumption 1: The probability of a child being a boy is 1/2. We know that this is not the case. Usually boys are born more often than girls. In addition to that, when policy interferes, the numbers can change. When China had their one-child policy, 118 boys were born per 100 girls. That makes a probability of a boy 0.54.
Assumption 2: The gender of one child in a family is independent of the gender of the other children. I am not sure where this assumption comes from, but I easily came up with a list of possible influences on this situation.
I would like to discuss how the last bullet point changes the probabilities in two children problems. Let us consider China. Up to now China had a one-child policy with some exceptions. In some cases if the first child was a girl, the family was allowed a second child. For the sake of argument, imagine a county where people are allowed to have a second child only if the first one is a girl. A family with two boys wouldn't exist in this county. Thus the probability of having two boys is zero.
I tried to find the data about the distribution of children by gender in multi-children families. I couldn't find any. I would be curious to know what happens in real life, especially in China.
A long time ago, before anyone ever heard about ultrasound, there was a psychic who could predict the gender of a future child. No one ever filed a complaint against him.
The psychic had a journal in which he wrote the client's name and the gender of the future child. The beauty of the scam was that what he wrote in the journal was the opposite gender that he had predicted. Whenever a client complained that the gender was wrong, he would show the journal and argue that the client had misunderstood.
Happy clients don't return to complain.
Oh, the power of conditional probability! It is useful to understand it to run scams or to expose them.
Last revised November 2021