
This blog has a modern version at http://blog.tanyakhovanova.com/, where you can leave comments. This page contains the copies of 65 blog entries for 2019, 2020, and 2021. The latest essays are at http://www.tanyakhovanova.com/MathBlog.html
2022 is abundant, composite, even, evil, square-free, and untouchable.
In addition, 2022 is the smallest number n such that n, n+1, n+2, and n+3 have the maximal exponents in prime factorization equal 1, 2, 3, and 4 correspondingly. Indeed, 2022 = 2·3·337, 2023 = 7·172, 2024 = 23·11·23, and 2025 = 34·52.
Problem. The numbers 22021 and 52021 are expanded, and their digits are written out consecutively on one page. How many total digits are on the page?
Drabble cartoon, Jun 15 1987, by Kevin Fagan.

Problem. For how many prime numbers p, the expression 2p + p2 is a prime?
* * *
My daughter was talking at her kindergarten about what her parents do for work. She said that her mom catches bugs, invokes demons, and talks to clods.
* * *
I have neither Twitter nor Instagram. I just go for a walk to tell strangers what I ate and drank and how things are at work and at home. I have three followers: a doctor and two policemen.
* * *
Life is like Rubik's cube: fix one side, better not look at the rest.
* * *
My Roomba just devoured a piece of cheese I wanted to pick up and eat. The war between humans and robots is already here.
My friend, John Conway, had a trick to help him with tricky situations. Whenever he needed to make a non-trivial decision, he would ask himself, "What would John Conway do?" As he explained to me, he had in mind the public image he himself created. He liked the image and thought this mental trick helped him be a better, more productive, and not-to-forget, flashier person.
From time to time, I catch myself in need of a decision and ask myself, "What would John Conway do?" And he gave me the answer: I should change the question and ask myself, "What would Tanya Khovanova do?"
Here are some snowball sentences suggested by my students.
Can you invent some other snowball sentences? But first, you need to figure out what they are.
Each year I look at the MIT Mystery hunt puzzles and pick ones related to mathematics, logic, and computer science. I usually give additional comments about the puzzles, but this year's titles are quite descriptive. Let's start with mathematics.
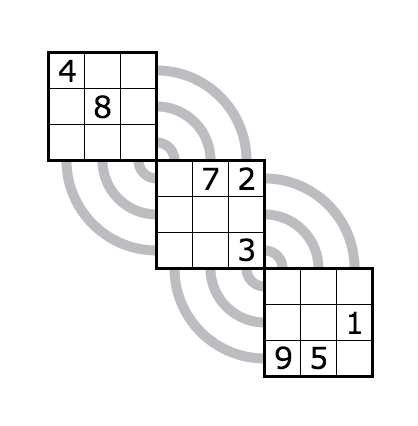
Now Nikoli-type logic puzzles. I really enjoyed "Fun with Sudoku" during the hunt.
And computer science.
I recently wrote a post, A Splashy Math Problem, with an interesting problem from the 2021 Moscow Math Olympiad.
Problem (by Dmitry Krekov). Does there exist a number A so that for any natural number n, there exists a square of a natural number that differs from the ceiling of An by 2?
The problem is very difficult, but the solution is not long. It starts with a trick. Suppose A = t2, then An + 1/An = t2n + 1/t2n = (tn + 1/tn)2 − 2. If t < 1, then the ceiling of An differs by 2 from a square as long as tn + 1/tn is an integer. A trivial induction shows that it is enough for t + 1/t to be an integer. What is left to do is to pick a suitable quadratic equation with the first and the last term equal to 1, say x2 - 6x + 1, and declare t to be its largest root.
Today I present three problems from the 41-st Tournament of the Towns that I liked: an easy one, one that reminds me of the Collatz conjecture, and a hard one.
Problem 1 (by Aleksey Voropayev). A magician places all the cards from the standard 52-card deck face up in a row. He promises that the card left at the end will be the ace of clubs. At any moment, an audience member tells a number n that doesn't exceed the number of cards left in the row. The magician counts the nth card from the left or right and removes it. Where does the magician need to put the ace of clubs to guarantee the success of his trick?
Problem 2 (by Vladislav Novikov). Number x on the blackboard can be replaced by either 3x + 1 or ⌊x/2⌋. Prove that you can use these operations to get to any natural number when starting with 1.
Problem 3 (by A. Gribalko). There are 2n consecutive integers written on a blackboard. In one move, you can split all the numbers into pairs and replace every pair a, b with two numbers: a + b and a − b. (The numbers can be subtracted in any order, and all pairs have to be replaced simultaneously.) Prove that no 2n consecutive integers will ever appear on the board after the first move.
Here is a cute old problem that Facebook recently reminded me of.
Puzzle. By mistake, a clock-maker made the hour hand and the minute hand on a clock exactly the same. How many times a day, you can't tell the current time by looking at the clock? (It is implied that the hands move continuously, and you can pinpoint their exact location. Also, you are not allowed to watch how the hands move.)
Here is the solution by my son who was working on it together with my grandson.
The right way to think about it is to imagine a "shadow minute hand", like this: Start at noon. As the true hour hand advances, the minute hand advances 12 times faster. If the true minute hand were the hour hand, there would have to be a minute hand somewhere; call that position the shadow minute hand. The shadow minute hand advances 12 times faster than the true minute hand. The situations that are potentially ambiguous are the ones where the shadow minute hand coincides with the hour hand. Since the former makes 144 circuits while the latter makes 1, they coincide 143 times. However, of those, 11 are positions where the true minute hand is also in the same place, so you can still tell the time after all. So there are 132 times where the time is ambiguous during the 12-hour period, which leads to the answer: 268.
I love the problem and gave it to my students; but, accidentally, I used CAN instead of CAN'T:
Puzzle. By mistake, a clock-maker made the hour hand and the minute hand on a clock exactly the same. How many times a day can you tell the current time by looking at the clock?
Obviously, the answer is infinitely many times. However, almost all of the students submitted the same wrong finite answer. Can you guess what it was? And can you explain to me why?
Puzzle. What is the probability of getting five Mondays in a 31-days month?
This is easy if we assume that the day of the week for the first day of the month is chosen at random. But we should know better. What is the actual probability? Bonus question: for which day of the week the probability of having this day five times in a 31-days month is the highest?
A cute puzzle found on Facebook:
Puzzle. Four wizards A, B, C, and D, were given three cards each. They were told that the cards had numbers from 1 to 12 written without repeats. The wizards only knew their own three numbers and had the following exchange.
- A: “I have number 8 on one of my cards.”
- B: “All my numbers are prime.”
- C: “All my numbers are composite. Moreover, they all have a common prime factor.”
- D: “Then I know the cards of each of you.”
Given that every wizard told the truth, what cards does A have?
* * *
I surveyed many people who had played Russian roulette. Seems like the probability of dying is actually 0%.
* * *
What has the probability of one in five million?
Zero: there's no 1 in 5000000. Only a five and six zeros.
* * *
Two classmates:
—What did you think of our probability exam yesterday?
—All means to an end.
* * *
My classmate didn't study for our test in probability.
"I'll take my chances", he said.
* * *
I saw my math teacher with a piece of graph paper yesterday. I think he must be plotting something.
* * *
Not all math puns are terrible. Just sum.
* * * (submitted by Sergei Bernstein)
A programmer walks into a bar, holds up two fingers, and says, "I'll have three beers please."
* * *
What is the similarity between me and an experiment involving a biased coin with two tails?
The probability of getting a head is zero.

I've been crocheting hyperbolic surfaces of constant curvature. The process is time-consuming, so while I am crocheting, I wonder about the mathematics of crocheting.
Hilbert's theorem says that I can't embed a hyperbolic plane in 3-dimensional space. The proof is rather involved. But here, I have an explanation from the point of view of a crochet hook. My hook starts with a tiny cycle of four stitches. Then for every x stitches the hook makes y stitches in the next row, where y is greater than x. The extra stitches should be evenly distributed to guarantee that locally every small area is approximately isomorphic to other areas, meaning that the surface has a constant curvature.
The ratio of stitches in the next row to the current row is r = y/x. Thus, the number of stitches in each row increases exponentially. But each row is a fixed height h. That means after k rows, my thingy has to fit inside a ball of radius kh. But the length of the last row is 4rk-1. It becomes huge very fast. As the last row is a physical curve made out of stitches, there is a limit of how much of it I can fit into a given volume, creating a contradiction.
That means, if I start crocheting, something should happen that won't allow me to continue. I decided to experiment and see what actually would happen. Being lazy, I preferred the disaster to happen sooner rather than later. So I chose the ratio of three: for each stitch on my perimeter, I added three new stitches. Shortly after I started to work, the process became more and more difficult. The ball was too tight. It was challenging to hold that thing in the place where I needed to insert the hook. And the loops were getting tighter, making it more exhausting to insert the hook into the proper hole. So each new stitch was taking more and more time to complete.
To my disappointment, the thing didn't explode, as I was secretly hoping: I just couldn't work on it anymore.
I like rewarding my students. Before covid, I used to give them star stickers for good ideas. When I started to teach remotely, I wondered what I should do instead. I could tell them that they had won a star, but it felt too weak. The next idea was to show them a star and tell them that it belonged to them. But that still felt insufficient. Then I had an epiphany. I would say to them they earned a star, show it to them, and stick it to my face. So they, and all the other students, would see it for the rest of the class. The photo shows how I looked at the end of a successful lesson.

Another picture shows what my MathRoots students posted on our Discord channel.
Now that I am back teaching in person, my students asked me to continue sticking their stars to my face. Sometimes I forget about the stars and, after my class, wander around MIT star-covered.
My son, Alexey Radul, wrote a program that finds the largest numbers to start a sequence in the Online Encyclopedia of Integer Sequences (OEIS). To my surprise, the top ten are all numbers consisting of ones only. The largest number is 11111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111: a number with 128 ones. The sequence is A095646: a(n) is 128 written in base n. It starts with base 1, or more precisely, the unary expansion, which indeed requires 128 ones to express the number 128.
I decided to expand my top list to 50. Again, most of the numbers are bunches of ones: 48 out of the top 50 numbers are unary expansions of numbers 81 through 128. There are two more numbers in the top 50 that are different and belong to awesome sequences.
The first sequence is sequence A033290: Ten consecutive primes in arithmetic progression. It starts with the number 100996972469714247637786655587969840329509324689190041803603417758904341703348882159067229719, which has 93 digits. This number takes 37th place on my list.
The second sequence is sequence A291042: One powerful arithmetic progression with a nontrivial difference and maximal length. The sequence corresponds to a cool puzzle that appeared in the American Mathematical Monthly in 2000. The question was, "What is the length of the longest non-constant arithmetic progression of integers with the property that the kth term is a perfect kth power?" The answer is 5. John P. Robertson proved that such progression can't have 6 terms and provided an example of a sequence with 5 terms, which is the sequence in the OEIS.
Here is how to construct this sequence. Start with an arithmetic progression 1, 9, 17, 25, 33, and multiply each term by 32453011241720: the result is also an arithmetic progression. The first term is trivially a first power. The second term is 32653011241720 = (31351511121710)2 and a square. The third term is 32453011241721 = (38510118177)3 and a cube. The fourth term is 32453211241720 = (3658116175)3 and a fourth power. The fifth term is 32553011251720 = (3556115174)5 and a fifth power.
The sequence starts with the number 10529630094750052867957659797284314695762718513641400204044879414141178131103515625. It has 83 digits, and it takes 48th place on my list.
My students (Matvey Borodin, Eric Chen, Aidan Duncan, Boyan Litchev, Jiahe Liu, Veronika Moroz, Matthew Qian, Rohith Raghavan, Garima Rastogi, Michael Voigt) and I recently wrote a paper connecting the stable marriage problem and Sudoku. I just blogged about it. By the way, my students are in grades 7-9.
On the way, we invented a new type of Sudoku, which we call joint-groups Sudoku. This type is in contrast to a famous type of Sudoku, called disjoint-groups Sudoku. In a disjoint-groups Sudoku, in a particular place in a 3 by 3 box, all the digits are distinct across all the boxes. For example, the top-left corners of nine boxes have all the digits 1 thought 9. This creates nine additional disconnected regions (depending on the placements inside a 3 by 3 box) to add to columns, rows, and boxes that have to contain distinct digits.
For our new type, we wanted the digits in a particular place in each box, instead of being different, to be the same as much as possible. How much of sameness is possible? The first row contains three top-left corners. Thus, by Sudoku rules, these top-left corners have to be distinct. Thus, the top-left corners in all nine boxes have to contain at least three distinct digits. So here is the rule for the joint-groups Sudoku: the nine digits in a particular place in a 3 by 3 box contain not more than three distinct digits. It is easy to see that it means they contain exactly 3 distinct digits, each of them three times.
Here are two Sudoku puzzles from our paper. Each puzzle, when completed, forms a joint-groups Sudoku.
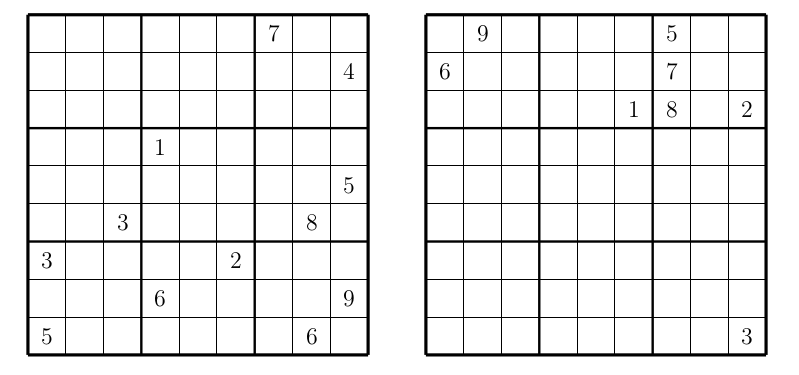
As you may know, I run PRIMES STEP, a local program where we do mathematical research with students in grades 6-9. Last academic year, we looked at the stable marriage problem and discovered its connection to Sudoku. Our paper The Stable Matching Problem and Sudoku (written jointly with Matvey Borodin, Eric Chen, Aidan Duncan, Boyan Litchev, Jiahe Liu, Veronika Moroz, Matthew Qian, Rohith Raghavan, Garima Rastogi, Michael Voigt) is now available at the arxiv.
Consider 3 men and 3 women who want to be married to each other in heterosexual couples. They rank each other without ties. The resulting 6 permutations of numbers 1, 2, and 3 that describe the six rankings are called the preference profile of this group of people. A matching is unstable if two people would be happier to run away together than to marry into the assigned couples. The two potential runaways are called a rogue couple. A matching is called stable if no rogue couple exists. The Gale-Shapley algorithm, invented by Gale and Shapley, finds a stable matching for any preference profile, implying that stable matching is always possible.
We discovered that preference profiles form a natural bijection with ways to place one digit into a Sudoku grid. So we wrote a paper describing the stable marriage, rogue couples, the Gale-Shapley algorithm, soulmates, and such in terms of Sudoku.
Oops, I forgot to explain who the soulmates are. We invented this term to describe two people who rank each other first. Though it is possible to have several stable matchings for the same preference profile if the soulmates exist, they must always be matched together.
We also invented a new Sudoku type, which I will explain next time.
I recently posted my puzzle designed for the MoMath meet-up.
What's in the Name?
Now it is time for the solution.
The solvers might recognize some sequences and numbers. For example, numbers 6, 28, and 496 are famous perfect numbers. Otherwise, the solvers are expected to Google the numbers and the pieces of the sequences with or without X. The best resource for finding the sequences is the Online Encyclopedia of Integer Sequence.
The first “AHA!” happens when the solvers notice that the sequences’ names are in alphabetical order. The order serves as a confirmation of the correctness of the names. It also helps in figuring out the rest of the sequences’ names. The alphabetical order in such types of puzzles hints that the real order is hidden somewhere else. It also emphasizes that the names might be important. The sequences names in order are:
The second “AHA!” moment happens when the solvers realize that the Xs all have different indices. The indices serve as the final order, which in this case is the following:
The third “AHA!” moment happens when the solvers realize that the number of terms is different in different sequences. It would have been easy to make the number of terms the same. This means that the number of terms has some significance. In fact, the number of terms in each sequence matches the length of the name of the sequence. The solvers then can pick the letter from each of the names corresponding to X. When placed in order, the answer reads: NUMBERS.
The answer is related to the puzzle in two ways:
The advantage of this puzzle for zoomed group events is that the big part of the job — figuring out the sequences — is parallelizable. Additionally, it has three “AHA!” moments, which means different people can contribute to a breakthrough. The puzzle also has some redundancy in it:
How can a square be square-free? In order for square-freeness to be interesting, it must be, and is, defined in terms of divisibility by non-trivial squares. So to create this particular mathematical oxymoron, one just needs a trivial square, namely 1.
I collect exciting properties of integers on my Number Gossip website. Did you know that forty is the only number whose letters appear in alphabetical order when written in English? Or that the largest amount of money one can have in US coins without being able to make change for a dollar is 119 cents?
Recently I wrote about a weird occasion that motivated me to search for new properties. Here is a sample of some amusing new updates.
This is the puzzle I designed for yesterday's event at the Museum of Mathematics. This puzzle is without instructions — figuring out what needs to be done is part of the fun. Solvers are allowed to use the Internet and any available tools. The answer to this puzzle is a word.
I've been too busy lately, so I stopped checking my Number Gossip website. Luckily, my website has fans. So one of them, Neil, notified me that my website was hijacked, and instead of describing properties of numbers, was selling steroids. I emailed Dreamhost, my hosting provider. They requested proof that I owned the domain. Why didn't they request proof from the people selling steroids? Or were they selling steroids themselves?
I fixed my steroid issue and since I was thinking about it anyway, I decided to update Number Gossip. I ended up spending tons of time on it — I had ten years of emails with suggestions for new properties, and I went through all of them and added the interesting ones. For example, Joshua Gray emailed me a cute property of 1331 mentioned on Wikipedia: 1331 was said to be the only cube of the form x2 + x − 1. I didn't see how to prove it, so I posted it as a question on mathoverflow. It turns out that 1331 is actually not the only cube of this form. There are three of them: −1 (for x = 0 or −1), 1 (for x = 1 or −2), and 1331 (for x = 36 or −37). So 1331 is the only non-trivial cube with this property. I had to fix Wikipedia. By the way, did you notice a symmetry? Plugging in x and −x − 1 into the quadratic produces the same value.
After processing all the emails related to Number Gossip, I got excited, so I continued working on it and added tons of new unique properties. Some of them I invented myself, some more were inspired by sequences in the OEIS database. I now have a collection of my new favorite unique properties, which I will post soon.
This is the sequence of numbers n such that 3 times the reversal of n plus 1 is the number itself. In other words, n = 3*reversal(n)+1. For example, 742 = 3*247+1. In fact, 742 is the smallest number with this property. How does this sequence continue, and why?
I recently published Sergei Bernstein's awesome Star Battle called Swiss Cheese. Another lovely Star Battle from him is called Hooks. You can play it online at puzz.link.
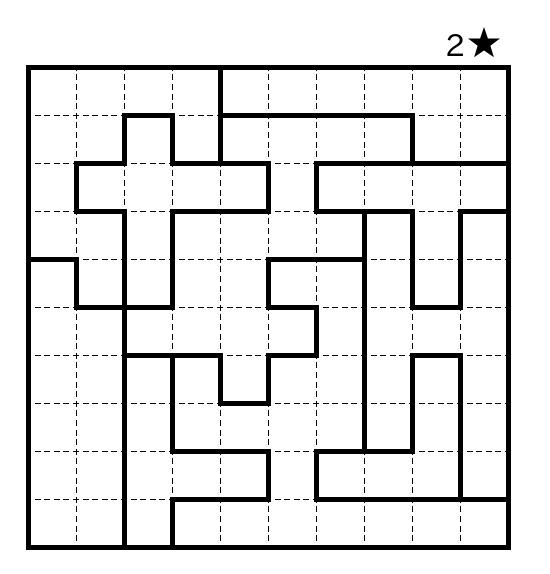
Star Battle is one of my favorite puzzle types. The rules are simple: put two stars in each row, column, and bold region (one star per cell). In addition, stars cannot be neighbors, even diagonally.
My son, Sergei Bernstein, recently designed a Star Battle with a beautiful solve path. This is my favorite Star Battle so far. I like its title too: Swiss Cheese.
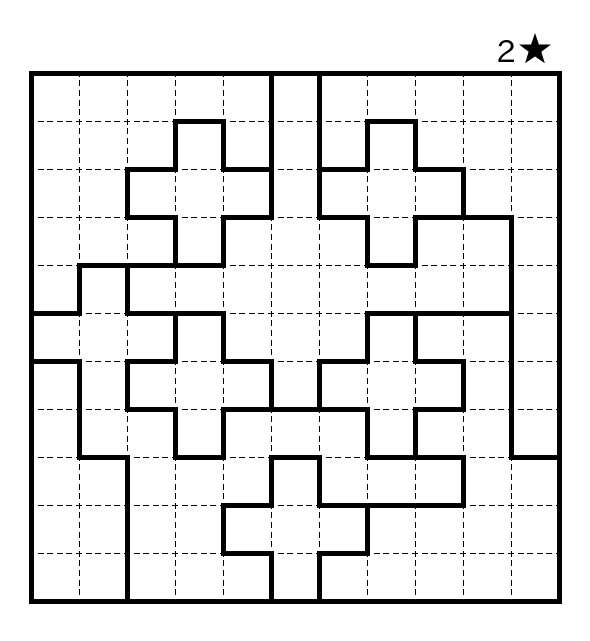
You can also solve it at the puzz.link Star Battle player.
A familect is a portmanteau word formed by squashing together two words: family and dialect. It means words that a family uses that are not a part of a standard vocabulary. This story is about two words that my son Sergei invented, and twenty years later, my family still uses them.
As you might know, I was married three times, and I have two sons, from two different fathers. These fathers were also married several times and had other children. My two sons are half-brothers, and they also have half-siblings through their fathers. Thus a half-sister of a half-brother became a quarter-sister. Inventing this term was quite logical for a son of two mathematicians.
As you can imagine, our family tree is complicated. One day Sergei pointed out that our tree doesn't look like a standard tree and called it a family bush.
A problem from the 2021 Moscow Math Olympiad went viral on Russian math channels. The author is Dmitry Krekov.
Problem. Does there exist a number A so that for any natural number n, there exists a square of a natural number that differs from the ceiling of An by 2?
Yesterday I stumbled upon a picture of John Conway I completely forgot I had: it was saved in a wrong folder. The photo was taken at the MOVES conference in 2015. There is a third person in the original shot, but I do not remember her. I decided to cut her out as I didn't know how to contact her for permission to post this photo.

Konstantin Knop, the world's top authority on coin-weighing puzzles, suggested the following problem for the 2019 Russian Math Olympiad.
Puzzle. Eight out of sixteen coins are heavier than the rest and weigh 11 grams each. The other eight coins weigh 10 grams each. We do not know which coin is which, but one coin is conspicuously marked as an "Anniversary" coin. Can you figure out whether the Anniversary coin is heavier or lighter using a balance scale at most three times?
Found the following cute puzzle on Facebook.
Puzzle. Discover the rule governing the following sequence to find the next term of the sequence: 8, 3, 4, 9, 3, 9, 8, 2, 4, 3.
This is one of my favorite problems given at the 2017 Moscow Olympiad to grades 6 and 7. It was suggested by one of my favorite problem writers: Alexander Shapovalov.
Problem. We are given eight unit cubes. The third of the total number of their faces are blue, and the rest are red. We build a large cube out of these cubes so that exactly the third of the unit cube's visible faces are red. Prove that you can use these cubes to build a large cube whose faces are entirely red.
For the last year, I've been obsessed with Penney's game. In this game, Alice picks a string of coin tosses, say HHH for three heads. After that, Bob picks his string of tosses of the same lengths, say HTH. Then they toss a fair coin. The person whose string shows up first wins. For example, if the tosses are THTTHHH, then Alice wins after the seventh toss. For these particular choices, Bob wins with probability 3/5.
With my PRIMES student, Sean Li, we looked at this game and asked a different question. Suppose Alice picks a pattern of three tosses in a row that are the same. Suppose after that, Bob chooses a pattern of three alternating tosses. Then they toss a fair coin. Alice is hoping for HHH or TTT, while Bob is hoping for HTH or THT. The person whose pattern shows up first wins. For example, if the tosses are THTTHHH, then Bob wins after the third toss. For these particular choices, Bob wins with probability 1/2.
In this example, what actually happens. We assume that the group of two elements acts on the alphabet of two letters. The group's non-identity element swaps letters H and T. We assume that two strings are equivalent if they belong to the same equivalency class under the group action. We call such an equivalency class a pattern.
In the new game we invented, we have an alphabet of any size and any group acting on the alphabet. Then Alice and Bob pick their patterns. After that, they play the Penney's game on these patterns. The answers to all the relevant questions are in our paper, The Penney's Game with Group Action, posted at the math.CO arxiv 2009.06080.
I wrote a paper Confirming the Labels of Coins in One Weighing together with my PRIMES STEP students Isha Agarwal, Paul Braverman, Patrick Chen, William Du, Kaylee Ji, Akhil Kammila, Shane Lee, Alicia Li, Anish Mudide, Jeffrey Shi, Maya Smith, and Isabel Tu. The paper is available at math.HO arxiv:2006.16797. Below my students describe what happens in the paper in their own words.
Tragedy has struck in an iCOINic land known as COINnecticut. One day, while everyone was minding their own business, the vault door of the bank was found to have been forcefully opened. COINcerns spread amongst the COINmoners that someone had tampered with their n sacred COINtainers of coins! The COINtainers are labeled with the integers 1 through n, which usually describe the weight of each of the countless coins inside that corresponding COINtainer. For example, the COINtainer labeled 1 should only COINtain coins that weigh 1 gram, the COINtainer labeled 2 should only COINtain coins that weigh 2 gram, and so on, you get the COINcept.
The acCOINtants COINclude that someone may have switched around the labels on the COINtainers. To resolve this COINplication, aka to check if the labels have been tampered with, they bought a balance scale for a microsCOINpic amount of money. However, they can only use the scale to COINduct one weighing as the angry COINmoners are impatient and wish to withdraw their money ASAP.
The COINfused acCOINtants COINvinced 11 COINspicuous students from Boston's COINmunity to help them. With their COINbined efforts, they COINcluded that indeed, no matter how many COINtainers there are, their labels can be COINfirmed as correct or incorrect with just one weighing! Unfortunately, sometimes, such a weighing requires the use of many coins or coins with a large COINbined weight, which could potentially break the scale. Seeing this COINundrum, the students wished to be eCOINomical and find the least amount of coins or weight they need to place on the scale.
The acCOINtants and the 11 students COINtinued examining the nature of these weighings and discovered patterns that occur within them. They COINfined their research to special weighings they called downhill. They COINfirmed the effectiveness of such weighings to solve the problem at hand. The students estimated the weight and the number of coins, thus COINpleting their task.
My PRIMES STEP students invented several variations of Penney's game. We posted a paper about these new games at math.HO arxiv:2006.13002.
In Penney's game, Alice selects a string of coin-flip outcomes of length n. Then Bob selects another string of outcomes of the same length. For example, Alice chooses HHT, and Bob chooses THH. Then a fair coin is tossed until Alice's or Bob's string appears. The player whose string appears first wins. In our example, Bob has a greater probability of winning, namely, 3/4. If the first two flips are HH, then Alice wins; otherwise, Bob wins.
The reader can check that HHT beats HTT with 2 to 1 odds. Thus, the game contains a non-transitive cycle it is famous for: THH beats HHT beats HTT beats TTH beats THH.
I already wrote about the No-Flippancy game that my students invented. It starts with Alice and Bob choosing different strings of tosses of the same length.
However, in the No-Flippancy game, they don't flip a coin but select a flip outcome deterministically according to the following rule: Let i ≤ n be the maximal length of a suffix in the sequence of "flips" that coincides with a prefix of the current player's string. The player then selects the element of their string with index i + 1 as the next "flip." Alice goes first, and whoever's string appears first in the sequence of choices wins.
My favorite game among the invented games is the Blended game, which mixes the No-Flippancy game and Penney's game.
In the game, they sometimes flip a coin and sometimes don't. Alice and Bob choose their strings as in Penney's game and the No-Flippancy game. Before each coin flip, they decide what they want by the rule of the No-Flippancy game above. If they want the same outcome, they get it without flipping a coin. If they want different outcomes, they flip a coin. Whoever's string appears first in the sequence of `flips' wins.
For example, suppose Alice selects HHT, and Bob selects THH. Then Alice wants H and Bob wants T, so they flip a coin. If the flip is T, then they both want Hs, and Bob wins. If the first flip is H, they want different things again. I leave it to the reader to see that Bob wins with probability 3/4. For this particular choice of strings, the odds are the same as in Penney's game, but they are not always the same.
This game has a lot of interesting properties. For example, similar to Penney's game, it has a non-transitive cycle of choices. Surprisingly, the cycle is of length 6: THH beats HHT beats THT beats HTT beats TTH beast HTH beat THH.
I spend a lot of time working on my blog, and I used to think it would be nice to get some money out of it.
Years ago I got two emails from different ad agencies at the same time. They wanted to place ads at particular essays for $50 a year. I decided to give them a try.
My first correspondent wanted a link on my "Does Alcohol in Teens Lead to Adult Woes?" essay, connecting to a website offering help to alcoholics. I agreed. But when I read the actual text, I couldn't stop laughing. The text they wanted to use was, "Many studies have already claimed that teenage alcoholism could lead to more problems later in life." How ironic! This ad would follow my essay explaining that one of the studies is completely bogus. I rejected them.
The second agency wanted an ad accompanying the essay "Subtraction Problems, Russian Style." I placed it. They wrote to me (and I reproduce it with all of their errors intact):
I really appreciate your efforts on this. As I checked the text link, I have seen that the text link has been label as "Sponsor ad". Kindly omit or delete the word "Sponor ad:" or you may changed it to "Recommended site or Relevant Site" but I would love to prefer the text link be seen as natural meaning no labeled inserted on it.
They wanted me to pretend that I recommend their product. I was naive enough to think that I was selling space on my page, but what they really wanted was for me to lie that I like their product.
Before this experiment, I hoped to find some honest ads for my blog. After this experiment, I realized how much stupidity and falsehood are involved. Since then, I ignore all offers of ads that come my way. That's why my blog is ad-free.
My STEP students invented a coin-flipping game that doesn't require a coin. It is called The No-Flippancy Game.
Alice and Bob choose distinct strings of length n consisting of the letters H (for heads) and T (for tails). The two players alternate selecting the outcome of the next "flip" to add to the sequence by the rule below.
The "flip" rule: Let i < n be the maximal length of a suffix of the sequence of chosen outcomes that coincides with a prefix of the current player’s string. The player then selects the element of their string with index i + 1 as the next term in the sequence.
Alice goes first, and whoever's string appears first in the sequence of choices wins. In layman terms, the game rules mean that the players are not strategizing, but rather greedily finishing their strings.
Suppose n = 2 and Alice chose HH. If Bob chooses HT, then Bob wins. Alice has to choose H for the first flip. Then Bob chooses T and wins. On the other hand, if Bob chooses TT for his string, the game becomes infinite. On her turn, Alice always chooses H, while on his turn Bob always chooses T. The game outcome is an alternating string HTHTHT... and no one wins.
Suppose n = 4, Alice chooses HHTT, and Bob chooses THHH. The game proceeds as HTHHTHHH, at which point Bob wins.
This game is very interesting. The outcome depends on how Alice's and Bob's chosen strings overlap with each other. We wrote a paper about this game, which is available at math.CO arXiv:2006.09588.
Every year I write about latest MIT Mystery Hunt puzzles that might be appealing to mathematicians. Before diving into mathy puzzles, I would like to mention two special ones:
Unfortunately math wasn't prominent this year:
On the other hand, Nikoli-type puzzles were represented very well:
Some computer sciency puzzles:
Cryptography:
A couple of puzzles with the mathy side hidden:
The academic year is over and my junior PRIMES STEP group finished their paper about a classification of magic SET squares. A magic SET square is a 3 by 3 square of SET cards such that each row, column, and diagonal is a set. See an example below. The paper is posted at the arXiv:2006.04764.
In addition to classifying the magic SET squares, my students invented the game of SET tic-tac-toe. It is played on nine cards that form a magic SET square. Two players take turns picking a card from the square. The first player who has a set wins.
One might think that this game is the same as tic-tac-toe, as a player wins as soon at they have cards from the same row, column, or diagonal. But if you build a magic SET square, you might notices that each magic SET square contains 12 sets. In addition to rows, columns, and diagonals, there are sets that form broken diagonals. The picture below shows all the sets in a magic SET square.
There are more ways to win in this game than in a regular tic-tac-toe game. My students proved that ties are impossible in this game. They also showed, that, if played correctly, the first player always wins.
You probably heard in the news that more men are dying from coronavirus than women. But not in Massachusetts. Here the proportion of women is about 52 percent. Why is this the case? Being a woman, should I be worried that I live in Massachusetts?
We know that coronavirus strikes older people harder than younger ones. Thus, we should take age into account. In the US more boys are born than girls. By the age of 40 the ratio evens out. Starting from 40 there are more women than men. With each next age group, the disparity increases. According to a recent US population report and for ages 85 and over there are about 4.22 million women versus 2.33 men: the proportion is almost 2 to 1.
As the coronavirus targets older people, were it gender-neutral, we would have had way more female deaths than male. This is not the case. So it hits males harder than females. But why are the ratios of female to male deaths different for different countries and states?
One simple explanation is that this is related to life expectancy and the age of the population. The older the population, the bigger the percentage of females. Which in turn increases the proportion of female deaths.
It could also be that Massachusetts has good health care making the average age of dying patients older than the average age for the country. This in turn will increase the proportion of females dying from coronavirus. No, I am not worried about living in Massachusetts.
I grew up in the USSR, where I was clueless about the race issues in the US. I have now lived in the US for 30 years, and still feel that there are many things about race that I do not understand. As a result, I am afraid to speak about it. I am worried that I'll say something wrong. Recent events have encouraged me to say something. This is my first piece about race.
I came back to mathematics 10 year ago and started working at MIT. I love it. With some exceptions.
Many mathematicians are introverts or snobs or gender-biased. They are not usually friendly. I often walk down a corridor and people who are coming towards don't notice me. If I say hello, they might not even reply or raise their eyes. It could be they are thinking about their next great theorem and do not notice me. It could be that I am not faculty and therefore do not deserve their attention. It could be that as a women I am not worth of their hello.
Soon after I started working at MIT, I was reminded of one of the reasons I left academia. It was this unfriendliness. But this time was different. First, I had grown a thicker skin. Second, I was working within a group. People who were working with me were nice to me. It was enough and so I stayed.
With time I adopted the same style: passing people without saying `Hello.' Mostly I got tired of people not replying to my hello.
One day I was passing this man who, as had happened many times before, purposefully didn't look at me. I thought my usual thought: another introverted/snobbish/gender-biased mathematician. Then I suddenly stopped in my tracks. My logic was wrong. This guy was Black. The unfriendliness of mathematicians is surely way worse for him than for me. It could be that he is looking at the floor for the same reason I do it: he is afraid that people will ignore his greeting. I failed to think about race deep enough before this realization. What happened next should have happened years earlier.
I took the initiative and the next couple of times I saw him, I said hello. This was all it took—two hellos—to change the whole feeling between us. The guy has a great smile.
It was reported last week that that 37 NYPD members died of covid-19. I assume that they were way below 65. It is known that the coronovirus death rate for people below 65 is a quarter of the total death rate. That means, 37 people in NYPD correspond to at least 150 people in general. Assuming that the mortality rate of coronavirus is 1 percent, the number of infected NYPD members a month ago was 15000.
By now, it could be that more than half of NYPD was infected.
NYPD members have to communicate with people a lot due to the nature of their work. That means they are more prone to being infected. At the same time, they transmit more than people in many other professions.
I can conclude, that about half of the people that are high transmitters in NY have antibodies by now. Assuming they are immune, the covid transmission rate in NY has to be down.
Assuming the immunity stays with people for a while, the second wave in NY can't be as bad as the first one.
Suppose we want to pack a unit square with non-overlapping rectangles that have sides parallel to the axes. The catch is that the lower left corners of all the rectangles are given. By the way, such rectangles are called anchored. Now, given some points in the unit square, aka the lower left corners, we want to find anchored rectangles with the maximum total area.
When the given points are close to the right upper corner of the square, the total area is small. When a single point is in the bottom left corner of the square, we can cover the whole square. The problem becomes more interesting if we add one extra assumption: one of the given points has to be the bottom left corner of the square. In the 1960's, it was conjectured by Allen Freedman that any set of points has an anchored rectangle packing with the area of at least one half. The problem is quite resistant. In 2011, Dumitrescu and Tóth showed that every set of points has a packing of area at least 0.09, which was the first constant bound found, and is the best bound currently known.
I gave this problem to my PRIMES student Vincent Bian. He wrote a paper, Special Configurations in Anchored Rectangle Packings, that is now available at the arxiv. When you look at this problem you see that the number of ways to pack depends on the relative coordinates of the points. That means you can view the points as a permutation. Vincent showed that the conjecture is true for several different configurations of points: increasing, decreasing, mountain, split layer, cliff, and sparse decreasing permutations.
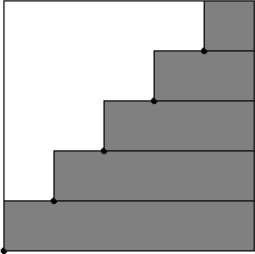
An increasing permutation is easy. There are two natural ways to pack the rectangles. One way, when rectangles are horizontal and each rectangle reaches to the right side of the square (see picture above). Another way, when rectangles are vertical. When you take the union of both cases, the square is completely covered, which means at least one of the cases covers at least half of the square. The worst case scenario, that is, the case when the maximum possible area is the smallest is when your points are placed equidistantly on the diagonal.
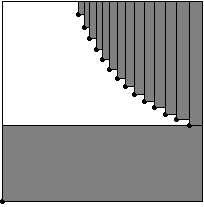
Other cases are more difficult. For example, Vincent showed that for a decreasing permutation with n points, the worst case scenario is when the points are arranged equidistantly on a hyperbola xy = (1-1/n)n. The picture shows the configuration for 15 points. The total area is more than one half.
(I wrote this piece for La Recherche. It was translated into French by Philippe PAJOT. You can find this piece and pieces by others at John Horton Conway: a magician of maths disappears.)
Unlike many other mathematicians I know, John Conway cared a lot about the way he presented things. For example, in the puzzle he invented—known as Conway's Wizards—the wizards had to be riding on a bus. Why was the bus so important? You see, the numbers in the puzzle were related to the age of one of the wizards, the number of the bus, and the number of the wizard's children. It was important to John that the readers be able to use a convenient notation a, b and c for these numbers and remember which number is which.
When I give my lecture on integers and sequences, I show my students a list of different famous sequences. The first question from the audience is almost always: "What are the Evil Numbers?" As you can guess the name for this sequence was invented by John Conway. This name was invented together with the name of another sequence which is called Odious Numbers. These two sequences are complementary in the same sense as even and odd numbers are complementary: every natural number is either evil or odious. The names are good, not only because they attract, but also because they help remember what the sequences are. Evil numbers are numbers with an even number of ones in their binary representation. I assume that you can interpolate what the odious numbers are.
When he was lecturing, John used all sorts of tricks to emphasize important points: From time to time I saw him shouting or throwing his shoes. Once I remember him staring at his statement written on the blackboard for a really long time. My neighbor in the lecture hall got uncomfortable. He assumed that John, who was at that time way over 70, was blanking out and had forgotten what he wanted to say. I calmed my neighbor down. It was my fourth time listening to the same lecture, including the same pause. John Conway didn't forget.
The picture was taken on December 21 of 2019 at Parker Life care facility right before dinner.

Every year I review MIT mystery hunt from a mathematician's point of view. I am way behind. The year is 2020, but I still didn't post my review of 2019 hunt. Here we go.
Many puzzles in 2019 used two data sets. Here is the recipe for constructing such a puzzle. Pick two of your favorite topics: Star Trek and ice cream flavors. Remember that Deanna Troi loves chocolate sundae. Incorporate Deanna Troi into your puzzle to justify the use of two data sets.
On one hand, two data sets guarantee that the puzzle is new and fresh. On the other hand, often the connection between two topics was forced. Not to mention that puzzle solving dynamic is suboptimal. For example, you start working on a puzzle because you recognize Star Trek. But then you have to deal with ice cream which you hate. Nonetheless, you are already invested in the puzzle so you finish it, enjoying only one half of it.
Overall, it was a great hunt. But the reason I love the MIT mystery hunt is because there are a lot of advanced sciency puzzles that can only appear there. For example, there was a puzzle on Feynman diagrams, or on characters of representations. This year only one puzzle, Deeply Confused, felt like AHA, this is the MIT Mystery hunt.
Before discussing mathy puzzles I have to mention that my team laughed at Uncommon Bonds.
I will group the puzzles into categories, where the categories are obvious.
Mathy puzzles.
Here are some logic puzzles, in a sense that Sudoku is a logic puzzle.
Now we have logic puzzles or another type, where you need to draw a grid. These are puzzles of the type: Who lives in the White House?
Now we have logic puzzles or yet another type, where you need to figure out which statements are true and which are false.
Now some cryptography.
And some programming.
Miscellaneous.
Every day I check coronavirus numbers in the US. Right now the number of deaths is 288 and the number of recovered is 171. More people died than recovered. If you are scared about the mortality rate, I can calm you and myself down: our government is incompetent—the testing wasn't happening—that means the numbers do not show people who had mild symptoms and recovered. The real number of recovered people should be much higher.
Scientists estimated the mortality rate of coronavirus as being between 1 and 3.5 percent. Also, they say that it usually takes three weeks to die. That means three weeks ago the number of infected people in the US was between 8,000 and 29,000. The official number of cases three weeks ago was 68. I am panicking again—our government is incompetent—three weeks ago they detected between 0.25 and 1 percent of coronavirus cases. If this trend continues, then the official 19,383 infected people as of today means, in reality, somewhere between 2 million and 8 million infected people.
I can calm you and myself down: the testing picked up pace. This means, the ratio of detected cases should be more than 1 percent today. Probably the number of infected people today in the US is much less than 8 million. I am not calm.
My former student, Dai Yang, sent me the following cute puzzle:
Puzzle. You are playing a game with the Devil. There are n coins in a line, each showing either H (heads) or T (tails). Whenever the rightmost coin is H, you decide its new orientation and move it to the leftmost position. Whenever the rightmost coin is T, the Devil decides its new orientation and moves it to the leftmost position. This process repeats until all coins face the same way, at which point you win. What's the winning strategy?
My friend Zeb, aka Zarathustra Brady, invented a new game that uses chess pieces and a chessboard. Before the game, the players put all chess pieces on white squares of the board: white pieces are placed in odd-numbered rows and black pieces are in even-numbered rows. At the beginning all white squares are occupied and all black squares are empty. As usual white starts.
On your turn, you can move your piece from any square to any empty square as long as the number of enemy neighbors doesn't decrease. The neighbors are defined as sharing a side of a square. Before the game starts each piece has zero enemy neighbors and each empty square has at least one white and one black neighbor. That means that on the first turn the white piece you move will increase the number of neighbors from zero to something. As usual, the player who doesn't have a move loses.
As you can immediately see, that number of pairs of enemy neighbors is not decreasing through the game. I tried to play this game making a move which minimizes the increase of the pairs of neighbors. I lost, twice. I wonder if there is a simple strategy that is helpful.
It is important that this game is played with chess pieces in order to confuse your friends who pass by. You can see how much time it takes them to figure out that this game is not chess, but rather a Chessnot. Or you can enjoy yourself when they start giving you chess advice before realizing that this is not chess, but rather a Chessnot.
I heard this puzzle many years ago, and do not remember the origins of it. The version below is from Peter Winkler's paper Seven Puzzles You Think You Must Not Have Heard Correctly.
Puzzle. Jan and Maria have fallen in love (via the internet) and Jan wishes to mail her a ring. Unfortunately, they live in the country of Kleptopia where anything sent through the mail will be stolen unless it is enclosed in a padlocked box. Jan and Maria each have plenty of padlocks, but none to which the other has a key. How can Jan get the ring safely into Maria's hands?
I don't know whether this puzzle appeared before the Diffie-Hellman key exchange was invented, but I am sure that one of them inspired the other. The official solution is that Jan sends Maria a box with the ring in it and one of his padlocks on it. Upon receipt Maria affixes her own padlock to the box and mails it back with both padlocks on it. When Jan gets it, he removes his padlock and sends the box back, locked only with Maria's padlock. As Maria has her own key, she can now open it.
My students suggested many other solutions. I wonder if some of them can be translated to cryptography.
Now that we've looked at the Padlock Puzzle, let's talk about cryptography. I have an imaginary student named Charlie who doesn't know the Diffie-Hellman key exchange. Charlie decided that he can adapt the padlock puzzle to help Alice send a secret message to Bob. Here's what Charlie suggests:
Suppose the message is M. Alice converts it to binary. Then she creates a random binary key A and XORs it with M. She sends the result, M XOR A, to Bob. Then Bob creates his own random key B and XORs it with what he receives and sends the result, M XOR A XOR B, back to Alice. Alice XORs the result with her key to get M XOR A XOR B XOR A = M XOR B and sends it to Bob. Bob XORs it with his key to decipher the message.
Each sent message is equivalent to a random string. Intercepting it is not useful to an evil eavesdropper. The scheme is perfect. Or is it?
Here is a logic puzzle.
Puzzle. You are visiting an island where all people know each other. The islanders are of two types: truth-tellers who always tell the truth and liars who always lie. You meet three islanders—Alice, Bob, and Charlie—and ask each of them, "Of the two other islanders here, how many are truth-tellers?" Alice replies, "Zero." Bob replies, "One." What will Charlie's reply be?
The solution proceeds as follows. Suppose Alice is a truth-teller. Then Bob and Charlie are liars. In this situation Bob's statement is true, which is a contradiction. Hence, Alice is a liar. It follows, that there is at least one truth-teller between Bob and Charlie. Suppose Bob is a liar. Then the statement that there is one truth-teller between Alice and Charlie is wrong. It follows that Charlie is a liar. We have a contradiction again. Thus, Alice is a liar and Bob is a truth-teller. From Bob's statement, we know that Charlie must be a truth-teller. That means, Charlie says "One."
But here is another solution suggested by my students that uses meta considerations. A truth-teller has only one possibility for the answer, while a liar can choose between any numbers that are not true. Even if we assume that the answer is only one of three numbers—0, 1, or 2—then the liar still has two options for the answer. If Charlie is a liar, there can't be a unique answer to this puzzle. Thus, the puzzle question implies that Charlie is a truth-teller. It follows that Alice must be lying and Bob must be telling the truth. And the answer is the same: Charlie says, "One."
You might have noticed that my blogging slowed down significantly in the last several months. I had mono: My brain was foggy, and I was tired all the time. Now I am feeling better, and I am writing again. What better way to get back to writing than to start with some jokes?
* * *
The wife of a math teacher threw him out from point A to point B.
* * *
At the job interview at Google.
—How did you hear about our company?
* * * (submitted by Sam Steingold)
50% of marriages end with divorce. The other 50% end with death.
* * *
People say that I am illogical. This is not so, though this is true.
* * *
Humanity invented the decimal system, because people have 10 fingers. And they invented 32-bit computers, because people have 32 teeth.
* * *
When a person tells me, "I was never vaccinated, and, as you can see, I am fine," I reply, "I also want to hear the opinion of those who were never vaccinated and died."
* * *
I will live forever. I have collected a lot of data over the years, and in all of the examples, it is always someone else who dies.
* * *
Just got my ticket to the Fibonacci convention! I hear this year is going to be as big as the last two years put together.
* * *
I am afraid to have children as one day I will have to help them with math.
This is my favorite puzzle in the last issue of the Emissary, proposed by Peter Winkler.
Puzzle. Alice and Bob each have 100 dollars and a biased coin that flips heads with probability 51%. At a signal, each begins flipping his or her coin once per minute, and betting 1 dollar (at even odds) on each flip. Alice bets on heads; poor Bob, on tails. As it happens, however, both eventually go broke. Who is more likely to have gone broke first?
Follow-up question: As above, but this time Alice and Bob are flipping the same coin (biased 51% toward heads). Again, assume both eventually go broke. Who is more likely to have gone broke first?
Puzzle. You got two envelopes with two distinct real numbers. You chose one of them and open it. After you see the number you are allowed to swap envelopes. You win if at the end you pick the larger number. Find a strategy that gives you a probability more than 1/2 of winning.
Another cute puzzle found on Facebook.
Puzzle. A teacher wrote four positive numbers on the board and invited his students to calculate the product of any two. The students calculated only five of six products and these are the results: 2, 3, 4, 5, 6. What is the last product? What are the original four numbers?
I found this puzzle on Facebook:
Puzzle. Solve this:
1+4 = 5,
2+5 = 12,
3+6 = 21,
5+8 = ?
97% will fail this test.
Staring at this I decided on my answer. Then I looked at the comments: they were divided between 34 and 45 and didn't contain the answer that initially came to my mind. The question to my readers is to explain the answers in the comments and suggest other ones. Can you guess what my answer was?
Puzzle. The length of the day today in Boston is the same as the length of the coming night tonight. What is the total length of both?
My friend Alice reminds me of me: she has two sons and she is never straight with her age. Or, maybe, she just isn't very good with numbers.
Once I visited her family for dinner and asked her point blank, "How old are you?" Here is the rest of the conversation:
Alice: I am two times older than my younger son was 5 years ago.
Bob: My mom is 12 times older than my older brother.
Carl: My younger brother always multiplies every number he mentions by 24.
Bob: My older brother is 30 years older than me.
Carl: My mom is 8 times older than me.
Alice: My older son always multiplies every number he mentions by 2.
How old is everyone?
Last year, when I read an application file of Wayne Zhao to PRIMES, I got very excited because he liked puzzles. And I've always wanted to have a project about puzzles. After Wayne was accepted to PRIMES we started working together. Wayne chose to focus on a variation of Sudoku called Sudo-Kurve.
We chose a particular shape of Sudo-Kurve for this project, which ended up being very rewarding. It is called Cube Sudo-Kurve. The Cube Sudo-Kurve consists of three square blocks. The gray bent lines indicate how rows and columns continue. For example, the first row of the top left block becomes the last column of the middle block and continues to the first row of the bottom right block. As usual each row, column, and square region has to have 9 distinct digits.
Wayne and I wrote a paper Mathematics of a Sudo-Kurve, which has been published at Recreational Mathematics Magazine.
A Cube Sudo-Kurve needs at least 8 clues to have a unique solution. Here we have a puzzle with 8 clues that we designed for our paper.
I've been invited to help with the Puzzle Column at the MSRI newsletter Emissary. We prepared six puzzles for the Fall 2018 issue.
I love the puzzles there. Number 2 is a mafia puzzle that I suggested. Number 6 is a fun variation on the hat puzzle I wrote a lot about. Here is puzzle Number 3.
Puzzle. Let A = {1,2,3,4,5} and let P be the set of all nonempty subsets of A. A function f from P to A is a "selector" function if f(B) is in B, and f(B union C) is either equal to f(B) or f(C). How many selector functions are there?

When I was in grade school, one of the teachers called me Cave Lioness. She hated my unruly hair, which reminded her of a lion's mane. This teacher was obviously very uninformed, for female lions do not have manes.
This name calling had the opposite to the desired effect. I became proud of my mane and didn't ever want to cut it. When I grew older, I opted for convenience and started to cut my hair short—sometimes very short.
Last year I was too busy for barbers, and my hair grew more than I intended. As it turned into a mane, I remembered the story of this nickname.
Once I was giving a math lecture and my phone, which I've never quite understood, was on the desk in front of me. Suddenly it rang. I didn't pick it up, as I proceeded with my lecture. The ringing stopped, while I was explaining a particularly interesting mathematical point. After a minute, my phone said, "I do not understand a word you are saying."
Detective Radstein is investigating a robbery. He apprehends three suspects: Anne, Bill, and Caroline. The detective knows that no one else could have participated in the robbery. During the interrogation the suspects make the following statements:
Detective Radstein also discovered that all three suspects are members of a club called The Halfsies. Every time they speak, they make two statements, one of which is a lie and the other one is true. Who committed the robbery?

I already wrote about my first experience crocheting hyperbolic surfaces. In my first surface I added two more stitches per current stitch. It took me hours to crochet the last row: the same hours it took me to crochet the rest.
For my next project, I reduced the ratio. The light blue thingy has ratio 3/2. I continued making my life simpler. The next project, the purple surface on the left, has ratio 4/3. The last project on the right has a ratio of 5/4 and is my favorite. Mostly because I am lazy and it was the fastest to make.
How much time will it take you to answer the following question?
Can the equation 29x + 30y + 31z = 366 be solved in natural numbers?
Happy 2019, the first 4 digit number to appear 6 times in the decimal expansion of Pi.
By the way, 2019 is the product of two primes 3 and 673. The sum of these two prime factors is a square.
This is not all that is interesting about factors of 2019. Every concatenation of these two prime factors is prime. Even more unusual, 2019 is the largest known composite number such that every concatenation of its prime factors is prime. [Oops, the last statement is wrong, Jan 3,2019]
Happy Happy-go-Lucky year, as 2019 is a Happy-go-Lucky number: the number that is both Happy and Lucky.
In case you are wondering, here is the definition of Happy numbers: One can take the sum of the squares of the digits of a number. Those numbers are Happy for which iterating this operation eventually leads to 1.
In case you are wondering, to build the Lucky number sequence, start with natural numbers. Delete every second number, leaving 1, 3, 5, 7, 9, 11, 13, 15, 17, 19, 21, …. The second number remaining is 3, so delete every third number, leaving 1, 3, 7, 9, 13, 15, 19, 21, …. The next number remaining is 7, so delete every 7th number, leaving 1, 3, 7, 9, 13, 15, 21, …. The next number remaining is 9, so delete every ninth number, etc.
Last revised December 2023